混合策略改进的麻雀优化算法

陈 俊,何 庆

(贵州大学 大数据与信息工程学院,贵阳 550025) (贵州大学 贵州省公共大数据重点实验室,贵阳 550025)

1 引 言

在过去的几年里,全局优化问题在数学,经济,工程实践中应用规模不断扩大.传统优化方法对于其中具有高维度,非线性,目标函数不可导,复杂的全局优化问题,很难在合理的时间内解决[1-3].受到生物系统的启发,国内外学者开始研究群智能优化算法.例如粒子群算法(PSO)[4]、蚁群优化算法(ACO)[5]、蝴蝶优化算法(BOA)[6]、差分进化算法(DE)[7]、布谷鸟算法(CS)[8]、鲸鱼优化算法(WOA)[9]、北极熊优化算法(PBO)[10]等.

受到麻雀觅食和反捕食行为的启发,麻雀优化算法(Sparrow Search Algorithm,SSA)[11]由薛建凯于2020年提出,该算法相比其它群智能优化算法,具有原理简单、灵活性好、易于实现等优点,从而被学者应用于各个领域中.目前麻雀优化算法已经成功的应用于多阈值图像分割[12],多目标优化问题[13],无人机航迹规划问题[14],但是麻雀优化算法同其它群智能算法一样,在求解接近全局最优时,仍然存在群体多样性下降、易陷入局部最优、求解精度不高等缺点.

针对SSA存在的问题,学者们相继对SSA进行了改进,譬如欧阳城添[15]等人提出了一种融合K-means的多策略改进麻雀搜索算法,通过K-means算法对初始种群进行聚类,加快种群之间的交流.引入正余弦搜索策略和自适应局部搜索方式,提高了收敛精度和寻优能力;吕鑫[16]等人提出一种混沌麻雀搜索优化算法,引入改进后的tent混沌序列初始化种群,其次引入高斯变异,加强局部搜索.汤安迪[14]等人提出混沌麻雀搜索算法,使用立方映射混沌算子[17],保证初始种群的均匀性;其次使用反向学习策略[18],正余弦算法[19]来增强种群的多样性;毛清华[20]等人提出了一种融合柯西变异和反向学习的改进麻雀算法,利用sin混沌序列初始化麻雀个体位置,其次引入自适应惯性权重,协调局部和全局搜索能力,最后融合反向学习和柯西变异算子进行变异扰动,增强跳出局部最优的能力.上述改进策略在一定程度上改善了SSA算法的性能,但是面对求解规模较大的函数优化问题上还需要更深入的研究.

综上而言,本文提出一种混合策略改进的麻雀搜索算法(Mixed strategy to improve Sparrow Search Algorithm,MI-SSA),首先引入佳点集法初始化麻雀个体位置,使得初始个体尽可能的遍历整个搜索空间.然后利用混合黄金正弦和莱维飞行策略以及t-分布扰动策略共同实现发现者位置更新,改善算法在迭代后期种群多样性的减少的缺陷.最后通过动态调整侦察者数量,在此来保证种群的多样性,提高算法跳出局部最优的能力.将本文所提算法在14个经典基准函数,Wilcoxon秩和检验以及CEC2014函数上进行数值实验,验证本文所提算法的鲁棒性,有效性以及优越性.

2 麻雀优化算法

麻雀优化算法是一种新型群智能优化算法,该算法主要分为3种成分,分别是发现者、加入者和侦察者.同时这3种成分对应3种行为,首先具有较好适应度的发现者寻找食物,以获取食物来源,一般占到种群的10%～20%.其次是加入者,加入者紧跟随发现者觅食,以争取食物,发现者和加入者之间可相互转换,该行为称为夺取机制.最后从种群中随机选取10%～20%的麻雀作为侦察者进行监视,当扑食者出现时以便麻雀种群及时做出应对反映.

其中发现者位置更新如下:

(1)

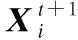
加入者位置更新如下:

(2)

最后,麻雀优化算法的侦察者位置更新如下:

(3)

3 混合策略改进的麻雀优化算法

3.1 佳点集的种群初始化

优秀的初始化种群策略能够使种群个体更均匀的遍历整个搜索空间,增强种群的多样性,为算法的全局搜索奠定了基础.在初始化种群阶段,SSA在初始化种群的过程中容易受到随机性的干扰,发生聚集现象.本文引入佳点集初始化方法,有效提高算法在解空间上的遍历能力.

佳点集最初由华罗庚[21]等人提出,根据文献[22]佳点集产生原理得到点分布序列,在将初始化序列映射到解空间.该方法的构造与空间维数无关,能够很好地适应高维问题,且取点稳定.理论上,使用佳点集法生成的点的偏差远小于随机选择的点.通过对佳点集法和随机法生成二维初始种群进行对比,如图1所示.在相同的取点个数下,使用佳点集初始化方法的个体比随机初始化方法的个体更加均匀.

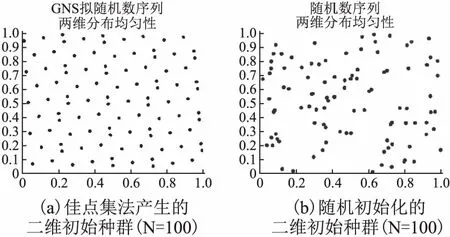
图1 二维初始种群分布图Fig.1 2-D initial population distribution

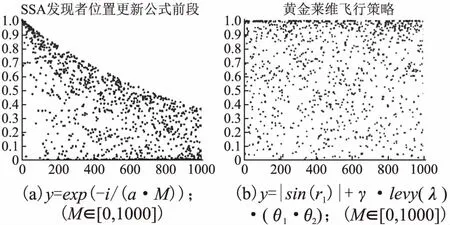
3.2 黄金莱维飞行策略

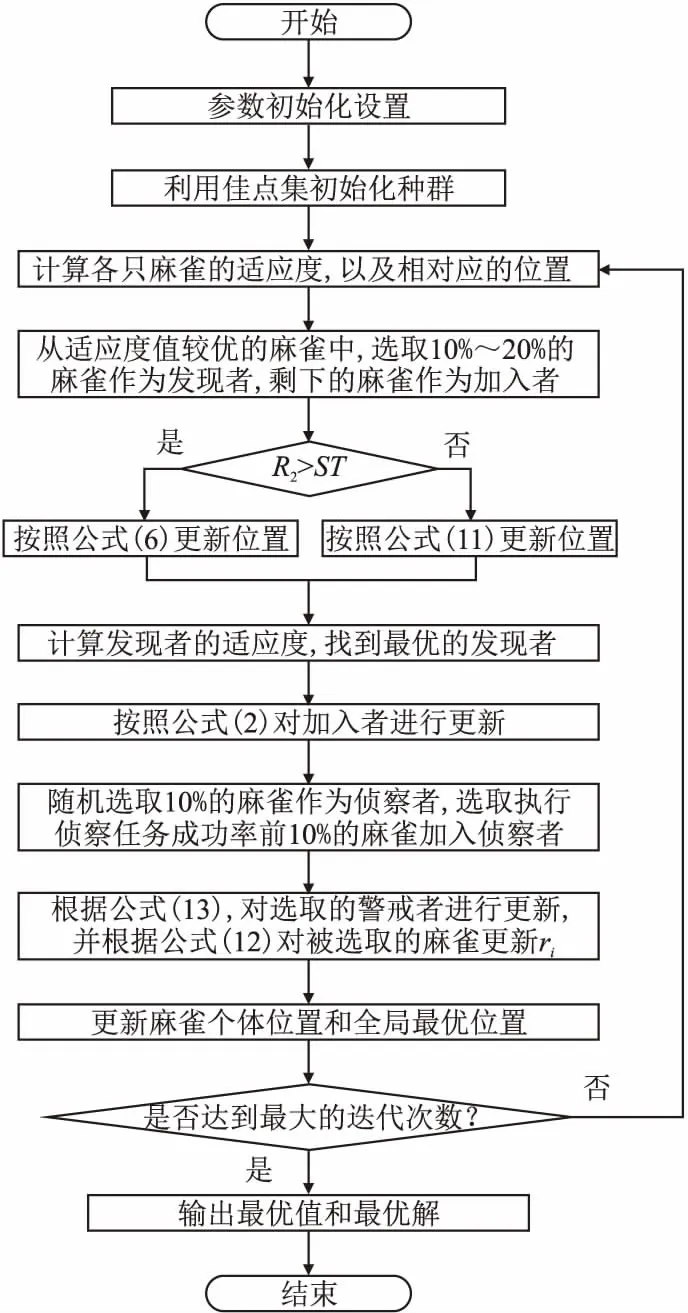
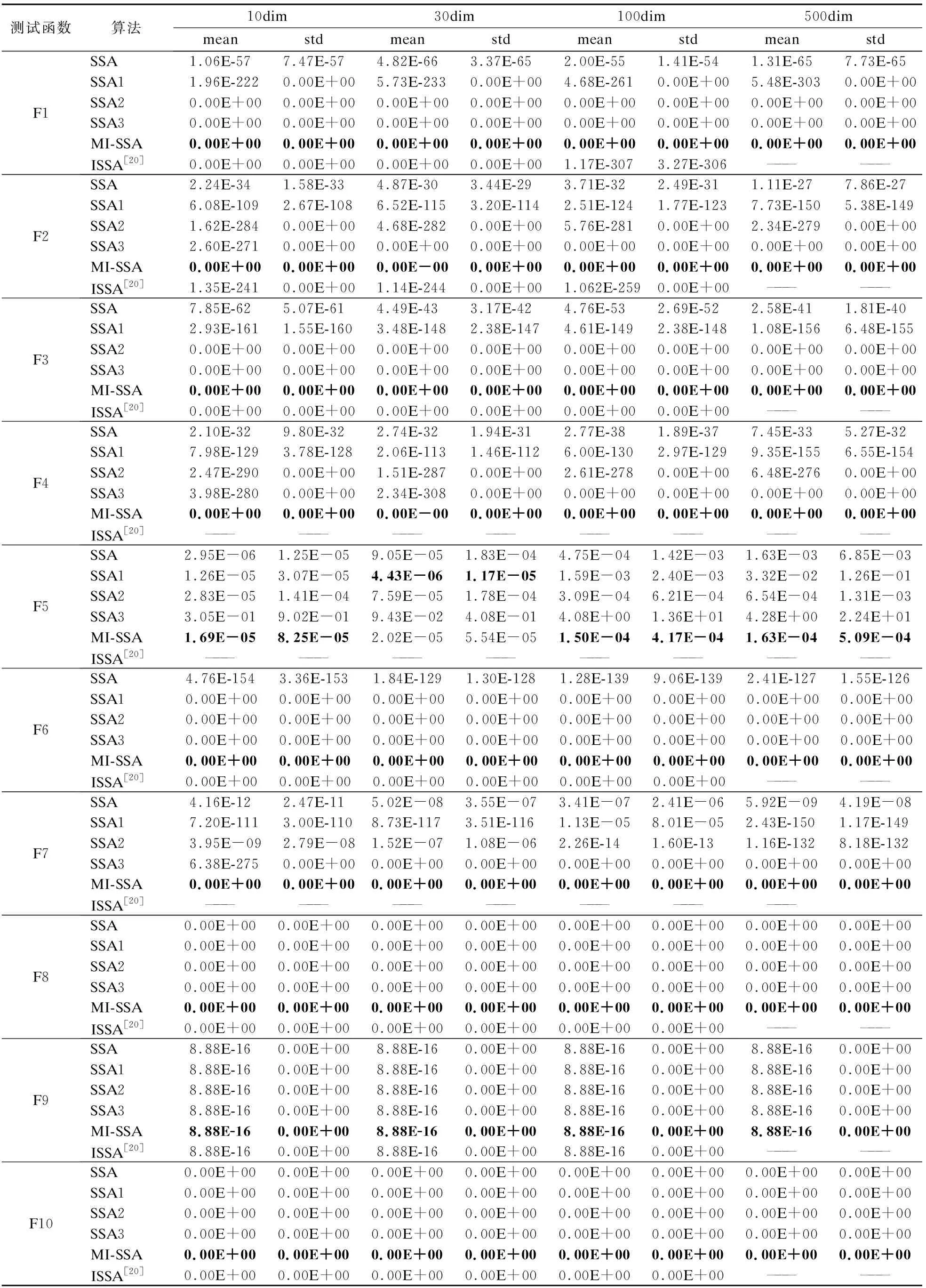
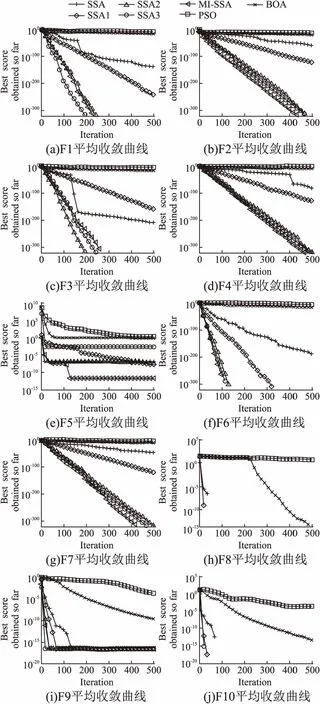
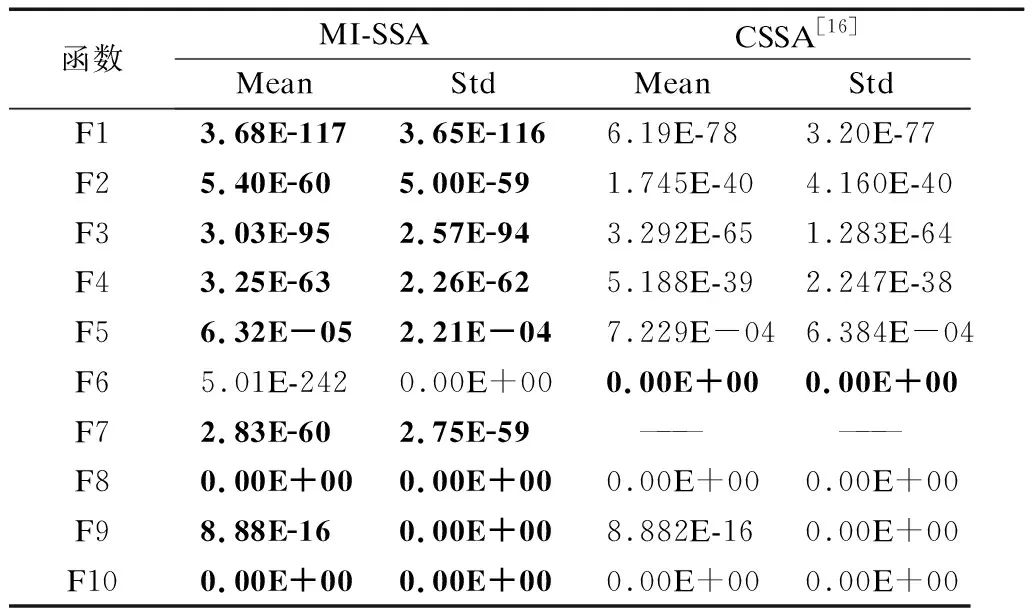
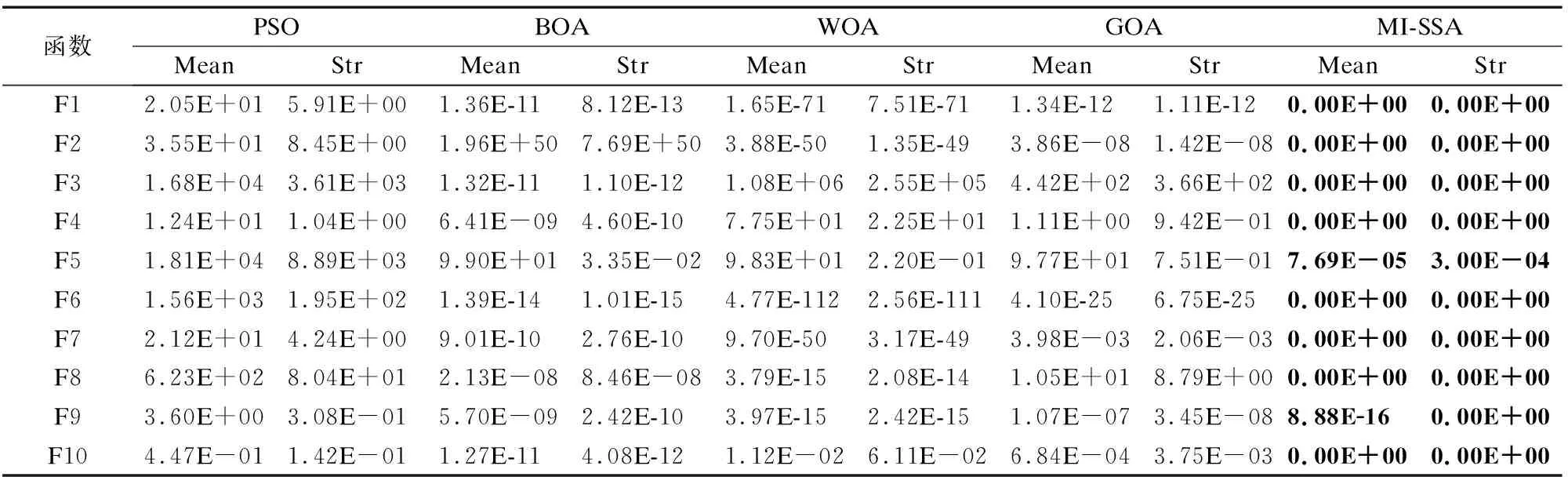
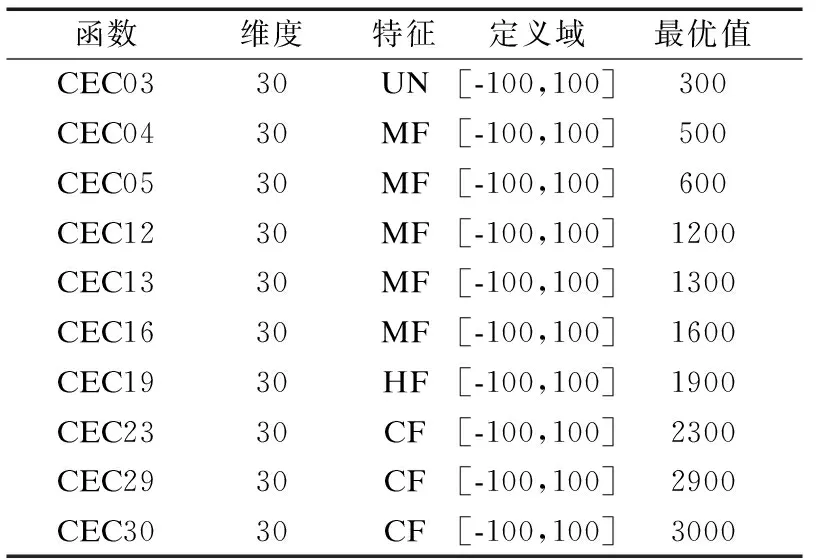
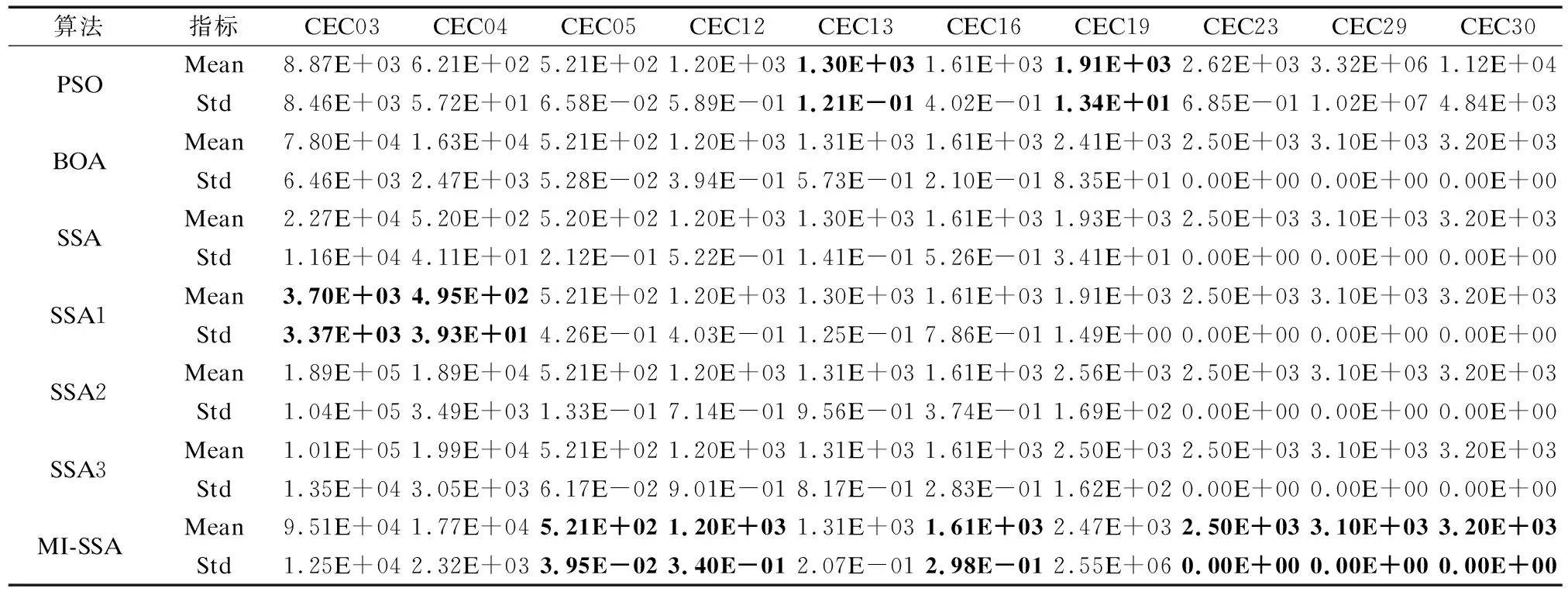
由公式(1)可以知,在R2

莱维飞行是一种步长服从莱维分布的随机游动.由于其短距离步长与偶尔较长距离步长相间的特性,莱维飞行步长能在未知范围内搜索时,能够达到更大范围,从而加强发现者的全局搜索能力,又因莱维分布用程序语言表示比较困难,通常采用Mantegna算法[23]来表示.在Mantegna算法中,其步长s的计算公式为:

(4)

(5)

其中,σν通常取1,Γ(β)是Gamma函数,根据文献[24]可知,β取值影响莱维飞行的飞行轨迹.β取值越大,越能增强算法的开发能力.

其次引入正弦函数与单位圆的关系[25],使得发现者能遍历圆上所有位置.并且通过引入黄金分割系数缩小解空间,以便获取可能好结果的搜索区域,加快算法搜索速度.综上结合莱维飞行和黄金正弦指引机制对发现者在R2

(6)

(7)

(8)

θ1=-π+2π·(1-τ)

(9)

θ2=-π+2π·τ

(10)

相较于SSA中发现者的第一段更新策略,本文提出了黄金莱维飞行策略能让发现者搜索到更大范围,如图2(b)所示.

图2 发现者搜索策略Fig.2 Search strategy of producers

3.3 t-分布扰动策略

由文献[26]可知,群智能算法引入柯西变异,能增强算法的全局探索能力;而引入高斯变异可以保证算法收敛速度.综合两者的优点,本文采用t-分布扰动策略对发现者位置进行扰动,以此来提升算法的灵活性和求解效果.

t-分布又称学生分布,含有参数自由度n,当t(n→∞)→N(0,1);当t(n=1)=C(0,1),其中N(0,1)为标准的高斯分布,C(0,1)为柯西分布.即t-分布的两个边界既是高斯分布和柯西分布[27].本文引入该特性对发现者R2>ST的更新公式进行改进,改进公式如下.

(11)

式(11)中,使用当前迭代次数t作为t分布的自由度参数.增强算法在迭代初期的全局探索能力的同时,也加强了算法在迭代后期的局部开发能力.

3.4 动态分配侦察者策略

侦察者一定程度上增强了算法的全局探索能力,并且侦察者数量占整个麻雀数量占比越高,跳出局部最优的能力越强.但是随机挑选侦查者的方式,限制了更具有活力的麻雀个体;并且麻雀优化算法中固定侦察者数量的机制,一定程度上减慢了算法运行速度.

为了挑选出更具有跳出局部极值的麻雀个体,本文采用了一种动态分配侦察者策略,一半的侦察者保持原有的随机挑选机制,另一半的侦察者引入竞争机制.侦察者执行侦察任务成功率越高,竞争能力越强.将竞争能力强的个体选入下一代的侦察者.令Ni,t表示第i个体在t代执行侦察任务的总次数,Ni,s表示第i个体在t代成功执行侦察任务的总次数,则第i个体在第t代执行侦察任务的成功率ri,t为:

(12)

式(12)中,Ni,s的大小取决于执行改进后侦察者位置更新公式(13)前后适应度的比较,即若执行侦察任务后的适应度优于执行前的适应度,则该个体执行侦察任务成功,执行侦察任务的成功总次数加一,否则保持不变.

将执行侦察任务成功率进行排序,选取成功率较高的个体(占个体总数的10%)视为更具有跳出局部最优能力的个体,并且加入下一次侦察者.

(13)

3.5 MI-SSA算法的实现步骤(图3)

图3 改进算法流程图Fig.3 Improved algorithm flow chart

3.6 MI-SSA理论时间复杂度

假设种群规模为N,最大迭代次数M,空间维度D,求解目标的适应度函数时间为f(D),由文献[20]可得,基本的SSA的时间复杂度为:O(M×N(D+f(D))),改进的MI-SSA的时间复杂度与基本的SSA相同,分析如下.

初始化阶段,假设种群初始化参数比之前多x1,且每一维度产生佳点时间为x2.则MI-SSA种群初始阶段的时间复杂度为:

O1(x1+M·N(D·x2+f(D)))=O1(M·N·(D+f(d)))

(14)

改进后的发现者位置更新阶段,假设发现者比例为ξ根据公式(6),每一维度计算levy(λ)需要的时间为x3,生成Q、α、r1、r2随机数需要的时间为x4.根据公式(11),假设生成学生分布中的随机参数,需要理论时间为x5,则MI-SSA的发现者位置更新公式的理论时间复杂度为:

O2(ξ·N·(x3+x4+x5)+M·N(D+f(D)))
=O2(M·N·(D+f(D)))

(15)

最后,动态分配侦察者策略阶段的时间复杂度与基础的SSA基本相同,该策略在理论上并没有增加算法的时间复杂度.综上所述,MI -SSA的时间复杂度为:

OSSA+O1+O2=OMI-SSA(M·N·(D+f(D)))

(16)

综上所述,本文所提MI-SSA和标准SSA的时间复杂度属于同一数量级,说明MI-SSA并没有增加算法的时间复杂度.

4 MI-SSA性能实验与分析

为了验证本文所提MI-SSA的有效性,本文仿真实验分为4个部分进行.

a)将MI-SSA与不同改进策略进行对比,验证改进策略的有效性.

b)将MI-SSA与最新的改进麻雀算法进行对比,并且引入其它改进算法进行对比实验,再次验证,MI-SSA的有效性.

c)将本文算法与其它对比算法进行Wilcoxon秩和检验,以验证不同算法之间在多个函数上的差异显著性.

d)选取部分CEC2014单峰值,多峰值,混合和复合型函数进行函数求解测试,再次验证本文算法的性能.

实验采用14个基准函数,分为3类;第1类为单峰基准测试函数,F1～F6;第2类为多峰基准测试函数,F7～F10;第3类为固定维度的多峰基准测试函数,F11～F14.

算法的基本参数:种群的规模30,最大迭代次数M=500.算法内的参数如表1所示.

表1 算法参数设置Table 1 Algorithm parameter setting

4.1 MI-SSA与不同的改进策略对比

将MI-SSA于黄金莱维策略的SSA1,t-分布扰动策略的SSA2,动态分配警戒者策略的SSA3,以及基本的SSA在空间维度分别为10/30/100/500的条件下,对14个函数进行求解.独立运行50次的数据进行统计分析,如表2、表3所示.

表2 单峰和多峰值基准测试函数测试结果Table 2 Test results of unimodal and multimodal benchmark test function

表3 固定维度多峰基准测试函数测试结果Table 3 Test results of multimodal benchmark test functions with fixed-dimension

纵向来看,MI-SSA在除去F5外的单峰值函数,在10/100/30/500维度上MI-SSA的平均值均能达到理论最优解,且标准差最小.对于函数F5,MI-SSA寻优精度和稳定性好于SSA.在多峰值函数上,随着维度的上升,标准SSA的求解精度出现下降现象,但是MI-SSA的求解精度无论是在10维度,30维度,100维度还是500维度均能取得理想的效果.

具体来说,3个改进算法对基准函数的求解上,无论平均值还是标准差上都好于SSA.说明改进策略的有效性.对于F1函数,SSA2和SSA3均能找到理论最优值,SSA1虽然没能找到理论最优值,但是相对于SSA,精确度也有近200个点的提升.对于F2函数,3个策略寻优精确度都高于SSA,其中SSA3提升最为明显,约有200多个数量级的提升.3个策略的融合的MI-SSA,能在F2函数上找到理论最优值,说明3个改进策略的互补,改进策略可靠有效.在10维度下,对于F5函数SSA的寻优精度和稳定性优于其它算法,其次是MI-SSA,但是在30/100/500维度下,MI-SSA的表现更好,其次是SSA1.这是由于随着维度的升高,搜索空间增大,求解难度加大的原因,客观说明改进后的算法在F5函数的求解上鲁棒性更好.对于F11～F14函数,MI-SSA无论是平均值还是标准差都优于SSA,提升明显.在F12求解上,结合黄金莱维飞行策略的SSA2寻优精度最高,且标准差最小,表现出较强的稳定性.

图4给出了MI-SSA、SSA、SSA1、SSA2、SSA3,以及PSO、BOA的F1～F10函数的收敛曲线图.由于部分函数收敛精度较高,本文对寻优适应度值(纵坐标)取10为底的对数,为了方便观察函数的收敛情况.由图可知,无论是单峰值函数和多峰值函数,相比SSA,MI-SSA体现了更快的寻优速度和更高的寻优精度.对于F1,F3,F6,F8,F10函数的求解,MI-SSA能在300代以内找到理论最优值,证明了算法具有很好的收敛性能.从改进的策略上来看,SSA3的寻优效果最好,其次是SSA2,SSA1次之.3个改进策略的收敛曲线大部分在SSA的收敛曲线的下方,说明3个改进策略改进的有效性.最后加入BOA,和PSO进行对比,整体来说,SSA的收敛曲线大部分都在BOA和PSO下方,说明SSA在求解F1～F10上的能力.综合MI-SSA在表3、表4和图4上的表现,充分证明3种改进策略的有效性,以及MI-SSA对于本文多种基准函数具有较强的寻优能力,特别是对于高维的函数.

图4 基准函数平均收敛曲线Fig.4 Function average convergence curve

表4 CSSA与MI-SSA算法性能比较Table 4 CSSA and MI-SSA algorithm performance comparison

4.2 与最新的群智能算法比较

目前该算法的相关文献较少,且改进麻雀算法的基本参数设置各不相同.为了进一步体现MI-SSA的有效性,本文首先引入了文献[20]中,最大迭代次数500代,种群规模为30的条件下,对其中的八个测试函数进行算法性能比较,实验结果如表2所示(“——”表示参考文献未给出相应数据).由表2可知,MI-SSA在F1,F2上的寻优精度是高于ISSA.在其他的函数上,MI-SSA寻优精度与ISSA持平.

其次将MI-SSA算法与文献[16]中的CSSA进行性能上的比较,与CSSA同一条件下独立运算50次后,对数据进行统计分析,如表5所示.由表可知,MI-SSA在其中F1～F5无论是寻优精度还是稳定性都优于CSSA算法.对于函数F8～F10,MI-SSA,CSSA优化效果相当.综上,在对于以上基本测试函数,MI-SSA均表现出较优的稳定性和寻优能力.

表5 与4种群智能算法在100维度下的结果比较Table 5 Comparison with the results of the four-species intelligent algorithm in 100 dimensions

将MI-SSA算法与PSO,BOA,WOA,GOW进行性能比较,比较结果如表5所示.对该5种算法在最大迭代次数500代,空间维度100dim,种群规模为30的条件下进行仿真实验.由表可知,MI-SSA在10个基准函数的表现,都优于其它4种算法.进一步说明改进算法的有效性.

4.3 Wilcoxon秩和检验

本文采用Wilcoxon秩和检验验证MI-SSA与其它算法的显著性差异.每次运行结果在P=5%的显著性水平下,当p值小于5%时候,拒绝H0假设,说明两种算法的差异性显著,否则就是接受H0假设,说明两种算法在整体上是相同的.由于算法不能和自身比较,所以表中的标记为“Na”表不适用,表示无法进行显著判断,“R”为显著性判断结果,“+”,“-”,“=”分别表示MSBOA算法的性能优于,劣于和相当对比算法.从表6中可以观察到大部分的p值是小于5%,“R”为“+”表示拒绝H0假设.

表6 基准Wilcoxon秩和检验P值Table 6 P-value for Wilcoxon′s rank-sum test on benchmark function

4.4 CEC2014测试函数寻优对比

为了进一步验证MI-SSA的有效性和鲁棒性,本文在CEC2014目标优化函数中选取部分单峰值(Unimodal Functions,UN)、多峰值(Multimodal Functions,MF)、混合(Hybrid Function,HF)和复合型(Composition Function,CF)的函数进行优化求解.由于CEC2014函数具有复杂的特征,大多数算法都很难找到函数最优解,所以本文选取部分函数进行测试,总结如表7所示.实验在最大迭代次数上设置为1000,算法的参数设置与前面保持一致.

表7 部分CEC2014函数介绍Table 7 Part of the CEC2014 function

将MI-SSA与SSA1,SSA2,SSA3,PSO,BOA,进行比较.部分函数独立运行30次后的结果如表8所示.在选取的10个CEC2014函数中,结合黄金莱维飞行策略的SSA1在前4个CEC测试函数上取得更优结果,MI-SSA在CEC5、CEC12、CEC16、CEC23、CEC29、CEC30上的表现优于其它5个算法.对于CEC05、CEC12、CEC13和CEC30测试函数,MS-SSA基本收敛到了理论最优值;对于复合特征CEC23、CEC29和CEC30函数,MS-SSA寻优标准差为0,说明其对于复合特征函数寻优稳定性很高.

表8 CEC2014 优化结果比较Table 8 Comparison of optimization results of CEC 2014

5 结束语

本文针对基本麻雀优化算法存在容易陷入局部最优,收敛速度慢等问题,提出了一种混合策略改进麻雀优化算法.算法初期,引入佳点集构造初始化麻雀位置来保证初始种群分布更加均匀.迭代过程中,本文提出了黄金莱维飞行策略,有效的加快收敛速度同时改善算法在迭代后期种群多样性的减少的缺陷;引入t-分布扰动策略,提升算法的灵活性和求解效果;最后提出动态分配侦察者策略,平衡侦察者全局探索与局部开采的能力.通过对14个基准测试函数和10个CEC2014基准函数仿真测试.结果表明,本文的算法在求解高维复杂函数问题上具有速度快、精度高和鲁棒性强的优势.另外通过Wilcoxon秩和检验,本文的算法表现出更优的显著性差异性.

在将来的的研究中,准备将本文提出了算法应用于实际工程优化问题.获取更好的算法性能是下一步的研究方向和重点.