混合差分进化与二次插值改进哈里斯鹰算法
2023-07-15高建瓴喻明毫
高建瓴,喻明毫
(贵州大学 大数据与信息工程学院,贵阳 550025)
1 引 言
在机器学习以及人工智能中存在许多连续的、离散的、受约束的或无约束的现实问题,同时又由于这些问题的特点,在解决这类问题存在很大的难度.因此,元启发式算法被设计来解决此类问题.元启发式算法简单易实现,其核心操作并不依赖于目标的梯度信息或其数学特征,所以在现代工程应用中广泛应用.受自然启发的元启发式算法可以分为几类:基于进化算法[1,2]、基于物理现象算法[3]以及基于群体的算法[4-7].基于群体的算法通过模拟自然界中动物的行为来进行建模从而达到优化的目的,粒子群算法PSO[4]灵感来源于鸟类群居的社会行为,其使用了很多粒子(候选解)在搜索空间中4处飞行来寻找最佳解决方案.鲸鱼优化算法WOA[5]通过模仿座头鲸捕食行为构建出搜索、包围和狩猎等的数学模型,从而达到寻优目的.薛建凯等提出的麻雀搜索算法(SSA)通过模拟麻雀寻觅食物的行为[6]构建数学模型,从而对现实问题进行优化.
哈里斯鹰优化算法(Harris Hawks Optimization,HHO)是Heidari,A.A等[7]基于哈里斯鹰捕食而构建的一种新型的群智能优化的算法.算法中包含了两个阶段:探索阶段和开发阶段,阶段之间的切换由能量因子E控制,该算法寻优效果较好.同时在工程上应用广泛,如光伏电池和模块的参数估计[8]、图像分割[9]、TDOA定位[10]等场景.
与其余元启发式算法相同,基本HHO算法同样存在对用户定义参数显示出的敏感性以及初始化种群缺失多样性、收敛速度慢、易陷入局部最优解等问题.为此汤安迪等[11]利用精英等级制度改进HHO算法,郭雨鑫等[12]利用黄金正弦优化HHO.针对基本HHO算法的几个缺点,本文在原算法的基础上进行以下几个方面的改进:1)在元启发式算法中,群体初始化分布对算法收敛性以及精度有很大影响[13].原算法对种群进行随机化初始,随机初始化种群的方式遍历性低,个体分布不均,无法全面覆盖搜索空间,使得算法性能受影响,为了提高初始种群的遍历性,提高算法寻优效率,本文使用Sobol序列初始化种群使得初始种群在搜索空间均匀分布;2)针对HHO算法探索阶段效率较低的问题,融合差分进化算法[2]加速HHO算法的寻优过程以及寻优精度,同时提高全局搜索能力;3)二次插值方式产生新个体:在HHO开发阶段一共有4个策略,在策略1、策略3中猎物都有足够能量逃跑,对开发阶段收敛速度有一定影响,为了提高开发效率,改进算法在迭代过程中选取3个个体采用二次插值方式产生下一代个体,提高哈里斯鹰包围效率.最后加入简单的精英策略选出更优的种群,增加算法的稳定性.
2 哈里斯鹰算法与差分进化算法
2.1 哈里斯鹰算法
哈里斯鹰算法灵感来自于探索哈里斯鹰的猛击猎物、突袭和不同的攻击策略.算法分为探索阶段和开发阶段,两个阶段的过度由能量因子E控制.
2.1.1 探索阶段
本阶段哈里斯鹰在栖息地通过眼睛追踪和发现猎物,哈里斯鹰随机栖息在某地,机会均等的策略发现猎物,位置更新策略如下:
(1)
(2)
其中Xrand(t)表示当前种群随机选取的个体,Xrabbit(t)表示猎物位置,Xm(t)表示当前种群的平均位置,随机参数q,ri∈random(0,1),i=1,2,3,4,[LB,UB]表示上下界,N为种群个数.
2.1.2 过度
探索到开发阶段通过能量因子E控制,公式如下:
E=2E0(1-t/T)
(3)
其中:能量因子E是猎物的逃跑能量,哈里斯鹰算法通过E判断探索和开发阶段的转换,t表示当前迭代,T表示最大迭代次数,E0表示(-1,1)之间的随机数.
2.1.3 开发阶段
在开发阶段,哈里斯鹰为了防止猎物逃跑,使用了4种策略包围猎物.用r表示猎物逃跑概率.
策略1.软包围.|E|≥0.5,r≥0.5时,猎物有充足能量逃跑.
X(t+1)=(Xrabbit(t)-X(t))-E|JXrabbit(t)-X(t)|
(4)
其中J=2(1-r5)表示猎物逃跑距离,r5是(0,1)之间的随机数.
策略2.硬包围.|E|<0.5,r≥0.5时,猎物逃跑的能量很低,哈里斯鹰会迅速突袭猎物.
X(t+1)=Xrabbit(t)-E|Xrabbit(t)-X(t)|
(5)
策略3.快速俯冲软包围.当|E|≥0.5而r<0.5时,猎物有足够能量逃跑,所以先软包围再快速俯冲攻击.在此过程加入Levy函数[14]LF模拟猎物跳跃及逃跑模型.
(6)
Y=Xrabbit(t)-E|JXrabbit(t)-X(t)|
(7)
Z=Y+S×LF(D)
(8)
其中D是所求问题维度,S是D维的随机飞行向量.
策略4.快速俯冲硬包围.当|E|<0.5而r<0.5时,猎物没有足够能量逃跑,所以先硬包围再快速俯冲攻击猎物.
(9)
Y=Xrabbit(t)-E|JXrabbit(t)-Xm(t)|
(10)
哈里斯鹰算法步骤如下:
Step1.设置种群参数(种群数量N、最大迭代次数T,迭代计数器t),随机初始化种群Xi,初始化Xrabbit位置.
Step2.计算每个个体适应度,更新Xrabbit位置.进入循环.
Step3.计算能量因子E、猎物逃跑距离J、逃跑概率r.如果|E|≥1|,则使用公式(1)更新个体位置,如果|E|<1,根据2.1.3节中的不同策略包围猎物,更新个体位置.
Step4.判断是否达到终止条件,如果没有则返回Step 2,否则终止迭代输出最优位置以及对应的适应度值.
2.2 差分进化算法
差分进化DE算法是一种直接搜索算法,与遗传算法相似,进化过程包含了变异、交叉、选择3个部分,DE算法通过个体之间的差分量实现个体变异以及种群进化,本文主要结合差分进化算法种群变异以提高HHO算法探索性能,差分进化种对每个个体向量Xi(t),i=1,2…,NP,差分进化算法基本变异策略如下:
Xi(t+1)=Xr1(t)+F·[Xr2(t)-Xr3(t)]
(11)
其中r1,r2,r3为(1,NP)之间互不相等的整数且不等于i,F∈[0,2]是一个常数因子.
3 改进的哈里斯鹰算法
3.1 Sobol序列初始化种群
元启发式算法性能在一定程度上受初始种群的影响,在搜索空间中分布均匀的种群能保证较高的遍历性、多样性,提高算法效率[14].为了提高算法全局搜索能力,国内外学者使用混沌映射初始化种群,卓然等利用混沌Tent映射[15]初始化种群,倪龙雨等使用Logistic混沌映射扰动最优解[16]来优化算法.Arora等[17]采用 Circle 混沌方法初始化种群.Gehad等[18]使用多种混沌映射嵌入搜索代理中以提高搜索效率.
这些混沌算法虽然具备一定的跳出局部最优解的能力,但还存在随机性强和相邻点紧密相关的性质的缺点,比如Tent映射最小周期点(0.2,0.4,0.6,0.8)和不稳定点(0,0.25,0.5,0.75)[19].为此本文采用Sobol序列初始化种群,Sobol属于低差异序列,相比伪随机序列,低差异序列在给定空间分布更均匀,其任意长度子序列都能均匀填充函数空间[20].Sobol序列周期短,采样速度快,在处理高维问题上效率更高[21].于是根据Sobol序列初始化的种群如下:
xn=xmin+Kn·(xmax-xmin)
(12)
其中Kn∈[0,1]是Sobol序列产生的随机数.[xmin,xmax]是最优解取值范围.图1所示为在[0,1]之间产生维度为9、种群数量为200的初始随机序列与在[xmin,xmax]范围内产生的Sobol序列对比,可以看出Sobol序列分布更均匀.

图1 两种方式随机产生(0,1)之间的随机数Fig.1 Random numbers between randomly generated (0,1)
3.2 融合DE算法
HHO的主要缺点之一是其不擅长于探索解空间,它依赖于能量因子控制算法探索和开发.为了解决这一局限性,提高HHO探索能力,解决HHO过早收敛的问题,本文将HHO和具有良好探索能力的DE算法进行杂交,以改进HHO探索能力弱的缺点.结合DE算法之后,为了更好平衡探索阶段和开发阶段,引入了一个新的控制参数λ,当rand≤λ时,算法进入探索阶段,否则为开发阶段.λ通过如下公式调整:
λ=1-(t/T)
(13)
其中T是最大迭代次数,t是当前种群迭代次.本文使用λ来控制算法的探索和开发能力,λ的值根据公式(14)调整,随着时间的推移从1降到0.
3.3 二次插值法
优化算法在进入开发阶段后对局部搜索能力要求更高,局部搜索能力差会导致算法陷入局部最优解,原HHO算法的开发阶段分为了4个策略,其中策略1、策略3依赖于猎物逃跑距离J从而陷入被动局面,为了能够主动预测探索猎物下一步位置,本文使用二次插值方式在目标位置进行探索,从而主动出击,以便跳出局部最优解.二次插值法基本思想是在搜索区间中不断使用二次多项式去近似目标函数,并且逐步用插值多项式的极小值点去逼近搜索问题的极小值点.
首先在目前种群中选取最优解A(a1,a2,…,aD),A具有最优适应度值(也就是Xrabbit),然后再随机选取两个个体B(b1,b2,…,bD)、C(c1,c2…,cD).其中D是要求解问题的维度.则X′(t+1)(x1,x2,…,xD)为这3个个体产生的下一代个体,公式如下:
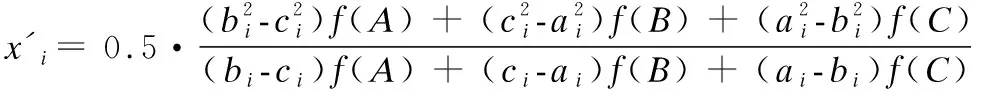
(14)
其中f(A)、f(B)、f(C)分别表示A、B、C的适应度值.新产生的个体X′(t+1)(x1,x2,…,xD)必然是二次曲线的极小值点.策略1、策略3在改进时也有不同,策略1中哈里斯鹰位置更新公式直接使用式(14),策略3哈里斯鹰需要俯冲攻击猎物,更优的位置有利于捕食,所以本文通过比较公式(6)和式(14)产生的下一代,从中选取最优的个体.公式如下:
X(t+1)=min(f(X(t+1)),f(X′(t+1)))
(15)
在min()函数中X(t+1)由公式(6)得来,X′(t+1)由公式(14)计算得到.同时,改进算法中包含了简单的精英模式:每次循环得到的个体是父代和子代之间更优的个体.
3.4 改进哈里斯鹰算法流程
结合3.1-3.3节,本文改进的哈里斯鹰算法(IHHO)流程如下:
Step1.设置种群参数(种群数量N、最大迭代次数T,迭代计数器t),使用公式(12)初始化种群Xi,随机初始化Xrabbit位置(最优位置).计算初始种群个体适应度f.
Step2.根据适应度更新Xrabbit位置.
Step3.计算能量因子E、猎物逃跑距离J、逃跑概率r、控制参数λ,产生随机数rand.
Step4.判断;如果rand≤λ,算法进入探索模式,根据公式(11)更新个体位置.如果rand>λ,进入开发模式.再根据能量因子E和逃跑概率r判断包围策略,其中策略1使用公式(14)更新位置,策略3使用公式(15)更新.策略2、策略4分别使用公式(5)、公式(9)更新位置.
Step5.计算子代适应度f′,如果f′ Step6.判断是否达到终止条件,如果没有则返回Step 2,否则终止迭代输出最优位置以及对应的适应度值. 为了验证IHHO的性能,本文使用了12个基准函数进行测试,这12个测试函数中分为3类:单峰函数(f1(x)~f5(x)):常用来检测算法寻优能力和收敛速度;常用来检测算法寻优能力和收敛速度;多峰函数(f6(x)~f9(x)):测试算法 全局搜索能力和避免算法陷入局部最优解的能力;固定维度函数(f10(x)~f12(x)):测试算法探索和开发之间的平衡能力,如表1所示. 表1 测试函数集Table 1 Test function set 对比算法的参数设置:粒子群算法PSO、飞蛾扑火算法MFO[22]、灰狼优化算法GWO[23]、哈里斯鹰算法HHO参数设置分别与相应参考文献相同;麻雀搜索算法SSA:发现者比例PD=0.2、侦察者比例SD=0.1、警戒阈值R2=0.8;差分进化算法DE变异策略为:DE/rand/1,变异概率为0.9;鲸鱼优化算法WOA常数b设置为1. 本文选取平均值和标准差作为算法性能的度量标准.评价标准中:平均值用于衡量算法的求解精度,标准差用于衡量算法鲁棒性.实验环境:操作系统为Windows10、CUP:Intel Core i5-7500,编译器Pycharm,各算法程序使用Python编写. 本文首先用每个算法每个测试函数测试,其中多维度测试函数(f1(x)~f9(x))维度为30维,每个算法独立运行30次,以验证算法的稳定性及收敛性,结果如表2所示. 表2 函数测试结果Table 2 Function test results 分析表2对12个测试函数的测试结果可知,IHHO在寻优结果均值更接近于函数理论全局最优值,同时多个测试函数重复独立实验得到的标准差更小,说明算法鲁棒性强,寻优精度相较于PSO、GWO、MFO、DE、SSA、WOA以及HHO好.在求解单峰函数时,只有函数f2效果略低于WOA.其余单峰测试函数效果均优于其他算法.同时改进算法在单峰测试函数与固定维度测试函数中的寻优表现优于HHO算法,多维测试函数寻优结果中f9表现好于HHO算法,其余多峰测试函数寻优结果相差不大.函数f5的全局最小值处于抛物型凹陷曲面,曲面最速下降方向与到达全局最优值的方向近似垂直,PSO、GWO、SSA、DE等算法都很难近似全局最优解,IHHO在此函数上求解能力最强.对于所有测试函数,IHHO在f1、f3~f5、f9、f11~f12上效果最好,在f6~f8上寻优效果与HHO算法相似.表2 中同样对8个算法的寻优能力进行排序,整体上看IHHO算法性能更佳. 除精度之外,本文还比较了不同算法的寻优时间,用于评价算法时间效率,表3中给出了每个函数30次独立实验寻优时间.可以看出IHHO算法中总耗时略高于DE算法与HHO算法,比其他算法耗时低. 表3 优化过程耗时Table 3 Optimization process time consuming 图2中给出的收敛曲线进一步比较了IHHO算法和7个对比算法的性能,图中所示IHHO算法在500次迭代中均能收敛最优解,同时除了f11、f12之外IHHO算法收敛速度均快于其他对比算法,在函数f11的收敛曲线中IHHO比GWO、HHO算法略慢,且所有算法在早期均能收敛于最优解并趋于稳定.由测试函数f12的结果可以看出,虽然IHHO算法前期收敛速度不及GWO、WOA、DE、MFO、PSO等算法,但是在迭代后期,IHHO算法能更接近全局最优解.整体来看IHHO算法在f3、f5、f9、f12这几个函数的收敛速度上相比于HHO算法提升较为明显,其余函数上略有提升,但IHHO算法精度高于HHO算法. 图2 IHHO与其余算法收敛曲线对比Fig.2 IHHO convergence curves are compared with the other algorithms 仅通过比较算法在不同函数上30次独立实验的平均值与标准差并不能精确比较算法每次运行结果,因为运行结果具有一定偶然性,因此为了估计算法之间统计学上的显著性差异,使用Wilcoxon非参数检检验,该检验不限定两独立样本必须满足正态性,而是基于样本的秩次排列.为此在显著性水平为0.05条件下对比IHHO算法和其他算法的显著性差异,当检验p值小于0.05说明对比算法存在显著性差异,否则的话说明对比算法寻优结果整体相同.由表4中可以看出,IHHO与PSO、MFO、GWO、DE、SSA、WOA在11个测试函数上有显著性差异.与HHO对比在8个测试函数上有显著性差异.由以上分析结果可知,IHHO算法在测试函数上的寻优效果好于其余7个对比算法. 表4 IHHO对比其余算法Wilcoxon 统计检验结果Table 4 IHHO compared the results of the Wilcoxon statistical test for the remaining algorithms 为了探讨本文不同改进策略对算法的影响,于是使用了3个改进策略IHHO1、IHHO2以及IHHO3和HHO、IHHO进行比较,取8个测试函数,实验独立运行30次,实验结果如表5所示.分析表5中结果,使用Sobol序列初始化种群(IHHO1)与结合DE算法改进策略(IHHO2)对于固定维度函数的寻优效果改善明显,二次插值法(IHHO3)对多维度测试函数寻优效果改善较为明显.使用这3种策略混合提出的IHHO效果明显好于HHO. 表5 不同策略结果对比 Table 5 Results results of different strategies 文献[11]利用混沌精英等级制度提出改进HHO算法CEHHO,文献[12]利用黄金正弦优化HHO提出了EGHHO,本次实验使用12个基准函数与这两种改进算法进行对比,重复独立实验30次并比较结果,实验结果如表6,本文改进算法在多峰测试函数上表现优于另外两种改进算法,在单峰测试函数中与其余两种改进算法相差不大.总体来看IHHO有7个测试函数的寻优效果好于EGHHO与CEHHO,图3所示给出了6个函数的收敛曲线,从曲线看出IHHO在函数f10上收敛速度明显快于EGHHO与CEHHO,其余函数则相差不大. 表6 与不同改进算法对比Table 6 Contrison with different improved algorithms 图3 不同改进算法收敛曲线Fig.3 Convergent curves of different improved algorithms 以上实验结果分析验证了IHHO在低维搜索空间的有效性,展现出了较强的寻优能力,但一般算法在高维搜索空间性能会急剧下降,为了验证IHHO在高维搜索空间的稳定性,本文选取6个测试函数(f1~f3,f6~f8)分别设置3个维度为100维、500维以及1000维,算法独立运行30次验证算法在高维搜索空间有效性,实验结果如表7所示. 表7 高维空间优化测试结果Table 7 High-dimensional spatial optimization of the test results FunSSA100D500D1000DWOA100D500D1000DHHO100D500D1000DIHHO100D500D1000Df1Mean2.13E+045.78E+041.53E+051.08E-681.32E-704.70E-693.33E-072.49E-063.56E-068.32E-824.14E-833.70E-77Std.ev2.77E+033.46E+035.90E+035.82E-686.48E-702.30E-686.32E-077.41E-065.72E-064.47E-812.21E-821.99E-76f2Mean1.12E+024.26E+029.64E+028.32E-499.53E-481.33E-482.43E-041.18E-031.70E-033.64E-411.20E-421.23E-42Std.ev7.63E+001.48E+011.66E+014.21E-484.36E-475.86E-484.44E-042.12E-032.56E-031.88E-403.00E-423.96E-42f3Mean1.97E+058.04E+053.17E+061.15E+063.05E+071.22E+081.91E+001.45E+021.14E+031.02E-512.76E-071.95E-06Std.ev8.53E+043.32E+051.29E+063.66E+051.49E+074.12E+073.89E+003.78E+022.36E+033.75E-511.48E-061.00E-05f6Mean8.64E+022.77E+037.02E+037.58E-150.00E+000.00E+005.68E-074.01E-062.54E-060.00E+000.00E+000.00E+00Std.ev3.97E+018.93E+011.74E+024.08E-140.00E+000.00E+001.30E-061.03E-055.20E-060.00E+000.00E+000.00E+00f7Mean1.36E+011.26E+011.30E+013.64E-153.05E-154.23E-155.54E-054.52E-056.15E-054.44E-164.44E-164.44E-16Std.ev4.48E-012.88E-011.58E-012.65E-152.04E-151.82E-155.54E-056.61E-056.90E-054.44E-164.93E-321.48E-31f8Mean1.73E+025.30E+021.36E+037.40E-180.00E+000.00E+003.12E-071.11E-068.53E-070.00E+000.00E+000.00E+00Std.ev2.04E+013.36E+017.19E+012.77E-170.00E+000.00E+003.12E-072.65E-062.99E-060.00E+000.00E+000.00E+00 通过表7结果可知,PSO、GWO与SSA虽然稳定,但其在高维搜索空间中的寻优效果较差,在1000维搜索空间中,MFO与DE算法在函数f2上出现无法优化的现象,WOA在测试函数f2上出现了性能下降的现象,其余测试函数则保持了一定的稳定性.HHO算法在高维搜索空间中寻优效果也有所下降,整体来看,只有IHHO在高维空间中仍然能够保持较好的优化效果,体现了IHHO算法的稳定性. 哈里斯鹰优化算法近年来提出的一种新颖的优化算法,本文针基本HHO算法存在收敛速度慢,寻优精度低等问题提出了混合差分进化以及二次插值法改进的哈里斯鹰算法IHHO,改进算法在初始化阶段使用Sobol序列初始化种群分布,提高算法初始种群在搜索空间中的遍历性,为提高全局搜索能力奠定基础;HHO算法探索阶段全局搜索能力低,于是本文融合了DE算法的变异策略,以提高算法全局搜索能力;最后在开发阶段,针对哈里斯鹰包围不主动的缺点,使用二次插值方式产生下一代,增加主动性,提高算法在局部搜索时的能力,同时加入简单的精英策略以保证算法稳定性.将IHHO与其余6中算法以及HHO算法进行实验对比,结果表明IHHO在单峰测试函数、多峰测试函数、固定维度测试函数上均有较好的表现,在收敛速度以及收敛精度上优于对比算法,在寻优耗时上,IHHO耗时同样低于大部分对比算法.4 实验结果分析
4.1 算法参数与测试函数集
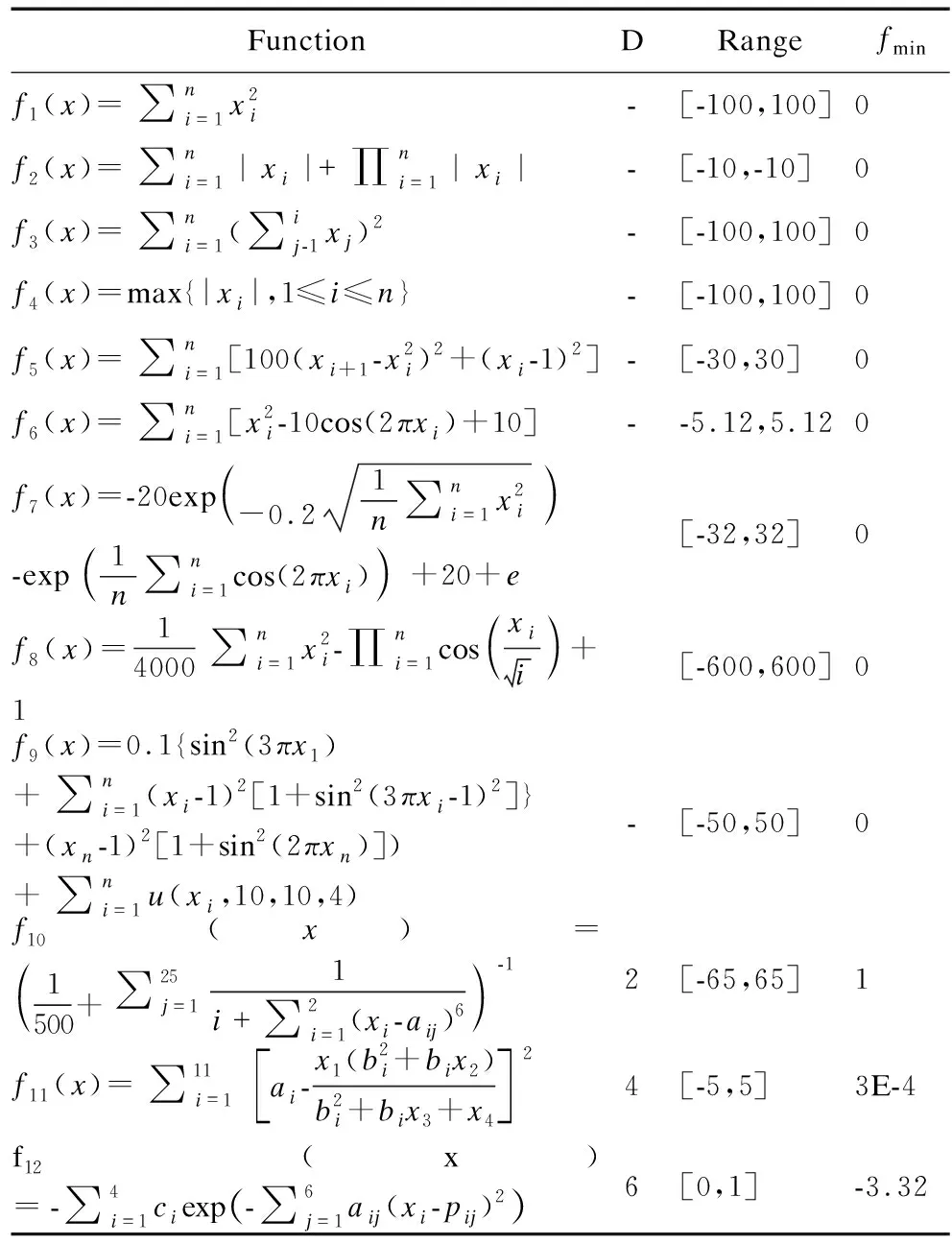
4.2 30次独立实验结果分析


4.3 收敛曲线分析
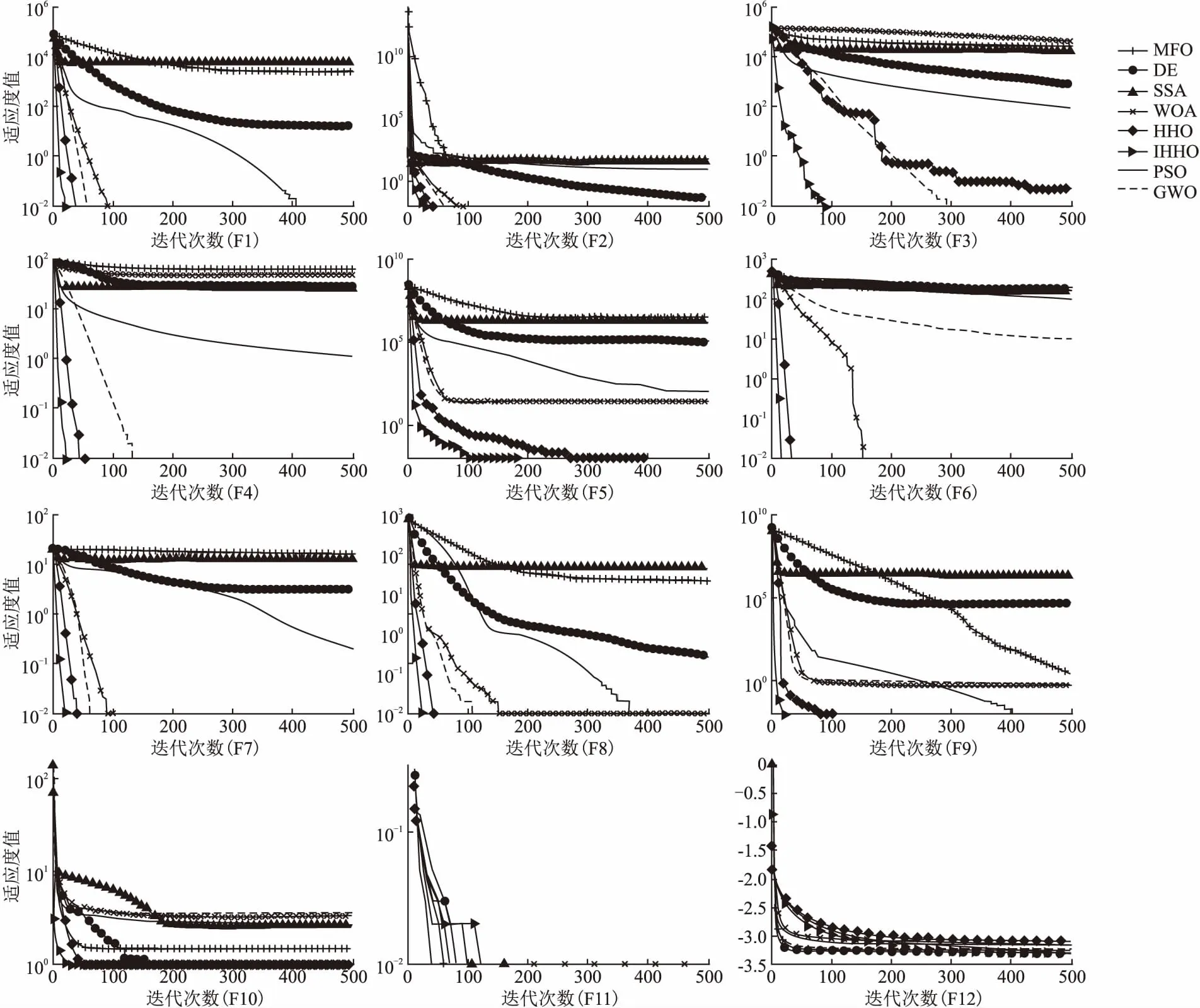

4.4 不同改进策略分析
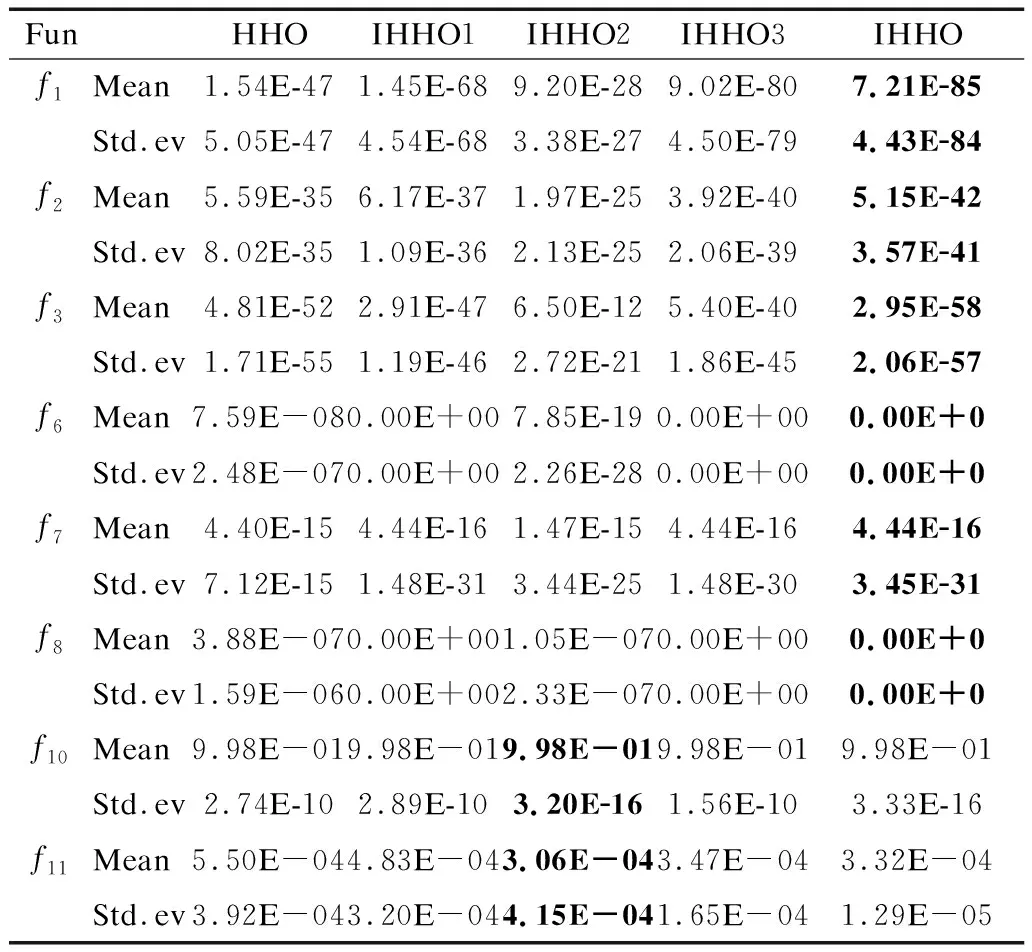
4.5 与其他改进对比


4.6 高维优化实验分析


5 结 语
