一种基于优先级的云工作流动态调度方法
2023-07-15范贵生陈兴鹏虞慧群
范贵生,陈兴鹏,虞慧群
1(华东理工大学 信息科学与工程系,上海 200237) 2(上海市计算机软件测评重点实验室,上海 201112)
1 引 言
随着云计算和云基础设施的快速发展,越来越多的工作流应用正在从传统的分布式平台向云端过渡.工作流调度是一个众所周知的NP难题[1],其旨在为工作流中的每个任务分配计算资源以满足如时间、能耗和成本等性能指标.一个工作流可以通过一个有向无环图来表示,其中节点代表工作流的每个任务,边代表任务之间的依赖关系.用户对应用的请求被描述为一个工作流,应用服务器将工作流中的每个任务分发到相应的云服务进行执行,以优化任务执行周期[2].
当现有服务实例不能满足工作流的性能要求时,通过创建新的服务实例以实现执行成本和系统性能之间的折衷[3].云提供商提供具有不同处理能力和租赁成本的服务资源,用户根据需求选择不同的服务类型和服务数量,以满足应用工作流的时间约束和执行成本.当用户面临服务选择时,一般的方法是在满足工作流的最后期限的同时,最小化工作流的执行成本,有两大类方法可以解决这个问题:局部启发式和元启发式.目前,无论启发式算法还是元启发式算法,主要关注的是调度方案是否能够满足工作流的一个整体时间约束,而不是具体到是否满足工作流的每个任务的子截止时间.而且,在任务调度过程中基本上是基于工作流任务优先级的静态调度,并没有根据云中服务资源的可变性,动态调整工作流任务调度优先级.
基于以上问题,本文提出了一种基于优先级的动态调度算法(Priority-based and Dynamic Scheduling,Pbads)来解决满足时间约束的工作流任务调度问题.主要工作如下:
1)根据工作流任务之间的依赖性,将相关联的多任务合并为单任务,以降低在调度过程中不同服务之间的数据传输成本.其次,根据用户工作流的时间约束,为每个任务分配其子截止期限,并基于任务的子截止期限和计算任务的紧急程度,也即调度优先级.根据任务的优先级对工作流中的任务进行排序,生成调度队列.
2)在任务调度过程中,Pbads基于时间约束动态调整任务调度优先级和子父任务调度决策,为每个任务分配一个成本增量最小的服务.对于每一个服务,每当分配一个新的任务时,Pbads会遍历该服务的执行队列的每个可插入位置,可以是队列的头部、队列的尾部以及每个任务的前后位置,判断当前执行位置是否为可以满足任务子期限和依赖约束,并在可行位置中选择一个任务执行成本最小的位置.
3)在实验中,本文将Pbads方法与现有方法(ProLiS[4]、L-ACO[4]、COHA[5]、CPDE[6]和IC-PCP[7])使用4种数据集进行实验比较.结果表明,Pbads算法在执行成本和满足工作流时间约束方面具有更好的表现.
本文的其余部分安排如下:第2节介绍了工作流调度的相关工作.第3节是工作流调度的成本优化问题模型.第4节提出了云中工作流动态调度方法.最终的实验结果在第5部分.第6节是对当前工作的总结和未来工作的展望.
2 相关工作
传统的分布式系统中,工作流调度工作关注如何最小化工作流的执行时间,而云环境中工作流的执行成本也是一个不可忽视的因素,因此如何权衡工作流的执行时间和执行成本尤为重要.
为了解决基于截止期限的工作流调度问题,文献[4]提出了一种启发式算法ProLiS和一种元启发式算法L-ACO.ProLiS算法为每个工作流任务分配子截止期限,根据任务的紧急程度建立了一个有序的任务列表,并将每个任务分配给满足其子截止期限且成本增量最少的服务.L-ACO算法是基于蚁群算法来解决时间约束的成本优化问题:蚂蚁通过更新信息素轨迹,查找全局最优解.然后每只蚂蚁都为问题建立一个解决方案,存储局部最优的解决方案,然后更新信息素轨迹,整个过程不断重复,直到返回全局最优解.文献[5]设计了一种任务拆分算法COHA,该算法将无法满足子截止期限的工作流任务拆分为两个子任务,为其分配子截止期限,并添加到任务队列中进行重新调度,以此来确保所有的任务都能按时完成.文献[6]基于关键路径提出了一种的成本预测算法CPDE,该算法通过使用现存虚拟机和创建新虚拟机两种方式来满足工作流截止期限约束,并通过预测每个任务调度成本以此来确定工作流整体调度成本最低的方案.文献[7]基于工作流部分关键路径提出一种的启发式算法IC-PCP,该算法通过递归的方式,从已分配的任务出发构造局部关键路径,每个关键路径上的任务被安排到成本最低且满足子截止期限约束的虚拟机上.文献[8]提出了一种主动响应式工作流调度算法,当新工作流到达时,该算法仅将当前所有工作流的就绪任务进行混合调度,在满足截止期限的约束下选择执行成本最小的虚拟机.文献[9]提出了一种时间预算双重约束的调度算法BDAS,该算法对工作流结构进行分层,将工作流任务划分为若干无关联性的包任务,以增大调度过程中的并行程度.文献[10]考虑到私有云有限的资源以及隐私暴露的风险,提出了一种在混合云环境下,成本与隐私感知的调度算法CPHC,该算法在满足工作流截止期限和隐私保护需求的前提下,尽可能多的将工作流任务调度到私有云环境,以此来最小化工作流执行成本.文献[11]改进了基于遗传算法的批处理工作流任务的调度算法BIGA,基于独立任务和非独立任务两种任务类型,进行调度成本优化.文献[12]基于已知的HEFT算法,提出了一种预算和期限约束算法BDSD,该算法基于工作流任务的子截止期限定义任务的调度优先级,并考虑预算和期限双重约束下的调度成功率.文献[13]提出了一种多约束的工作流调度算法,该算法基于最慢执行效率的虚拟机计算工作流可用预算,以此来构建可用虚拟机集合,并定义了一个平衡因子,针对每个工作流任务开发了一种资源选择方法,以满足工作流任务的时间约束的前提下最小化其执行成本.文献[14]提出了EIPR算法,该算法利用预分配资源的空闲时间和预算盈余来复制任务,随着可用于复制的预算增加,同时也增加了满足工作流最后期限的可能性,减少了应用程序的总执行时间.文献[15]提出了一种截止期限感知的启发式算法DCEDA,该算法通过工作流最短执行时间来确定其截止期限,通过实时监控资源池,动态为工作流任务分配执行成本最低的虚拟机.文献[16]提出了一种分而治之的调度算法DQWS,该算法首先为工作流关键路径上的任务选择满足截止期限并且执行成本最低的资源,然后将关键路径上的任务从工作流中移除,工作流分为若干子工作流,针对每个子工作流重复上述过程直到全部任务分配完成.
为了解决基于预算约束的大规模多任务工作流调度问题,文献[17]提出了一种预算敏感的调度算法ScaleStar,该算法将当前需要分配的任务分配给更好的计算资源执行,有效平衡了工作流的执行时间和成本.文献[18]提出了一种公平预算约束的调度算法FBCWA,该算法通过对工作流任务进行分类,通过调整成本时间因素,为每个工作流任务提供一种公平的预算约束调度算法.文献[19]提出了一种异构预算约束调度算法HBCS,旨在在用户定义的执行成本下最小化工作流任务的执行时间,其主要贡献在于该算法实现了更低的时间复杂度.文献[20]提出了一种基于任务复制的调度算法TDSA,该算法回收已分配工作流任务未使用的预算资源并进行重新分配,利用资源上的空闲时间槽选择性地复制任务的前驱任务,从而在保证工作流任务的子预算约束的同时减少任务的完成时间.文献[21]基于云的计算资源构建工作流的性能分析模型,并提出了一种临界贪婪算法,以在云预算约束下实现科学工作流的最小端到端延迟.文献[22]根据工作流任务优先级为其分配预算约束,并且优先保证工作流关键路径任务分配至最佳虚拟机,其他任务按照更新的预算成本选择合适的虚拟机.文献[23]等扩展了经典的异构最早完成时间算法并提出了BHEFT,它决定是否使用用户设置的特定约束,并在截止日期和预算约束的前提下工作.文献[24]提出了一种资源分配机制和工作流调度算法GRP-HEFT,旨在现代IaaS云小时成本模型中最小化给定工作流的完成时间,提出了一种贪心算法,通过服务实例的效率列出实例类型,并在预算约束下选择效率最高的实例.
总之,无论是基于成本约束还是时间约束的工作流调度,都在优化性能方面做了很多努力.但是很多工作是基于整个工作流维度的,而不是特定于工作流中的每个任务.而且在调度过程中,没有考虑到云中资源的可变性,任务的调度顺序是静态的,不会随着调度过程而变化.因此,本文试图从工作流任务维度入手,考虑到云服务的异构性和任务之间的依赖性,动态调整任务的优先级以及调度策略.
3 工作流调度模型
3.1 系统模型
当用户向应用程序发出请求时,应用程序会将请求以工作流的形式在云端执行.工作流可以用一个有向无环图表示,WF=(Nodes,Edges),其中Nodes表示工作流任务的集合{t1,t2,…,tn},任务之间相互独立,并且具有不同工作负载twi;Edges则是不同任务之间的依赖关系的集合,edgei=(ti,tj)表示任务ti和tj之间的依赖关系或优先级,只有当ti完成后,tj才能开始执行.datai,j表示ti到tj之间的数据传输量,因此只有当ti执行完成并且数据传输完成后,tj才能开始执行.为了形象地描述一个工作流,方便后续工作的开展,为每个工作流添加两个工作负载为零的任务tentry和texit,将这两个任务作为工作流的入口任务和出口任务.具体工作流示例如图1所示.
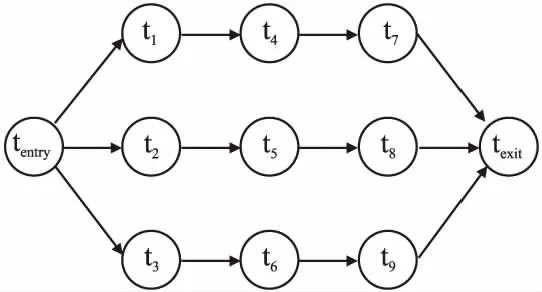
图1 工作流结构图Fig.1 Workflow structure diagram
云中存在一组具有不同处理能力和不同租赁成本的服务集合Service={sl},工作流的执行成本按照在工作流执行期间租用云中服务的租金来表示.本文根据按需定价模型计算工作流的执行成本,工作流执行成本根据工作流使用云中服务的时间间隔数进行计算,例如小于一个时间间隔会按照一个时间间隔计算.使用TI表示一个时间间隔,对于服务sl,使用Calc(sl)表示服务的处理能力,使用Cost(sl)表示服务在一个时间段内的租用成本.
当任务ti分配给服务sl进行执行时,ti的工作负载为twi,sl的处理能力为Calc(sl),因此ti的执行时间可以计算为:
ET(i,l)=twi/Calc(sl)
(1)
假设云中所有的服务资源都在同一个区域内,因此不同服务之间的带宽bw大致相等,同一服务中的传输延迟为零.因此,不同任务之间的数据传输时间取决于任务所分配的服务以及任务之间的数据传输量.ts(ti)表示任务ti所分配到的服务,数据传输时间TT(i,j)可以通过以下方式计算:
(2)
如果将任务ti分配给服务sl进行执行,RT(i,l)表示服务sl可以执行ti的最早开始时间.那么任务ti的开始执行时间ST(i,l)和完成时间FT(i,l)可以计算为:
(3)
FT(i,l)=ST(i,l)+ET(i,l)
(4)
服务的总租赁时间可以通过服务租赁开始时间RSTl和租赁结束时间RETl来计算,并将服务总租赁时间转换为时间间隔数来计算服务的使用成本MSC(sl).那么MSC(sl)可以通过以下方式计算:
MSC(sl)=「(RETl-RSTl)/TI⎤×Cost(sl)
(5)
此外,云中服务sl的租用时间从部署在sl上的第一个任务ti接收其父任务数据开始,到部署在sl上的最后一个任务tj执行完成且数据传输完成时结束:
(6)
(7)
3.2 问题描述
工作流旨在将每个任务分配给相应的服务进行执行以满足用户的需求.因此任务调度可以用
(8)
工作流执行总成本WFC(R,M)可以通过以下方式获得:
(9)
使用D表示用户指定的工作流的截止期限.因此满足时间约束的云工作流成本优化问题定义为:
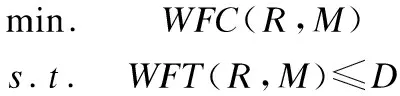
(10)
4 基于优先级的动态调度算法
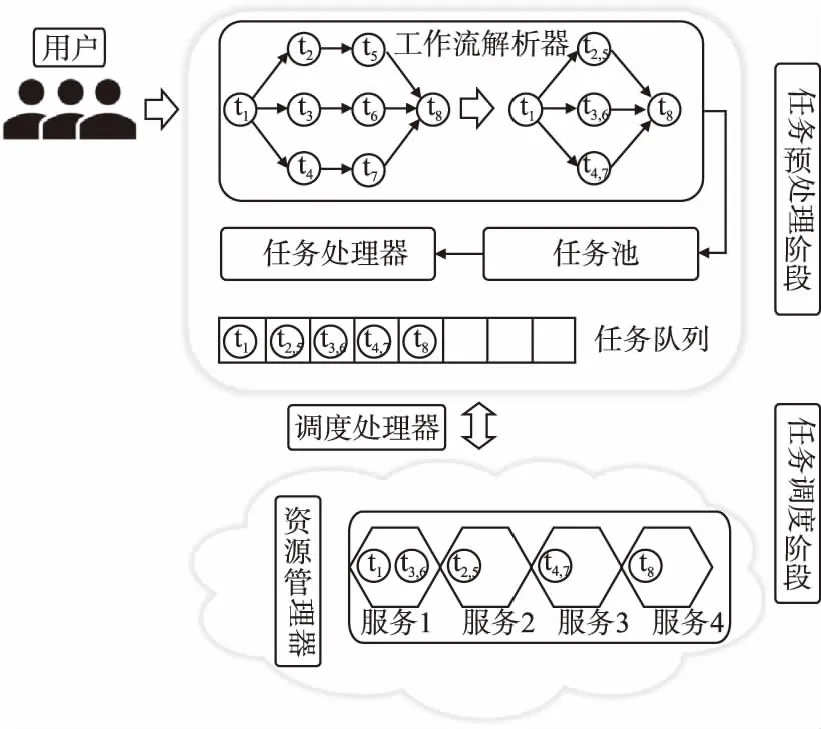
图2 工作流调度模型Fig.2 Workflow scheduling model
4.1 任务预处理阶段
1)任务合并.为了减少工作流调度过程中的不同服务之间的数据传输开销,将多个相关联的工作流任务被合并为单个任务(图3).这不仅降低了多个任务之间的数据传输成本,而且还减少了循环监控调度信息时产生的时间开销.工作流任务合并条件如下:任务ti是任务tj的父任务,当ti有唯一的子任务tj,且tj有唯一的父任务ti时,ti和tj合并为ti+j.当ti和tj被分配到不同的服务上执行,就会产生任务之间的数据传输成本,而任务合并就会避免成本的产生.算法1规定了任务合并的具体步骤.注意:ti为除出口任务texit以外的所有工作流任务,其中任务下标索引i的变化范围为[0,n-1),n为当前工作流任务总数.
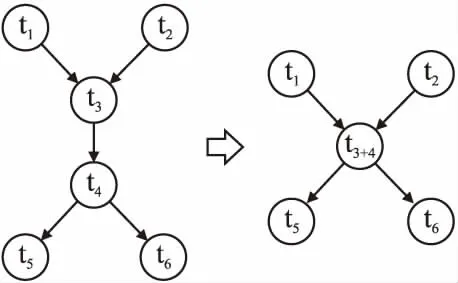
图3 任务合并示例图Fig.3 Task merge example diagram
2)任务截止期限分配.在本文中,依据文献[4]中的所提出的方法为工作流中的每个任务分配子截止期限.任务ti的子截止期限tdli由其任务等级tri决定的.任务等级的含义类似于工作流的关键路径,即从任务ti到出口任务texit的预期执行时间的长度.任务等级是通过从出口任务texit向前遍历来计算得到的,并为每个任务选择最快的服务s*计算任务执行时间,其原因是考虑到调度问题的第一个目标是满足截止期限约束.因此任务等级tri可以通过以下方式获得:
(11)
dj表示是否考虑任务的数据传输延迟[4].ccrj是任务tj的执行时间与任务通信的比率,即(twj/Calc(ms*))/(datai,j/bw),rand()是一个随机函数,用于返回[0,1]中的随机数,o是一个大于1的参数:
(12)
通过入口任务到当前任务的最长路径,按比例的为工作流中的每一个任务设置一个子截止期限tdli.
(13)
3)任务排序.为每个工作流添加两个执行时间为零、传输时间为零的任务tentry和texit,并将这两个任务作为工作流的入口和出口.此外,根据任务紧迫性对工作流任务进行排序,任务紧迫性ui可以通过以下方式获得.
(14)
其中tdli表示任务的子截止期限,ni表示从任务ti到任务texit的关键路径上的任务数量.因此,当任务的子截止期限越小,到任务texit的关键路径上的任务越多,即u值越小,任务的紧急度越高.
依托在中国、亚洲、澳洲、欧洲、美洲成立的五大研发中心,聚力斐雪派克、GE Appliances、海尔、卡萨帝、统帅五大顶级厨电品牌,相信未来海尔会推出更多行业领先的厨电产品,满足不同用户的个性化、多样化需求,创造出更加舒适、更加健康的厨房环境。
算法1.任务合并算法
输入:由n个任务组成的工作流WF=(Nodes,Edges)
输出:任务合并完成后的工作流WF=(Nodes,Edges)
1.通过入口任务tentry生成任务队列Queue;
2.foreach 任务tiinQueuedo
3.ifti有唯一子任务tjthen
4.iftj有唯一父任务tithen
5. 更新任务tj的工作负载twj=twi+twj;
6. 更新任务tj的父任务集合;
7. 更新任务ti的父任务的子任务集合;
8.end
9.end
10.将ti从任务队列Queue移除;
11.end
4.2 任务调度阶段
工作流任务调度的主要过程如算法2所示.首先,根据任务之间的依赖关系将多个任务合并为单任务,并为每个合并后的任务分配子截止期限.然后,根据每个任务的子截止期限和该任务到出口任务关键路径的任务数计算该任务的调度优先级.最后,根据任务调度优先级对工作流任务进行排序生成任务队列,并根据任务队列依次对任务进行调度分配.
算法2.任务调度算法
输入:R←ø,M←ø
输出:任务资源映射结果
1.调用任务合并算法进行工作流任务合并;
2.Queue=基于任务优先级初始化任务调度队列;
3.foreach 任务tiinQueuedo
4.listp=任务ti及其已调度的直接父任务集合;
5.collectionc=listc的调度序列的集合;
6.listmin=collectionc中满足任务时间约束和依赖关系,且执行成本最低的序列;
7. for each 任务tpinlistmindo
8. 调用服务选择算法选择执行成本最小的服务sp;
9.if服务sp属于已分配的服务资源Rthen
10. 将服务sp添加到R中;
11.end
12. 计算任务tp在服务sp上执行的开始时间ST(tp,sp)和完成时间FT(tp,sp);
13. 更新M←
14.listt=分配给服务sp的任务队列;
15.foreach 可插入位置piinlisttdo
16. 将任务tp插入到pi位置进行队列重排序;
17.if重排序后的队列调度顺序满足每个任务的子截止期限和依赖关系then
18.计算该队列调度的执行成本;
19.end
20. 将tp插入到一个执行成本最低的位置;
21.end
22.end
23.listc=任务ti的未调度的直接子任务集合;
24.collectionc=listc的调度序列的集合;
25.foreach 序列qiincollectioncdo
26. if 序列qi满足任务的子截止期限和依赖关系then
27. 计算当前调度序列qi的执行成本;
28.end
29. 选择执行成本最低的调度序列更新Queue
30.end
31.end
32.返回
考虑到父任务与子任务在不用服务之间的所产生的数据传输成本,因此当一个新的任务被调度时,会获取当前任务且已经调度完成的父任务集合,并与当前任务形成一个局部调度队列,动态调整任务的调度策略以实现当前调度成本增量最小化.具体过程如下:首先遍历局部调度队列,为每个任务选择一个全局成本增量最小的服务(第6行),具体过程见算法3.然后更新任务的开始执行时间和完成时间,并得到任务ti所分配的服务sl的当前任务队列.遍历服务任务队列的所有可插入位置,如任务队列的第一个位置,任务队列中每个任务后面的位置,以及任务队列的末端.判断将当前任务ti插入到该位置后,服务任务队列是否满足任务之间的依赖关系以及任务的子截止期限约束,并计算所有可行的服务任务队列的执行成本.通过比较执行成本,选择一个成本最低的插入位置(第13~20行).
每当一个任务调度完成后,获取该任务的未调度的子任务集合,根据当前的调度信息动态调整子任务集合中每个任务的的调度优先级,生成一个执行成本增量最小的局部调度序列,并以此修改任务队列的整体调度顺序,从而达到动态调整任务优先级的目的(第21~31行).
算法3主要目的是为任务选择一个执行成本增量最小的服务,具体过程如下:首先,从已分配服务资源池中选择一个满足任务子截止期限约束且执行成本增量最小的的服.注意,该处的成本增量的计算方法是添加任务ti后服务sl的执行成本减去添加ti前的服务执行成本.如果服务资源池中不存在既满足任务子截止期限,且服务执行成本增量最少的的服务,那么则从服务资源池中选择任务执行时间最短的服务.此外,若所选择的服务不是处理效率最快的服务类型,那么将其更新为最快的服务类型.服务候选者包括解决方案(即M)中已经使用的所有服务,以及那些尚未使用但可以随时添加到M中的服务.
算法3.服务选择算法
输入:任务ti
输出:服务sl
1.TTmax=任务ti与其子任务之间最大的数据传输时延;
2.Pool=正在执行任务的的服务资源池;
3.foreach 服务slinPooldo
4. 计算任务ti在服务sl上执行的开始时间ST(ti,sj)和完成时间FT(ti,sl);
5.ifFT(ti,sl) 6. 计算任务ti在服务sl上执行的成本; 7.end 8. 选择一个满足任务子截止期限且执行成本最低的服务sl; 9.end 10.ifPool不存在满足上述条件约束的服务then 11.sl=服务资源池中执行任务ti时间最少的服务; 12. 计算任务ti在服务sl上执行的开始时间ST(ti,sl)和完成时间FT(ti,sl); 13.ifFT(ti,sl)>tdli且服务sl不是处理速度最快的服务then 14. 将sl更新为处理速度最快的服务; 15.end 16.end 17.返回服务sl 基于由n个任务组成的工作流进行算法时间复杂度分析.Pbads算法,工作流任务的最大依赖为n(n-1)/2,故截止期限分配阶段的时间复杂度为O(n2),基于优先级进行任务排序的时间复杂度为O(nlogn),任务调度阶段,服务候选者数量的上限是n+s,其中s是服务类型的集合,在任务循环调度过程中,遍历候选服务的时间复杂度为O(n(n+s)).考虑当前任务的父任务调度决策和子任务优先级动态调整,并且当新任务到达服务时进行插入重排,分配给每个服务的最大任务数为n,因此任务调度阶段的时间复杂度为O(n2(n+s));因此Pbads算法时间的复杂度为O(n2(n+s)). ProLiS算法,为每个工作流任务分配子截止期限的时间复杂度为O(n2);候选服务数量上限为n+s,因此ProLiS算法的时间复杂度为O(n(n+s)).L-ACO算法,大小为colSize的蚁群迭代maxNo次,共构建colSize×maxNo个解,基于ProLiS算法的工作流任务调度过程,L-ACO算法的时间复杂度为O(colSize×maxNo×n(n+s)).COHA算法,将n个任务组成的工作流拆分后最大任务数为2n;候选服务数量上限为2n+s,因此COHA算法的时间复杂度为O(2n(2n+s)).CPDE算法,有s种虚拟机类型,候选虚拟机数量上限为n+s,因此CPDE算法任务调度过程的时间复杂度为O(n(n+s)).IC-PCP算法,对n个任务组成的工作流构造局部关键路径,最大可用资源数为n+s,因此IC-PCP算法的时间复杂度为O(n(n+s)). 在任务数量为n,可用资源数量为n+s的情况下,ProLiS算法、CPDE算法、IC-PCP算法和COHA算法每调度一个任务需要遍历一遍可用资源,而COHA算法任务拆分后任务数量最大为2n,可用资源数量为2n+s,因此COHA算法复杂度大于其余3种算法.而Pbads算法在调度完任务后需要遍历可用资源上已分配任务,因此Pbads算法复杂度大于上述4种算法.L-ACO算法需构建colSize×maxNo个解,每个求解过程复杂度为O(n(n+s)).综上所述,本文提到的6种算法的复杂度对比如下:L-ACO算法>Pbads算法>COHA算法>ProLiS算法、CPDE算法、IC-PCP算法. 本节详细阐述了实验设置和实验指标,进行了模拟实验,并将实验结果与现有方法进行比较. 基于模拟实验,使用4种不同科学工作流(CyberShake,LIGO,Montage和SIPHT)来评估所提出的Pbads方法.这4种工作流应用在结构、依赖关系和通信数据等方面各不相同,图4描述了每种应用的一个简单工作流结构. 图4 4种科学工作流结构示例Fig.4 Example of four realistic scientific workflows 图4(a)CyberShake工作流应用于地震科学,通过生成地震分布图来描述一个地区的地震严重程度,它可以被归类为数据密集型的工作流,对服务内存和CPU有很大的要求;图4(b)LIGO工作流应用在引力物理学中,检测宇宙中各种事物产生的引力波,这个工作流任务是CPU密集型任务,需要消耗大量内存;图4(c)Montage是一个天文学应用,用于生成天空的自定义马赛克,其大部分任务是I/O密集型,不需要太多的CPU性能;图4(d)SIPHT用于自动搜索NCBI数据库中细菌复制子的非翻译RNA.关于以上4种工作流的详细信息,可以参考文献[25]进行了解和学习.从每个工作流选择4种规模,分别是50、100、200和300个任务,此外对于每种规模都使用了20个服务实例. 实验中,假设云服务提供商提供5种不同类型的服务,每种服务都有不同的处理能力和执行成本,具体信息如表1所示.每一种服务的配置及其处理能力是基于EC2云服务的性能分析[26].服务的定价是基于亚马逊EC2的现行定价方案.参考文献[27]中的设置,将不同服务之间的平均带宽设置为20MBps,这是亚马逊网络服务中提供的近似平均带宽,并计费间隔TI设置为一小时. 表1 不同服务类型的处理速度和成本表Table 1 Processing speed and cost table for different service types 此外,引入松弛系数λ来表示截止期限的宽松程度,MF和MC表示工作流分别在效率最快的服务和成本最低的服务上执行的成本,工作流的截止期限可以通过以下方式确定. D=MF+(MC-MF)×λ (15) 对于任务等级定义中的参数o,参考文献[4]中的方法,分别使用1、1.5、2、4、8、10这6个值测试了Pbads在4种不同工作流程中的表现,λ取值从0到0.2,步长为0.02.结果表明,Pbads在o取值为1.5时表现最好,因此在下面的实验中,o设置为1.5. 将本文方法Pbads与ProLiS、L-ACO、COHA、CPDE、和IC-PCP 进行比较,对于每个工作流,使用上述6种算法来计算其执行成本.但是每一种算法,都会存在不满足最后期限约束的解决方案,因此只比较每种算法解决方案的执行成本是不全面的.针对上述问题,引入算法成功率的概念,即每种算法成功调度的工作流数量与总调度的数量的比率.通过比较算法成功率和其解决方案的执行成本来综合评估算法的有效性. 在实验过程中,按照步长为0.005,将松弛系数λ从0.005递增到0.05,以此评估上述6种算法方法在满足任务截止期限约束的前提下执行工作流的有效性(成功率)和执行效率(执行成本).图5描述了6种算法基于松弛系数由小到大的过程中,平均成功率的变化折线图.由图5可以发现,λ值越大,即工作流截止期限越靠后,算法的总体成功率越高.本文提出的Pbads算法在CyberShake数据集中略逊于L-ACO算法,在其余3种数据集中成功率表现最优. 图5 λ在0.005至0.05变化情况下,每种算法的成功率Fig.5 Success percentage of each approach with λ varying from 0.005 to 0.05 图6描述了在不同的松散系数λ下,6种算法的标准化成本.由图6可以发现,随着松散系数值越大,工作流的执行成本越低.对比其余4种算法,在LIGO、Montage和SIPHT这3种工作流数据集中,无论截止期限因子λ变化如何,Pbads算法整体的执行成本都小于其他5种算法. 图6 λ在0.005至0.05变化情况下,每种算法的执行成本Fig.6 Normalized cost of each approach with λ varying from 0.005 to 0.05 图7描述了6种算法在不同任务数下工作流调度的时间开销情况.可以看出,随着任务数的增加,工作流调度所消耗的时间随着增加.ProLis、COHA、CPDE和ICPCP算法所花费的调度时间开销较低,随着任务数的增加,时间开销变化并不明显.本文提出的Pbads算法和L-ACO算法时间复杂度较高,因此随着任务数的增加,所需要的时间开销明显上升,这也是后续工作需要改进的地方. 图7 5种算法的工作流任务调度时间Fig.7 Workflow task scheduling time of five algorithms 本文提出了一种基于优先级的云工作流动态调度算法Pbads,该算法在满足任务期限的前提下,最大程度地降低执行成本.在截止期限的松弛系数从小到大变化的情况下,Pbads在执行成本和满足工作流截止期限约束方面都具有更好的表现.在未来的工作中,将研究在满足任务期限的前提下,如何实现从任务到服务、服务到虚拟机的多层映射,以降低工作流任务的执行成本以及工作流调度的时间开销.4.3 算法复杂度分析
5 实验与分析
5.1 实验设置
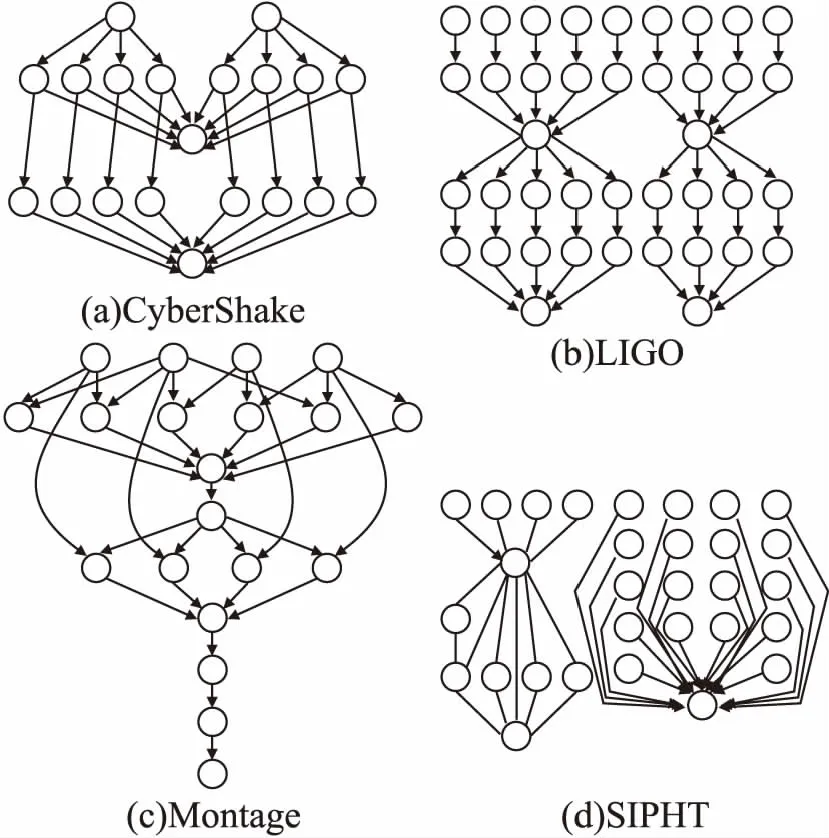
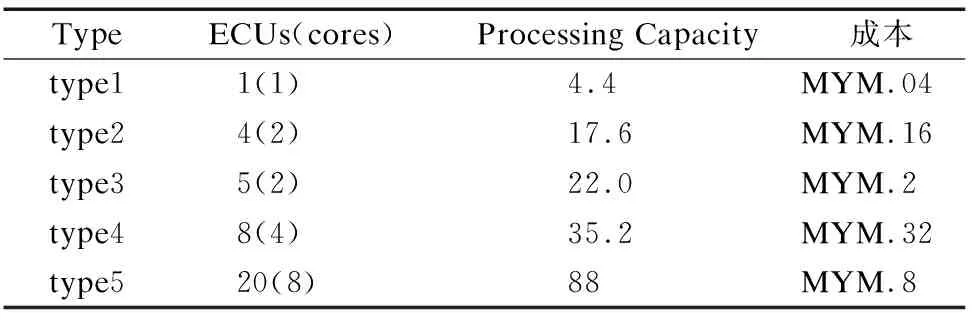
5.2 度量指标
5.3 结果分析
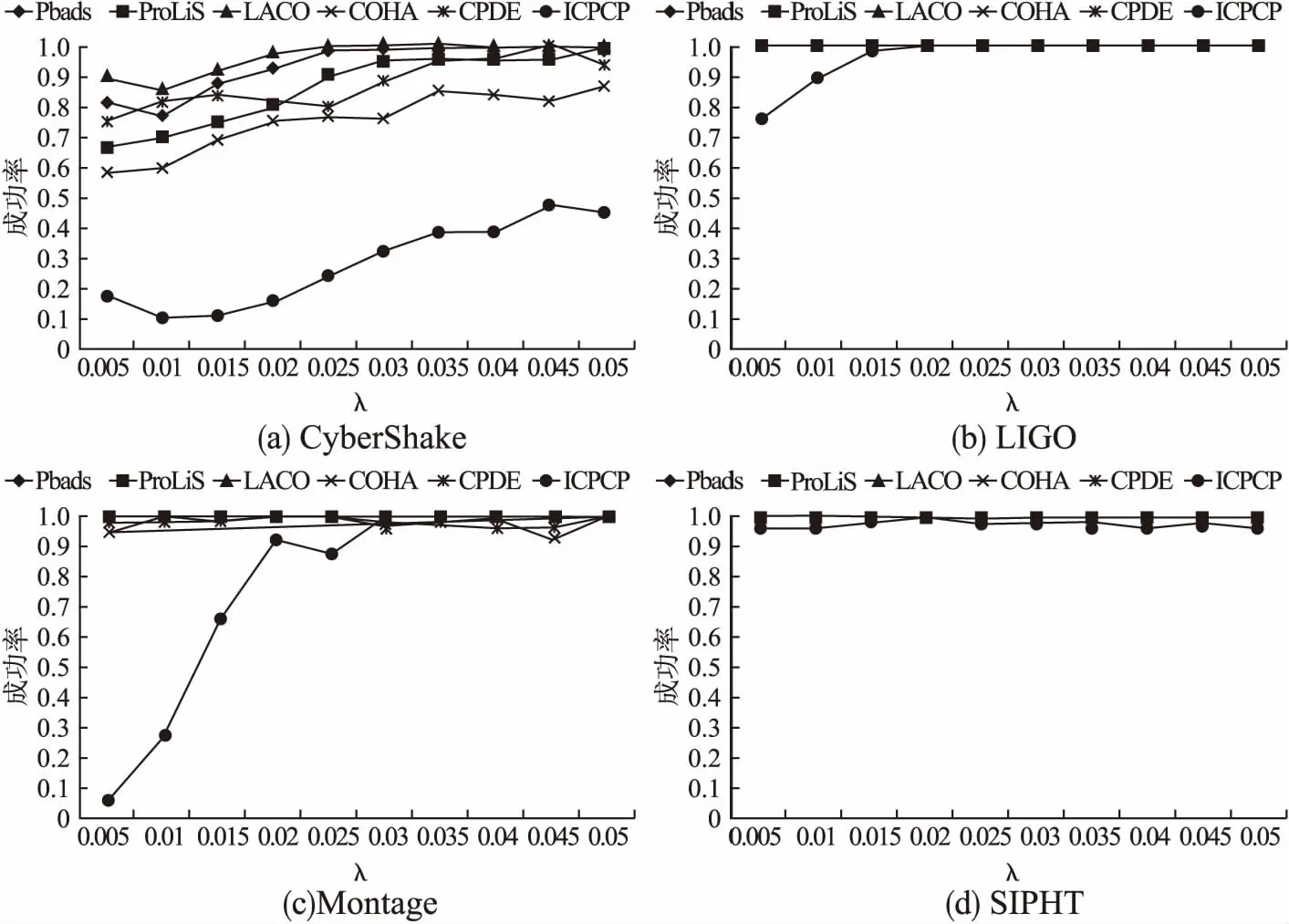

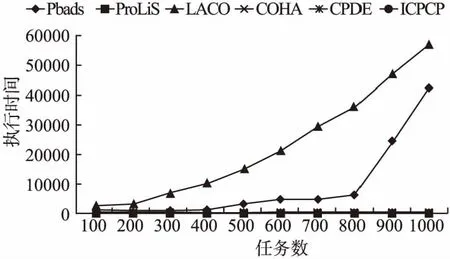
6 结 论
