基于非负矩阵分解的次声信号分类方法∗

孟子轩 程 巍 张天予 吕 君 滕鹏晓

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院噪声与振动重点实验室 北京 100190)

(3 中国科学院大学 北京 100049)

0 引言

次声是指频率低于20 Hz 的声信号。自然环境与人类社会中广泛存在着次声信号，许多物理现象在发生和发展过程中都会伴随低频次声信号的产生，例如自然活动中的地震、台风、闪电、火山喷发和海啸以及人类活动中的核和化学爆炸、火箭发射、飞机起飞等事件[1]。从灾害预防的角度看，对次声信号的识别分类能够起到预警的作用；在军事对抗领域，通过次声信号来识别敌对方的军事活动对国防安全具有十分重要的意义。

自1996 年全面禁止核试验条约组织(Comprehensive nuclear-test-ban treaty organization,CTBTO)成立以来，次声成为国际监测系统(International monitoring system,IMS)所使用的4种主要监测核爆的手段之一，利用机器学习方法对次声信号进行识别分类的研究也由此展开[2]。对于次声信号的识别分类任务而言，由于样本数量较少，因此研究的关键问题在于信号的特征提取[3−4]。吴涢晖[5]采用了8 种不同的特征提取方式对化学爆炸、闪电和台风3 类事件进行处理，对比了支持向量机(Support vector machines,SVM)、BP神经网络、长短时神经网络和卷积神经网络(Convolutional neural network,CNN) 4 种分类器的分类性能，结果表明SVM的识别性能最好。同时指出，其构建的分类流程对人工设计的特征有较高的要求，需要研究人员对各种信号的特征进行深入的研究和挑选，以找出区分度较大的特征。

谭笑枫等[6]以数据驱动为出发点，采用CNN进行特征提取、模型训练和识别分类，以简化特征设计过程，其提出的方法在CTBTO 提供的化爆与地震两类次声数据集上达到了82.72%的准确率，但该方法对数据量的要求较高，难以应用于小样本数据集的情况。本文从矩阵分解的角度，考虑采用浅层的模型对次声信号进行特征提取，以适用于小样本场景下的次声信号分类任务。

戴翊靖等[7]考虑到次声信号特性与样本量小的特点，采用非负矩阵分解(Non-negative matrix factorization,NMF)进行次声降噪。该方法的研究对象为一段混合的次声信号，将预训练的平稳噪声作为监督项，通过NMF 方法将信号中的目标部分与噪声部分分离，然后恢复目标信号。其目的在于获得较高信噪比的目标信号，以便于后续的次声监测任务。本文聚焦于分类的具体应用，对于大气次声波的产生和传播机理研究以及次声事件的影响和防治策略都有重要意义。特别是本研究使用的NMF 方法处理结果是在可靠的先验信息标注的多条数据库上获得的，其目的在于提取目标信号的基本组成部分，分别作为不同类信号的特征。特征提取后使用SVM 等分类器完成识别分类任务，是次声监测的重要环节，也是大气次声学的一项基础性研究。

1 特征提取算法及分类模型

1.1 NMF理论

NMF 是一种广泛应用于图像识别、语声增强以及声事件识别等领域的算法[8−10]，其基本框架由Lee 等[11]提出。定义非负矩阵V ∈Rf×t，此处非负的含义是指V中的任一元素Vij≥0。NMF 的目的是希望得到两个非负矩阵W与H，同时保证二者乘积与一个V尽可能接近：

在本文中，V为原信号经短时傅里叶变换(Short-time Fourier transform,STFT)后得到的时频图，而W ∈Rf×d与H ∈Rd×t则表示经训练后从数据中学习到的特征，其具体含义往往与实际问题相关。W可以认为是V中的基本组成部分，被称为字典矩阵，其列向量被称为字典原子；而H被称为激活矩阵，表示在V中这些部分在相应时间点上的线性组合计权，其行向量被称为字典原子的激活系数；参数d则表示字典矩阵中字典原子的个数[12−13]，此时有

式(2)中，wi与hi分别为字典原子与相应的激活系数。由于通常设定d ≪min(f,t)，即只用很少的字典原子来描述原信号，因此只有在W包含了原信号中最主要的组成时，才会使得式(1)成立[12]，本文将这些表示原信号基本部分的字典原子作为特征输入，采用SVM等分类器进行识别分类任务。

W和H可通过最小化V与WH之间的距离度量函数得到，即求解如下的优化问题[11]：

式(3)中，D表示V与WH之间的距离度量函数，其定义为

式(5)中，i=1,2,···,f；j=1,2,···,t。应用梯度下降法对式(5)进行迭代求解，J(W,H)分别对Wil与Hlj的偏导数为

其中，l=1,2,···,d，T表示矩阵转置。则基于梯度下降法的迭代规则，由式(6)和式(7)可得

其中，λil和µlj是迭代步长。乘性更新法则对步长进行限制，规定其取值为

将式(10)与式(11)分别带入式(8)与式(9)中，得到欧几里得距离度量下的乘性更新法则：

式(12)与式(13)的非增性在文献[15]中得到了证明。可以看出，采用式(12)与式(13)迭代求解式(3)时只进行乘法和加法运算，从而保证了迭代过程及结果的非负性。

对于不同的距离度量函数而言，其乘性更新法则可采用统一的形式给出[13]：

式(14)中，β的不同取值代表采用不同的距离度量函数，◦表示对矩阵元素的乘法，同时指数运算和除法运算均表示对元素的运算。

1.2 分类模型

一个完整的识别分类系统如图1 所示。分类模型的选择主要包括传统机器学习算法与深度神经网络两类。SVM 是一种广泛应用于次声信号识别分类领域的机器学习模型，由于其分类面完全由支持向量确定，因此在小样本场景下有较好的表现性能[16]。

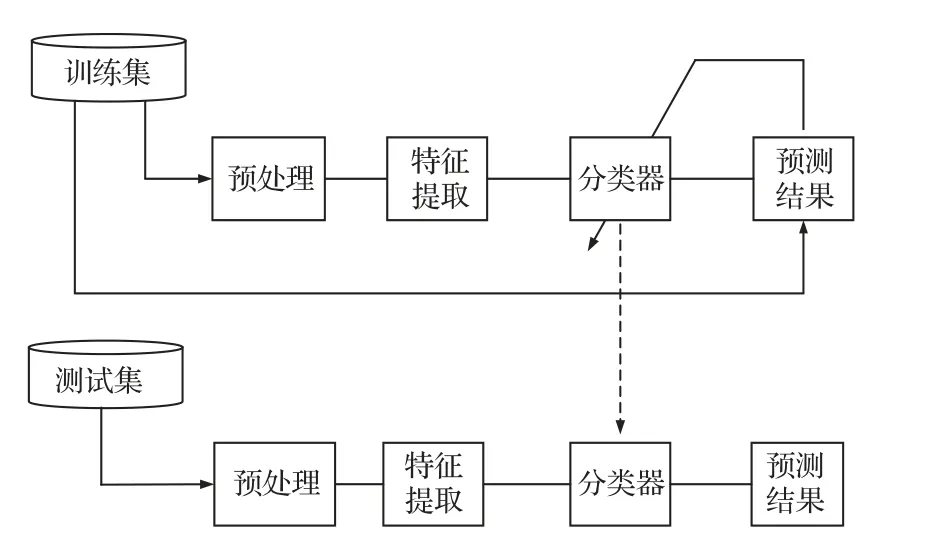
图1 识别分类系统框图Fig.1 Block diagram of the classification system

SVM 的基本模型是定义在特征空间上的间隔最大的二分类线性分类器[14]，即求解如下的优化问题：

式(15)中，w为分类超平面的法向量，xi为第i个输入，yi为输入对应的标签，b则表示超平面的偏置量。式(15)是在数据集线性可分的情况下得到的，又被称为线性可分SVM。对于一般的线性不可分数据集，通常是对式(15)添加惩罚项，允许部分样本不满足约束，则式(15)可改写为

式(16)中，ℓ(·)表示损失函数。若采用合页损失函数，同时引入松弛变量ξi≥0，可以得到线性SVM模型，如下：

采用拉格朗日乘子法，可以得到式(17)的对偶问题，如下：

式(18)中，αi表示拉格朗日乘子。式(15)与式(18)到的SVM 分类面均为线性分类面，通过采用核技巧，可以得到更为一般的SVM形式，如下：

式(19)中，κ(·)表示核函数。若选用线性核函数，则式(19)退化为式(18)。几种常用的核函数包括线性核、高斯核、多项式核等，需在实际使用时进行选择。以上提出的SVM 均为二分类模型，对于K种类别的多分类问题，目前最常用的方法是分别构建K个独立的SVM[17]：当训练第k个模型时，使用当前类别yk作为正样本数据，而将其余的K−1 个类别作为负样本。

由于所提特征是一种二维数据，因此同时使用CNN 进行分类。LeNet-5 是一种经典的CNN 结构[18−19]，其网络结构如图2所示。

图2 CNN 结构图Fig.2 CNN structure diagram

LeNet-5 是一种较为浅层的CNN，其输入经过两层卷积层、两层池化层后与全连接神经网络相连，最后输出其类别概率。为保证泛化能力，每层网络均添加正则化项，并采用Dropout进行随机失活。

2 分类设计与实验结果分析

2.1 数据来源及预处理

中国科学院声学研究所计划在全国范围内建设广域多台阵次声监测网络，现已在新疆、辽宁、云南等地建设了固定式次声台阵，并通过机动式次声探测站对酒泉、文昌等发射基地的次声信号进行收集。通过逐步多通道相关方法等阵列处理算法得到每个信号的相速度、入射角和声源位置等声学参数，并结合声源信息的验证，对于信号的类别可以进行准确的标注，经过准确标注的实测数据集为本研究奠定了重要的基础，有利于推动我国次声监测技术的发展，对于自然灾害预警以及国防建设等领域具有重大意义。

本文使用的数据为通过实地布阵自行采集的次声时域信号，数据集大小为105 条，包括4 种类型的信号，其中爆炸信号17 条，地震信号22 条，闪电信号41条，再入信号25条。本文采用原信号进行过STFT 后的时频图作为输入。4 类信号经STFT 后的时频图如图3所示。

图3 4 类信号时频图Fig.3 The spectrograms of four kinds of signals

图3 所有标注出的红色方框区域均为信号部分。就信号的频率维特征而言，爆炸事件与地震事件的主要频率分布在5 Hz 以下，其中地震事件在该频带中的分布比较均匀，而爆炸事件则分布在2∼4 Hz，相对集中；闪电事件的频带较宽，在20 Hz以上仍有部分信号，主要部分明显地集中在5 Hz 和15 Hz 左右，分成了两个部分；再入事件的频率则分布在15 Hz 以下，主要部分在5 Hz 以下，持续时间较短。从时频图上可以看出各信号之间存在明显差异。由于各个信号均为实际采集信号，则不可避免地混有了噪声成分，这干扰了识别分类任务。为了找出目标信号的主要部分，同时对原始数据进行降维，需要进行特征提取工作。图3中呈现的4类次声波频谱随时间的变化，和持续时间的长短都有显著的差异，其形成机制复杂，本研究尚未涉及，暂时搁置，留待进一步的研究。

本文采用NMF 对图3 所示的4 类信号时频图进行特征提取。在NMF 中，字典原子个数d是需要预先设置的参数，可采用经验的参考取值[20]，但在实际应用时仍需进行调整。首先对图3 所示的4 类信号进行NMF 分解，采用欧几里得距离作为代价函数，迭代次数设置为200 次，在d=8 时得到的爆炸信号收敛曲线如图4所示。

图4 爆炸信号收敛曲线Fig.4 The convergence curves of four kinds of explosion signals

图4 中黑实线表示全部事件的度量函数值平均值，上下两条虚线则分别表示全部事件度量函数值的上下限。为了保证特征能够充分反映原始信号，要求选取的迭代次数使得信号的距离度量函数充分收敛。从图4 中可以看出，经过50 次迭代后度量函数已趋于收敛，同时经实验验证，继续增大迭代次数对于分类准确率的影响不大，综合计算效率与分类准确率，本文选取迭代次数为200。4 类信号经NMF分解得到的W矩阵与H矩阵如图5所示。

图5 4 类事件NMF 分解结果Fig.5 NMF decomposition results of four kinds of events

图5 中左侧为信号的字典矩阵，右侧为激活矩阵。结合图3 与图5，可以看出字典矩阵是对信号时频谱的一种降维表示，不同类之间的字典矩阵有明显差异，因此本文选取W作为信号的特征向量进行分类实验。

2.2 实验环境

本文使用的数据集中训练集与测试集的比例为7 : 3，由于数据量有限，因此不再设计验证集，而是在训练时采用四折交叉验证的方式进行模型选择。识别分类实验包括两部分，分别是基于经验模态分解(Empirical mode decomposition,EMD)和NMF 的识别分类实验。分类实验在AMD®4600H平台上进行，操作系统为Windows10，所用软件为Python3.6.8，CNN 的开发框架为Tensorflow2.4.0，SVM模型由Sklearn模块提供。

2.3 实验结果与分析

2.3.1 基于EMD的分类过程

基于EMD 的特征提取主要是对分解得到的各阶本征模态函数(Intrinsic mode function,IMF)分量进行处理[3,5]，可选择的处理方式包括计算分量各阶矩、能量、信息熵、波形特征、分量比等，经处理后的各分量仍可继续提取其能量、信息熵或波形特征等特征。本文采用时域能量、时域熵、EMD能量、EMD 熵、EMD 奇异值以及希尔伯特边际谱(Hilbert marginal spectrum,HMS)[21]4 种特征作为对比。以HMS 为例，对识别分类过程进行说明。提取HMS 时首先对时域信号进行EMD，将得到的IMF进行希尔伯特变换，构造出原信号的解析信号，从而得到原信号的希尔伯特谱，HMS 即为希尔伯特谱的时间维积分结果，反映了瞬时频率的时域幅值累加。对得到的HMS进行主成分分析(Principal component analysis,PCA)，取前30维作为SVM输入进行分类。本文采取随机优化的方式对SVM 进行参数选择，以相同条件进行100次分类实验，在测试集上的分类结果如图6所示。

图6 HMS-SVM 测试集分类结果Fig.6 Test set classification results of HMS-SVM

图6中横坐标为HMS-SVM在测试集上的分类准确率，纵坐标则表示在100 次实验中不同准确率出现的次数，蓝色柱状图为实验数据记录，红色曲线为使用正态分布拟合的结果。从图6 中可以看出，HMS-SVM 在测试集上的分类准确率最大值为87.5%，平均值为69.76%，方差为7.65%，多数分类结果集中在60%∼80%之间。本文还提取了时域能量、时域熵、EMD能量、EMD熵等4 种特征，在上述实验条件下进行分类实验，分别使用SVM 与一维CNN作为分类器，其结果见表1。

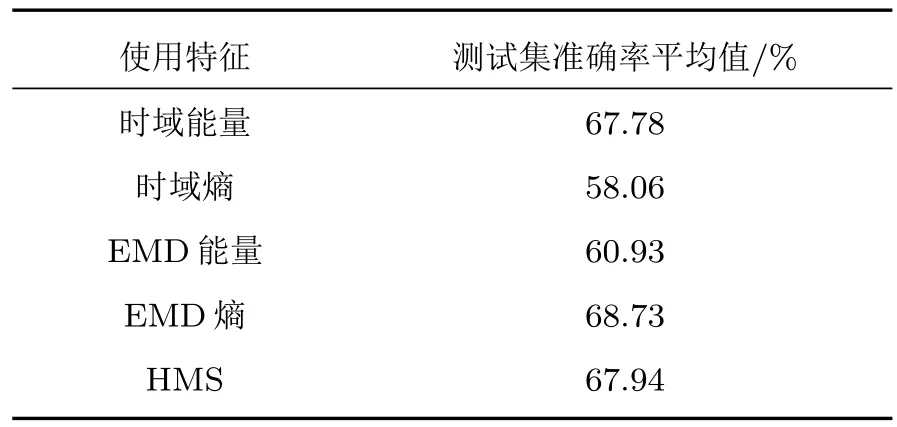
表1 5 种特征分类结果Table 1 Five feature classification results

从表1 中可以看出，在本文所使用的数据集中，5 种特征中最高的准确率为EMD 熵特征，达到了68.71%。进行EMD 后使用熵作为特征的准确率提升较高，而使用能量作为特征的准确率则有所下降。在进行实验前无法确定最优的特征提取方式，需要根据分类结果对特征向量进行设计以获取最佳特征。

2.3.2 基于NMF的分类过程

使用NMF 进行特征提取时，除字典原子个数外，还需要考虑距离度量函数的选取。本文比较了欧几里得距离(β=2)、广义K-L 散度(β=1)和IS散度(β=0)三种距离度量函数下不同字典原子个数的分类结果。分别采用SVM与CNN作为分类器，在相同条件下进行100 次分类实验，取分类准确率的平均值作为最终结果，实验结果如图7 所示。3 种距离度量函数下，在验证集上平均准确率的最大值见表2。

表2 不同距离度量函数下的分类结果Table 2 Classification results under different distance measurement functions(单位: %)

图7 不同度量函数下的分类结果Fig.7 Classification results under different metric functions

图7 中绿色虚线表示训练集上的分类结果，蓝色点划线表示测试集上的分类结果，左右两侧分别为使用SVM 和CNN 的分类结果。表2 表示采用SVM 与CNN 作为分类器时，不同距离度量函数下的平均准确率最大值以及相应的字典原子数。

结合图7 与表2，在同样使用NMF 方法作为特征输入的情况下，使用SVM 作为分类器的效果好于LeNet 的分类结果，其平均准确率的最大值在β=1、d=1 时取得，即距离度量函数选取为广义K-L散度、字典原子数选取为1的情形。在不同的度量函数下，训练集上的分类准确率随字典原子个数的增加而增加，但是在测试集上，分类准确率随字典原子个数增加呈下降趋势。这是由于原始信号中实际上包含了目标次声信号与噪声成分，而次声信号的频率低、频带窄，目标信号与噪声信号的频带混合严重[7]。当字典原子数较低时，其取值主要由目标信号决定；而当字典原子数较高时，其取值同时受到噪声影响。因此当较高维度的特征向量输入分类器后，产生了过拟合现象，识别准确率下降。对于CNN 来说，其训练集上的准确率较高，但在测试集上效果并不好，平均准确率均在70%以下，这说明对于小样本的次声信号识别分类任务而言，采用较深度的复杂模型并不是一个理想的选择，其效果差于SVM分类器。

2.3.3 实验结果分析

两组实验在测试集上的分类结果对比如图8所示，图中增加了采用一维CNN 对HMS 特征进行分类的结果。从图8 中可以看出，基于HMS 的方法虽然提高了时频分析的分辨能力，但其特征提取的方式较为直接，采用幅值相加的方式将全部分量值降为一维信号，对于原始信号来说有较多的信息损失，因此其识别的准确率并不高。在测试集上，采用NMF-SVM 进行分类的准确率最高，并且在字典原子数较低时即取得了较好的结果。

图8 两组实验分类结果对比Fig.8 Comparison of classification results of two groups of experiments

结果表明，对于次声分类这一小样本分类任务而言，采用过高维度的特征向量或过深的网络模型进行分类效果欠佳，很容易受到训练模型过拟合的影响，因此应该采用较低维的特征向量与浅层的分类模型，以提高泛化能力，获得更好的分类性能。

3 结论

对于小样本的识别分类任务，其关键问题在于特征向量的设计。本文以严格标定的数据集为基础，针对爆炸、地震、闪电和再入这4类次声信号的识别分类问题，引入了NMF 对次声信号进行特征提取，并分别使用SVM 与CNN 作为训练模型进行分类。实验结果表明，NMF-SVM 在测试集上的平均准确率可以达到83.13%，在当前数据集上获得了最佳的性能，是一种适用于次声信号识别分类的方法。