有源降噪头靠中一种分布式虚拟传声器优化方法

张锦惠 张芳杰 徐 健 郑成诗 李晓东

(1 中国科学院噪声与振动重点实验室(声学研究所) 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

工业发展在带来便捷生活的同时，也产生了大量的噪声。如今，噪声的防护越来越成为人们关注的话题。噪声会影响人们的情绪、休息与睡眠，长期暴露在高强度的噪声条件下更会对人体产生不可逆的损伤[1]。有源噪声控制(Active noise control,ANC)在控制低频噪声时具有体积小、质量轻、控制效果好的优势，受到了工业界与学者们的广泛关注[2−3]。

ANC通过引入次级声源，在目标位置产生与初级噪声幅度相同、相位相反的声音，通过声波的叠加原理，对初级噪声进行有效的控制。根据控制的目标区域，ANC 可以分为全局ANC 与局部ANC。全局ANC 旨在控制整体系统的能量输出，在降低螺旋桨飞机噪声和汽车发动机噪声上已经取得了较好的应用[4−5]。但是，控制整个空间的声场通常需要数量较多的次级扬声器与传声器，从而增加了系统实现的成本。同时，很多条件下，控制整个空间的声场是没有必要的，因此，在一些场景下，局部ANC代替了全局ANC，降低了系统的成本。有源降噪耳机是局部ANC 中最成功的应用，并且已经广泛应用于头戴式耳机以及真无线立体声蓝牙耳机的降噪中，在实际应用中，佩戴的舒适性以及堵耳效应影响了一部分使用者的使用体验[6]。有源降噪头靠能够在开放空间下在目标位置产生降噪效果，从而解放使用者的双耳[7]。有源降噪头靠已经在汽车、飞机机舱以及核磁共振舱室等应用场景下均取得了一定的进展[8−9]。

有源降噪头靠系统能够产生降噪区域的大小是系统设计中必须考虑的问题，通常定义降噪量在10 dB 以上的区域称为静音区(Zone of queit,ZoQ)。Elliott 等[10]研究表明，在扩散场环境下，单通道ANC 系统在目标位置能够产生的静音区大小约为噪声波长的1/10，这也为后面有源降噪头靠系统的设计提供了理论指导。然而，随着频率的升高，系统产生的静音区大小显著降低，人头的轻微移动就可以使得人耳处于静音区外，甚至还会感受到噪声的抬升。为了解决这一问题，虚拟传感技术逐渐受到人们的关注。虚拟传声器布置(Virtual microphone arrangement,VMA)技术最早被提出[11]，其通过假定传声器与目标位置处初级声场的一致性，将传声器处的控制效果移动至目标位置，但是仅在低频效果显著。远程虚拟传声器技术(Remote microphone technique,RMT)[12]和辅助滤波虚拟传声器(Auxiliary-filter-based virtual sensing,AFVS)[13]技术通过增加离线建模阶段，对初级噪声场进行建模，从而提升了虚拟传声器算法的降噪性能。研究表明，AF-VS 算法对初级噪声频谱的变化更敏感，而RMT 算法对通路的变化更敏感[14]，因此，RMT 算法更适合应用在噪声种类变化的有源降噪头靠系统中。然而，人头的移动会影响RMT算法的降噪性能，一种解决方案是针对人头移动进行定位，并且在每个位置都对算法进行重新迭代收敛[15]。为了实现更好的降噪性能，RMT 算法通常采用多通道结构，并且采用多通道滤波参考信号最小均方误差(Multichannel filtered-reference least mean square error,MFXLMS)算法自适应更新控制滤波器。由于次级通路之间的耦合效应，不同位置处的算法收敛性能不同，针对每个位置分别优化的滤波器的多通道远程虚拟传声器技术(Multichannel remote microphone technique,MRMT)会存在收敛性能下降的问题。针对MFXLMS 算法收敛性能的问题，Bai等[16]提出一种基于特征值分解与奇异值分解的解耦多通道算法，于光喜[17]也提出一种利用辅助次级声源的解耦的算法。这些算法提高了系统的收敛速度，但是并没有降低系统的运算复杂度。采用分布式更新能够有效地降低系统的计算复杂度，但是分布式MFXLMS 算法的收敛性能不能够得到有效的保证[18]。An 等[19]提出了一种次级通路优化算法，能够保证分布式系统的稳定性，Zhang 等[18]也提出一种次级通路寻优算法，同样保证了系统的收敛性能。

然而，上述算法均未考虑虚拟传感策略下算法的联合优化问题，为了解决上述问题，本文提出一种分布式远程虚拟传声器技术优化方法。通过重新设计MRMT 算法的离线优化过程，在限制虚拟次级通路矩阵做对角化的同时，对观测传递函数矩阵进行联合寻优，并且提出一种采用延迟FXLMS 算法的自适应分布式远程虚拟传声器更新算法。有源降噪头靠上的实验结果表明，所提算法在保证收敛性能的同时，能有效够降低算法的运算复杂度，并且提升算法的收敛速度。

1 信号模型

1.1 频域信号模型

图1 为多通道远程虚拟传声器技术示意图[20]，这里的信号模型为频域信号模型，为了表示方便，在不产生歧义的情况下，频率符号均省略。假设初级噪声场由N个初级声源产生，初级声场强度表示为v=[v1,...,vN]T，其中上标T 表示转置，而vn为第n个初级声源的声源强度。系统有I个参考传声器，采集到的参考信号可以表示为x=[x1,···,xI]T，而初级噪声源至参考传声器的传递函数矩阵可以表示为R ∈CI×N，其中CI×N为I×N阶的复数矩阵。系统有P个物理传声器和Q个虚拟传声器，其中，物理传声器为系统真实应用场景下使用的传声器，而虚拟传声器处为实际的控制点。初级声场在物理传声器处与虚拟传声器处的初级噪声可分别表示为dm=[dm,1,···,dm,P]T和dv=[dv,1,···,dv,Q]T，初级声场与声源强度的关系分别为

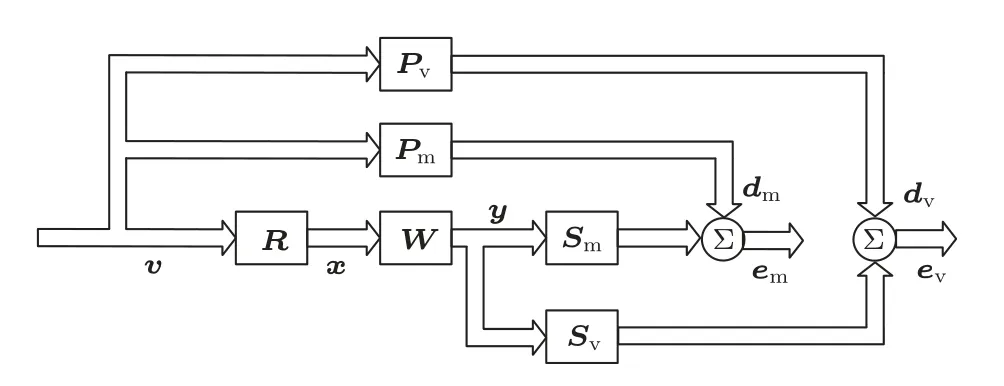
图1 多通道远程虚拟传感技术频域模型示意图Fig.1 Diagram of the multichannel remote microphone technique

其中，Pm∈CP×N和Pv∈CQ×N分别为初级噪声源至物理传声器与虚拟传声器处的传递函数矩阵。

假设系统有J个次级声源，用来产生控制虚拟传声器处的初级声场的反向信号。次级声源的输出向量可以表示为y=[y1,···,yJ]T，控制信号由参考信号经过控制矩阵W ∈CJ×I得到：

控制过后，物理传声器与虚拟传声器处的误差信号分别为

其中，Sm∈CP×J和Sv∈CQ×J分别为次级声源至物理传声器与虚拟传声器处的传递函数矩阵。

在实际控制中，由于无法获得虚拟传声器采集到的信号，需要对虚拟传声器处的误差信号进行估计，从而对目标位置进行有效的控制。MRMT 算法首先估计虚拟传声器处的初级声场dv：

其中，O ∈CQ×P为观测传递函数矩阵，通过最小化tr[E{(dv−Odm)(dv−Odm)H}]可以得到最优的观测传递函数为

其中，上标H 表示共轭转置，tr[·]表示矩阵的迹，E{·}代表期望。

由于物理传声器处的初级噪声dm无法直接测量得到，物理传声器处的初级噪声需通过物理传声器处的误差信号与系统的输出信号估计得到：

1.2 收敛性能分析

MRMT 算法的收敛性主要受到两方面的影响，其一是参考信号之间的相关性，其二是次级通路传递函数之间的耦合效应。本小节首先假设信号为单频信号，采用文献[15]中的分析方式，对远程虚拟传声器算法的收敛性能进行分析，频域多通道ANC的更新公式为

假设最优的输出信号为y(∞)，将误差信号生成带入式(8)可得

可得到系统最优滤波器为

将式(8)两端减去最优滤波器可以得到

这里假设物理次级通路矩阵的估计不存在误差，从式(11)中可以得到，算法收敛的必要条件为

其中，λj为特征矩阵的第j个特征值，可以看出，当物理次级通路矩阵的估计不存在误差时，矩阵为正定矩阵，因此收敛条件一定能够得到满足。而算法的收敛速度取决于矩阵的条件数，即最大特征值与最小特征值的比值。

如果直接采用分布式的远程虚拟传声器算法(Distributed remote microphone technique,DRMT)[3]，其更新公式为

2 算法原理

2.1 所提算法

在算法的控制阶段，系统通过最小化估计误差信号的均方误差以实现最优的控制效果，此时，估计误差信号的均方误差可以表示为

其中，Svv为初级噪声源信号源强的自相关矩阵。令代价函数对控制滤波器W的导数为0，即：

可以得到最优的控制滤波器为

假设系统可以达到最优控制效果，则虚拟传声器处真实的误差信号为

由于虚拟传声器算法的最终效果，是最小化系统达到最优控制效果后真实虚拟传声器处误差信号的均方误差，将式(17)得到的最优滤波器带入式(18)，可以得到真实目标位置的均方误差为

为了得到在分布式更新算法下最优的观测传递函数，将上面的代价函数对求偏导，并且令导数为0：

得到新的最优观测传递函数为

2.2 算法时域实现

本节首先介绍MRMT 算法的具体实现，其可以分为两个步骤：第一步为训练阶段，在训练阶段，需将虚拟传声器安装在所控制的目标位置，然后分别测量得到物理次级通路以及虚拟次级通路的估计值与。之后，在初级噪声场条件下测量得到物理传声器与虚拟传声器处的初级噪声信号dm与dv，进而测量得到物理主通路与虚拟主通路Pm与Pv，通过式(5)求出最优的观测传递函数Oopt。第二步为控制阶段，控制阶段通过最小化估计得到的虚拟传声器处的误差信号的均方误差，以求得最优的控制滤波器。通常，第二阶段采用MFXLMS 算法自适应地寻找最优的滤波器。在控制阶段，系统的输入只有参考信号以及物理传声器处的误差信号，虚拟传声器被拆除，从而不影响头靠系统的正常使用。若系统n时刻的输出信号表示为y(n)=[y1(n),···,yJ(n)]T，其中yj(n)为第j个次级扬声器的输出信号，则有

其中，xi(n)=[xi(n),···,xi(n−L+1)]T为第i个参考信号抽头系数向量，滤波器的阶数为L，wji(n)=[wji,0(n),···,wji,L−1(n)]T为第i个参考信号到第j个输出信号的控制滤波器向量。

第n时刻估计得到的物理传声器处的初级信号为

其中，em,p(n)为第n时刻采集到的物理传声器处的误差信号，sm,pj为第j个次级声源到第p个物理传声器处的次级通路单位冲激响应，yj(n)=[yj(n),···,yj(n−M+1)]T为输出信号抽头系数向量，阶数为M。则第q个虚拟传声器处的初级声场估计值为

假设单位冲激响应opq在这K个频点上的频率响应Opq可以表示为

其中，F为频率响应转移矩阵，定义为

通过最小化Opq与opq之间的均方误差，可以求出最优的单位冲激响应为

第q个虚拟传声器处误差信号的估计值可以通过式(28)求得：

其中，sv,qj为第j个次级声源到第q个物理传声器处的次级通路单位冲激响应，滤波器的更新公式为

其中，rijq(n)=[rijq(n),···,rijq(n−L+1)]T为滤波参考信号抽头向量，µ为更新步长，滤波参考信号可以通过式(30)计算得到：

为了方便表示，一个结构为1×2×2×2 的自适应远程虚拟传声器技术算法框图如图2 所示，其中1×2×2×2 代表系统有一个参考传声器，两个次级扬声器，两个物理传声器以及两个虚拟传声器。

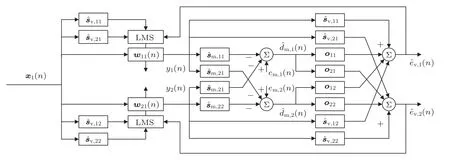
图2 1×2×2×2 远程虚拟传声器技术框图Fig.2 Diagram of the adaptive multichannel remote microphone technique with 1×2×2×2 structure

其次介绍所提算法的时域实现。在算法的实现过程中，需将优化得到的观测传递函数转换为单位冲激响应，为了防止本文优化得到的观测传递函数存在非最小相位部分，需对观测传递函数人为的增加∆个采样点的延迟，假设所提算法第p个物理传声器到第q个虚拟传声器处观测通路的单位冲激响应为，阶数为L，假设在K个频点上面得到的最优观测传递函数向量为。将最优观测传递函数向量延迟∆可以得到延迟过后的传递函数向量为

其中，fs为采样率，单位冲激响应在这K个频点上的频率响应可以表示为

注意到此时得到的单位冲激响应相比最优的传递函数会有∆个采样点的延迟，因此需要采用延迟的虚拟传声器算法进行更新[21]。此时估计得到的误差为

所提算法的更新公式为

其余的计算与MRMT 算法保持一致。本文称所提算法为优化的分布式远程虚拟传声器算法(Optimized distributed multichannel remote microphone technique,ODMRMT)，该文所提算法以及传统算法如表1 所示。注意到所提算法更新会有∆个采样点的延迟，这会影响算法的收敛性能，但是可以将优化得到的观测传递函数中非最小相位部分进行建模，从而提高算法的稳态性能。所提算法的流程图如图3 所示，对比图2 和图3 可以发现，所提算法在生成误差信号以及滤波器更新的过程中，均消除了次级通路的耦合现象，从而降低了算法的运算复杂度，并且提升了收敛速度。

表1 3 种算法流程图Table 1 Pseudo code for three different algorithms

图3 1×2×2×2 分布式远程虚拟传声器技术框图Fig.3 Diagram of the distributed adaptive multichannel remote microphone technique with 1×2×2×2 structure

所提ODMRMT 算法与MRMT 算法以及DRMT 算法的复杂度对比如表2 所示。从表2 可以看出，相比MRMT 算法，所提算法在生成误差信号时减少了(Q−1)JM次乘加运算，计算滤波误差信号时减少了(Q−1)JIM次乘加运算，更新滤波器时均减少了(Q−1)JIL次乘加运算，而相比于DRMT 算法，所提算法在生成误差信号时也降低了(Q−1)JM次乘加运算。因此，所提算法能够有效降低算法的运算复杂度。为了更好地分析所提算法在降低运算复杂度方面的优势，将所提算法与MRMT算法以及DRMT算法的运算复杂度绘制为如图4 所示曲线。其中图4(a)假设系统的次级声源、物理传声器、虚拟传声器的个数均为2 个，以此分析这种条件下滤波器缓存长度对算法运算复杂度的影响。图4(b) 假设滤波器的阶数为256 阶，并且假设次级声源、物理传声器、虚拟传声器的个数相同，分析这种条件下系统通道个数对运算复杂度的影响。由图中可知，当通道数固定时，所提算法拥有最低的运算复杂度，且随着阶数增加，对运算复杂度的降低更明显。而当滤波器阶数固定时，所提算法运算复杂度随着通道数的上升相比于MRMT 算法以及DMRMT 更缓慢，且运算复杂度更低。

表2 不同算法计算复杂度对比Table 2 Compare of Computational complexity of different algorithms

图4 不同算法运算复杂度对比Fig.4 Comparation of the computational complexity of different algorithms

3 实验结果和分析

3.1 实验设置

本文通过一个有源降噪头枕系统对所提算法进行实验验证，实验系统设置如图5 所示。有源降噪头枕布置在中国科学院声学研究所测听室内，房间尺寸约为4.22 m×4.05 m×3.28 m，本底噪声平均值为14.8 dB(A)，混响时间约为0.3 s。有源降噪头枕系统由一个参考传声器、两个物理传声器、两个虚拟传声器、两对固定在头枕两边的两寸次级扬声器、控制器和信号调理器组成。其中，控制器为TI 公司的TMS320C6678 数字信号处理芯片，参考传声器与物理传声器均为驻极体传声器，通过前置放大器、抗混叠滤波器、模数转换器(ADC)接入控制系统，而输出信号经过重构滤波器、数模转换器(DAC)以及功率放大器接入次级扬声器。虚拟传声器为B&K 公司人工头内部传声器，用来监测算法的实际控制效果。实验采用的抗混叠滤波器和重构滤波器均为截至频率为700 Hz 的巴特沃斯低通滤波器，通过模拟电路实现。系统的采样率设置为4000 Hz。采用单耳处的归一化均方误差(Normalized mean square error,NMSE)作为算法的评价指标，归一化均方误差定义为

图5 实验系统示意图以及有源降噪头枕俯视图Fig.5 setup of the experiment and the planform of the active noise cancelling pillow

其中，期望可以采用下面平滑的方式进行计算：

其中，β为平滑因子，取值为0∼1之间，典型取值为0.001∼0.01。

3.2 传递函数测量

为了实现本文所提算法的优化过程，需要先对系统的主通路、物理次级通路以及虚拟次级通路进行测量，本节采用白噪声生成法对系统的传递函数进行测量。选取通路的滤波器阶数为200 阶，本文分别测量了人头位于中心位置以及人头靠近头枕右侧传声器处时的通路响应。当人工头处在中心位置时测量得到的传递函数如图6 所示。从图中可以看出，相对于主通路，次级通路的频响更加平坦，相位响应接近于线性相位。之后，可以通过所提方法求出最优的观测滤波器。

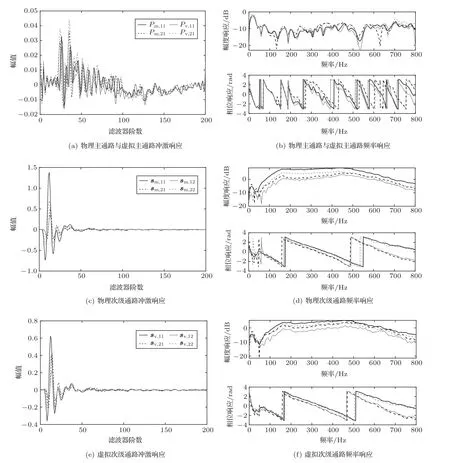
图6 传递函数测量结果Fig.6 Measurement results of plant models

3.3 实验结果

3.3.1 单频噪声条件下的ANC实验

本节首先对初级噪声源为谐频噪声条件下所提算法的性能进行探究，并且与传统的MRMT 算法以及DMRMT算法进行比较，本文所选谐频噪声的频率为300 Hz。实验所采用的为周期噪声，因此在使用式(28)生成观测通路的冲激响应时仅选取300 Hz 处的频响，并且不需要额外引入新的延迟操作。在人头在中间位置与人头靠近头枕右侧位置分别优化出各自位置最优的观测传递函数，并且分别在两个位置采用3种算法进行实验，3种算法所用的更新步长均为0.001，平滑因子选取为0.001。得到的结果如图7所示，从图7(a)中可以看出，当人头位于中心位置时，3 种算法的收敛速度相当，这是由于此时特征矩阵的散度本身就较小，因此，所提算法的收敛速度仅略优于传统的MRMT 算法与DMRMT算法。而当人头靠近一侧时，此时系统的特征矩阵散度增大，传统的MRMT 算法与DMRMT 算法的收敛速度均出现了下降，尤其是左耳处的收敛十分缓慢，而采用了本文所提算法，在左右耳处均能达到更优的收敛性能。

图7 窄带噪声头枕实验结果Fig.7 Experiment results of the active noise cancelling pillow with narrowband primary noise

3.3.2 宽带噪声条件下的ANC实验

实际应用场景宽带噪声极其普遍，本节采用宽带噪声对所提算法在有源降噪头枕上进行实验验证。本文分别采用两种宽带噪声，一种为带通的白噪声，通过将白噪声经过一个通带为100∼500 Hz的带通滤波器生成，另一种噪声为实录的汽车噪声。

本节在头枕的中心位置进行实验，本文在100∼500 Hz 之间、间隔10 Hz 选取频响对观测传递函数进行优化，同时，由于噪声为自相关较差的宽带信号，观测通路的非最小相位部分会影响算法的稳态性能，本节选取时延为20 个采样点。3 种算法的步长选取均为0.05，平滑因子选取为0.001。

从实验结果(图8)可以看出，不管是带通白噪声还是实录汽车噪声，所提算法均能够实现最优的收敛性能，同时达到和传统算法一致的稳态误差。可以看出，对次级通路矩阵做对角化限制，使得所提ODMRMT 算法在估计误差传声器的误差信号时，虚拟系统的等效次级通路不存在耦合现象，从而提升了算法的收敛速度，而对观测传递函数矩阵进行联合寻优则保证了系统在真实误差传声器处的降噪性能。注意到在头枕实验条件下，DMRMT算法均没有出现发散的情况，但是从式(17)可以看出，DMRMT 算法的算法收敛条件并不能够保证一定满足。

图8 宽带噪声头枕实验结果Fig.8 Experiment results of the active noise cancelling pillow with broadband primary noise

4 结论

为了解决多通道远程虚拟传声器算法在实现过程中运算复杂度高、收敛速度慢的问题，本文提出一种分布式远程虚拟传声器技术优化方法。通过重新设计离线优化过程，在限制虚拟次级通路矩阵做对角化的同时，对观测传递函数矩阵进行联合寻优，得到在分布式更新条件下的最优观测传递函数，并且通过延迟FXLMS 算法自适应对系统进行迭代。在有源降噪头枕上的实验结果表明，所提算法能够降低算法的运算复杂度，并且提升算法的收敛速度。