游戏活动如何促进数学理解

摘要：为探索学生在游戏活动实现数学理解的历程 ，开展了主题为 “学生如何通过游戏活动实现数学理解 ”的课堂观察 ，发现实际教学中存在缺乏层次性的问题引领、缺少操作后的思辨交流等问题。对此 ，提出教学建议 ：游戏活动的设计应符合学生的认知需求 ，具有一定的挑战性 ;游戏活动中应提供充足的操作时空 ，引导自主探究 ;游戏活动后应有效组织评价 ，深化数学理解。

关键词 ：小学数学 ;游戏教学 ;课堂观察 ;余数

游戏在儿童认知发展中具有重要作用。将游戏与数学教学活动相结合 ，不仅能为儿童在自发探索条件下提供大量的尝试机会 ，还能降低儿童对结果的期望和对失败的畏惧，促进数学理解的萌发、跃迁与深化。为探索学生在游戏活动中实现数学理解的历程 ，我们开展了主题为 “学生如何通过游戏活动实现数学理解 ”的课堂观察 ，用的是自编内容 “余数的妙用 ”，置于苏教版小学数学二年级下册《有余数的除法》单元例 3教学后。通过探索若干图形中的周期规律 ，引导学生在观察、描述、表征规律的基础上 ，理解除法算式中余数的含义 ，建立 “形”与“数”、“数”和“算”的联系。《余数的妙用》课堂观察报告如下 ：一、观察内容与量表设计本次教学 ，教师设计了三个游戏活动 ：

（1）“整齐不整齐 ”。观察三组图形排列 ，每组有10个图形 ，一组为有规律的图形 ，两组为无规律的图形。通过观察 ，感受规律中的周期现象。（ 2）“帮图形排排队 ”。通过画图、数数、列式等多种方法 ，发现规律中的第 N个图形。通过多种方法对比 ，提炼方法 ，建立除法算式与找规律的联系。（ 3）“一起动脑筋 ”。

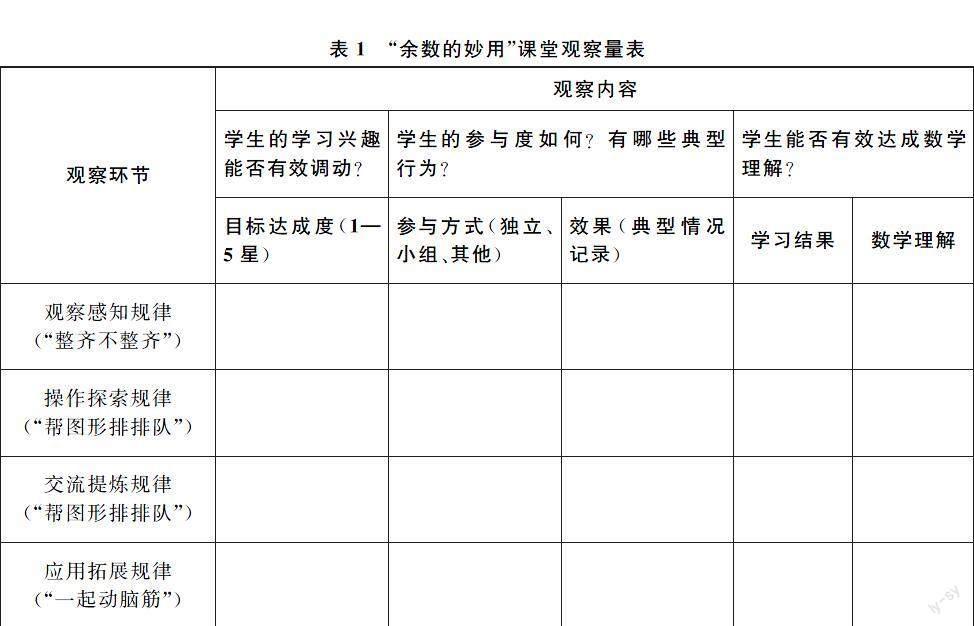
运用题组及变式练习 ，将数学与生活联系起来。通过观察前的讨论 ，我们认为 ，课堂教学可以解构成四个观察环节 ：观察感知规律 （“整齐不整齐 ”）、操作探索规律 （“帮图形排排队 ”）、交流提炼规律 （“帮图形排排队 ”）、应用拓展规律 （“一起动脑筋 ”）。

本次课堂观察的主要内容是 ：（1）游戏活动中 ，学生的学习兴趣能否有效调动 ？ （2）学生的参与度如何 ？有哪些典型行为 ？ （3）学生能否有效达成数学理解 ？

课题组除了使用常规的课堂现场观察技术，如选择性地逐字记录、轶事记录外 ，还利用了自编的课堂观察量表 （详见表 1），切片式地记录教学任务与学生行为。

二、观察要点与记录分析

课题组邀请 L老师执教 ，3位教师组成观察小组 ，分别根据不同的观察需要 ，选择合适的位置 ，同时围绕三个观察要点进行课堂观察、捕捉和记录。座位情况如图 1所示 ，其中，数字 1、2、3为3位观察教师的位置 ;★表示学习优秀的学生 ，●表示课堂活跃的学生。

（一）学生的学习兴趣能否有效调动 ？

在第一个观察环节中 ，有 4位学生没有积极投入学习 （3位学生玩尺子或橡皮 ，1位学生穿脱外套）。观察教师认为 ，部分学生可能对该游戏兴趣不大 ，因此表现得不够积极。

在第二个观察环节中 ，第一次操作时 ，绝大部分学生都能通过操作、画图、画圈、数数进行自主探索 ，极个别学生一开始没有任何举动。观察教师认为 ，这些学生可能在独立思考 ，对问题一时之间没有头绪。

在第三个观察环节中 ，L老师采用一问一答的形式 ，从观察、分组到列式解答 ，继而分析余数所对应的物体 ，逐一回顾解决此类问题的方法与步骤。在此过程中 ，个别用画图法没有完成 32个图形的学生表现得不够积极 ，有1位学生在其他人归纳总结的过程中仍然尝试偷偷完成画图。在 2号观察教师旁有 2位学生并没有写出除法算式 ，在师生问答环节也没有举手发言。观察教师认为 ，思考的时间有些短 ，部分学生还存在疑惑。

在第四个观察环节中 ，对于不同的练习题目 ，学生的表现迥然。当 L老师出示一行棋子 ，并以三黑二白的排列规律逐渐展示时 ，学生对于寻找规律和解答 ，积极性较高。当 L老师出示 “小雨喜欢练书法 ，他把 ‘我爱伟大的祖国 这句话反复书写 ，第 40个字是什么字 ？”时，有不少学生仍然用画圆圈的方法解决。但由于无法像上一题一样仅用黑白圆圈表示不同的文字 ，感到无法解决 ，表现出注意力分散。

（二 ）学生的参与度如何 ？有哪些典型行为 ？

在第一个观察环节中 ，学生在 L老师的引导下积极主动地观察三组水果图形 ，快速找到了含有周期规律的两组图形。多名发言的学生能用自己的语言描述找到的周期 ，并获得其他学生的认可。

在第二个观察环节中 ，L老师出示例题并提出观察要求 ，但仅邀请了 1位学生回答。在利用画图找到第 17个图形的操作中 ，给予学生的任务指向明确 ，并且留给学生充分的独立思考的时间 ，学生表现出较高的参与度。在2号观察教师附近的学生 ，均以独立参与的方式积极进行游戏。绝大部分学生根据教师的指令将所有图形一一画出 ，并找到第 17個图形 ;部分学生在画出 17个图形后 ，会把规律用圆圈框出 ;个别学生在观察后直接列出除法算式。此环节中 ，学生参与热情高 ，发言意愿强。整节课 ，学生参与活动的方式均为独立解答 ，集体交流。

在第三个观察环节中 ，L老师邀请学生回答如何解决周期问题。第一个学生直接回答用除法计算 ;部分学生在他人发言的同时 ，仍然停留在自我表达的层面上 ，并未随着他人的发言而展开深入思考 ，仍然举手尝试回答不同的方法 ;个别学生停留在未完成的操作环节 ，没有参与课堂交流与互动。

在第四个观察环节中 ，举手发言的学生人数逐渐减少 ，发言权逐渐聚焦在课堂活跃的部分学生手上。观察教师认为 ，可能与部分学生以听讲代替参与的习惯有关 ，也可能是题组练习的难度加深导致部分学生仍然处于迷惑与思考状态。

以整节课为时间轴来观察 ，对于四个不同的教学环节 ，部分学生的学习热情在课堂上逐渐衰减。以第一列最后一位学生为例 ，例题的 “试算第 17个图形是什么 ”环节 ，该生能自主列出除法算式 ;L老师提问 “第 32个图形是什么 ？”时，该生快速列出正确算式，并积极举手 ;在后续的练习中 ，该生虽然每次都列出了正确算式 ，却再也没有举过手。

（ 三）学生能否有效达成数学理解 ？

从数学理解的角度来看 ，根据课堂观察我们发现 ，学生对 “周期现象中的第 N个图形是什么 ”的掌握程度并不理想。一部分学生在练习环节中仍然采用一个一个数、一组一组画的方法 ，无法有效将除法算式与图形规律对应结合。以第二列第五位学生为例 ，该生第一次画图形时 ，会圈出一组一组的规律，而到完成黑白棋子的规律习题时 ，只有画图，圈出规律的步骤已经消失。还有不少学生虽然知道应该采用除法算式 ，但对于式子真正的意义并不理解。当题目中出现非良构问题 （为了庆祝节日 ，要在长江大桥的一边挂彩灯 ，按 “红、黄、蓝、绿、紫、青”的顺序挂 50个，第35个彩灯是什么颜色 ？）时，面对多余的数据 ，学生出现迷思 ，甚至出现了 50÷6这样的算式。在师生交流时 ，有 1位学生写出了一组灯笼的颜色后 ，在其上来回数图形 ，没有参与课堂总结活动。课后 ，我们访谈了部分学生。列出 35÷7的学生表示 ，自己着急 ，数错了一组灯笼有几个 ;列出 50÷6的学生表示 ，题目中的数字太多 ，只知道用除法做 ，但用哪个数除以 6不明白。

三、启示与建议

通过课堂观察与记录整理 ，我们发现了本次教学的一些问题。游戏活动多 ，但缺乏层次性的问题引领。学生面对一环又一环的游戏 ，一直处于活动操作之中。由于缺少层次性的问题引领 ，学生对游戏之间的关联、规律与算式之间的联系思考较少。并且 ，缺少操作后的思辨交流。L老师仅在第一次找规律时 ，引导学生画图操作 ，但对于完全列举画图、画图之后用圆圈一圈、在一组规律上来回数这几种典型的操作 ，没有组织学生进行比较与讨论。这也就导致游戏活动结束后 ，产生了 “滑过现象 ”，相当一部分学生对相应知识点的数学理解仍然处于浅表层面。对此 ，我们认为 ，通过游戏活动促进学生数学理解需要注意以下几点 ：

（一）游戏活动的设计应符合学生的认知需求 ，具有一定的挑战性

早期的古典游戏理论 ，主要通过本能和进化的角度推理人们为什么要玩游戏。随着现代心理学理论的出现和完善 ，越来越多的学者注意到了游戏的价值。精神分析理论的创始人弗洛伊德从人格理论的 “本我、自我和超我 ”出发 ，阐释了游戏对人类发展的重要作用。[1]维果茨基认为 ，游戏是决定儿童发展的主导活动 ，是一种有意识、有目的的社会实践

活动 ;它的本质是社会性的 ，除了儿童创造了现实生活以外 ，游戏还是以语言和工具为中介学习人与人基本社会关系的实践场所 ;游戏可以促成儿童心理机能从低向高发展 ，如象征性游戏让儿童实现了思维符号化和抽象化的过程 ;儿童在游戏中的行为往往要略高于他的日常行为水平 ，这两者的差距形成了儿童的 “最近发展区 ”。

因此 ，设计游戏活动时 ，教师不仅要考虑教学内容 ，还要充分结合学生的已有经验和心理特征。比如 ，本课导入环节 ，教师可以采用这样的游戏活动 ：“联欢会上 ，同学们买了 50个彩色气球进行装饰。如果按照 3个红气球、2个黄气球、1个绿气球的顺序把气球串起来。你知道第 16个气球是什么颜色吗 ？”这样的游戏活动 ，显然更具有趣味性和挑战性。一方面 ，游戏来自生活情境 ，利用布置教室的现实需求 ，将数学与生活进行了有效关联。另一方面 ，游戏呈现的数学问题并非良构问题 ，具有充分的挑战性。解决这个问题 ，不仅需要学生厘清条件 ，甄别解决问题所需的条件 ，还需要学生借助表征 ，表达规律并推断，比原本教学设计中的周期图形往后依次排列更具有思维含量。这样的游戏设计 ，为儿童提供了用数学眼光观察现实世界的探究方式。儿童在游戏中 ，自然实现了思维符号化和抽象化的过程 ，建立了数学与现实世界的联系。

（二）游戏活动中应提供充足的操作时空，引导自主探究

教学中的游戏不同于普通游戏 ：游戏是途径 ，教育是目的。现代心理学认为 ，具身认知是一种有效的学习方式 ，它是环境、身体与认知的交互生成。从学习的环境来看 ，具身认知呈现的是动态开放的学习情境 ;从学习的方式来看 ，具身认知强调的是身体在学习中发挥的作用 ;从学习过程来看 ，具身认知产生的是建构生成的自我体验。[2]

因此 ，运用游戏活动开展教学时 ，教师应提供丰富的活动材料 ，组织学生进行操作感知，观察比较。比如 ，在探索第 16个气球是什么颜色时 ，教师可以将学生两两分组 ，为学生提供不同颜色的圆片、格子图、小棒、彩笔等，引导学生根据游戏要求来排一排、画一画、写一写、算一算。学生在操作的过程中 ，不断循环周期规律 ，进行身心认知。教師应给予学生充分的时空 ，使学生在不同的操作过程中 ，依据色彩、文字、符号等变化感知气球的周期规律 ，同时借助操作支持 ，达成对周期现象从经验性理解到形式化理解。

（三）游戏活动后应有效组织评价 ，深化数学理解

加涅强调 ：“学习的每一个动作 ，如果要完成 ，就需要反馈。所”以，即使教学带上了游戏特性 ，评价与反馈仍然是重要的环节。运用游戏活动开展教学时 ，教师应高度重视学生的不同行为表现 ，并及时组织评价。

比如 ，在探索第 16个气球是什么颜色时，教师可以根据观察到的不同操作 ，邀请学生代表上来讲解问题解决的思路与方法。同时 ，根据不同的操作及图示 ，引导学生观察：不同的组别在解决问题时有什么共同之处？学生可能会发现 ，不管是摆圆片还是写汉字 ，这些气球都是按照一定顺序排列的———红、红、红、黄、黄、绿，是有规律的。教师可以继续引导学生观察并思考 ：这些不同操作可以用相同的算式来表示吗 ？为什么用除法算式 ？学生在观察、比较、提炼中会逐步发现 ，要知道第 16个气球是什么颜色，需要看 16个气球中包含了几组这样的周期现象 ，然后思考余数与气球颜色的对应关系。教师应引导学生将找规律与包含除的方法进行对比 ：一组周期数量即算式中的除数 ，求某个位置其实是观察若干数量中分别包含多个组合后剩余的情况。如果学生列出含有 50的算式 ，教师可以组织二次辨析与评价。50是气球的总数 ，表示数量的意义 ;16是气球排列后产生的 ，表示次序的意义。学生结合操作经验 ，在游戏活动中辨析序数与基数的含义 ，气球的颜色与总共有 50个气球无关 ，与气球排列的次序相关 ，并产生相应的数学理解。

R.斯根普指出 ，学生在学习数学知识的过程中通常有 2种含义迥然不同的数学理解模式 ：工具性理解和关系性理解 ，更多的理解应当定位于关系性理解。[3]同样地 ，我们认为，在游戏活动中 ，数学理解并不能一蹴而就，它是一个螺旋上升、不断跃迁的过程。数学理解不仅要借助游戏中的具身操作 ，还依赖于游戏活动中的经验总结与提炼。当学生的原始认知与产生的表象经由性质认知后 ，教师应及时组织观察评述活动 ，通过师生、生生间的辨析、质疑、交流构造知识网络 ，提炼凝化 ，达成数学理解。

以游戏活动促进数学理解 ，不仅需要用层级跃迁的游戏环节来带动学生体验 ，同时也需要提供给学生充足的操作空间 ，更应重视活动后的评价组织。

参考文献 ：

[1]尚俊杰 ，裴蕾丝 .重塑学习方式 ：游戏的核心教育价值及应用前景 [J].中国电化教育，2015（5）：42.

[2]沈君 .在具身学习中发展空间观念———以“平移与旋转 ”一课的教学为例 [J].数学学习与研究 ，2021（17）：78 79.

[3]马复 .试论数学理解的两种类型 ———从 R.斯根普的工作谈起 [J].数学教育学报 ， 2001（3）：50 51.

（沈君，江苏省江阴市花园实验小学。）