一种三回路过载自动驾驶仪设计方法

陈中祥,韦汉林,任 韦,2

1. 江南机电设计研究所,贵阳 550009 2. 哈尔滨工业大学航天学院,哈尔滨 150001

0 引言

三回路过载自动驾驶仪结构因其具有良好的系统稳定性、快速性和鲁棒性[1],广泛应用于战术导弹领域[2]。常用的三回路过载驾驶仪包括:伪攻角反馈驾驶仪和经典的Raytheon三回路驾驶仪。其中,经典的Raytheon三回路驾驶仪是由Raytheon公司为应对其雷达导引头寻的制导回路设计而首次提出,因该结构不受气动变化的影响,对高频噪声有较强的滤波能力,并可以减低雷达导引头天线罩折射误差斜率对制导回路的影响,而得到广泛的应用。文献[3]指出了该经典三回路自动驾驶仪频域设计方法,通过指定控制系统期望的时间常数τ,阻尼ζ,开环截止频率ωCR,求解闭环系统二阶固有频率,实现对闭环系统的极点配置,但是,其设计过程未考虑到控制系统期望指标的工程约束条件,导致当系统开环截止频率ωCR不满足远大于弹体固有频率时,其设计结果在工程实际中存在较大误差。文献[4]在文献[3]的基础上,提出的极点配置设计方法考虑了舵机动态特性等工程实际约束的影响,通过系统参数寻优实现了考虑舵机动态特性的极点精确配置,但是其设计过程未考虑系统开环截止频率及最大舵偏角速度约束。文献[5]提出了经典三回路过载自动驾驶仪设计不应以自振频率为主要设计指标,而应以系统开环截止频率约束为主要设计指标的思想,并给出了相关设计方法,但是其设计过程仍未能充分考虑最大舵偏角速度约束。

而伪攻角反馈增稳回路因采用伪攻角反馈,可以消除经典三回路驾驶仪的静差,同时能保留较好的时域、频域响应特性及鲁棒性能,因此,在战术导弹上得到广泛的应用[6]。文献[7]指出了以系统开环截止频率为主要设计指标的驾驶仪设计方法,该方法的实际设计结果与期望指标一致性较好,但是其设计过程未考虑相位裕度、舵偏角速度等相关工程约束。文献[8-9]指出了伪攻角反馈自动驾驶仪的极点配置设计方法,通过建立控制增益与闭环极点、开环截止频率的解析关系式,考虑系统高频部件约束、舵偏角速度约束及相位裕度约束,并基于Butterworth滤波器提出“共圆准则”,增加在同样开环截止频率及阻尼条件下,最小化闭环系统等效时间常数实现伪攻角反馈形式下,考虑开环截止频率约束的极点配置方法。其设计的期望截止频率与实际截止频率差异较小,但是因部分弹体模型采用了近似性计算导致相位裕度具有一定的保守性。

综上,当前三回路过载自动驾驶仪设计中,对于如何在充分考虑工程实际中舵偏角速度、开环截止频率、相位裕度以及高频部件等的约束条件下,完成参数的最优化、精确化设计仍需要开展相关研究。本文首先从常用的三回路过载驾驶仪的模型出发,统一给出系统开环传递函数与闭环系统特征方程的关系,然后依据闭环传递函数确定系统控制增益与闭环极点、开环截止频率的关系,通过引入舵偏角速度约束、开环截止频率、稳定裕度指标约束,高频部件约束,进而给出最小化闭环系统等效时间常数的目标函数,形成典型的约束条件下参数寻优范式,通过求解系统最优解,实现系统开环截止频率、相位裕度的精确设计,形成一种可工程化的设计方法。

1 弹体纵向运动方程

导弹是一个时变、非线性的弹性结构体,通常将战术导弹视为刚体。利用小扰动线性化方法,对弹体纵向运动方程进行简化,得到便于控制系统设计用的线性化模型。常用的线性化方程表示如下:

(1)

由此,可得如下传递函数:

(2)

(3)

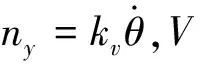
2 三回路过载驾驶仪结构

常用的伪攻角反馈三回路过载驾驶仪结构[9]如图1所示,经典三回路过载驾驶仪结构[9]如图2所示。图1中:KAC,Kα和Kg为伪攻角反馈结构中的反馈系数;KDC,KA,ωi和KR为经典三回路结构中的反馈系数。在伪攻角反馈结构中,通常取A4=a4-a2a5/a3。图2中:c表示加速度计在弹上的安装位置,正的c表示安装在导弹质心之前。

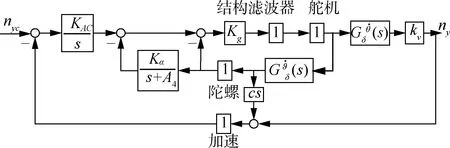
图1 伪攻角反馈三回路过载驾驶仪结构图

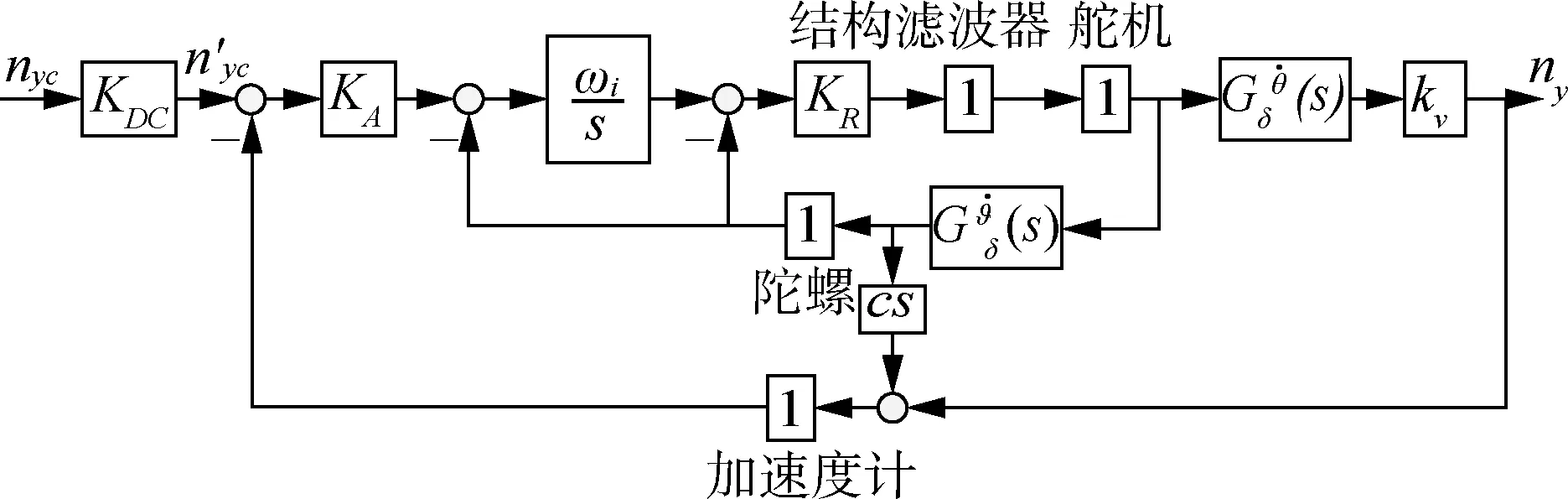
图2 经典三回路过载驾驶仪结构图

弹体气动参数的不确定性是整个控制系统中最严重的环节,通常分析舵机断开处的开环传递函数[10]。当忽略图中舵机、速率陀螺、加速度计及结构滤波器的高阶动态,对于伪攻角反馈结构,可得如下形式的开环传递函数(不考虑c):

(4)

式中:

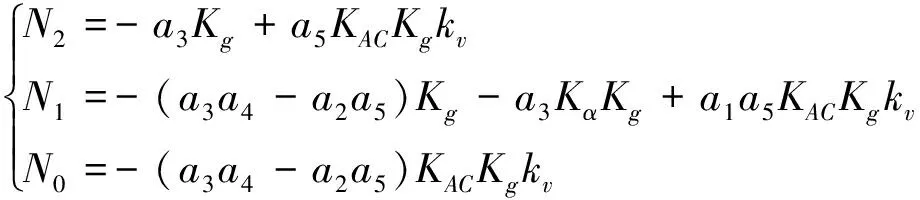
(5)

同理,对于经典三回路结构,可得如下形式的开环传递函数(不考虑c):

(6)

式中:

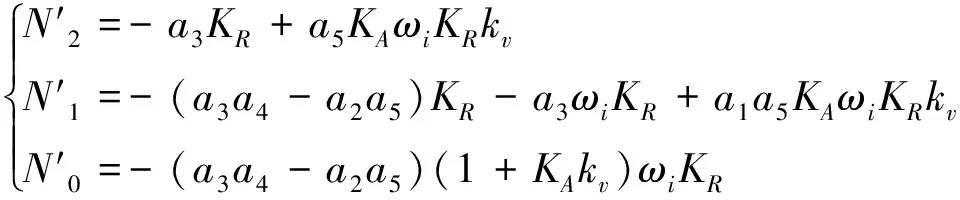
(7)

对比两种结构形式的开环传递函数式(4)和(6),具有相同的形式。

定义:A1=a1+a4,A2=a2+a1a4;对于伪攻角反馈,可以求解从指令到过载的闭环传递函数:

(8)

显然,其闭环传递函数稳定增益恒为1,说明伪攻角反馈结构对过载指令是一阶无静差系统[9]。

同理,对于经典三回路,可以求解从指令到过载的闭环传递函数:

(9)

在图2结构中,设置前置补偿系数[11]KDC能保证指令到过载的稳态传递系数为1。这是解决经典三回路对指令有静差系统的补偿措施。

3 三回路过载驾驶仪闭环特征方程与开环传递函数

对比式(8)和(9)可知,伪攻角反馈结构与经典三回路结构具有相同结构的闭环传递函数。当两个结构中闭环传递函数相同时,式(5)和(7)应满足:N2=N2′、N1=N1′、N0=N0′。

假设闭环传递函数的的特征方程为:

(10)

对于伪攻角反馈结构:

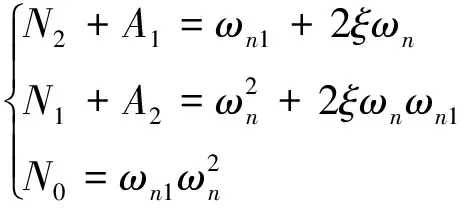
(11)

对于经典三回路结构可以推导,其结构形式完全相同,只是将式(11)中的Ni换为Ni′,i=0,1,2。

对于伪攻角反馈结构,利用闭环特征方程的参数,确定其控制回路增益,KAC,Kα和Kg如式(12)。

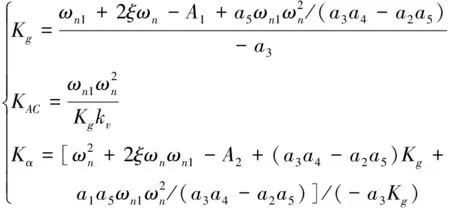
(12)

同理,对于经典三回路结构,其控制回路增益,KA,ωi和KR满足如下关系:

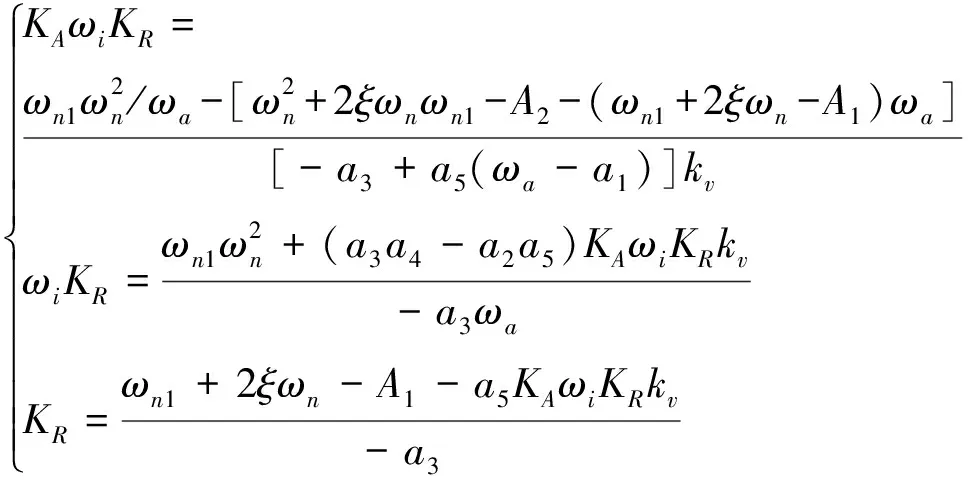
(13)

式中:ωa=a4-a2a5/a3=A4。

为方便后续描述,采用统一的表达形式描述系统开环传递函数为:

(14)

式中:

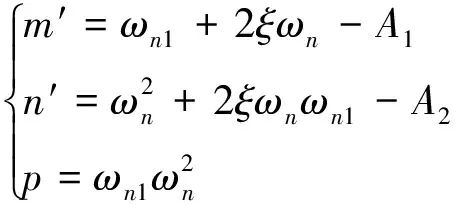
(15)

定义:

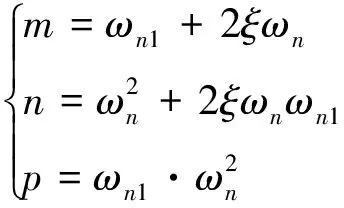
(16)

则:

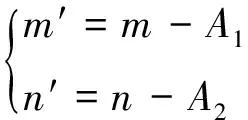
(17)

4 三回路过载驾驶仪参数设计

4.1 幅频-相频特性分析

根据系统开环传递函数HG(s),令s=jω,可得其幅频、相频特性:

(18)

定义复数:A(ω)和B(ω)如下:

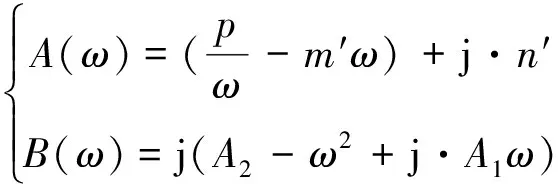
(19)

则复数A(ω)、B(ω)的幅值和相位分别为:

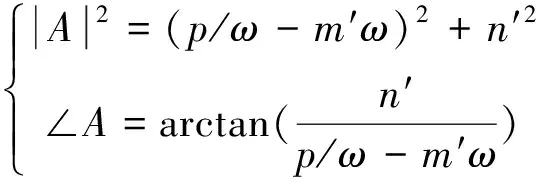
(20)

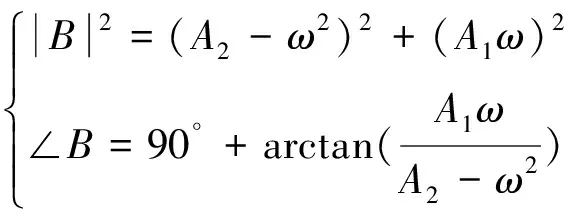
(21)

考虑惯性测量器件、舵机和结构滤波器等高频部件对系统特性的影响,定义等效执行机构模型:

GACT(ω)=Γ(ω)∠φ

(22)

式中:Γ(ω)和∠φ分别为等效执行机构幅频特性和相频特性。

则系统开环幅频-相频特性表示为:

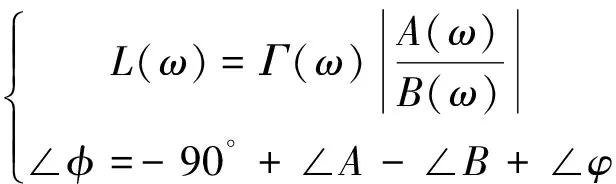
(23)

式中:L(ω)为系统开环幅频特性,∠φ为系统开环相频特性。

令系统开环幅值穿越频率为ω=ωCR,则有:

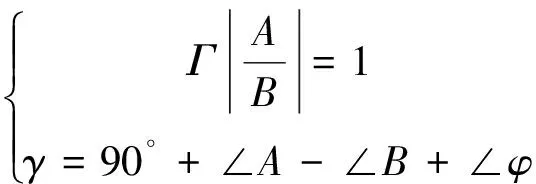
(24)

式中:γ为相位裕度。因此有如下关系式:

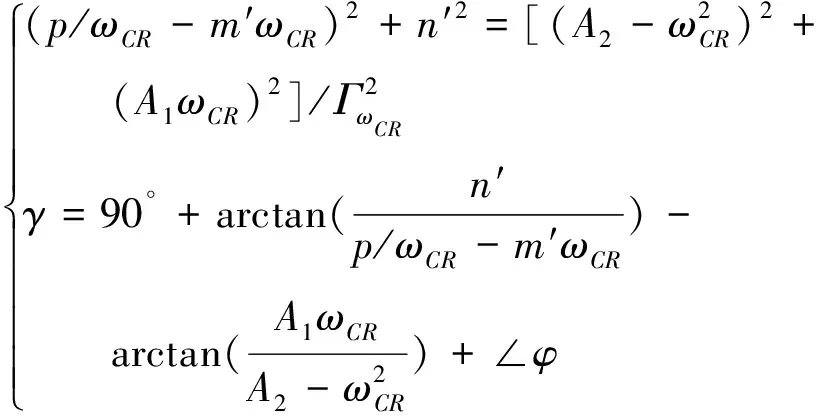
(25)

式中:ΓωCR为等效执行机构在幅值穿越频率ωCR处的幅值。

令系统开环相位穿越频率为ω=ωG,则有

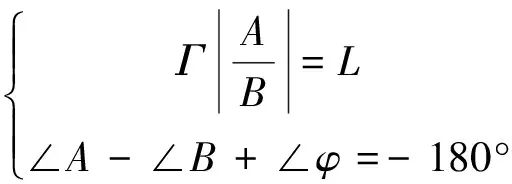
(26)

式中:L为幅值裕度。因此有如下关系式:

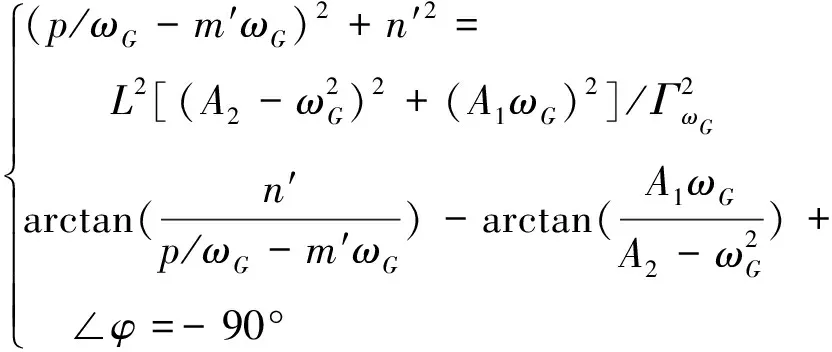
(27)

式中:ΓωG为等效执行机构在幅值穿越频率ωCR处的幅值。

4.2 开环截止频率的约束条件

定义:

对于式(27)有:

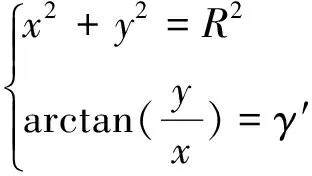
(28)

于是有:

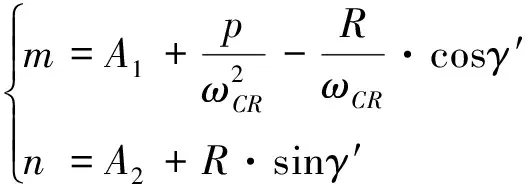
(29)

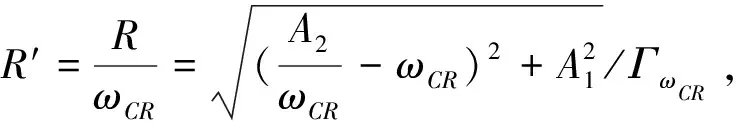
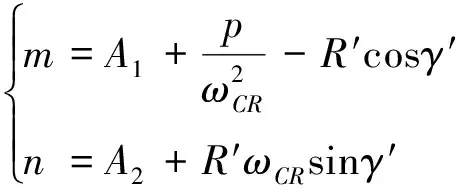
(30)

一般来说,工程设计中通常将ωCR作为系统带宽指标。系统开环截止频率的选择主要受系统舵机带宽、速率陀螺、加速度计及结构滤波器高阶动态环节性能的制约。为保证系统稳定性,且高频部件不对系统响应造成较大影响,工程上一般将自动驾驶仪开环截止频率ωCR取为高频部件等效带宽ωACT的1/3～1/5[6],保证高频部件在ωCR处引起的相移不超过30°。

4.3 最大舵偏角的约束条件

根据第3节分析可知,重新书写伪攻角反馈结构的闭环传递函数:

(31)

由此可得,从指令到舵偏角及舵偏角速度的传递函数:

(32)

(33)

根据文献[12-13],闭环系统响应的最大舵偏角速度在初始时刻产生,同时,注意到式(5),N0=-(a3a4-a2a5)KACKgkv,则有:

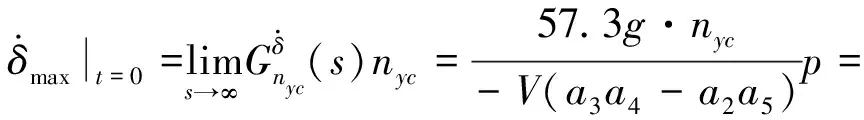
(34)

式中:δPH和αPH分别是指令为nyc时对应的平衡舵偏角和平衡攻角。

因此,考虑最大舵偏角速度约束,则有:

(35)

4.4 最小化闭环系统等效时间常数参数设计

根据式(16)和(30),可得如下关系:

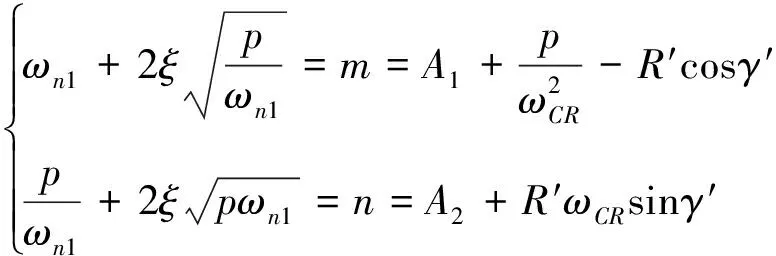
(36)

闭环系统等效时间常数为:

(37)

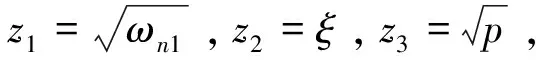
(38)

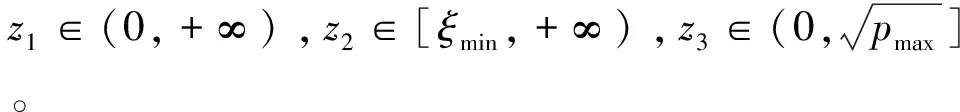
待优化目标函数为闭环系统等效时间常数:

(39)

综上所述,设计过程可以概述为:

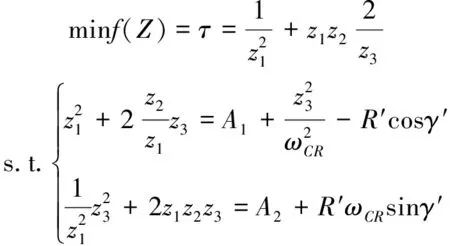
(40)

式中:

A1=a1+a4,A2=a2+a1a4,

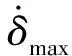
求解式(40)的最优解:Zopt=[z1·opt,z2·opt,z3·opt],则有:

(41)

当不指定相位裕度γ的设计值,而仅指定其范围γ∈[γmin,+∞)时,令z4=γ则设计过程表述为:

(42)

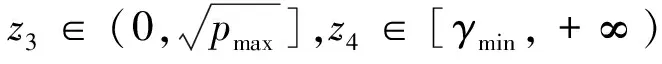
作此改进的目的是:当指定ωCR及γ,采用式(40)设计时,可能存在ωCR与γ不相容的情况。比如,对于静稳定导弹,若ωCR设定的不是很大,但γ设定的又比较小,在此情况下,则会导致式(40)无解。当ωCR与γ相容时,式(42)的最优解满足式(40)。即,使用式(42)按γ≥γmin寻优与使用式(40)指定γ=γmin寻优,结果一致;此时,对于式(42),按γ≥γmin寻优结果即是:γopt=γmin。

最后,使用系统幅值裕度对设计结果进行检验。

5 算例

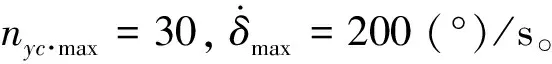
表1 弹体气动数据

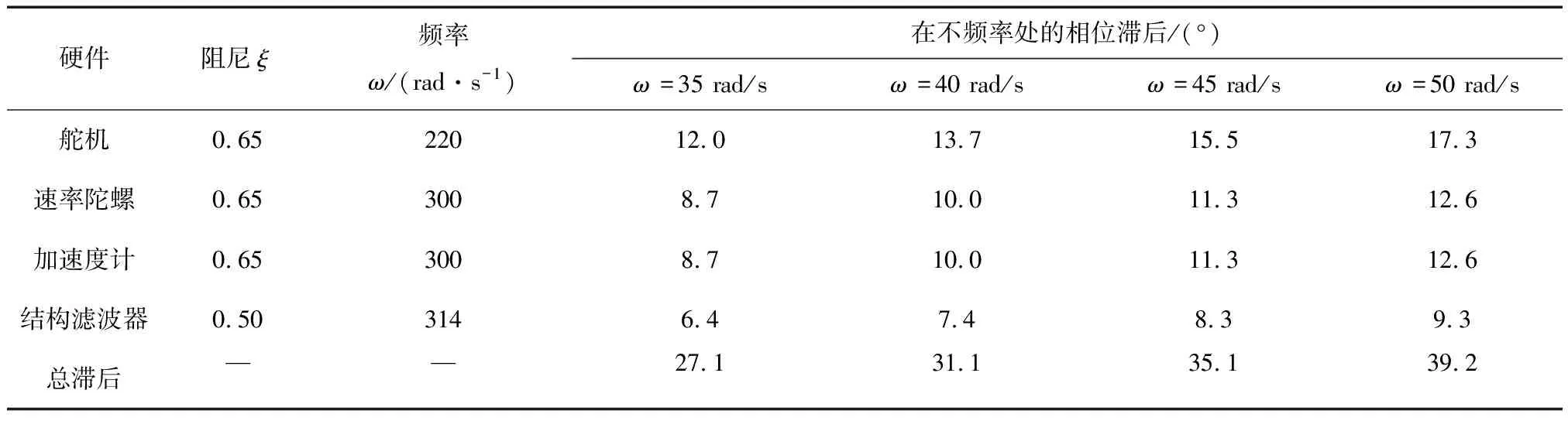
表2 硬件参数

对于上述硬件参数可以确定其等效执行机构的时间常数为[12]:

(43)

因此,可以取开环截止频率ωCR=(1/3～1/5)ωACT=18～30 rad/s。采用本文提出的方法,对上述数据描述的系统进行设计,取定截止频率ωCR分别为:40、45、50和55 (rad/s)及25、30、35和40 (rad/s);相位裕度γ=45°;阻尼比ξ≥0.6。对系统进行优化设计结果见表3所示。过载单位阶跃响应曲线、过载单位阶跃响应的舵偏角速度见图3～6所示。

表3 设计结果

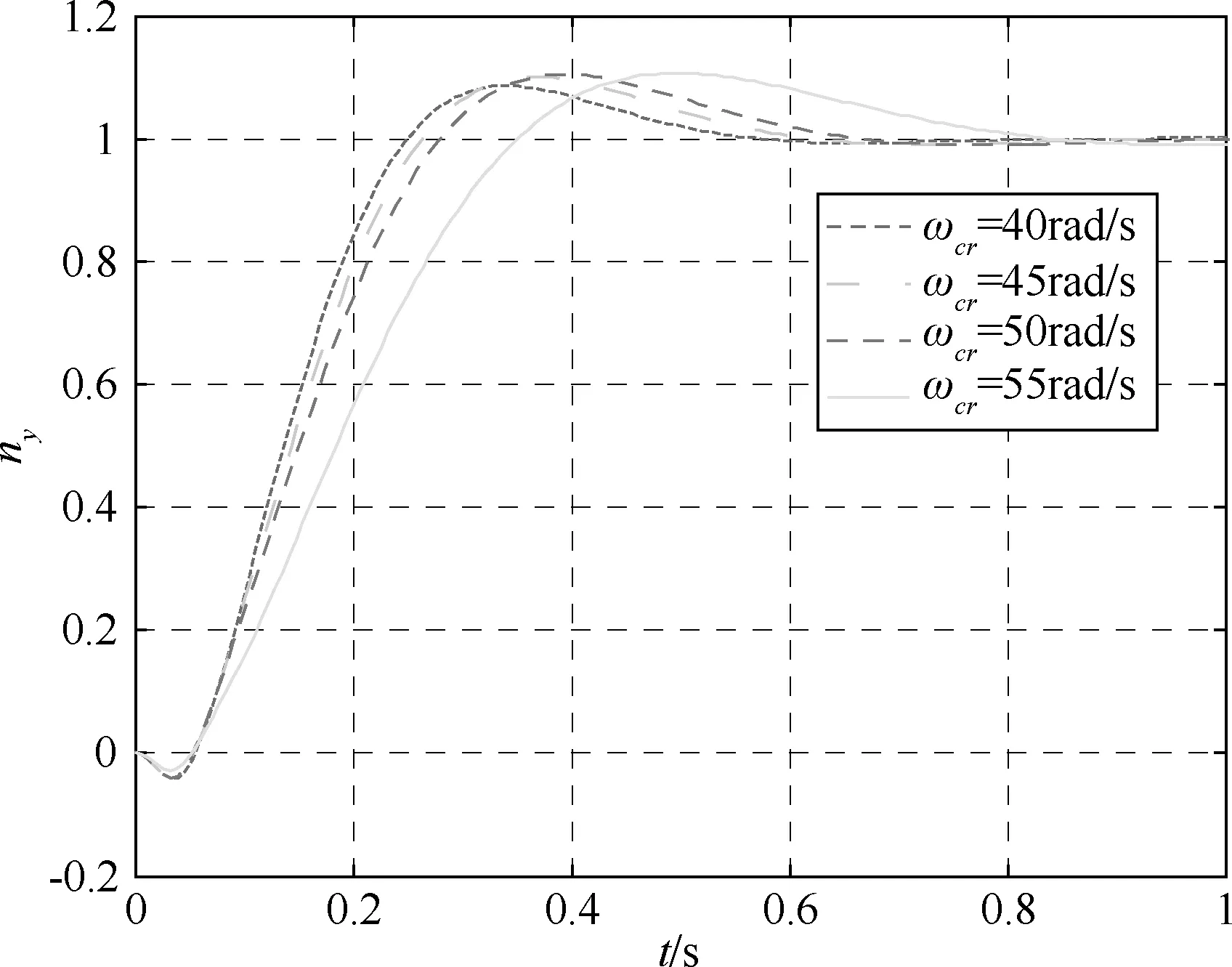
图3 过载单位阶跃响应(a2=250)

图5 过载单位阶跃响应(a2=-250)

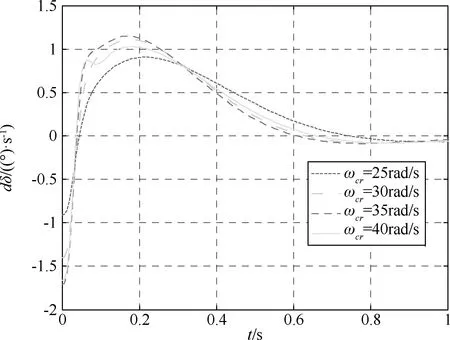
图6 过载单位阶跃响应下的舵偏角速度(a2=-250)

从表中序号1～3为“设置不匹配”的状态,按照γ≥γmin寻优,其余状态均按照指定的截止频率与相位裕度设计。序号5～7中,对于静不稳定状态,低频幅值裕度不满足大于6 dB要求,当截止频率提高到40 rad/s时,低频幅值裕度满足6 dB要求;但随着截止频率的提高,其高频幅值裕度逐渐减低,因此,对于静不稳定导弹,截止频率存在一个最优值,即在指定的相位裕度条件下,综合低频幅值裕度与高频幅值裕度。

6 结束语

通过对两种常用的三回路过载驾驶仪的分析,给出了统一的闭环传递函数和开环传递函数,由此得出当两种回路结构具有相同闭环极点时,两回路结构具有相同的开环传递函数,因此,证明了在数学意义上两种结构的等价性;同时,给出了两种结构下由闭环极点确定控制回路增益的表达式;其次,通过分析开环传递函数得到开环截止频率与相位裕度的关系式,并通过系统高频部件对开环截止频率进行约束,分析了闭环系统响应过程的最大角速度约束条件;最后,提出以最小化闭环系统时间常数为目标函数,通过求解带约束条件的系统最优解,实现系统开环截止频率、相位裕度的精确设计,并通过算例检验本文提出的设计方法的有效性。