大挠性航天器的模糊模型预测控制*

管 萍,黄明亮,戈新生,曹彧腾

北京信息科技大学自动化学院,北京 100192

0 引言

新一代航天器通常需要配备各种大型的挠性附件,与之前的常规航天器的挠性器件相比,大型挠性附件具有体积大、质量小、模态频率低且密集等特性,降低了负载指向精度,严重影响了航天器姿态控制的稳定性。故针对大型挠性航天器设计具有高精度、强鲁棒性和高稳定性的姿态控制策略是当前需要解决的难点问题之一[1]。

近年来,国内外学者们已将鲁棒控制、自抗扰控制以及容错控制等多种控制方法应用于挠性航天器中,获得了较好的控制效果[2-4]。然而,所研究的航天器均是挠性附件的质量和转动惯量在整星中占比较小的常规挠性航天器,中心刚体的运动受到挠性附件振动的影响较小。对于挠性附件的转动惯量和质量占整星的比重较大的大型挠性航天器高精度的三轴姿态控制,当前还鲜少有相关的研究。由于模型预测控制(model predictive control, MPC)的执行过程中引入了多步预测、滚动优化和反馈校正等多种控制策略,因此MPC有对模型的精确性要求不高和鲁棒性强的特性,为有效解决不确定性和扰动及各种约束的控制问题提出了良好的解决方法,目前MPC已经被广泛应用于化工、发电、航天等领域。近年来,已有学者将MPC算法应用在四旋翼飞行器、机器人轨迹跟踪等航空航天领域中,并取得了一些成果[5-7]。

相对于常规挠性航天器,大挠性航天器的挠性振动模态频率更低更密集,挠性附件的振动会引起系统未知的扰动,严重影响系统的姿态控制精度,甚至会破坏系统的稳定性。自适应模糊控制可以在整个控制过程中自适应地调整控制器的参数,从而逼近系统中的不确定量。文献[8]设计出一种基于模糊控制估计系统参数的自抗扰控制和模型预测控制的复合控制方法,可实现永磁同步电机的无速度传感器的运行。文献[9]提出了一种新型模糊控制算法,控制吸气式高超声速飞行器对高度和速度指令的稳定鲁棒跟踪。文献[10]设计了一种自适应模糊控制方法对具有不确定性摩擦的机械臂系统的控制效果良好。目前已有一些学者将自适应模糊控制应用于永磁同步电机、飞行器和机械臂等[8-10]。自适应模糊控制能很好地抑制系统中的不确定性扰动。

基于以上分析,本文将模糊模型预测控制应用于大挠性航天器的姿态控制中。先设置性能指标,求出性能指标最小时的模型预测控制律。随后,设计了相应的模糊控制器来逼近大挠性附件振动对姿态控制产生的未知扰动。对模糊规则参数的自适应律进行了推导,证明了姿态控制系统的稳定性,仿真结果验证了所设计控制方法可以实现对姿态角期望值的迅速跟踪,具有一定的鲁棒性。

1 大挠性航天器的数学模型

本文的研究对象为装有太阳帆板的大型挠性航天器,如图1所示,总体结构由安装在两侧的可转动的横向太阳帆板、中心刚体和旋转轴构成。

基于哈密顿原理和全局模态方法构建大型挠性航天器模型,假设航天器到达轨道预定位置并已完成了定向对日,锁定航天器本体与太阳帆板的相对偏转角,忽略轨道动力学影响的动力学模型为[11]:

(1)

(2)

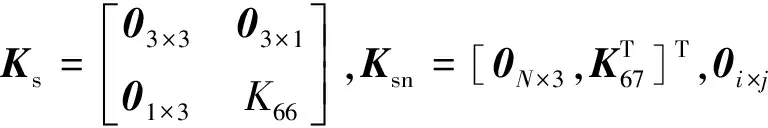
(3)

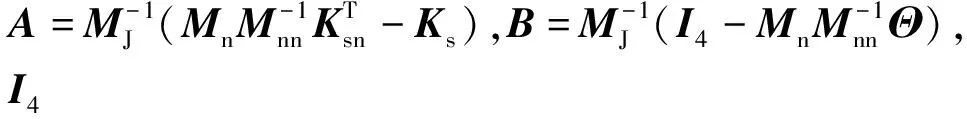
本文的控制目标为:在大挠性航天器系统(式(3))中,设计相应的模糊模型预测控制律,控制大型挠性附件振动快速衰减,使航天器的姿态角实现对期望值的迅速跟踪。

2 模糊模型预测控制

针对大挠性航天器的姿态控制,首先,通过泰勒公式对系统(式(3))设计相应的模型预测控制律。然后在此基础上,设计自适应模糊控制器逼近挠性振动产生的不确定扰动项D,以迅速衰减挠性振动,使航天器对姿态角指令迅速跟踪。

2.1 模型预测控制律的设计

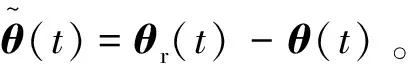
(4)

式中:可调时间参数T>0且控制参数λ>0。

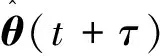
(5)

式中:

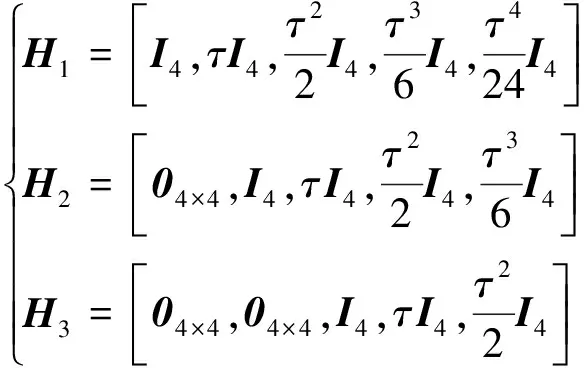
(6)

式中:

则性能指标(式(4))可近似写为:

(7)

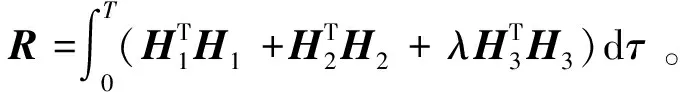
(8)

(9)

将式(9)代入到实际系统(式(3))中可得闭环系统方程:

(10)

根据K11和K12定义,可计算得

K11=42T2[25T8+4140T6+(218400λ+52416)T4+ 5019840λT2+25401600λ2]/K·I4

(11)

K12=52.5T[5T10+988T8+(56448λ+22032)T6+ (2028096λ+48384)T4+(13886208λ2+

4693248λ)T2+40642569λ2]/K·I4

(12)

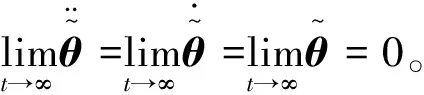
2.2 自适应模糊控制器的设计

在航天器运动过程中,安装在航天器上的大挠性附件会产生剧烈的振动,严重降低航天器姿态稳定性。在此将挠性附件振动对姿态的影响视作扰动,采用自适应模糊控制来逼近挠性振动引起的扰动D。

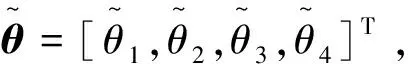
(13)

定义最优参数:

(14)

(15)

则由式(9)可得模糊模型预测控制律为:

(16)

将模糊预测控制律(式(16))代入实际系统(式(3))中,可得:

(17)

故误差方程为:

(18)

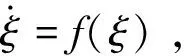
(19)

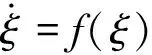
引理2[13]. 对实数变量z和实数变量ζ,任意大于0的常数μ,θ,ψ都存在:

(20)

定理1. 对于大挠性航天器姿态控制系统(式(3)),在模糊模型预测控制律(式(16))的作用下,模糊规则参数自适应律为:

(21)

式中:可调参数γi>0,则在有限时间内能使姿态误差e收敛至0。

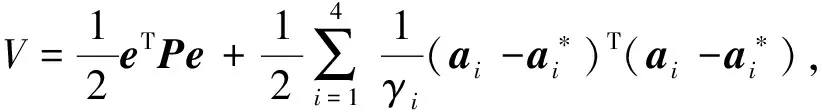
(22)

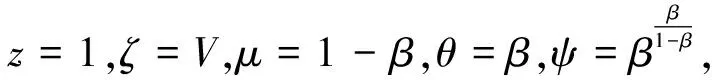
(23)

将式(23)代入式(22)中,可得:

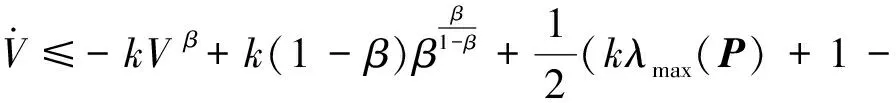
(24)

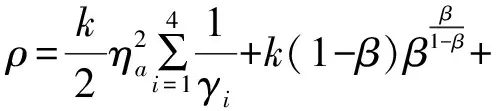
又因为k>0,0<β<1,由引理1可知,姿态误差e在有限时间内收敛到0,证毕。

基于以上分析,本文的主要控制思想是首先基于泰勒公式近似预测量,从而求解最优问题得到非线性预测控制律(式(9))。其次用模糊控制逼近系统(式(3))中的扰动项D,并推导出了相应的自适应律(式(21))。

3 仿真校验

将所设计的模糊MPC策略施加到大挠性航天器中,为了验证控制策略的有效性,进行了数字仿真和结果分析。大挠性航天器的参数如下:中心刚体的质量mR=120 kg,考虑航天器具有四阶模态的情况,即η=[η1,η2,η3,η4]T,中心刚体3个方向的转动惯量J=diag(20,20,20) kg·m2,太阳翼长度L=8 m,宽度b=1 m,厚度h=0.01 m,其余参数详见文献[11]。

为进行比较,将所设计的模糊MPC策略和传统MPC控制策略(文献[5])分别应用在大挠性航天器的姿态控制上。姿态控制的仿真结果如图2所示。在传统MPC控制策略的控制下,大型挠性航天器的姿态角和太阳能电池帆板转动角的响应时间分别为100 s、100 s、110 s和110 s,挠性模态η在200 s内还未趋于0。在模糊MPC控制策略的控制下,航天器三轴姿态角和太阳能帆板转动角的响应时间均在80 s内,挠性模态η在100 s后趋于0。

在实际工程中,在空间运行时,大型挠性航天器太阳帆板的收缩和伸展会引起挠性附件的转动惯量发生较大变化,从而导致航天器质量矩阵变化较大;同时航天器内部液体晃动、携带燃料的消耗等因素也会引起航天器的质量矩阵等参数发生变化,由此导致姿态控制系统的控制精度降低。故对质量矩阵Mx增加或减少20%的大挠性航天器姿态控制系统进行仿真验证,以检验所设计控制策略的鲁棒性。

当质量矩阵Mx增加20%时,姿态控制仿真结果如图3所示。在传统MPC策略的控制下,三轴姿态角和太阳能帆板转动角分别在120 s、120 s、130 s和130 s内达到期望值,在200 s内挠性模态η还未趋于0;在模糊MPC控制器的控制下,航天器三轴姿态角和太阳能帆板转动角均在80 s内跟踪上期望值,挠性模态η在100 s后趋于0。质量矩阵Mx减少20%时的仿真结果与增加20%时相似,限于篇幅,此处未将仿真结果列出。

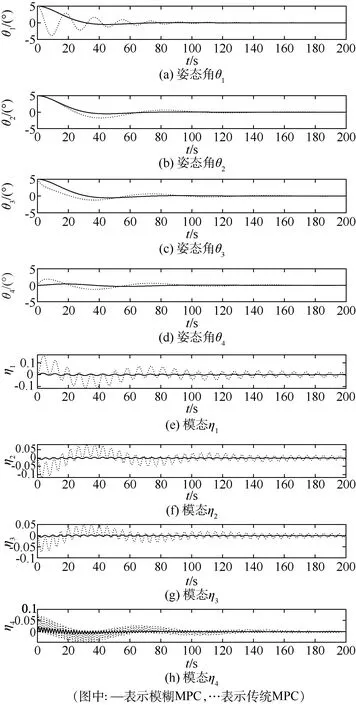
图3 Mx增加20%时,姿态角、挠性振动模态响应曲线

仿真结果表明,传统的MPC控制器能控制大挠性航天器的姿态角达到期望值,但其姿态角的响应时间较长,且挠性模态无法快速衰减趋于0。而本文设计的模型预测控制方法,通过泰勒公式求出了非线性预测控制律,进而有效地避免了由传统MPC在线求解优化问题造成的繁重计算量。而自适应模糊控制可迅速逼近由大挠性附件的振动引起的不确定干扰,故所设计的模糊MPC能快速衰减大挠性附件的振动,使姿态角响应速度更快。在质量矩阵参数发生变化时,所设计控制方法的姿态响应时间能基本保持不变。

4 结论

针对挠性航天器的大挠性附件振动严重影响航天器姿态控制精度的问题,设计了模糊模型预测控制策略。通过使用泰勒展开求解性能指标的最优问题,设计出相应的非线性模型预测控制律,从而减少了在线计算量。采用模糊控制逼近挠性振动引起的不确定扰动,使挠性振动快速衰减。仿真结果表明,所设计的模糊模型预测控制策略可有效地抑制大挠性附件的振动,实现航天器对期望姿态角度的迅速跟踪,具有较好的鲁棒性。