Lambert交会中转移时间的优化及应用

周楷程,余红英,樊永生

1. 中北大学电气与控制工程学院,太原 030051 2. 中北大学大数据学院,太原 030051

0 引言

在不考虑摄动的二体模型下,航天器的轨道转移问题可以归结为经典的Lambert 问题。对于固定速度增量条件下的Lambert问题,可根据给定速度增量求出转移时间,随即根据所求转移时间和参与轨道转移的两航天器位置矢量来确定转移轨道。针对此问题,学者们提出过多种不同的求解方案,经典的有Battin的a迭代法、Boltz的p迭代法和普适变量法[1-2],其中以普适变量法最为经典。经典普适变量法在两位置矢量共线,即转移角为0°或180°时会发生奇异,此时转移轨道是一条退化为直线的圆锥曲线,这在实际中是不可实现的[3]。

在航天工程中,通常需要选定一个或多个优化指标来确定轨道转移的优化问题。文献[4]研究与优化了Lambert变轨中最小能量轨道问题。文献[5] 研究与求解了能量最优Lambert问题。文献[6]研究与优化了双冲量交会问题的数值求解方法。文献[7]研究了共面椭圆轨道间转移所用最优燃料的Lambert问题。文献[8]研究了最优转移时间和最优燃料的Lambert问题,并采用混合遗传优化算法进行了求解。文献[9]对限制时间情况下,航天器轨道最优转移问题进行了研究,并采用粒子群算法进行求解。

本文在对相关文献深入研究的基础上,使用一种基于横向偏心率的Lambert交会求解算法,以求解横向偏心率为切入点,可避免出现奇异点的问题,并将转移时间表示为横向偏心率的函数;在固定速度增量条件下,选取转移时间作为轨道转移优化问题的优化指标是最合适的选择,利用自适应粒子群优化算法对轨道转移中转移时间进行优化,采用自适应惯性权重和自适应变异机制优化转移时间,达到用最短的转移时间在固定速度增量的情况下实现Lambert交会。

1 Lambert交会转移时间研究

针对经典普适变量法存在的奇异点问题,采用基于横向偏心率的Lambert交会求解算法以避免出现奇异点。从横向偏心率矢量出发,通过空间固定两点的圆锥曲线,其偏心率矢量在平行于两点弦长方向上的分量为常值,于是该轨道的偏心率可分解成垂直于弦长方向的分量和平行于弦长方向的分量。定义偏心率在垂直于弦长方向的分量为横向偏心率矢量。利用这一特性,可以证明通过空间固定两点的任意圆锥曲线可由横向偏心率矢量唯一确定。下面对算法原理进行推导[3,10-11],并将转移时间表示为横向偏心率的函数。

在轨道动力学中,轨道方程可由积分常数拉普拉斯积分推导和定义:

(1)

式中:H为比角动量,v为速度矢量,μ为引力常数,L为Laplace矢量,r为地心矩矢量,r为r的模。两边除以μ,并点乘r,得:

(2)

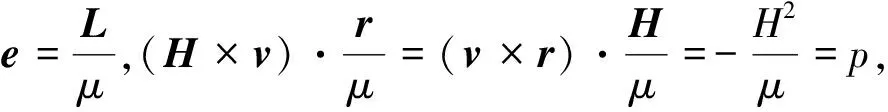
e·r=p-r

(3)

式中:e为偏心率矢量,p为轨道半通径。

基于横向偏心率矢量的Lambert问题的几何描述可以如图1所示。点Fe为地心引力中心,P1和P2两点分别是操控航天器转移的初始和目标位置,所对应的位置矢量为r1和r2,c为初始和最终位置之间的弦长,Δθ为位置矢量之间的夹角,e为飞行轨迹所对应的偏心率矢量。ωc为初始位置矢量r1与弦单位矢量ic之间的夹角。

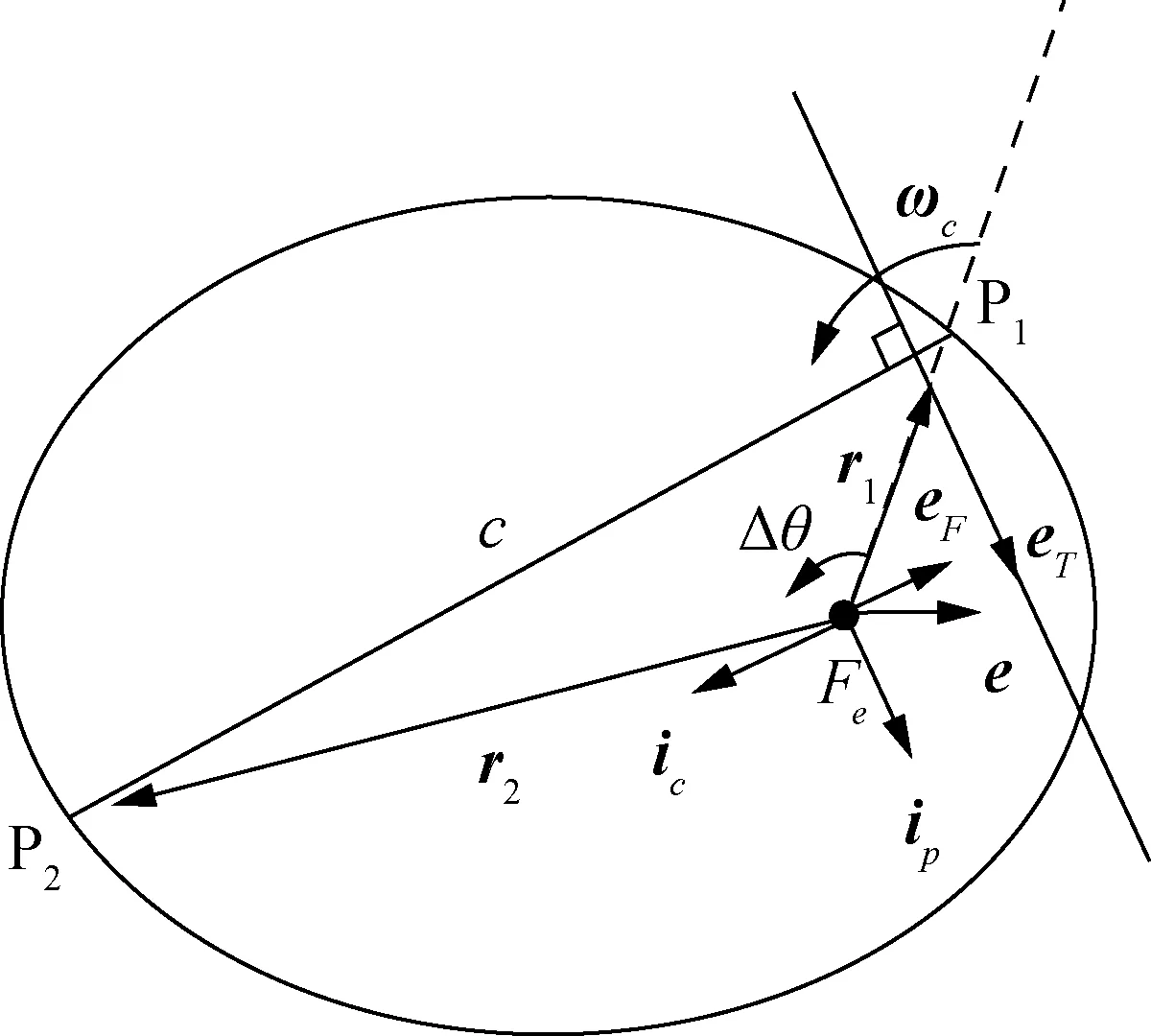
图1 基于横向偏心率矢量的Lambert几何描述

根据式(3),P1和P2两点对应地心矩矢量做差可得:

e·(r2-r1)=r1-r2

(4)

(5)

eF定义为切向偏心率矢量,式(5)中eF为切向偏心率矢量沿弦长方向的分量,ic定义为弦单位矢量。同时定义偏心率矢量沿垂直于弦长方向的分量为横向偏心率矢量,用eT表示。因此,经过P1和P2两点任意轨迹所对应的偏心率矢量可由沿弦长方向的分量eF以及垂直于弦长方向的分量eT共同表征:

e=eFic+eTip

(6)

ip是在轨道平面内垂直于弦长方向的单位矢量。由(6)式可以看出,经过P1、P2两点任意轨迹所对应的偏心率矢量在弦长方向的投影为常值,即eF=|r2-r1|/c。当eF→0时,轨迹偏心率矢量的极限方向就是垂直于弦长的方向;而当eT→0时,经过P1、P2两点轨道偏心率有极小值,即emin=eF。

定义偏心率极小值所对应的轨道为基础椭圆轨道,统一用下标F表示。于是,基础轨道的偏心率、半长轴和半通径分别为:

(7)

根据Battin经典Lambert算法中所推导的半通径表达式,有:

(8)

Δω为近地点相对于基础轨道偏心率矢量的转过角度,即tan(Δω)=eT/eF。函数σ(·)定义为:

(9)

由式(5)知σ(eF)=-σ(r2-r1),同时考虑到|eF|=σ(eF)eF,于是式(8)可表达成横向偏心率eT的函数,即:

(10)

轨道半长轴也可以表示为eT的函数:

(11)

在地心轨道坐标系中,ic和ip可以分别表示为:

(12)

根据偏心率矢量的几何定义,可以得到以下等式:

e=[ecosθ1,-esinθ1,0]T=
[eFcosωc-eTsinωc,eFcosωc+eTsinωc,0]T

(13)

P1点和P2点所对应的真近点角可以表示为:

(14)

式中:θ取值为[0,2π],arctan2(y,x)为反正切函数。根据偏近点角与真近点角之间的关系,所对应的偏近点角可以表示为:

(15)

由以上公式可知,给定变轨初始和最终的位置矢量r1和r2,转移轨道所对应的偏近点角E1和E2、半长轴a、以及偏心率e都可以表示为横向偏心率的函数。而给定偏近点角E1、E2、半长轴a、以及偏心率e,就可以求出从点P1转移到点P2所需要的转移时间t12,因此转移时间t12也是横向偏心率的函数,如下所示:

(16)

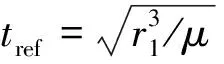
(17)

由以上推导可知,当取得航天器轨道六根数以及横向偏心率时可求出转移时间。并且当Δθ=0和Δθ=180°时不存在奇异,这一点优于经典普适变量法。

2 转移时间优化

在解决航天器的实际轨道交会问题时,常常是给定速度增量,求出转移时间,最终得到交会转移轨道。因此在充分利用速度增量的前提下如何得到最优转移时间就成了研究Lambert交会的一个重点。本文将采用自适应粒子群算法优化转移时间。

目前国内外常用于研究Lambert交会优化问题的算法有遗传算法和模拟退火算法等。这些算法基本上能寻找到优化路径,但算法涉及到粒子交叉等,过程较为复杂。而粒子群算法由于简单和易于实现,目前已广泛应用于航天器轨道转移优化等领域。

粒子群算法(Particle Swarm Optimization,PSO),PSO基于群体智能, 采用全局搜索策略寻优。粒子根据全局和自身最优位置更新速度[12]。

文献[9]对多脉冲共面转移问题进行了研究,并利用PSO优化共面转移轨道能量;文献[13]研究了四脉冲异面非圆轨道交会对接问题,并运用PSO进行了优化;文献[14]对限制时间情况下,航天器轨道最优转移问题进行了研究,并采用PSO进行求解。以上说明了PSO在航天器轨道转移优化方面的有效性。

2.1 粒子群算法基本流程

粒子群算法基本流程[15]: 1)目标搜寻空间为D维空间;2)粒子群由N个粒子组成; 3)第i个粒子目前运动速度为:vi=(vi1,vi2,…,viD); 4)第i个粒子在D维空间的位置为:Xi=(xi1,xi2,…,xiD);5)第i个粒子的历史最优位置为:Pi=(pi1,pi2,…,piD);6)粒子群历史最优位置为:Pg=(pg1,pg2,…,pgD);7)粒子按一定规律进行位置更新。

2.2 优化粒子群算法

经典粒子群算法存在一定的局限性,主要有以下2个问题:1)较难兼顾全局搜索和局部搜索,无法保证收敛速度;2)多样性低,当适应度方差为0时容易陷入局部最优的陷阱,算法出现提前收敛[16],无法得出最优转移时间。

针对以上问题,本文做了如下2点优化: 1)引入自适应惯性权重,针对不同的搜索问题可以调整全局和局部搜索的能力,提高算法性能;2)借鉴遗传算法的变异机制,引入自适应变异。

优化后的粒子群算法称为自适应粒子群算法(Adaptive Particle Swarm Optimization,APSO)。该算法在每次粒子更新后,判断粒子个体是否陷入局部最优陷阱,对于符合判断条件的粒子则对其进行变异操作,变异后的粒子能够跳出先前搜索到的局部最优位置,并在更大的空间中展开搜索,同时也保证了粒子群的多样性。

经过自适应优化后,本文用自适应粒子群算法求解最优转移时间的流程如:

图2 自适应粒子群算法求解最优转移时间流程图

2.3 优化粒子群算法具体实现

为了更好地得到转移轨道中的最优转移时间,2.2节中对粒子群算法进行了优化,本节将研究优化的具体实现。

1)引入自适应惯性权重,在算法开始搜索时希望惯性权重比较大,使算法跳出局部最优陷阱,以利于全局搜索;在搜索过程中希望惯性权重的值逐渐减小,以利于局部寻优,便于算法收敛,故使用式(18)计算惯性权重:

WI=(Wmax-Wmin)×(N-Nal)/N+Wmin

(18)

式中:WI代表自适应惯性权重,Wmax代表惯性权重的高值,Wmin代表惯性权重的低值,N代表种群的迭代数目,Nal代表已经迭代的次数,其中Wmax、Wmin和N为给定值,WI的值将随着Nal值的变化而变化。

2)引入自适应变异,当满足式(19)中的变异条件则进行变异:

σ<0.005与P:=(a+(b-a)×R/Rm)<0.3

(19)

式中:σ代表适应度方差,P代表变异率,Rm代表R所能返回的最大值,R代表随机函数,取值为(a,b)之间的随机数,本文取a=0,b=1。变异公式如式(20)和(21)所示:

Gi←Gi×Y

(20)

cos(2π×P))

(21)

式(20)和(21)中:G代表粒子每一维变量的最优位置,经过变异后原始值就会改变,本文变量为转移时间,i的取值范围为0～K,K代表变量的个数,a、b和P同式(19)。

3 仿真校验

1)测试说明

采用Visual Studio软件进行算法校验。给定操控和目标航天器的轨道六根数以及变轨总速度增量,进行4个算例的测试。

算例1:测试自适应粒子群算法的自适应惯性权重的变化,验证算法的有效性;

算例2:测试给定最优转移时间下输出的两次变轨的速度增量之和是否等于或近似等于给定的变轨总速度增量,验证算法的有效性;

算例3:测试自适应粒子群和经典粒子群算法输出的最优转移时间,验证算法的优越性;

算例4:测试两算法在不同迭代次数下运行1000次耗时情况,验证算法的优越性。

2)测试初始参数

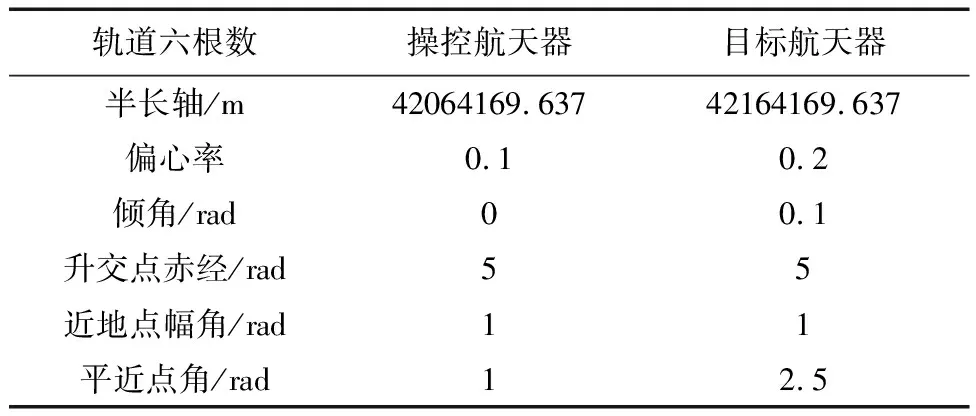
表1 操控和目标航天器的轨道六根数

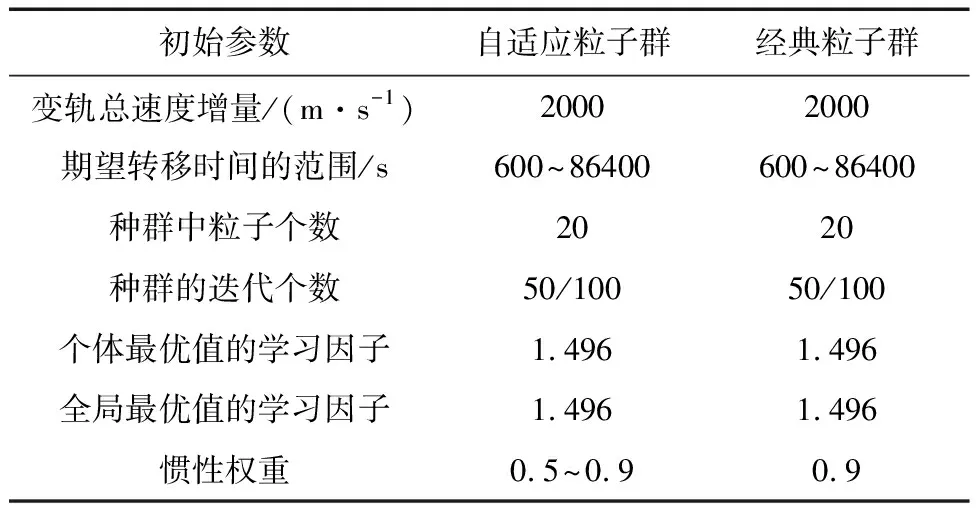
表2 自适应粒子群和经典粒子群算法初始参数

3)算例1

由于在算法初始化时已经迭代过一次,初始化时不需要惯性权重这一参数,因此惯性权重迭代次数测试为49次和99次。如图3所示,惯性权重值先大后小,与第2节理论相吻合,验证了自适应粒子群优化算法的有效性。

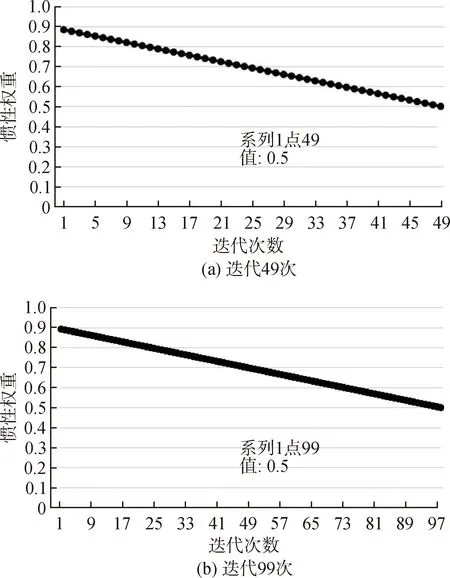
图3 自适应粒子群算法惯性权重随迭代次数的变化图

4)算例2

经多次迭代测试自适应粒子群算法,得到转移时间稳定在37750 s,因此以37750 s作为给定转移时间,测试变轨速度增量。

操控航天器为了完成轨道交会,会进行2次变轨,历次变轨时刻(相对于初始时刻的偏移量)和变轨速度增量如表3所示:

表3 变轨速度增量

根据表3所示,验证变轨速度增量。记总速度增量为v:

(22)

第一次变轨x,y和z分量记为x1,y1和z1;第二次变轨x,y和z分量记为x2,y2和z2,代入式(22),验证结果为v=2000 (m/s)。

经验证,实际总速度增量与给定变轨速度增量相吻合,证明了Lambert交会求解和自适应粒子群算法的有效性。

5)算例3

图4(a)中带折线散点的经典粒子群2和单折线的自适应粒子群得到的最优转移时间基本一致,无折线散点的经典粒子群1因为陷入了局部最优的陷阱,无法得到最优转移时间;图4(b)中2种算法得到的最优转移时间基本一致。

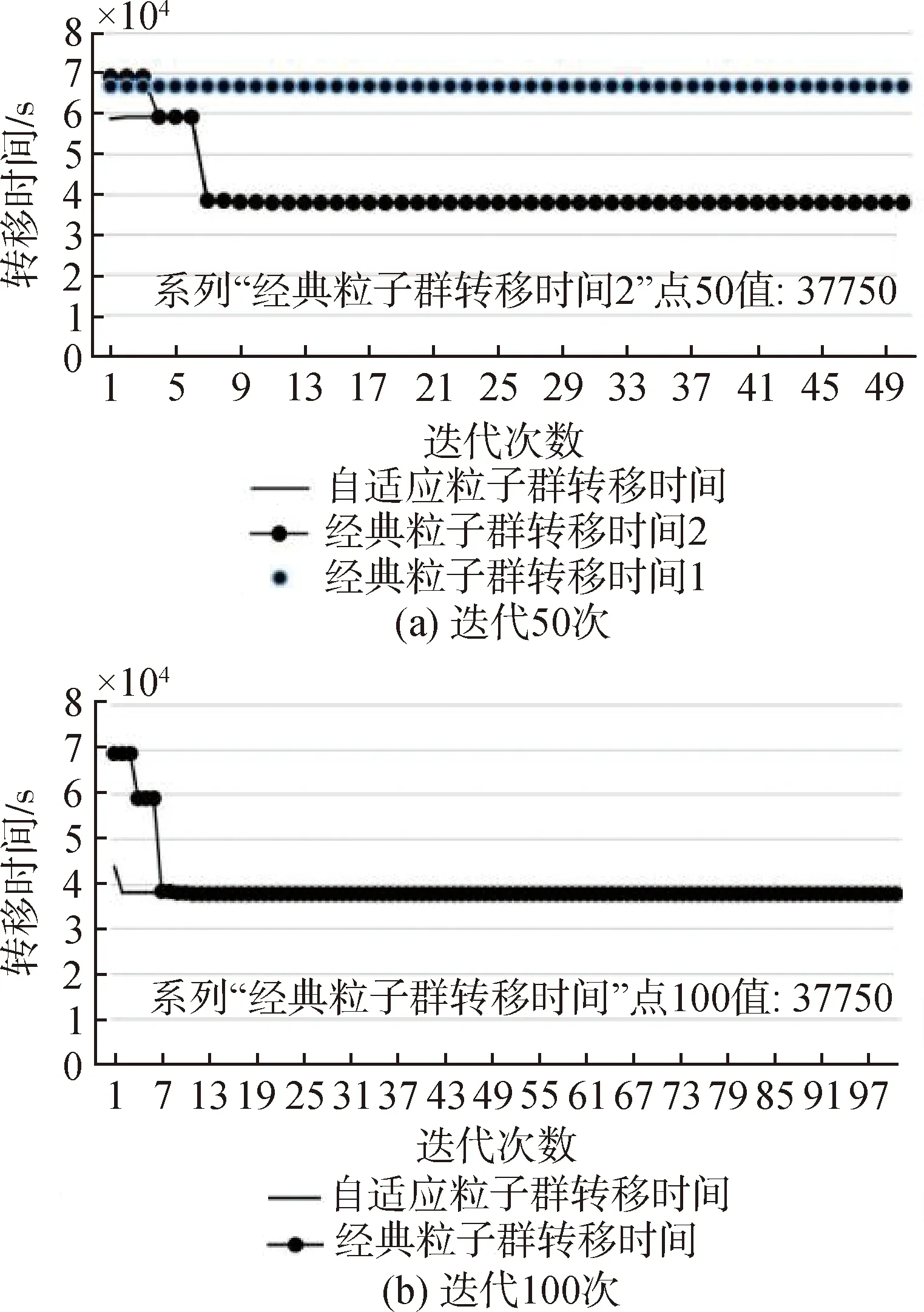
图4 迭代50次和100次自适应粒子群和经典粒子群输出转移时间对比

6)算例4

表4表示2种算法在迭代50次、100次和200次下重复运行1000次所花费的时间。由表4结果可知,本文所用自适应粒子群算法效率比经典粒子群算法高7%以上,并且随着迭代次数的增加,效率提升越明显。

表4 自适应粒子群与经典粒子群算法运行时间对比

4 结论

针对固定速度增量条件下Lambert交会中的转移时间,主要做了如下工作:

1)使用基于横向偏心率的Lambert交会求解算法研究转移时间,该算法与经典普适变量法相比,优势是不存在奇异点,解决了经典普适变量法存在的奇异点问题,并将转移时间表示为横向偏心率的函数;

2)在给定速度增量的条件下,采用自适应粒子群优化算法得出最优转移时间。该算法针对经典粒子群算法存在的问题,引入自适应惯性权重和自适应变异机制进行优化;

3)测试了自适应惯性权重的变化和变轨速度增量,证明了本文所研究算法的有效性;对自适应粒子群算法和经典粒子群算法进行对比测试,测试结果表明本文所用自适应粒子群优化算法能跳过局部最优陷阱,并且求解效率比经典粒子群算法高至少7%;经以上测试表明本文研究算法可应用于航天器空间交会。