一种补偿t-OPT噪声的冗余捷联惯组故障检测方法*

王永刚,毛博年,高 东

1. 中国科学院国家空间科学中心复杂航天系统综合电子与信息技术重点实验室,北京 100190 2. 中国科学院大学计算机科学与技术学院,北京 100049

0 引言

在对系统的可靠性和安全性有极高要求的航空航天领域,如果捷联惯组出现故障,可能会直接导致任务的失败,所以捷联惯组的可靠性对于提高载体的生存能力具有重要意义。与提高惯性传感器的元器件质量和制造工艺等方式相比,冗余设计通过增加器件的数量大幅提升了系统的可靠性[1],同时为故障检测方法提供了硬件基础。

目前对于冗余捷联惯组的故障检测,常采用基于等价空间原理的故障检测方法[2],等价空间法对冗余测量信息解耦,得到与系统状态无关的奇偶残差,通过检测残差量的变化判断系统故障信息,可以得到很好的检测效果。许多文献对等价空间法进行了相关的研究和扩展,文献[3-5]解决了等价空间法对于四轴冗余惯性传感器无法实现故障隔离的问题;文献[6-7]提出了检测冗余捷联惯组多故障的方法;文献[8-9]中解耦矩阵的构造方式可以检测出系统冗余捷联惯组特定轴的故障。

根据具体实现方式的不同,可将等价空间法分为广义似然比法[10]、最优奇偶向量法(Optimal Parity Vector Technology,OPT)[11-12]和奇异值分解法[13],其中,OPT方法提高了系统解耦的鲁棒性,但在构造故障检测函数时,未考虑奇偶残差统计特性的未知性,降低了故障检测方法的适用性。

冗余捷联惯组载体在机动时,惯性传感器的刻度系数误差、安装误差等误差项会使奇偶残差偏大,导致故障检测函数在系统未发生故障时就超过故障阈值,因此需要提前采取措施将测量误差标定[14]或者使用卡尔曼滤波[15-16]等方法将误差项补偿掉。文献[17]针对滤波方法会抑制奇偶残差中故障项的问题,提出使用交互式多模型方法补偿奇偶残差,但这些补偿方法均没有补偿随机噪声,导致检测方法的虚警率较高,而且无法有效检测低故障幅值的常值漂移故障。

本文依据基于等价空间原理的OPT方法,提出了一种补偿故障检测函数噪声的t检验最优奇偶向量法(t-OPT),该方法的特点在于:使用奇偶残差样本的统计量构造了新的故障检测函数,使用卡尔曼滤波算法补偿了故障检测函数中的随机噪声,降低了随机噪声对故障判决的干扰,提高了故障检测方法在冗余捷联惯组故障检测中的适用性和鲁棒性,最后通过仿真实验证实了该方法的有效性。

1 等价空间原理

等价空间法的基本原理是根据冗余捷联惯组的测量方程构造解耦矩阵,利用解耦矩阵将系统状态与系统故障分离,然后根据解耦后的等价方程进行系统的故障检测。

1.1 冗余捷联惯组测量模型

捷联惯组的冗余方式包括系统级冗余(如3套捷联惯组同轴共基座安装)和器件级冗余(如5个陀螺沿圆锥面均匀分布安装,6个陀螺沿正十二面体的6个法向安装),以三套捷联惯组同轴共基座安装方式为例,冗余捷联惯组的传感器安装矩阵H为[9]:

(1)

假设冗余捷联惯组有n(n>3)个陀螺或者加速度计,传感器测量误差只包含随机噪声,可得冗余捷联惯组的测量方程为[4]:

Z=HX+bf+ε

(2)

式中:Z∈Rn为n个惯性传感器的输出值,n为惯性传感器的个数,H∈Rn×3为冗余捷联惯组的传感器安装矩阵,X∈R3为三维状态信息(加速度或者角速度信息),bf∈Rn为故障向量,其对应于有故障惯性传感器的元不为0,其他元均为0,ε∈Rn是均值为0,方差为σ2In的随机噪声。

1.2 系统解耦

定义矩阵V∈R(n-3)×n为式(2)所示测量方程的解耦矩阵,解耦矩阵的约束条件为:

(3)

式中:H∈Rn×3为冗余捷联惯组的传感器安装矩阵,n为惯性传感器的个数。

对于解耦矩阵V的构造,文献[9]提出以传感器安装矩阵H的正交投影阵W=I-H(HTH)-1HT为基础,选取正交投影阵行向量组中的一个极大无关组,并进行施密特正交化,从而得到冗余测量方程的解耦矩阵V。

利用解耦矩阵V,根据式(2)可得到如下所示的等价方程:

P=VZ=Vbf+Vε

(4)

式中:P∈Rn-3称为等价向量。

由式(4)可见,等价向量仅与随机噪声和可能出现的故障相关,如果惯性传感器发生故障,等价向量的均值会发生变化,由等价向量在无故障和有故障情况下的不一致性,为故障检测提供了参考。但仅根据等价向量无法实现对故障器件的定位,需要采取措施对等价空间法进行具体的实现,所以本文在OPT方法的基础上提出了t-OPT方法。

2 t-OPT方法

等价空间法中的解耦矩阵V由冗余捷联惯组的传感器安装矩阵H确定,为了降低传感器安装矩阵编排方式对故障检测性能的影响,OPT方法构造了对特定惯性传感器敏感的最优奇偶向量(又称最优解耦向量),提高了系统解耦的鲁棒性[11]。但OPT方法在构造故障检测函数时引入了未知参数,为提高OPT方法在冗余捷联惯组故障检测中的适用性,本文提出了t-OPT方法,该方法在OPT方法的基础上构造了新的故障检测函数。

2.1 OPT方法

OPT方法针对冗余系统中的每个惯性传感器,定义了与各个惯性传感器对应的最优解耦向量vi,考虑解耦约束条件viTH=0,最优解耦向量可以表示为式(3)中解耦矩阵V各行的线性组合,然后通过最大化性能指标函数Si,使得最优解耦向量vi对第i个惯性传感器敏感,而对其他惯性传感器和随机噪声不敏感,最优解耦向量的约束条件可总结为[12]:

(5)

式中:vi∈Rn为第i个惯性传感器的最优解耦向量,n为惯性传感器的个数,H∈Rn×3为冗余捷联惯组的传感器安装矩阵,V∈R(n-3)×n为解耦矩阵,ci为解耦矩阵V线性组合的坐标向量,ei为n阶单位矩阵In的第i个列向量,viTei和viTej分别表示第i个惯性传感器的最优解耦向量对第i个和第j个惯性传感器故障的敏感度,‖viT‖表示对随机噪声的敏感度。

根据式(5)所示的约束条件可求得各个惯性传感器的最优解耦向量:

vi=VT(V(2In-eieiT)VT)-1Vei

(6)

利用最优解耦向量vi,根据式(2)可得到各个惯性传感器的奇偶残差:

ri=viTZ=viTbf+viTε

(7)

式中:ri为第i个惯性传感器的奇偶残差,bf∈Rn为故障向量,ε∈Rn是均值为0,方差为σ2In的随机噪声。

OPT方法为构造故障检测函数,以正态检验法为基础,假设惯性传感器无故障,由式(7)可得奇偶残差ri～N(0,σ2‖viT‖2),对奇偶残差进行标准化处理,得到各个惯性传感器的故障检测函数:

(8)

对给定的显著性水平α,由标准正态分布的分位点得到OPT方法的故障阈值:

Td=z1-α

(9)

根据式(8)～(9)和正态检验法,OPT方法的故障判决策略为:比较n个惯性传感器的故障检测函数,如果Dm为Di中的最大值,当Dm>Td时,则判定第m个惯性传感器发生故障,否则认为所有惯性传感器均无故障。

2.2 OPT方法的改进

由式(8)可见,OPT方法的故障检测函数中含有参数σ,在实际情况中,随机噪声的标准差σ是未知的,所以OPT方法不能依据正态检验法构造故障检测函数。为了提高OPT方法的适用性,本文提出了t-OPT方法,该方法依据t检验使用奇偶残差样本的统计量构造了新的故障检测函数,同时为提高样本的代表性,增加了奇偶残差的样本容量。

根据式(7)中奇偶残差在无故障和有故障情况下统计特性的差异,针对第i(i=1,2,…,n)个惯性传感器,提出如下无故障假设H0与有故障假设H1:

H0:ri～N(0,σ2‖viT‖2)

(10)

H1:ri～N(viTbf,σ2‖viT‖2)

(11)

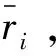
(12)

(13)

由式(12)和(13)可见,样本均值和样本方差的概率密度函数中均含有未知参数σ,为消除未知参数,根据t分布的定义[18],使用样本均值和样本方差构造如下统计量:

(14)

化简后得到服从t分布的检验统计量:

(15)

根据式(15),构造各个惯性传感器的故障检测函数:

(16)

对给定的显著性水平α,根据t分布的分位点得到t-OPT方法的故障阈值:

Td*=t1-α(l-1)

(17)

式中:l为样本个数。

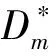
由式(16)可见,故障检测函数中的所有参数均可由奇偶残差样本的统计量求得,所以t-OPT方法相较于OPT方法具有较好的适用性。

3 故障检测函数噪声的补偿

由式(7)可见,各个惯性传感器的奇偶残差仅与传感器的故障和噪声相关,通过降低噪声的方差,可以使检测方法具有较低的虚警率和较好的小故障检测能力。所以为进一步提高t-OPT方法的适用性和鲁棒性,本文采用卡尔曼滤波算法补偿了t-OPT方法中故障检测函数的随机噪声。

以冗余捷联惯组中的一个惯性传感器为例,由式(16)得到该惯性传感器的故障检测函数g:

(18)

将故障检测函数建模为随机常数f作为离散状态方程,将式(18)所示的方程作为离散测量方程,并且定义测量方程中的噪声为ε′,得到惯性传感器故障检测函数计算模型:

fk=fk-1+βk-1

(19)

(20)

(21)

Jk/k-1=Jk-1+Qk-1

(22)

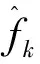
Kk=Jk/k-1/(Jk/k-1+Rk)

(23)

(24)

Jk=(1-Kk)Jk/k-1

(25)

因此,补偿故障检测函数的噪声后,t-OPT方法的故障检测流程可总结为:

1)根据式(3)计算冗余捷联惯组测量方程的解耦矩阵V;

2)根据式(6)计算每个惯性传感器的最优解耦向量vi;

3)根据式(7),由最优解耦向量vi得到各个惯性传感器的奇偶残差;

5)对于给定的显著性水平α,根据式(17)得到故障阈值Td*;

4 仿真校验

为了验证方法的有效性,建立仿真平台,设定故障检测仿真条件如下:

1)三套捷联惯组为同轴共基座冗余配置方式,陀螺序号与式(1)中传感器安装矩阵的行号一致;

2)冗余捷联惯组中陀螺的噪声标准差σ=0.1(°)/h;

3)设定显著性水平α=0.95,选取样本个数l=16,则OPT方法的故障阈值为Td=z1-0.95=1.645,t-OPT方法的故障阈值为Td*=t1-0.95(16-1)=1.7531;

4)在惯性传感器的刻度系数误差、安装误差等误差项已被标定或补偿的条件下,设定载体运动场景1为载体匀速直线运动,运动场景2为载体机动运行(三轴角运动设为X:50sin(8πt)(°)/s,Y:50cos(πt)(°)/s,Z:50t(°)/s),分别在两种运动场景下选取冗余捷联惯组载体运动时长为10 s的陀螺输出数据作为方法性能验证数据,采样频率为100 Hz;

5)故障建模:常值漂移和线性漂移是惯性传感器常见且不易察觉的故障,在仿真中,将常值漂移建模为幅值可调的阶跃函数,将线性漂移建模为斜率可调的斜坡函数;

6)虚警率:冗余系统无故障时,所有陀螺故障检测函数中的最大值超过故障阈值的概率;漏检率:冗余系统有故障时,故障陀螺的故障检测函数不是最大值或者是最大值但低于故障阈值的概率。

4.1 常值漂移故障检测仿真

当载体分别处于运动场景1和2时,以设定的仿真条件为基础,在第4秒对冗余捷联惯组的陀螺1注入故障幅值为5σ的常值漂移故障,使用补偿噪声后的t-OPT方法对冗余捷联惯组进行故障检测,得到两种运动场景下所有陀螺的常值漂移故障检测曲线如图1～2所示。

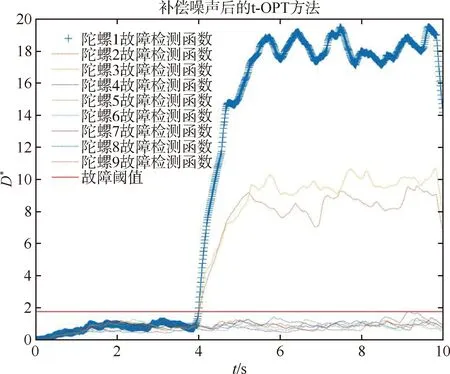
图1 运动场景1下所有陀螺的常值漂移故障检测曲线

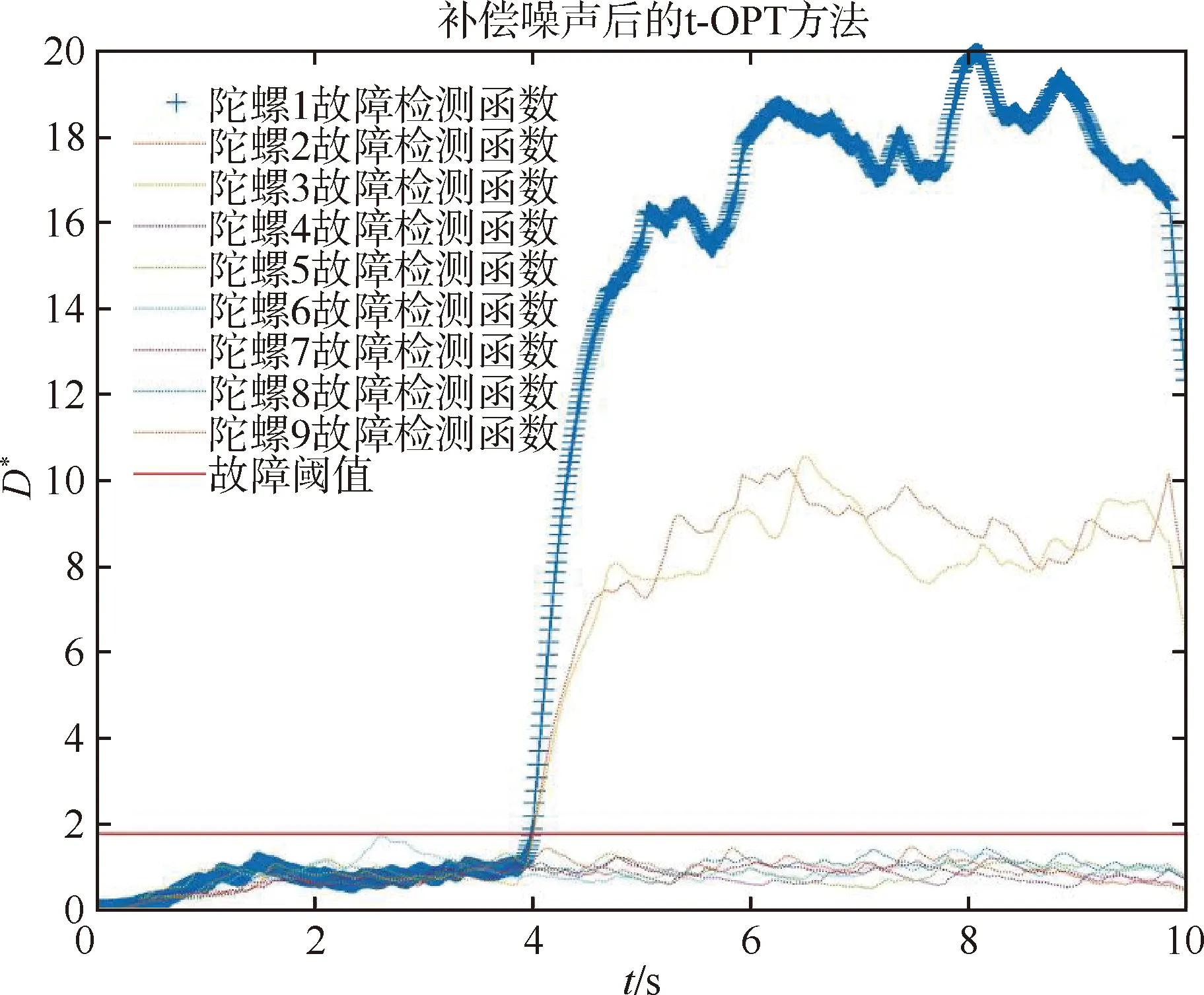
图2 运动场景2下所有陀螺的常值漂移故障检测曲线

为比较不同故障检测方法的故障检测能力,当载体处于运动场景1时,在第4秒对冗余捷联惯组的陀螺1注入故障幅值为5σ的常值漂移故障,分别使用OPT方法、t-OPT方法和补偿噪声后的t-OPT方法对陀螺1进行故障检测,得到陀螺1的常值漂移故障检测曲线如图3所示。

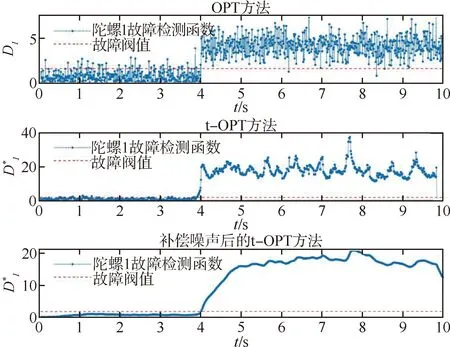
图3 运动场景1下陀螺1的常值漂移故障检测曲线

为分析对比故障检测方法的小故障检测能力,当载体处于运动场景1时,在第4秒对陀螺1注入不同故障幅值的常值漂移故障,进行1000次随机实验并记录仿真结果的虚警率和漏检率,实验结果如表1和2所示。

表1 运动场景1下常值漂移故障检测虚警率

表2 运动场景1下常值漂移故障检测漏检率

分析常值漂移故障检测仿真结果:

1)如图1～2所示,注入故障后,所有陀螺的故障检测函数中,陀螺1的故障检测函数值最大且超出故障阈值,与t-OPT方法的故障判决策略一致,而且故障检测结果与载体运动场景无关。

2)如图3所示,注入故障后,3种方法的故障检测函数在第4秒后均明显变大且超出故障阈值。但OPT方法使用了仿真条件中的噪声标准差σ,在实际情况中噪声标准差是未知的。而t-OPT方法使用奇偶残差样本的统计量就可以判断出故障陀螺,提高了方法的适用性。

3)如表1所示,OPT方法和t-OPT方法的故障检测虚警率均较高,导致陀螺在无故障时经常被判定为出现故障。使用卡尔曼滤波算法补偿t-OPT方法中故障检测函数的噪声后,故障检测虚警率降至0.55%,进一步提高了方法的适用性。

4)如表2所示,当故障幅值低于7σ时,OPT方法的故障检测漏检率较高,而t-OPT方法的故障检测漏检率较低,补偿噪声后,t-OPT方法的漏检率得到了进一步的降低。

5)结合表1和2,当陀螺故障幅值较低时,通过补偿t-OPT方法中故障检测函数的噪声,可以明显降低故障检测的虚警率和漏检率,使检测方法可以有效检测到低故障幅值的常值漂移故障,说明补偿噪声可以提高t-OPT方法的鲁棒性。

4.2 线性漂移故障检测仿真

当载体处于运动场景1时,在第4秒对陀螺1注入斜率为0.001的线性漂移故障,分别使用OPT方法、t-OPT方法和补偿噪声后的t-OPT方法对冗余捷联惯组进行故障检测,得到陀螺1的线性漂移故障检测曲线如图4所示。

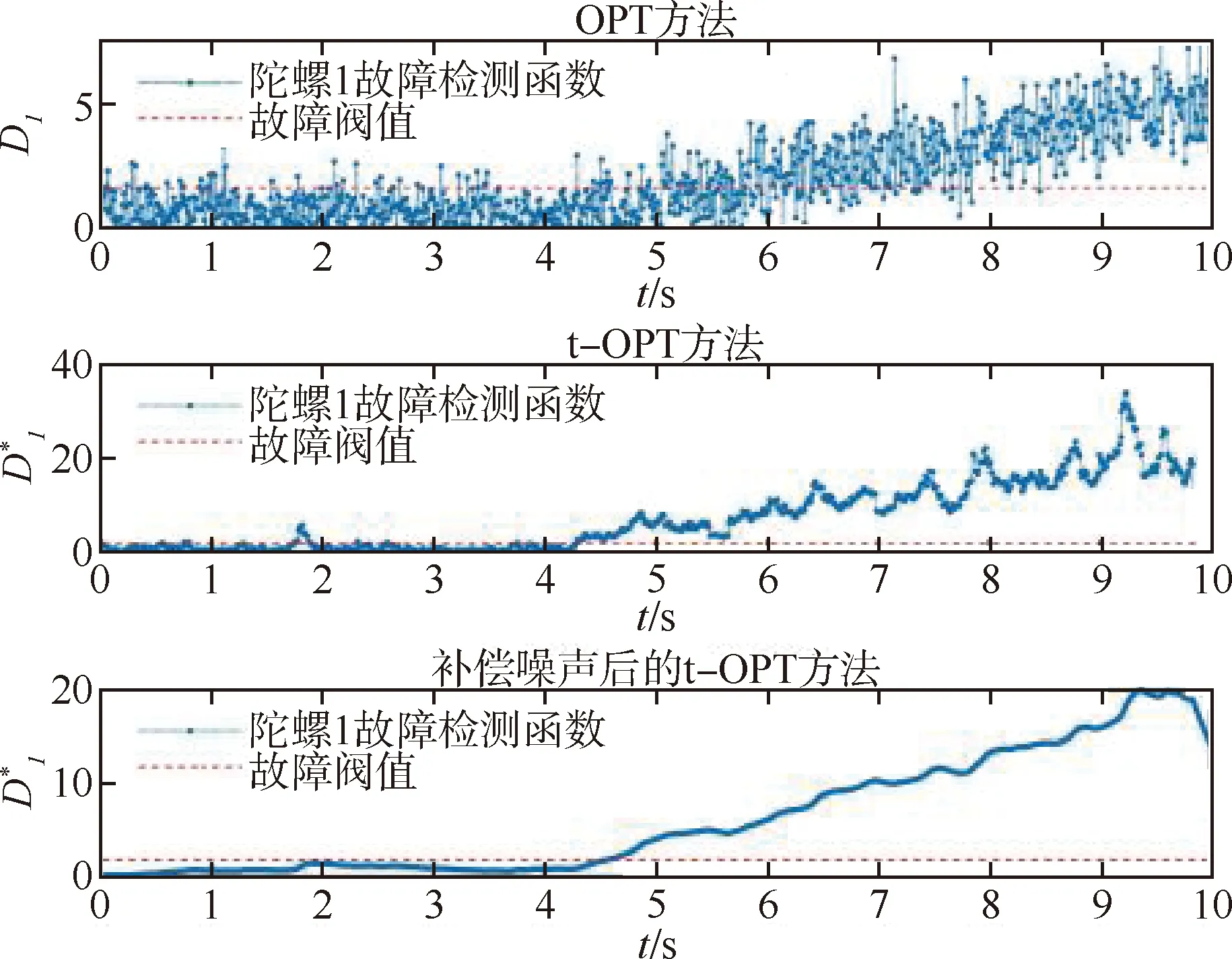
图4 运动场景1下陀螺1的线性漂移故障检测曲线

如图4的线性漂移故障检测曲线所示, OPT方法的故障检测时延约为4 s,而t-OPT方法的故障检测时延仅为0.2 s左右,但虚警现象仍较严重,通过补偿t-OPT方法中故障检测函数的噪声,有效降低了故障检测的虚警率。

由于线性漂移故障的渐变特性,陀螺出现故障初期,故障幅值极低,所以线性漂移的故障检测有一定的延时性。由表1～2可知,补偿噪声后的t-OPT方法可以有效检测到低故障幅值的常值漂移故障,所以在线性漂移故障检测中表现为故障检测时延较低。

5 结论

对于冗余捷联惯组的故障检测,在OPT方法的基础上,提出了一种补偿故障检测函数噪声的t-OPT方法。该方法使用奇偶残差样本的统计量构造了新的故障检测函数,补偿了t-OPT方法中故障检测函数的随机噪声,提高了故障检测方法的适用性和鲁棒性。仿真结果表明,该方法相较于OPT方法具有较低的虚警率,可以准确检测到低故障幅值的常值漂移,有效降低了线性漂移故障的检测时延。