以终为始：结果导向型思维在数学教学中的应用研究

陈莹

［摘 要］结果导向型思维方式是从最终的结果出发，反向分析过程或原因，寻找关键信息，找到解决问题的方法。在小学数学教学中培养学生的结果导向型思维，以终为始，有利于学生打破思维定式，提升解决问题的效率。结果导向型思维可以运用于运算、解决问题、几何图形等领域，改变学生的固有思维，拓宽学生的思维广度。

［关键词］结果导向型思维；解决问题；数学游戏

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）11-0074-04

一、现状分析

自2013年起，笔者所在的数学团队就开始实践数学游戏教学。在多年的一线教学中笔者发现，大部分学生在解决数学游戏问题的过程中会选择最容易想到的方式，而非最便捷的方式。

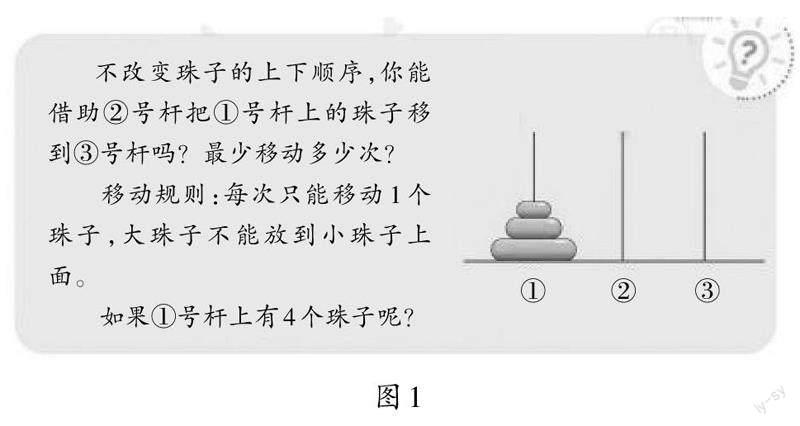
比如，解决人教版教材四年级上册中的“汉诺塔”问题（如图1）。

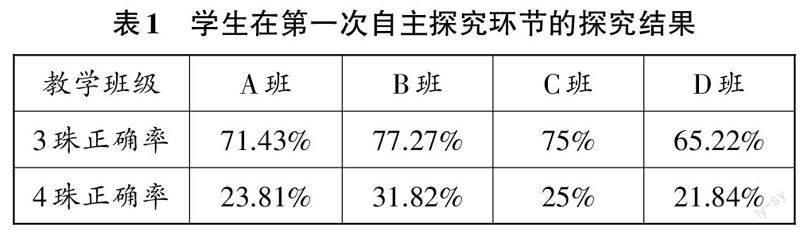
对于这个问题，笔者在不同学校给不同班级的学生讲授，并统计了学生在第一次自主探究环节的探究结果（见表1）。

回答正确的学生认为第一次选择对了杆，就比较节省时间，如果第一次选择错误了，就要再一次尝试。只有3个珠子时，移动的次数较少，一般通过一两次尝试都能成功，因此正确率相对较高。有4个珠子时，移动的次数多了，在移动的过程中，要选好杆，若选错了，就得从头再来，因此，有4个珠子时，正确率较低，耗费的时间较多。

又如，学生最开始接触“算24点”时，大都用已知数进行加、减、乘、除，以凑出结果。“用四则运算去凑出结果”成了学生唯一的解决问题的方法，这样的方式是耗时费力的。这样看来，思维方式会直接影响解决问题的效率。

二、原因分析

1.思维定式

学生在解决问题的过程中，最常用的是正向思维，即根据已知条件，通过假设法、尝试法等解决问题。这是学生惯用的思维方式，也是一种定式思维，定式思维一旦形成，若没有新的思维方式介入，就难以改变。

2.目标离心

学生在解决问题的过程中，总会被一些因素干扰而忘了最终目标。目标一旦不够明确，解决问题的道路就会又难又长。

三、结果导向型思维在课堂教学中的立论依据

1.以终为始，打破思维定式

结果导向型思维是一种逆向思维，即从最终的结果出发，反向分析过程或原因，寻找关键信息，找到解决问题的方法。用结果导向型思维思考问题，或许会使问题简单化。

2.少走弯路，提高解题效率

运用结果导向型思维思考，探求有效的解题策略和方法，能够提高解题效率。

3.全面剖析，提高解题正确率

运用结果导向型思维全面分析，是从结果倒推出解题步骤，是为寻找正确答案而做出的科学选择，这样的选择是有正确性保障的。

四、结果导向型思维在“汉诺塔”游戏教学中的范式应用

一个人要新建一种思维方式是不易的，因此载体的选择尤为重要。游戏是学生喜欢的娱乐项目，笔者认为，以数学游戏为载体建立结果导向型思维，不失为打开学生思维大门的好办法。

笔者将课堂作为渗透结果导向型思维的主阵地，以数学游戏“汉诺塔”作为教学内容进行了尝试教学。

1.充分试错，体会优势

在课堂教学中，学生是主体，教师应该扮演好组织者、引导者与合作者的角色。教师应做到“不愤不启，不悱不发”，只有在学生充分体验和尝试后仍无法解决问题时，再进行引导，才能让学生充分理解和接受所学知识。

要让学生体会结果导向型思维的优势，就先让学生感受固有思维方式的不足。在玩“汉诺塔”游戏的过程中，学生经过多次尝试，逐渐发现从一开始就要考虑第一个珠子往哪个杆移，运用尝试法非常耗时费力。在教师的引导下，学生感悟到，原来从结果出发，倒过来思考第一步，能少走很多弯路，就好像玩“走迷宫”游戏时，从出口倒着寻找路线会快一些。经过对比，学生充分感受到了结果导向型思维的优势。

【教学片段】

活动：3个珠子的移动。

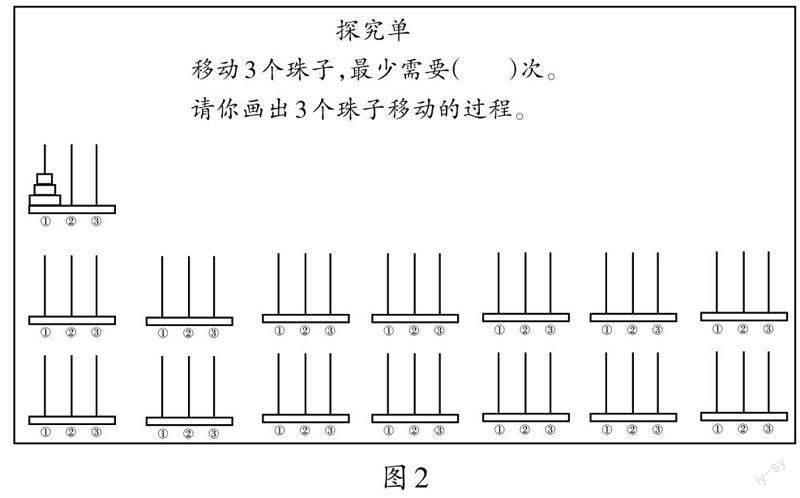
合作要求：（1）两人合作玩“汉诺塔”游戏，探究3个珠子最少需要移动几次；（2）达成一致后，一人移动珠子，一人将过程画在探究单（如图2）上；（3）合作时间为6分钟，完成后，可以再玩一玩“汉诺塔”游戏。

师（展示一张已完成的探究单，图略）：这张探究单上的内容有错吗？错在哪里？

生1：第一步就错了。

师：如何确定第一步？

生2：假设第一步像这位同学一样，先把最小的珠子移到②号杆，那中间有重复的移动过程，这样步数不是最少的。因此，第一步要先把最小的珠子移到③号杆，然后把中间的珠子移到②号杆，再把最小的珠子也移到②号杆，这样③号杆就空出来了，最大的珠子就可以移到③号杆了。

师：如果第一次尝试失败了，是不是就会耗费很多时间呢？你们静下心来想一想，有没有别的办法，不用尝试，就可以直接判断最小的珠子先往哪根杆移动呢？

生3：假如……

（学生依旧采用尝试法，只是这次是在脑子里想移动过程）

师：要使步数最少，你们觉得哪个珠子要尽快移到③号杆，才会最节省步数？

生4：最下面的珠子。

师：这样我们的目标就非常明确了，就是要让最下面的珠子尽快移到③号杆。现在该如何确定最小的珠子移到哪号杆呢？

生5：可以倒着想，目的是把最下面的珠子移到③号杆，那中间的珠子就要先移到②号杆，最小的珠子就要先移到③号杆。

师：这种倒过来想的思维叫结果导向型思维。

2.难度升级，巩固方法

要巩固新的思维方式，就要选择相关活动让学生在实践中充分体验感知，收获成功经验。由于移动4个珠子的思考方法与移动3个珠子的一致，難度升级的幅度也靠近学生的最近发展区，因此选择移动4个珠子来帮助学生巩固结果导向型思维较为恰当。

【教学片段】

活动：4个珠子的移动。

师：这次要先考虑哪个珠子呢？

生：最下面的珠子。把最下面的珠子尽快移到③号杆，就要把从下往上数的第二个珠子移到②号杆，把从下往上数的第三个珠子移到③号杆，把最上面的珠子移到②号杆。

师：看来，你们已经会用结果导向型思维来玩“汉诺塔”游戏了，大家都动手试一试吧。

不过，要让学生内化结果导向型思维，并将其熟练运用于“汉诺塔”游戏中，仅移动4个珠子是不够的。因此，还要安排移动5个珠子的活动环节。学生要对“汉诺塔”游戏有兴趣，并在课后对更多个珠子的移动进行实践和探索，才能将结果导向型思维深植于脑海。笔者多次教学后发现，学生会把“汉诺塔”当成日常游戏，课余时间，会三五成群地玩“汉诺塔”游戏。这样，在不知不觉中，结果导向型思维也就深入学生心中。

3.拓展延伸，用于生活

在课堂小结的环节，强调结果导向型思维不但适用于“汉诺塔”游戏，也适用于其他数学游戏和其他数学问题、生活问题，从而让学生树立运用结果导向型思维解决问题的意识，在学习、生活中能够主动去运用，很多问题就能迎刃而解。

【教学片段】

师：在哪些方面能用到结果导向型思维呢？

生1：在算“24点”时，我们也是从最终目标“24”出发，去思考如何将数字进行组合的。

生2：在玩“走迷宫”游戏时，从出口倒着寻找入口，更容易找到正确的路线。

师：在生活中会用到吗？

生3：开学时，老师都会让我们制定学习目标，然后我们就会从目标出发，为实现目标而不懈努力。

师：结果导向型思维不但可以运用于数学学习，还可以用来解决生活中的问题呢。

五、举一反三，灵活运用结果导向型思维

1.结果导向型思维在计算中的应用

在运算中，结果导向型思维是最为常见且被普遍运用的思维。比如，减法是加法的逆运算，除法是乘法的逆运算，学生最开始接触减法和除法的时候，就是“想加算减”或“想乘算除”，如算15-7=（    ），就会想（    ）+7=15；算63÷9=（    ），就会想（    ）×9=63。

通过逆运算得到答案，这就是运用了结果导向型思维，只是专业术语“想加算减”“想乘算除”“逆运算”等掩盖了结果导向型思维的本质。在计算教学中，教师可以让学生体验“想加算减”“想乘算除”是用结果导向型思维思考，以一法得通法。

2.结果导向型思维在解决问题中的应用

一般解决问题时会采用分析法，用分析法解决问题的思路分为以下几个步骤。

第一步，读题、收集数学信息。第二步，明确要解决什么问题。第三步，解决这个问题需要知道哪几个信息？它们之间有什么联系，为什么？第四步，接下来又要解决什么问题？需要知道哪几个信息？它们之间有什么联系？为什么？第五步，这样往下分析，直到把问题解决为止。

在解决问题的这些步骤中，最重要的就是“要解决这个问题需要知道哪几个信息？”这一思考过程，也就是从要解决的问题出发，倒过去找有用的信息，这样看，分析法的核心是结果导向型思维。这种解决问题的思路可以快速排除无关信息，有利于提高解决问题的效率。

3.结果导向型思维在图形与几何中的应用

图3是人教版教材二年级下册的“图形的运动（一）”第32页例4。该内容属于图形与几何领域，教材提供了尝试法解题思路。剪1个纸人：先对折，再画出半个图案。剪2个纸人：对折1次可以剪出1个纸人，对折2次就可以剪出2个。

笔者认为教学时可以不使用例题所呈现的方式，特别是要剪出4个手拉手的纸人，如果采用例题所给的方法，就比较复杂了。教师可以引导学生从最终要得到的4个手拉手的纸人出发，在脑海中想象把4个纸人的剪纸作品进行对折，对折1次可以剪出1个纸人，对折2次可以剪出2个纸人，因为纸人是左右对称的，所以需要再对折1次，也就是一共对折3次。于是，可以将一张长方形纸对折3次，然后在折痕处画上半个小人，为防止剪断，一定要将手脚朝向开口的地方，画的时候要“顶天立地”，这样就能剪出4个手拉手的纸人了。相比于例题所给出的方法，用结果导向型思维，显然节省了不少时间。

结果导向型思维在数学学习中广泛应用，对于很多数学问题，换一个角度思考，以终为始，可能会找到快捷的解决方法。但结果导向型思维往往与学生的一般思维方式相反，有些学生理解和接受起来有一定难度，要将其内化为自身的思维方式更有难度。这就需要教师在课堂教学中不断渗透，学生只有反复学习、巩固、运用，才能接受结果导向型思维，从而用它来解决更多数学问题。

另外，結果导向型思维不仅是在数学学习中非常有价值的思维方式，更是学生面向未来生活所需要的思维方式，因为结果导向型思维能让问题变得简单、明朗。一种思维方式的习得，不是简单的获取知识，而是获得一项技能，惠及终身，培养学生的结果导向型思维是面向未来的教学，是很有价值的！

［ 参 考 文 献 ］

[1］ 张奠宙，孔子坤，任敏龙，张园，殷文娣.小学数学教材中的大道理：核心概念的理解与呈现[M].上海：上海教育出版社，2018.

[2］ 余文森.核心素养导向的课堂教学[M].上海：上海教育出版社，2017.

[3］ 曹培英.跨越断层，走出误区：“数学课程标注”核心词的解读与实践研究[M].上海：上海教育出版社，2017.

[4］ 史宁中.基本概念与运算法则：小学数学教学中的核心问题[M].北京：高等教育出版社，2013.

[5］ 钱守旺.教好小学数学并不难[M].北京：北京大学出版社，2012.

（责编 黄 露）