基于几何设计法的航空发动机有限频域稳态抗扰控制器设计

陈佳杰，王继强，张海波，胡忠志，陈新民

1．南京航空航天大学 能源与动力学院，南京 210016

2．中国科学院 宁波材料技术与工程研究所 先进制造技术研究所，宁波 315201

3．清华大学 航空发动机研究院，北京 100084

巡航稳态工况一般为民航客机在整个飞行航线中时间最长的工况。飞机在保持长航时稳态工况的过程中，航空发动机会受到各种各样的内部和外部干扰。外部环境干扰主要包括雨雪冰天气干扰、大气湍流干扰和电磁干扰等。这些环境干扰会对发动机进口气流场造成影响，进而造成发动机内部部件性能参数不稳定；内部干扰主要包括传感器、执行机构等部件造成，以及旋转部件性能退化等。这些干扰对飞机保持巡航稳态的稳定性具有很大的隐患［1］。因此，稳态工况下的抗干扰问题一直是发动机控制的研究热点。

对于航空发动机在巡航工况下可能遇到的各类外界干扰，其能量一般只集中分布在某一个或某些有限的频率范围内，如果在抗扰控制器设计时忽略干扰信号自身的有限频域特性，设计的控制器往往具有较大的保守性。考虑到相同的干扰对发动机不同输出性能量的影响也不尽相同，理想的发动机抗扰控制器设计方法应具备以下特征：① 可以在任何特定频率或有限频域内定量表征抗扰控制性能指标；② 可以在不增加反馈信号传感器数目的情况下，对不同输出性能量进行全局抗扰性能的定量优化；③ 可以直观地在控制器设计阶段基于理论进行面向全局抗扰性能的控制器设计。

现阶段控制理论领域中，经典控制理论（PID、根轨迹法等）控制器设计方法核心是通过引入额外零极点来使闭环系统达到期望的频率响应特性，整个设计过程面向的是全频域，未能定义有限频域指标，也无法满足对不同输出性能量进行全局抗扰性能的定量优化要求［2］。主动抗扰控制理论主要包括基于干扰观测器的控制（DOBC）［3］和自抗扰控制（ADRC）［4-5］，虽然可以借助状态观测器估计干扰特性来在反馈回路中进行干扰补偿，但同样具有缺少控制器参数调节规范、无法直观定义有限频域内控制性能指标以及进行面向全局抗扰性能的控制器设计的不足之处。最优控制理论通常引入频率加权函数来优化有限频域性能，例如基于混合灵敏度的H∞控制方法［6-7］，但频率加权函数的选择大多数还是基于经验，需要反复尝试，而且基于频率加权函数的研究方法属于间接法，并不能提供被控对象在有限频域性能的定量信息。有限频Gramian 矩阵法［8］和广义KYP 引理法［9-10］是直接基于有限频域性能指标建立的控制理论，但同样无法同时满足这些特征，由于现有的有限频Gramian 矩阵法定义的是系统的H2性能，对于特定频率下的控制问题，有限频Gramian 矩阵为0，无法计算系统的H2性能。广义KYP 引理虽然可以在任何特定频率或有限频域内定量表征抗扰控制性能指标，但在设计控制器时由于需要额外引入权矩阵，导致了控制性能的保守性，并且对于不同的输出性能量也无法根据需求进行全局抗扰性能的定量优化。

考虑到上述控制方法对于解决有限频域抗扰问题的局限性，为了尽可能同时满足理想抗扰控制器设计方法特征需求，本文提出一种能同时具备这些特征的控制器设计方法“几何设计法”（Geometric Design Method，GDM）［11-12］。该方法目前已在振动控制以及能量收集领域取得了初步应用［13-14］，同时也为航空发动机稳态抗扰控制器的设计提供了一种新的思路方法和方向。对标理想发动机抗扰控制器设计方法的特征，几何设计法控制理论的创新点可归纳为以下3 个方面：① 聚焦有限频域内的抗扰性能进行控制器设计。几何设计法提供了一种系统的灵敏度直观整形方法，不引用依赖经验法则设计的加权函数，直观地建立了所设计的控制器与对应灵敏度函数频率特性的定量关系，从而可以方便地聚焦在特定频率或者有限频域内进行抗扰控制器设计，忽略其他不重要频域段的系统抗扰性能，大大降低了基于全频段性能指标进行抗扰控制器设计的保守性。② 定量进行全局抗扰性能“折衷”。在频域内寻求抗扰的“折衷”就是要求抗扰控制器在不同的频率范围内满足不同的性能指标，这就意味着需要充分考虑并利用系统本身及干扰的频率响应特性。几何设计法将不同输出量定义的性能指标通过坐标变换转化为复平面上的若干个性能圆，因而可以在特定频率或频域下定量分析各个性能量之间的可折衷性，以及进行满足需求的全局抗扰性能的“最优”“次优”控制器设计。③ 控制器设计过程的直观性。几何设计法最重要的创新点是在整个抗扰控制器设计过程中都能直观地在复平面上表示出闭环系统各输出量在特定频率下的抗扰性能，以及控制量在受限情况下的系统抗扰性能极限，从而使用直观的图解法形式来解决有限频域抗扰控制器的求取问题。

为了探究几何设计法在航空发动机稳态抗扰领域的应用前景，本文根据几何设计法控制理论，以某型先进齿轮传动涡扇（Gear Turbofan，GTF）发动机模型为基础，提出了基于几何设计法的航空发动机稳态抗扰控制器设计技术路线，并在频域和时域下分别研究了混合灵敏度H∞与GDM 控制器在巡航稳态工况马赫数干扰作用下的抗扰效果，初步验证了几何设计法所具有的实现上述抗扰控制特征的优势。

1 发动机建模及抗扰问题定义

本文所研究的发动机模型是一款30 000 磅（约合13.3×104N）推力级概念型GTF 发动机［15］，结构如图 1 所示，相比传统涡扇发动机，GTF 发动机的优势如下：

1） 低压轴和风扇轴通过齿轮箱连接，使得风扇可以在理想的低转速下工作的同时可以保持低压轴的高速旋转，解决了风扇和低压压气机不能同时在各自最佳转速下工作的问题，提高了燃料效率并降低了燃气轮机噪声。

2） 引入了可变放气活门（Variable Bleed Valve，VBV）来防止低压压气机失速，以及风扇外涵可变面积尾喷口（Variable Area Fan Nozzle，VAFN）来保证风扇在各个工作点保持最佳效率，这2 个控制变量根据相应的调度计划开环计算得到，不参与主回路控制。

GTF 发动机部件级模型基于NASA 开源的热力学系统建模和分析工具箱［16］建立，除不包括起动模型外，适用于在全飞行包线进行仿真。模型中主燃油控制回路中的控制量为燃油流量，被控量为与推力线性相关度强的风扇折合转速。

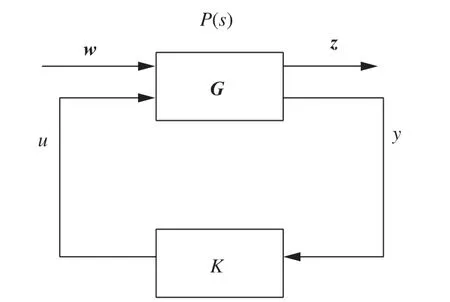
图2 标准反馈控制结构Fig. 2 Standard feedback control structure diagram

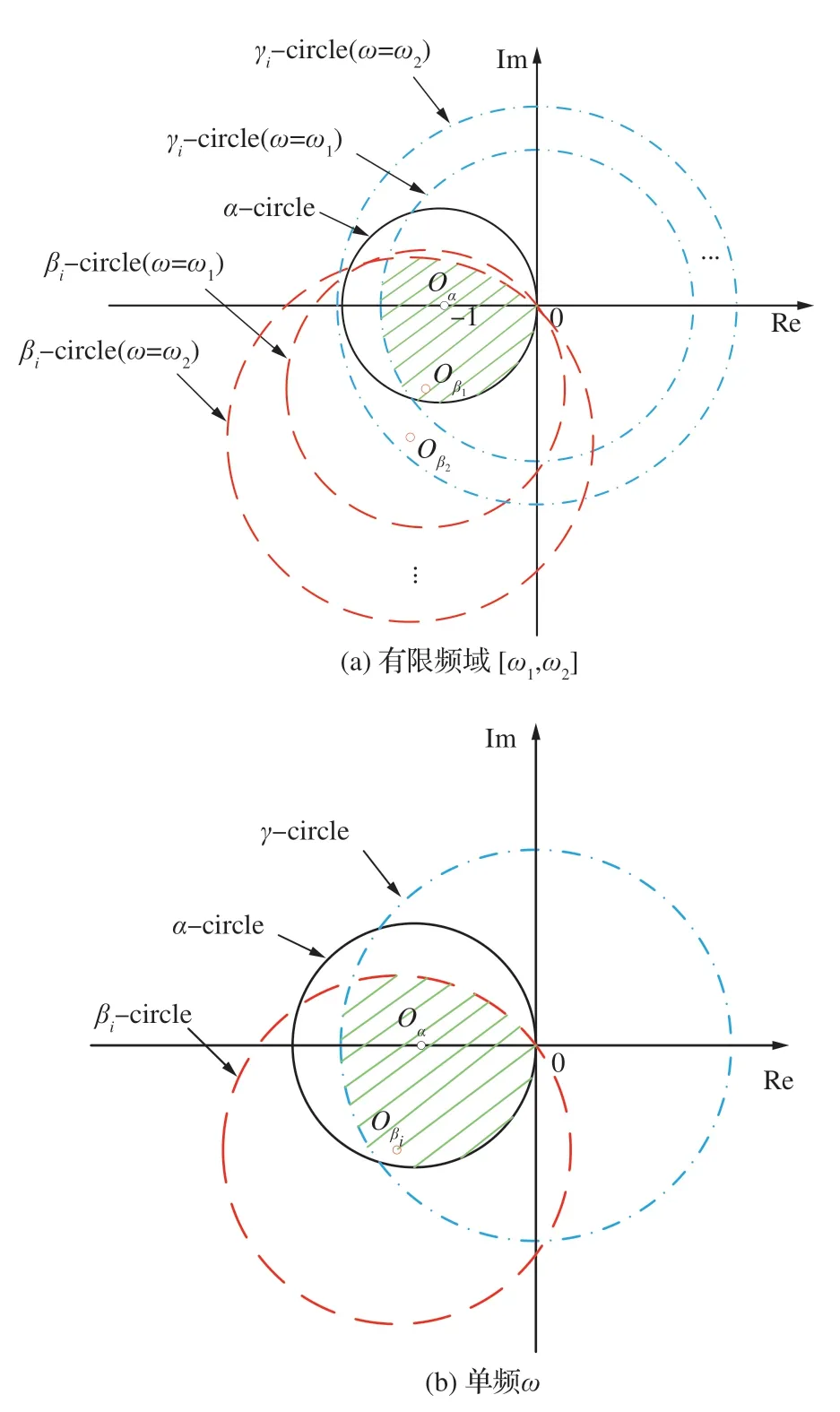
图3 几何设计法存在性问题在复平面上示意图Fig. 3 Geometric design method schematic diagram in complex plane

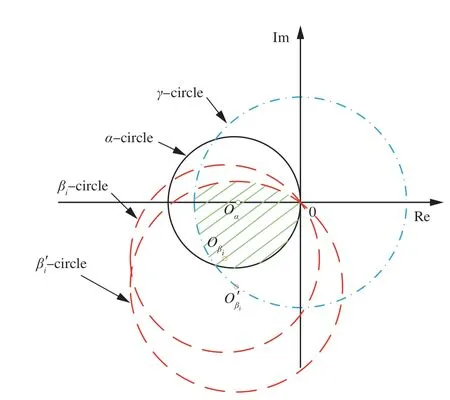
图5 复平面上对应的鲁棒控制器设计区域Fig. 5 Robust controller design scope in complex plane

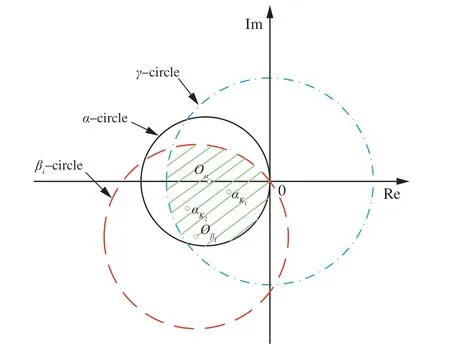
图6 复平面上不同控制器性能比较Fig. 6 Different controller performances described in complex plane

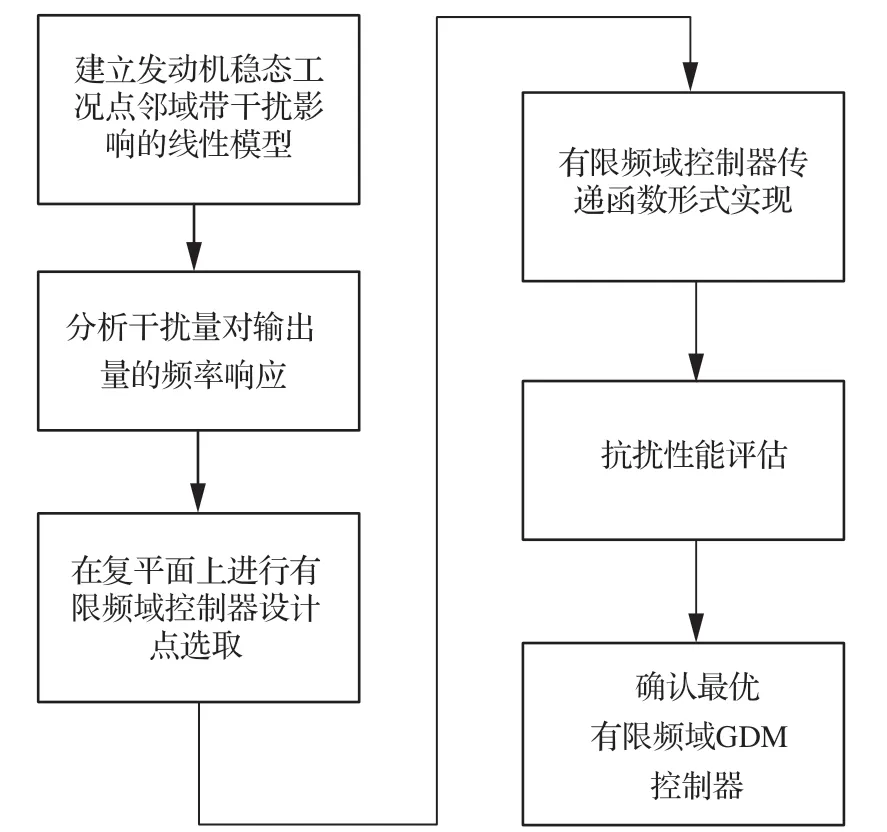
图7 GDM 控制器设计流程Fig. 7 GDM controller design process

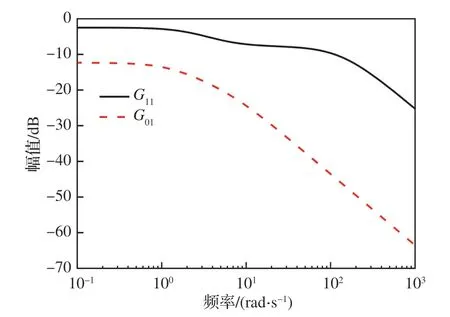
图8 干扰对系统输出的幅频特性分析Fig. 8 Frequency domain analysis of transfer function from disturbance to outputs

本文研究的抗扰问题可以定义为，GTF 发动机在飞机巡航段长航时稳态飞行的情况下，会受到大气湍流带来的马赫数干扰［17］，这会造成表征推力的风扇折合转速的波动，然而实际发动机推力和风扇折合转速的频率特性并不相同，仅进行风扇折合转速的抗扰控制器设计无法同时考虑到该控制器对推力的抗扰特性。因此，抗扰问题定义为设计一种主燃油控制回路的抗扰控制器，使得能在大气干扰能量集中的有限频域内，风扇折合转速和推力均有较好的综合抗扰性能，且尽可能地挖掘抗扰性能极限。

2 几何设计理论介绍

几何设计法的理论基于标准反馈控制结构，如图 2 所示。

广义被控对象P的传递函数矩阵可表示为

式中：

u表示控制量；w中变量表示外部输入信号，包括各类干扰信号；y表示可用的反馈信号；z中变量是可控性能变量但不能用于反馈输出。因此，设计目标是仅使用u=Ky反馈来控制整个结构系统，即达到对所有性能变量y和z的控制。虽然z不可用于反馈，但是可以假设在调试或建模阶段可获得传递函数矩阵G。

为了方便进行控制器设计，进一步假设输入信号wi(jω)=Cid(jω)。其中，ω表示频率；Ci是相对于单位输入信号d(jω)的复数增益；i=1，2，…，n。由此式（1）可写为

单位输入信号d到输出反馈信号y以及可控性能变量信号zi的传递函数为

单位输入信号d到输出反馈信号y以及可控性能变量信号zi的开环响应为

几何设计法原理致力于在特定频率点或有限频域定义出性能极限的能力。对于特定频率点ω或有限频域[ω1，ω2]， 控制问题被重新定义为寻找控制器K，使得所有性能变量Tyd_c和(i=1，2，…，n) 在频率ω处或有限频域[ω1，ω2]上按相应抗扰性能需求衰减。这个问题包括存在性、最优性和控制综合鲁棒性3个子问题：

1） 存在性问题：仅使用u=Ky同时减少y(jω)和zi(jω)的可实现性。

2） 最优性问题：y(jω)和zi(jω)的最优性能。

3） 控制综合鲁棒性问题：针对给定全局抗扰性能指标，设计并实现强镇定控制器K(s)，并且对于被控对象的内部不确定性，K(s)具有鲁棒性。

为方便后续描述，定义灵敏度函数S、反馈灵敏度函数α及扰动灵敏度函数βi：

式中：

为表征控制器K作用后的抗扰性能，定义输出量的性能指标η为输出量闭环幅值和开环幅值之比，由式（3）～式（7）可得：

式中：δ1、δi为性能指标的需求，可根据实际抗扰需求进行更改。

控制器K的选取决定了反馈灵敏度函数α(jω)在复平面上的坐标，定义性能圆和控制量限制圆如下：

1） 性能圆（α、β圆）

由式（7）可得，满足性能指标的α(jω)所在区域可以在复平面表示为以（-1，0）为圆心，δ1为半径的圆，记作α圆，将δ1为1 的圆记作单位α圆。

2） 控制量限制圆（γ圆）

本文所研究的控制量燃油流量有很多限制，包括喘振、熄火边界、涡轮前最大温度、转速、压力等。巡航稳态工况下，定义控制量的范围为

对于本文的控制问题，可转化为

式中：us为稳态工况点对应的燃油流量。由u=Ky得

进而可得

限制圆体现在复平面上即为以（0，0）为圆心，半径为rγ的圆区域内。

因此，特定频率及有限频域[ω1，ω2]内的受限抗扰控制问题的存在性和最优性问题便可通过图形法来解决。针对引言给出的理想的抗扰控制器特征，分别提出命题如下。

命题1（存在性问题）当且仅当所有性能圆（α、β圆）和限制圆（γ圆）具有共同交点时，存在控制器u=Ky使得性能指标ηyd及同时减少。如图 3 所示，图 3（a）和图 3（b）的阴影区域分别表示特定频率及有限频域[ω1，ω2]下使得性能指标ηyd及ηzid同时减少的控制器设计点α(jω)所在区域。

命题2（最优性问题）若存在一组δopt，δi_opt，使得性能圆（α、β圆）相切，且相切点位于限制圆（γ圆）内，则位于性能圆圆心连线所在直线上的相切点αopt所对应的控制器为该频率下使得性能指标ηyd及能获得最优全局抗扰性能的控制器，最优全局抗扰性能ηyd_opt及的分布满足

式中：L代表两点之间的距离。各抗扰性能指标（单位：dB）的几何表达形式为

最优性/次优性问题的几何设计图如图 4所示。

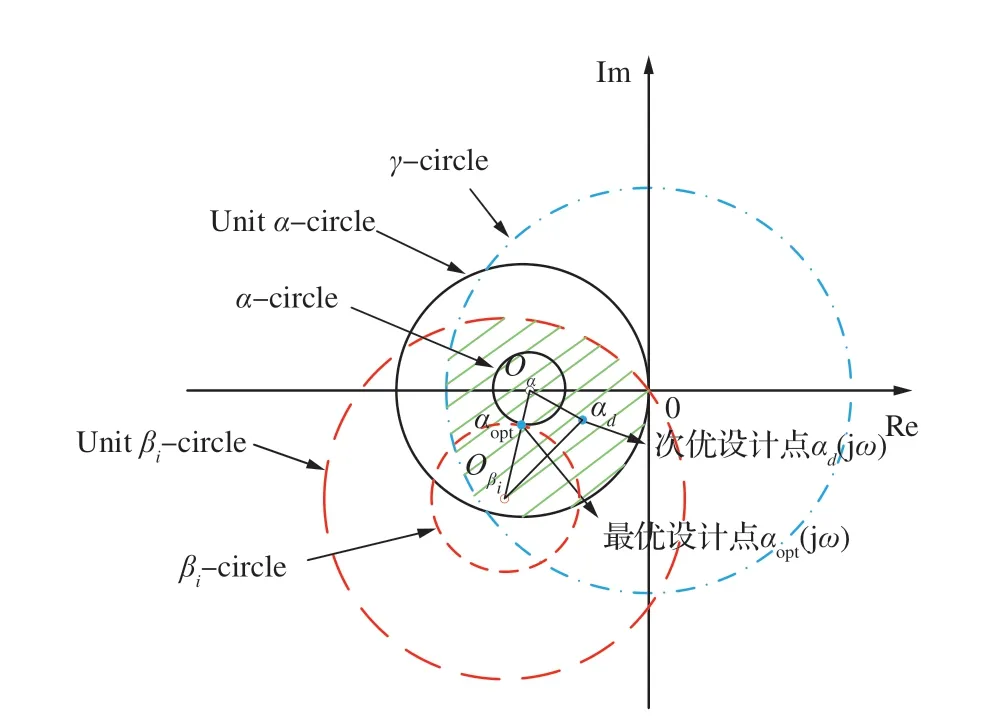
命题2 备注1δ1、δi决定了性能圆的半径，式（15）直观地构建了复平面上各输出量的最优抗扰性能指标的几何表达形式。根据性能圆圆心与控制器设计区域的位置关系，可分为如下4 种情况讨论：

1）Oα和均位于控制器设计区域时，最优设计点αopt分别与Oα和重合时，则ηyd和分别具有极限抗扰性能。

2） 仅Oα位于控制器设计区域时，极限抗扰性能对应的最优设计点αopt位于与单位α圆的交点。

4）Oα和均不位于控制器设计区域时，极限抗扰性能对应的最优设计点αopt位于与单位α圆的交点；ηyd极限抗扰性能对应的最优设计点αopt位于与单位βi圆的交点。

命题2 备注2式（14）构建了复平面上各输出量的最优抗扰性能指标的约束关系，用于直观地描述系统所能达到的最优全局抗扰性能，由式（14）可知不同αopt坐标对应不同的最优全局抗扰性能，η越小代表抗扰性能越好。

命题2 备注3由于在实际工程中，最优全局抗扰性能可能存在无法实现的情况。可以根据实际控制需求合理调整全局抗扰性能指标，设计次优控制器。如图 4 所示，根据三角形边长几何关系大小可得

次优全局抗扰性能ηyd及的分布满足

各次优抗扰性能指标同样满足式（15）的几何表达形式。

命题3（鲁棒性问题）对于被控对象内部的不确定性对抗扰控制性能的影响，可转化为性能圆βi圆的变化，如图 5 所示，具有鲁棒性的控制器设计区域缩小为阴影部分区域。

命题3 备注1假设被控对象内部的不确定性对Gi造成的乘积摄动为

β′i圆以Gi′(jω)为圆心，|为半径，βsup为稳定裕度，当时，图 5 中不存在鲁棒控制器设计区域。

命题4（控制综合问题）设计点α(jω)的复平面坐标可通过式（19）来构造相应控制器：

并可根据实际需求进一步实现控制器K的数学表达式，如传递函数表达式等。

命题4 备注1可以通过如下的构造法［18］，将设计点α(jω)的复平面坐标转化为强镇定控制器传递函数表达式K（s），使得K（s）在频率ω下的表达式K(jω)满足式（19）。

假设设计点α(jω) 对应的灵敏度函数S(jω)=α(jω)-1=a+bj，a和b同号，以下分别从同正和同负为例进行构造。

1）a、b均为正数

2）a、b均为负数

定义，同理可构造

式中：

其中：A＞0，c＜0，d＞0。相应的强镇定控制器传递函数形式表示为

式中：σ是一个小的正数，用于将控制器的极点移到左半平面，σ越小，K（s）在设计频率ω处越近似于K(jω)。

a和b一正一负的2 种情况可同理进行构造。若构造出的传递函数阶数较大，可进行降阶处理。

命题4 备注2对于在有限频域[ω1，ω2]内求解控制器K的问题，可以通过如下简化方式进行设计：

1） 在[ω1，ω2]取N个频率点，在图 3（a）所示控制器设计区域中依据命题2 选取合适的设计点α，分别采用命题4 备注1 的方法构造对应的控制器Kp，p=1，2，…，N并实现。

2） 比较不同单频控制器传递函数在有限频带[ω1，ω2]上的频率特性，选择频率特性最优的单频控制器作为有限频带[ω1，ω2]内的控制器K。

命题5（不同控制器抗扰性能对比问题）对于给定输入输出传递函数类控制器K（s），可以得到K（s）在特定频率ω下对应的复平面点α(jω)表达式：

命题5 备注1通过几何图示可以直观地比较不同输入输出传递函数类控制器（例如PID 控制器、混合灵敏度H∞控制器等）的抗扰性能，如图 6 所示，和分别表示不同控制器K（s）所对应的复平面点，不同控制器作用下闭环系统各输出量的抗扰性能可根据式（15）的原理直观地从几何图上得到。

3 GDM 抗扰控制器性能仿真分析

本节针对第1 节定义的发动机典型抗扰问题，对巡航稳态工况下GTF 发动机的抗扰控制器进行设计及仿真验证。抗扰控制器设计及仿真分析流程的总结如图 7 所示。

3. 1 GTF 巡航点邻域带干扰影响的线性模型

GDM 控制器需要基于发动机的线性化模型进行设计。基于2.1 节介绍的GTF 发动机部件级模型，采用小扰动辨识法得到巡航包线内某稳态工作点（H=28 000 ft，Ma=0.73， PLA=83.4°，1 ft=0.304 8 m）邻域的传递函数矩阵模型为

式中：

式中：Nfc、F、Wf和Ma分别代表归一化风扇折合转速、推力、燃油流量以及马赫数干扰的增量。

3. 2 干扰量对输出量的传递函数频域分析

干扰量的频率特性研究是GDM 抗扰控制器设计的关键。分析马赫数干扰对转速和推力的开环频率响应如图 8 所示。可以看出，在0～10 rad/s 内，转速和推力幅频特性变化基本一致；但10～100 rad/s 内，对于该频率段下的干扰信号，转速的波动将呈现较大的衰减，但推力波动没有。对于100 rad/s 后的干扰，2 者的波动均呈现较大衰减，有较强的滤波能力。根据文献［19-20］提出的大气湍流干扰模型的原理，可以取谐波输入信号为

将得到的归一化输入马赫数干扰信号进行傅里叶变换，如图9 所示。结合图 8 和图 9，本文选取ω在2～16 rad/s 的有限频域进行抗扰控制器的设计研究。

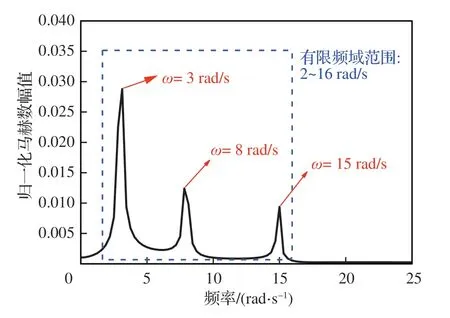
图9 归一化马赫数干扰的频谱分析Fig. 9 Normalized Mach number disturbance spectrum

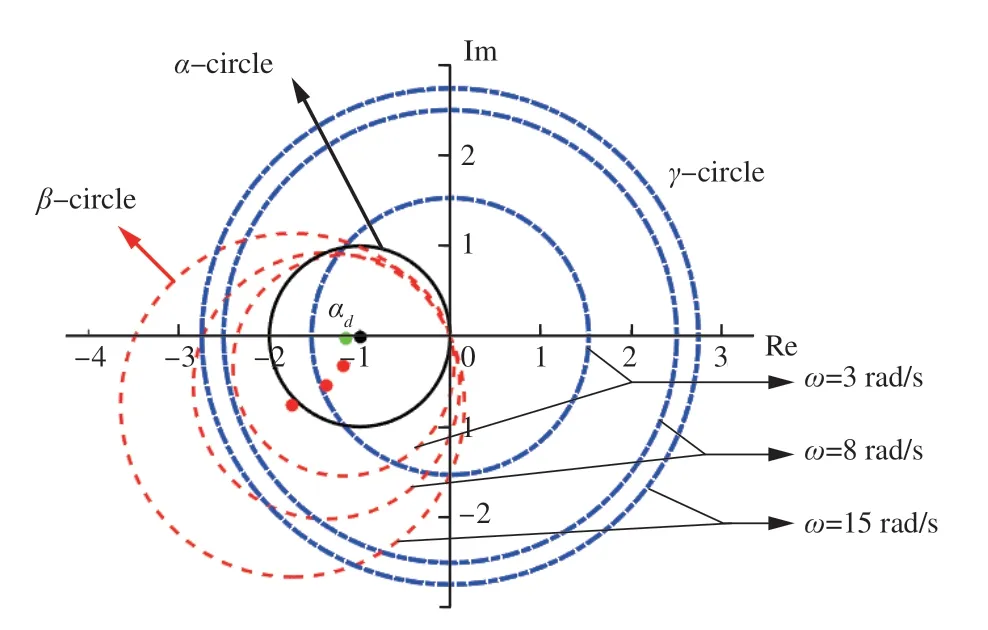
图10 复平面上GDM 控制器设计区域Fig. 10 GDM controller design area on complex plane

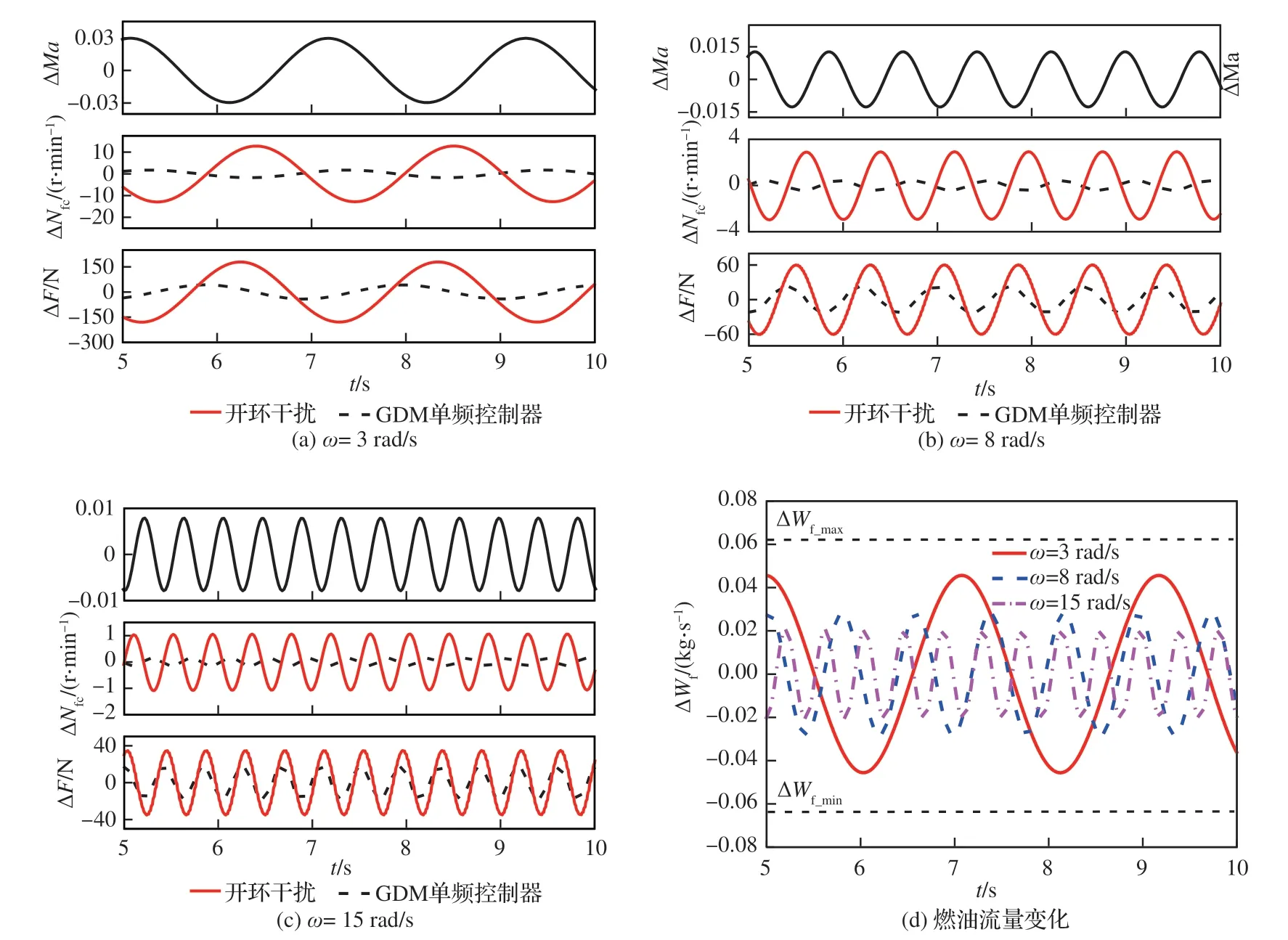
图11 不同频率下GDM 单频控制器的抗扰性能Fig. 11 Disturbance rejection performance of GDM controller under different single frequency

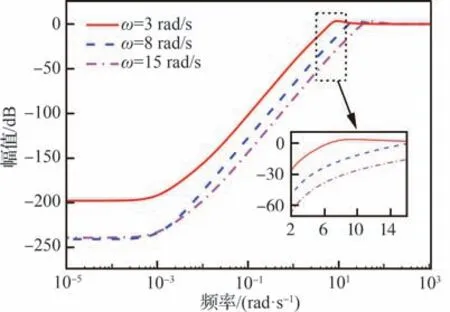
图12 不同GDM 单频控制器作用下ηyd 在有限频域的幅频特性Fig. 12 Comparison of ηyd frequency domain characteristics among different GDM controllers

3. 3 GDM 抗扰控制器设计及抗扰性能验证

首先进行单频抗扰控制器设计。根据命题1，分别在频率点3、8、15 rad/s 处在复平面上进行几何分析，并根据命题3 和命题4 选取合适的α点进行次优控制器实现，如图 10 所示。

根据命题2 分析图 10 可得，在α圆心左侧且位于3 个频率下所有圆交集区域内取设计点，可以得到全局抗扰性能较好的次优控制器。以设计点α坐标为（-1.15，-0.02）为例，由式（15）可得设计点不同频率下对应不同输出量的设计抗扰性能指标，如表 1 所示。

为验证表 1 直观在图 10 中得到的各输出量抗扰性能指标的准确性，在时域中进行仿真算例如下。首先，根据命题4 传递函数构造法实现相应GDM 控制器并统一降阶至易于实际使用的三阶，假设在单位正弦马赫数干扰作用的情况下，各频率下GDM 控制器的闭环系统输出扰动量如图 11 所示。降阶后不同频率下各GDM 控制器传递函数以及从图 11 得到的实际抗扰性能汇总在表 2。可以看出，降阶后GDM 控制器传递函数在各自设计频率下所对应的α(jω)略有偏差，实际抗扰性能基本达到表 1 从图 10 上直观得到的设计抗扰性能指标；从图 11（d）可以看出图 10 中的限制圆也有效地限制住了由于抗扰控制器的引入所带来的燃油流量的变化。仿真结果初步验证了理想抗扰控制器设计方法的特征1～特征3。

其次，进行有限频域内抗扰控制器设计。选择由式（28）所示谐波信号作为大气湍流干扰模型的输入得到的马赫数干扰信号，来作为发动机模型的干扰输入，从图 9 可知，马赫数干扰能量集中在有限频域2～16 rad/s。比较不同GDM 单频控制器在有限频域下的控制性能指标ηyd和ηzd的频率特性，分别如图 12 和图 13 所示。由图 12 可见，ω=15 rad/s 的控制器在有限频域2～16 rad/s 相比其他2 个单频控制器具有更好的折合转速抗扰控制性能。由图13 可见，各个单频控制器在设计频率前具有较好的抗扰性能，但在设计频率之后抗扰性能开始快速恶化，这符合几何设计法的原理，考虑在2～16 rad/s 的频率段确定综合被控量和性能量抗扰性能最佳的控制器，初步选择在ω=15 rad/s设计的单频控制器作为GDM 宽频控制器。为进行进一步验证，不同单频控制器在时域下抗扰性能仿真验证结果如图14 和图15 所示。

表1 不同频率下控制器设计点所对应的性能指标ηyd 和ηzdTable 1 Design ηyd and ηzd under different single frequency

表2 不同频率下GDM 控制器传递函数实现形式及所对应的实际抗扰性能Table 2 Realistic performances and transfer functions designed by GDM under different single frequency

表3 不同GDM 单频控制器在时域下稳态抗扰性能对比Table 3 Comparison of disturbance rejection performances among GDM controllers designed in different frequency

表4 不同巡航稳态工况下稳态控制器的抗扰性能比较Table 4 Comparison of controller disturbance rejection performance under different cruise steady-state points

图13 不同GDM 单频控制器作用下ηzd 在有限频域的幅频特性Fig. 13 Comparison of ηzd frequency domain characteristics among different GDM controllers

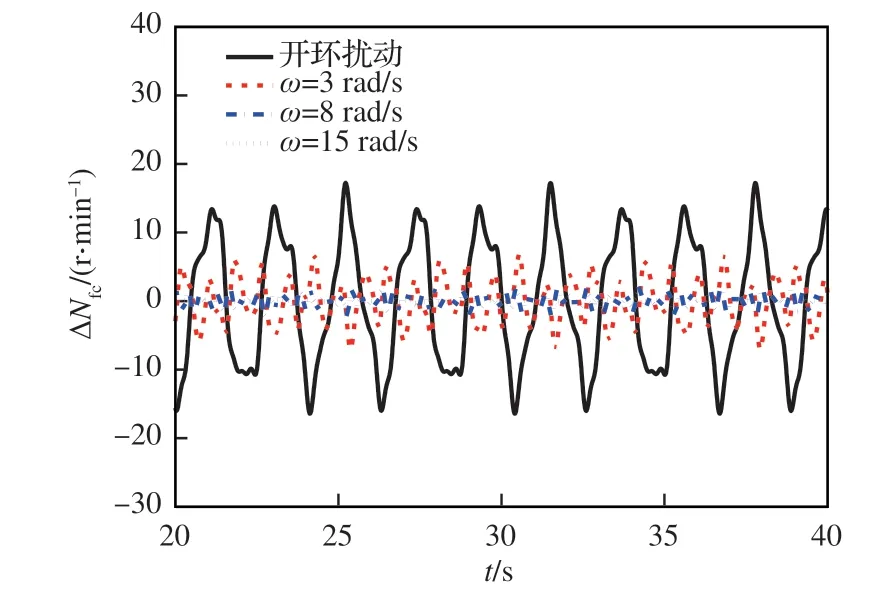
图14 不同GDM 单频控制器作用下风扇折合转速的稳态扰动性能变化Fig. 14 Time domain characteristics of corrected fan speed under different GDM controllers

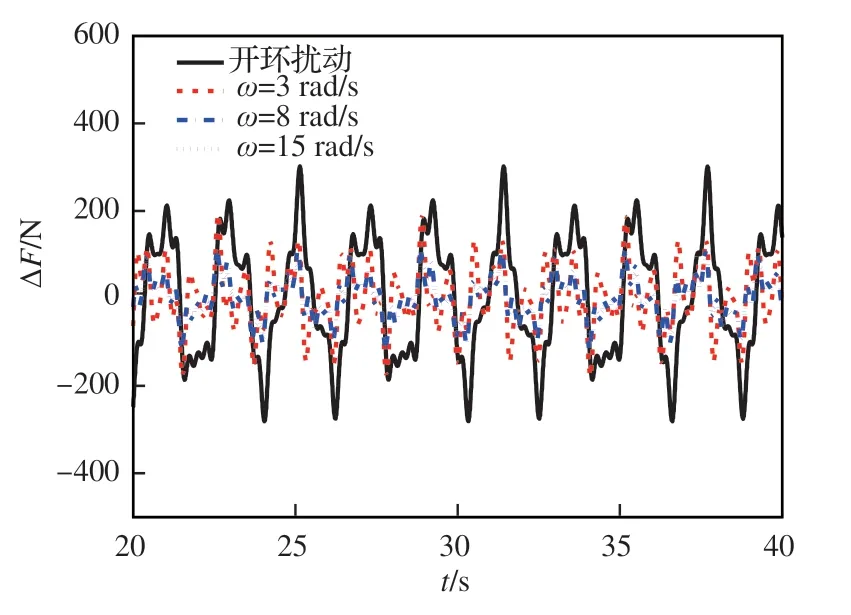
图15 不同GDM 单频控制器作用下推力的稳态扰动性能变化Fig. 15 Time domain characteristics of thrust under different GDM controllers

图16 混合灵敏度H∞控制器权函数及Tzw的频率特性Fig. 16 Frequency characteristics of weight function and Tzw in mixed sensitivity H∞ controller

为了更好定量地在时域下评估不同控制器的抗扰性能，定义性能量抗扰百分比J为

式中：qc_max和qo_max分别为相同干扰输入时，闭环控制器作用下与开环作用下输出量的最大扰动量。各GDM 单频控制器闭环作用下对被控量折合转速Nfc和性能量推力F的抗扰性能定量结果如表 3 所示。仿真结果表明，ω=15 rad/s 设计的单频控制器具有接近性能极限的折合转速抗扰百分比以及最高的推力抗扰百分比，可作为最终选定的GDM 控制器用于GTF 发动机巡航工况下马赫数干扰的有限频域抗扰控制器。

3. 4 混合灵敏度H∞与GDM 控制器有限频域抗扰性能对比

采用3.3 节设计的GDM 控制器与发动机常用的混合灵敏度H∞控制器进行有限频域抗扰性能对比。混合灵敏度H∞控制器设计过程参考文献［2］，定义在全频域的闭环传递函数的H∞指标为

混合灵敏度加权函数W1和W3构造过程为

式中：εα和εS为加权灵敏度函数矩阵的调节因子；εβ和εT为加权补灵敏度函数矩阵的调节因子；ωB为闭环系统设计带宽。 本研究中取ωB=3 rad/s，εS=0.2，εT=0.2，εα=0.1，εβ=0.1。通过求解式（30）的次优H∞问题，可以得到p为0.102 0，加权函数的频率特性图以及Tzw的奇异值特性如图 16 所示。可以看出，混合灵敏度H∞控制器使得Tzw的H∞范数指标在全频域范围内小于0.102 0（-19.83 dB），保证了全频域范围内的抗扰性能，但在有限频域抗扰问题上具有一定的保守性。

对比混合灵敏度H∞和GDM 控制器抗扰性能指标ηyd和ηzd的频率特性，如图17 和图18 所示。可以看出，GDM 控制器即便在其他部分频域段的系统抗扰性能不如混合灵敏度H∞控制器，但在发动机巡航抗扰所关注的有限频带2～16 rad/s 上，GDM 控制器作用下系统的抗扰性能得到显著提升。

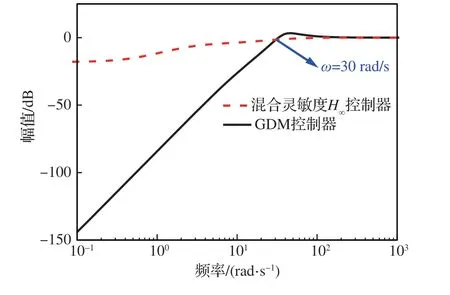
图17 混合灵敏度H∞与GDM 控制器作用下ηyd 在有限频域的幅频特性Fig. 17 Comparison of ηyd frequency domain characteristics between H∞ and GDM controller

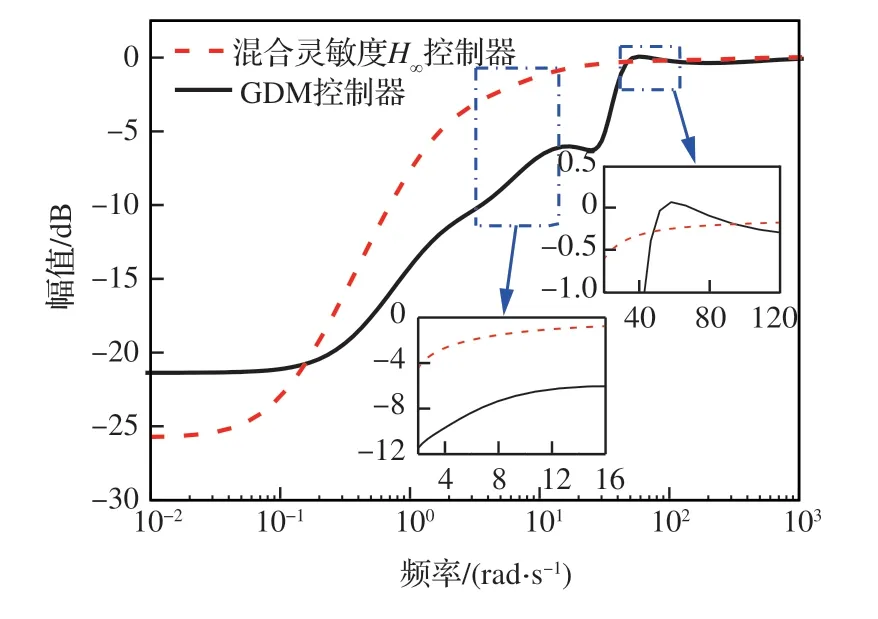
图18 混合灵敏度H∞与GDM 控制器作用下ηzd 在有限频域的幅频特性Fig. 18 Comparison of ηzd frequency domain characteristics between H∞ and GDM controller

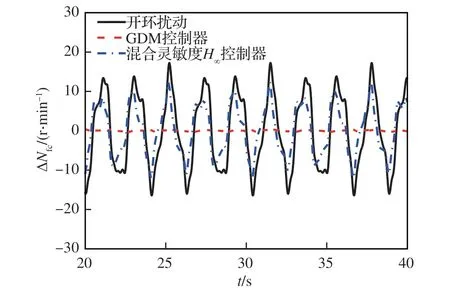
图19 混合灵敏度H∞与GDM 控制器作用下风扇折合转速的稳态扰动性能变化Fig. 19 Time domain characteristics of corrected fan speed under H∞ and GDM controllers

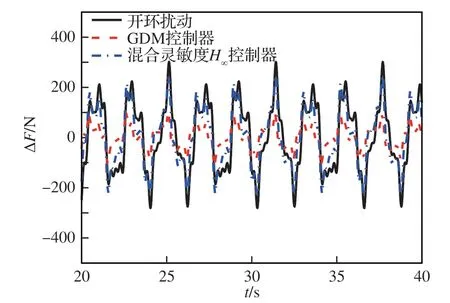
图20 混合灵敏度H∞与GDM 控制器作用下推力的稳态扰动性能变化Fig. 20 Time domain characteristics of thrust under H∞ and GDM controller

在相同马赫数干扰作用下，混合灵敏度H∞控制器和GDM 控制器的抗扰仿真验证结果如图 19 和图 20 所示。混合灵敏度H∞控制器的Nfc抗扰百分比和F抗扰百分比分别为29.8% 和17.6%，远小于表 2 中GDM 控制器97.7%的Nfc抗扰百分比和66.7%的F抗扰百分比，论证了频率特性图 16 和图 17 分析结果的准确性。

为进一步验证该GDM 抗扰控制器的设计流程的适用性，另取GTF 发动机巡航包线下2 个稳态工况点，采用图 7 的设计流程进行抗扰控制器设计，结果如表 4 所示。可以看出，采用几何设计法设计的抗扰控制器相比混合灵敏度H∞控制器，风扇折合转速抗扰百分比提升30%以上的同时，推力抗扰百分比提升了15%以上，全局抗扰性能有显著提高，基于几何设计法的稳态抗扰控制器具有普遍适用性。

4 结 论

首先建立大涵道比齿轮传动涡扇发动机部件级模型，针对传统的混合灵敏度H∞抗扰控制方法缺少在控制需求指定频率ω0或有限频域[ω1，ω2]上定义出性能极限的能力，提出了一种可以在任何关注频率或有限频域上进行性能改进的通用方法“几何设计法”，定义出基于几何设计法的航空发动机抗扰控制器设计路线，为航空发动机稳态抗扰控制器的设计提供了一种新的思路方法和方向，并在频域和时域上进行了分析和仿真验证，结果表明：

1） 几何设计法相较于传统抗扰控制器设计方法，通过参数的转化代换从而使控制器选取范围在复平面坐标系中体现为圆的交集，具有直观性。可以满足理想的发动机抗扰控制器设计方法应具备的特征。

2） 针对扰动分量集中在ω∈[2，16] rad/s 的有限频域马赫数干扰，由于几何设计法的抗扰控制原理相较于混合灵敏度H∞控制更直观地定义了特定频率和有限频域内控制器对闭环系统输出量的抗扰性能，采用几何设计法设计的抗扰控制器相比混合灵敏度H∞控制器，折合转速抗扰百分比和推力抗扰百分比均有显著提高。