带有输入受限的无人机精确编队合围容错控制
2023-06-28西北工业大学自动化学院西安710129
西北工业大学 自动化学院,西安 710129
刘伯健,李爱军,郭永*,王长青
无人机分布式协同控制具有高复杂性、高自主性和高智能性等特征,是未来战争中的重要技术。因此,诸多学者对无人机分布式协同控制进行了深入研究,并根据领航者的数量将其分为单领航者、多领航者和无领航者3 类。单领航者协同控制中,基于一致性理论的控制方法应用最为广泛,该方法使无人机群易于形成精确编队[1-3]并且可以更好地处理无人机非线性动力学带来的约束和不确定动态[4]。无领航者协同控制的主要解决方案多是由人工势函数方法发展而来,通过该方法的固有特性可以轻松处理避障和机间避碰问题[5],并易于实现自组织和自适应功能[6]。合围控制作为多领航者协同控制中的一种重要算法,其主要特点是使跟随者能最终收敛到领航者们所形成的凸包络内[7],该特点可以使无人机群在避开危险区域的基础上保持广义的编队构型。
与单领航者和无领航者编队相比,关于多领航者编队控制的研究相对较少。合围控制的早期研究多是针对多智能体系统展开的,其领航者被认为是静态的[8]。后来为了适应领航者的运动特性,提高算法的适用范围,学者们又提出了针对动态领航者的合围控制协议[7,9]。此后,随着无人机协同控制算法的不断发展,领航者间相互通信并且形成期望队形的“编队-合围”控制算法受到了大量关注[10-11]。该算法通过分层架构首先控制领航者形成某一预设凸包络队形,再通过合围控制使跟随者收敛到该凸包络内,最终实现一种广义的编队跟踪控制。该广义编队只要求跟随者收敛到领航者所形成的凸包络中,却没有考虑跟随者最终在凸包络内的位置和其所形成的形状。这使合围控制在大规模编队的情况下,很容易引发机间碰撞等问题。
由于编队飞行对多无人机控制系统的安全性、可靠性和准确性提出了更高的标准和要求,容错控制成为近年来学者们的研究热点。其主要方法可分为基于故障诊断的主动容错技术[12]和基于提升控制系统鲁棒性的被动容错技术。被动容错技术被广泛应用于无人机协同控制领域,其主要方法包括基于自适应的容错方法[13-15]、基于观测器的容错方法[16-18]和基于人工智能的容错方法[19]等。文献[15]提出了一种自适应方法来处理无人机的作动器故障,其系统的收敛性与作动器的故障系数显性相关。基于观测器的容错控制是应用最为广泛的技术,例如误差观测器[16]和扩张状态观测器[17-18]。其中,观测器的设计方法有很多,例如径向基函数神经网络(Radial Basis Function Neural Network, RBFNN)观测器[19]、滑模观测器[20]和高增益观测器[21]等。虽然基于观测器的容错控制效果相对较好,但是由于需要额外设计观测器结构,因此增加了控制系统的设计难度和结构的复杂度。此外,随着人工智能的发展,许多学者直接采用神经网络或模糊系统对无人机故障产生的非线性动态进行拟合,并取得了一定成果[19]。
近年来,输入受限问题在理论和工程实践中被逐渐重视。如果在控制器设计过程中忽视该问题,则会使控制器的控制效果在实际控制中存在弱化,甚至会破坏整个系统的稳定性。因此,学者们提出了多种方法来解决该问题。一种方法是通过中值定理结合自适应方法对受限的输入信号进行处理[22-23];还有学者提出了通过辅助系统进行信号补偿的方法处理输入受限问题[24];文献[25]通过设定受限指标参数并结合自适应方法对输入受限问题进行了处理。虽然上述方法为解决输入受限问题提供了很多思路,但其稳定性证明被指出存在不严谨的地方[26-27]。此外,受到未知输入方向问题的启发,文献[28]将Nussbaum 函数用于处理输入受限问题,给该问题的解决带来了新的启发。
针对上述挑战,本文研究了多无人机在存在输入受限、外界干扰和作动器故障的情况下的有限时间精确编队合围控制问题。最终的控制目标是使所有跟随者在输入受限、外界干扰和作动器故障的情况下,在有限时间范围内,收敛到领航者所形成的凸包络内,并且在其中形成预设的精确队形。本文的主要创新点有:① 提出了一种基于预设队形的合围控制通信拓扑权重设计方法,与传统合围控制相比,该拓扑不仅能使跟随者收敛到领航者所形成的凸包络内,而且能使跟随者在其内部形成精确的预设编队;② 提出了一种新颖的光滑函数对非对称输入受限信号进行平滑处理,与传统双曲正切函数相比[28],其拟合误差可以通过参数控制,使系统误差收敛到原点附近更小的邻域内;③ 提出了一种基于Nussbaum 函数的有限时间自适应合围控制器,将该控制器与本文的光滑函数结合,可以同时处理输入受限和作动器故障问题。
1 问题描述
在本文中,Rn×m表示n×m的矩阵;‖· ‖表示欧几里得范数;z[k]表示向量z的第k个元素;[Y]i∈R1×n和[Y]i∈Rm×1分别表示Y∈Rm×n矩阵的第i行和第i列;⊗表示克罗内克积;λmax(Y)和λmin(Y)表示矩阵Y的最大和最小特征值。此外,为了方便公式推导过程中的表示,定义,其中函数。
1. 1 Nussbaum 函数及引理
定义1[28]Nussbaum 函数是一个连续函数并且满足如下特征:
引理 1[28]考虑V和χi都是定义在[0,tf)上的连续函数,对于t∈[0,tf),存在V(t)>0 且N(χi)是关于变量χi的Nussbaum 类型函数。如果下述内容中的式(2)成立,那么V、χi和在[0,tf) 上都有界。
式中:c>0;γτi>0;c0>0;ξτi>0。
引理 2[19]考虑系统ẋ=f(x),假设存在一个连续函数V(x)和参数λ1>0,λ2>0,0 <γa<1,0 <η<∞满足:
那么状态量x会在有限时间tf=max{tf1,tf2}内收敛到范围Ω=min{Ω1,Ω2}内。其中:
式中:ϑ是一个常数并且满足0 <ϑ<1。
1. 2 图 论
假设一个由n个跟随者和m个领航者所形成的无人机编队,其成员之间的通信链接拓扑可以用拓扑图来表示。 其中顶点集是一个有限的非空集合,表示各个无人机。 边集表示无人机之间的通信,其中Ni表示顶点i的邻接集,与顶点i邻接表示可以收到顶点i传来的信息。拓扑图G的加权邻接矩阵可以表示为Wg=,如果,则wij>0,反之wij=0。顶点i的度定义为,图G的度矩阵定义为Dg=diag{deg(),i=1,2,…,n+m}。那么图G的拉普拉斯矩阵就可以定义为Lg=Dg-Wg。由于假设领航者之间没有通信,则其拉普拉斯矩阵可以表示为
引理 3[20]矩阵是正定的。此外,定义矩阵,那么矩阵Ag是非负定的并且Ag的每一行元素的和为1。
定义2[19]如果任意,并且满足,其中c∈[0,1],那么称集合是一个凸集合。集合的凸包络则定义为。
引理 4[20]合围控制的目的就是将跟随者控制到领航者所形成的凸包Co(pl)内。如果合围控制成功,则跟随者会收敛到pf(t)=的 位 置 附 近 ,其 中pl=表示所有领航者的位置向量;表示所有跟随者的位置向量。
从引理4中可以看出,跟随者i的最终期望位置一定在凸包Co(pl)内,并且与通信矩阵相关,满足,其中,满足。这为2.1节设计基于精确队形的通信拓扑算法提供了支持。
1. 3 带有作动器故障的无人机模型
本文考虑一个由n个跟随者和m个领航者所组成的无人机编队。无故障的跟随者运动学和动力学模型如下[29]:
式中:xi、yi和zi分别是第i架无人机在惯性系下的三轴位置;Vi、ϕi、γi和χi分别是第i架无人机的速度、滚转角、航迹俯仰角和航迹偏航角;Ti、Li和Di分别是第i架无人机在机体系下受到的推力、升力和阻力;mi是无人机的质量;g是重力加速度;和表示无人机受到的有界外部干扰。定义和,则跟随者模型可以写成向量形式:
并且
根据相关文献的研究,多数的作动器故障可以表示为
式中:ςi=diag{ςi1,ςi2,ςi3}表示故障系数;hi表示未知偏置故障;ui0表示受限输入信号,该信号会在之后定义。
1. 4 输入受限信号的平滑处理
图1 直观地展示了本文提出的光滑函数与传统双曲正切光滑函数[30]之间的差异。

图1 光滑函数曲线Fig. 1 Curves of smooth functions
注释1通过与传统双曲正切光滑函数的比较不难发现本文所提出的光滑函数有2 个主要优点[30]。首先,本文所提出的光滑函数可以处理上下限同符号或上下限为0 的非对称约束函数,这是传统双曲正切光滑函数所不能处理的。其次,本文所提出的光滑函数的拟合误差取决于参数,即误差精度可以随需求调整。而传统双曲正切光滑函数的拟合误差则取决于约束上下界绝对值的最大值,这影响了最终系统的控制精度。
通过中值定理可以得到一个常数δ0∈(0,1),使得
2 基于精确编队的有限时间合围控制器设计
2. 1 基于精确队形的通信拓扑设计算法
由于大多数合围控制的研究只要求跟随者收敛到领航者所形成的凸包内,却对跟随者的精确队形没有限制,因此本文设计了一个针对预设跟随者队形的合围控制通信拓扑设计算法,如算法1 所示。
通过引理4 可以看出,使用算法1 所设计的合围控制通信拓扑结构会在合围控制误差收敛到0 时,使跟随者收敛到领航者所形成的凸包络内并且形成期望的预设队形。
注释2需要注意的是由算法1所设计的通信拓扑并不是唯一的。具体来说,由于矩阵Ag和可以有不同的选择,因此算法1可以提供很多可行解。
注释3算法1中要求Dg1[i,i]只要满足条件,并没有其他特殊要求。但是为了进一步简化通信的结构,减少通信负担,建议将Dg1[i,i]选择为。在这种情况下中会有更多的0 元素,这也就意味着跟随者与领航者之间存在更少的通信链路。

算法 1 通信拓扑设计算法1. 基于合围控制的特性限制,期望的预设队形必须处于凸包络Co(pl)内。根据引理4 可知,第i 架无人机的最终期望位置满足pi1d=([Ag]i⊗I3) pl,因此根据凸图形内部点的表达方式,设计一个矩阵Ag 2. 当 i ≤n 3. 如果 ∑j=1,j ≠i n aij[Ag]j( j=1,2,…,m)中的非零列与[Ag]i中的非零列在同一列,其中aij 是非零参数,那么4. Wg1[i,j]=■■■■■■■■■0 i=j aij ∑j=1,j ≠i n aij i ≠j 5. 否则 (即如果无法通过)选择aij ≥0,使 ∑j=1,j ≠i n aij[Ag]j的非零列与[Ag]i相同,那么Wg1[i,j]=0 ( j=1,2,…,m)6. 结束如果7. 如果Wg1[i,j]=0 ( j=1,2,…,m),则Dg1[i,i]=1 8. 否则9. 选择一个正实数Dg1[i,i]使其满足Dg1[i,i]≥max■■■■■■■■■■■■■()∑j=1,j ≠i n Wg1[i,j][ ]Ag j[ p][ ]Ag i[ p]■■■■■■■■■■■■■式中:p=1,2,…,m; [Ag]i[ p]≠0 10. 结束如果11. 结束循环12. 求解 Wg2=-(Dg1-Wg1) Ag 13. 返回 Dg1、Wg1 和Wg2
2. 2 分布式有限时间合围控制器设计
本节设计了一种基于Nussbaum 函数的分布式自适应有限时间容错合围控制器,解决了带有输入受限、外部干扰和作动器故障的无人机合围控制问题,最终使跟随者收敛到领航者所形成的凸包络内并形成精确队形。定义误差系统为
式中:ei1∈R3和ei2∈R3分别是第i架跟随者的位置误差和速度误差;是第i架跟随者的期望位置,由于领航者的状态是连续且有界的,因此不妨假设是未知正常数;pi2d是虚拟速度指令,该指令会在之后内容中定义。为了便于分析有限时间收敛性,定义新的误差系统:
式中:si1和si2为新的位置和速度误差;gi1和γ为控制参数。控制器设计过程如步骤1 和步骤2 所示。
步骤1首先,根据反步法的架构,设计位置子系统的控制律和自适应律为
式中:pi2d是虚拟速度指令;ki1、εP、βi1和βi2是控制参数;是自适应变量,满足是自适应误差。
选取位置系统的李雅普诺夫函数为
对其进行求导可得
将虚拟速度指令pi2d代入式(27)可得
进一步,通过Young 不等式可以得到
步骤2其次,根据虚拟速度指令,设计基于Nussbaum 函数的速度子系统控制律和自适应律为
对其进行求导可得
2. 3 稳定性分析
定理1针对带有输入饱和、外界干扰和作动器故障的跟随者无人机模型(式(19)),在控制律(式(24)、式(30)~式(32))和自适应律(式(25)、式(33))的作用下,跟随者可以在有限时间内收敛到领航者所形成凸包络内并且形成预设的精确队形。
证明首先证明系统的有界性,选取李雅普诺夫函数:
对其进行求导可得
因此通过引理1,可以得到V和δi是有界的结论,进而得出中各个元素均是一致最终有界的。
其次,证明系统的有限时间收敛性。选取另一个李雅普诺夫函数为
对其求导可得
式中:
因此根据引理2 可知,如果参数满足ki1>1,ki2>1/2mi+1,gi1>0,gi2>0,则该系统的误差可在有限时间tf=max{tf1,tf2}内收敛到原点的邻域Ωf=min{Ωf1,Ωf2}内。其中tf1和tf2取值为
至此,定理1 证毕。
注释4从上述分析中可以发现,误差收敛区域Ωf的大小与υs2相关,而υs2的大小与光滑函数的最大拟合误差有关。传统双曲正切函数的最大拟合误差取决于,这使得当上下界较大时,误差的收敛域Ωf也会变大,影响控制效果[28]。而本文提出的光滑曲线可以通过选择参数εu使最大拟合误差可调,从而缩小误差的收敛域,提高控制精度。
3 数字仿真
本节展示了一些数字仿真结果,验证了本文所提出的算法和控制律的有效性。仿真基于由3 架跟随者和4 架虚拟领航者组成的无人机编队,其初始位置信息如表1 所示。从中不难看出,领航者初始位置的选择与其速度均保持一致,在仿真时间内虚拟领航者一直保持为处于XOZ平面内的长方形队形。设计跟随者的预设队形为一个在XOZ平面内的三角形,并且处于领航者所形成的凸包络内部。其中,虚拟领航者的速度被设置为vl=[30,0,5sin(0.1t)]Tm/s;无人机的质量被设置为5 kg;外界的干扰信号被设置为。根据工程经验,将无人机的输入信号上下界限制设为,和。此外,表2给出了控制器的参数。表3 给出了跟随者故障产生的时间和类型。

表1 无人机编队初始状态Table 1 Initial states of UAV team

表2 控制参数Table 2 Parameters of controller

表3 跟随者故障信息Table 3 Information of faults for followers
根据预设队形和算法1,该队形可以用矩阵Ag表示为
从注释2 中可知,通过选择不同的Dg1可以得到不同的通信拓扑图。例如分别选择diag{2,2,1}和=diag{2,4,1},得到的通信拓扑如图2 和图3 所示。

图2 基于 的通信拓扑图Fig. 2 Communication topology graph based on
从图中标红的通信连线不难看出,当选择时,编队中的通信结构会更加简单,跟随者和领航者的通信链路会更少。因此,注释2 中的内容得到了证实。
由表3 可知,在仿真过程中第1 架无人机在第20 s 发生故障,第2 架无人机在第30 s 发生故障,第3 架无人机在第10 s 发生故障。图4~图10展示了本文所提出的基于Nussbaum 函数的有限时间自适应合围容错控制器的数字仿真结果。

图4 无人机编队轨迹Fig. 4 Trajectories of UAV team
图4 给出了无人机编队的航迹图,从中可以看出跟随者在故障的情况下,最终形成了预设的三角队形并且收敛到了领航者所形成的凸包络内。图4 证实本文所提出的通信拓扑设计算法和有限时间容错控制器的有效性。为了更直观地观察控制效果,图5 和图6 给出了系统误差的仿真图。可以看到无人机的跟踪误差都在2.9 s 左右收敛到了原点附近。此外,在20、30 和10 s 故障发生的时候,误差由于系统故障的原因暂时增大,并很快又重新收敛,这验证了本文所提出的控制器的容错性和鲁棒性。图7 和图8 给出了自适应信号的曲线图,验证了其有界性。此外,图9 展示了Nussbaum 信号。在故障发生后,该信号会显著增加进而补偿因故障所损失的控制量。图10 展示了无人机的控制输入信号。从图10 中可以看出输入信号均处在限制的范围内。由此验证了本文提出的控制器在输入受限情况下的控制效果。

图5 无人机编队位置误差Fig. 5 Position errors of UAV team

图6 无人机编队速度误差Fig. 6 Velocity errors of UAV team

图7 自适应信号D̂iFig. 7 Adaptive signal D̂i

图8 自适应信号P̂iFig. 8 Adaptive signal P̂i

图9 Nussbaum 信号ξiFig. 9 Nussbaum signal ξi

图10 无人机编队控制输入Fig. 10 Control input signals of UAV team
为了比较本文所提出的容错方法与其他容错方法的优劣,选择了自适应容错方法(Adaptive Fault Tolerant Control, AFTC)[31]和基于RBFNN 观测器的容错方法(Adaptive RBFNN Observer-based Fault Tolerant Control,AROFTC)[19]与本文控制器进行仿真。AFTC的控制效果如图11~图13 所示。从仿真图中不难看出,由于AFTC 的收敛效果和故障系数显性相关,因此仅依靠自适应算法会导致其误差收敛时间较长,控制效果较差。具体来说,对比图11和图4 可看出基于AFTC 的无人机航迹有明显被作动器故障影响的痕迹。对比图12 和图13 与图5 和图6 可以看出,基于AFTC 的仿真结果中由作动器故障引起的误差波动也有明显增加。

图11 AFTC 无人机编队轨迹图Fig. 11 Trajectories of UAV team with AFTC

图12 AFTC 无人机编队位置误差Fig. 12 Position errors of UAV team with AFTC

图13 AFTC 无人机编队速度误差Fig. 13 Velocity errors of UAV team with AFTC
此外,由于RBFNN 具有出色的拟合特性,因此选择了一种基于RBFNN 观测器的容错控制器作为AROFTC 的代表与本文容错控制器进行比较。从图14~图16 中不难看出,在AROFTC 控制器下作动器故障引起的误差波动小于本文所提出的控制器,因此基于RBFNN 观测器的容错控制方法的效果优于本文所提出的控制器。由图17 可见,观测器对故障和误差的估计是比较准确的,这为控制器设计提供了良好的参考信号。但是,基于观测器的容错控制方法需要对观测器进行设计,这增加了控制器的设计难度和复杂度。因此,在综合考虑控制器复杂度和控制效果的情况下,所提出的控制器为容错控制提供了一个折中的选择。

图14 AROFTC 无人机编队轨迹Fig. 14 Trajectories of UAV team with AROFTC

图15 AROFTC 无人机编队位置误差Fig. 15 Position errors of UAV team with AROFTC

图16 AROFTC 无人机编队速度误差Fig. 16 Velocity errors of UAV team with AROFTC
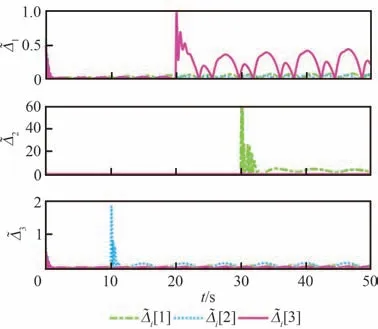
图17 RBFNN 网络的拟合误差Fig. 17 Fitting errors of RBFNN
为了验证所提出的基于Nussbaum 函数的控制方法(Nussbaum-based Control, NC)的效果,仿真选择了升阶Nussbaum 饱和控制方法[28](Increasing Order Nussbaum-based Control,IONC)与本文的控制器进行对比。为了更好地展示针对输入饱和问题的控制效果,仿真对象设置为无干扰和故障跟随者1 无人机。
仿真结果如图18~图20 所示。从图19 和图20 可以看出本文所设计的控制器收敛时间更快,控制效果更好。这是因为本文没有将控制输入信号看作一阶系统,即对输入信号进行升阶处理。因此,避免了控制输入初始值的设计不合理以及输入信号的变化率受到一阶积分系统限制等问题。相比之下,本文设计的控制器具有设计简单、控制效果好等优点。图21 展示了Nussbaum 函数中自变量的变化曲线。

图18 跟随者1 控制输入Fig. 18 Control input signals of Follower 1 with different methods
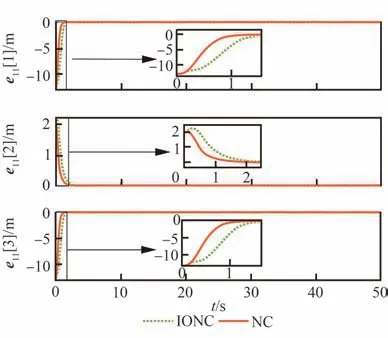
图19 跟随者1 位置误差Fig. 19 Position errors of Follower 1 with different methods

图20 跟随者1 速度误差Fig. 20 Velocity errors of Follower 1 with different methods
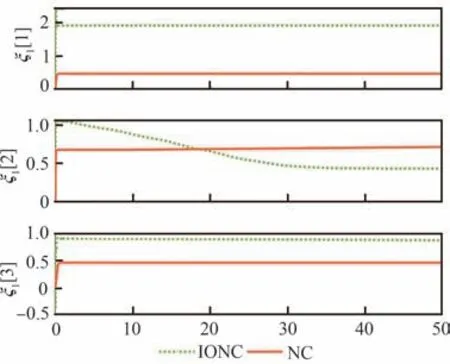
图21 Nussbaum 信号ξ1Fig. 21 Nussbaum signal ξ1
4 结 论
本文对带有输入饱和、作动器故障和外界干扰的无人机精确编队合围容错控制展开了研究,具体结论如下所示:
1) 针对在合围控制框架下跟随者形成精确预设队形的问题,提出了一种基于预设队形的通信拓扑设计方法,可以使跟随者最终在领航者所形成的凸包络内形成精确队形。
2) 针对输入饱和问题,提出了一种新颖的双曲正切函数对上下界同号或为0 的非对称饱和函数进行平滑处理,将存在输入饱和及作动器故障情况下的无人机合围控制问题转化为变增益控制问题。
3) 针对输入饱和、作动器故障问题,提出了一种基于Nussbaum 函数的分布式自适应有限时间合围控制器,使误差在有限时间收敛到原点的一个任意小的邻域内,并最终通过李雅普诺夫稳定性完成了闭环系统稳定性的证明。
