基于对称与反对称谷边缘态的声能谷输运

施斌杰,贾鼎,葛勇

（江苏大学物理与电子工程学院，镇江，212013）

近年来，拓扑绝缘体在凝聚态物理领域受到研究学者们的广泛关注，已成为当前研究热点方向之一，此概念也被引入到经典波领域［1-4］.例如，在声学领域［5-8］，研究人员通过设计各类具有拓扑保护的声学人工结构，可以实现对声传输的高鲁棒性操控及多种声拓扑绝缘体，如类量子霍尔声拓扑绝缘体［9-10］、类量子自旋霍尔声拓扑绝缘体［11-12］、Floquet 声拓扑绝缘体［13-15］、谷霍尔声拓扑绝缘体［16-21］、高阶声拓扑绝缘体［22-23］等.

在上述拓扑绝缘体中，具有能谷自由度的谷霍尔声拓扑绝缘体，因其丰富的谷拓扑物理内涵及其潜在的应用前景而备受关注.在此方面，通过打破声子晶体的镜像或空间反演对称性，可以实现谷霍尔声拓扑绝缘体.如通过旋转三角晶格声子晶体［16-18］单元，打破晶格的镜像对称性，可以实现声能谷输运；通过调节Kagome 晶格声子晶体单元［19-20］的结构参数，打破其空间反演对称性，实现谷拓扑绝缘体；此外，基于二聚体谐振腔的正方晶格声子晶体［21］，调节单元的结构参数，可以实现声学谷拓扑绝缘体.上述工作均很好地展示了谷拓扑绝缘体的优点及特性.然而，基于谷边缘态对称分布特征［16］的声能谷输运研究尚未开展.

本工作基于蜂窝型声子晶体设计实现了包含两种不同界面（Ⅰ和Ⅱ）的谷拓扑波导.声子晶体单元由两种镂空散射体组成.通过调节镂空散射体中通道宽度，可以实现声子晶体的能带反转.基于两种不同谷霍尔相的声子晶体，设计实现包含界面Ⅰ和Ⅱ的两种谷拓扑波导.研究发现，界面Ⅰ和Ⅱ中的谷边缘态分别具有反对称和对称分布特征.数值模拟反相与同相声源激发包含界面Ⅰ与Ⅱ的谷拓扑波导的谷边缘态及其声能谷输运特征.在此基础上，在界面Ⅰ和Ⅱ中引入Z 型和V型缺陷，进一步验证了谷拓扑波导中声能谷输运的鲁棒性.最后，在所设计的谷拓扑波导两侧分别放置一对声源，通过主动控制声源初始相位，设计实现了可调控声非对称传输效应.

1 数值模拟与讨论

1.1 声子晶体结构与性能图1a 显示所设计的基于镂空散射体的二维蜂窝结构声子晶体.声子晶体晶格常数a=mm，单元（平行四边形区域）由两种镂空散射体（半径r=9 mm）组成，相邻散射体间距d=20 mm，散射体中三条空气通道的夹角θ=120°，左右两侧散射体的通道宽度分别为w1和w2.本文采用COMSOL Multiphysics软件数值模拟声子晶体中的声传输，在数值模型中，散射体边界设置为硬声场，空气密度ρ=1.21 kg·m-3，声速c=343 m·s-1.图1b 显示数值模拟两种不同参数声子晶体的色散关系，其中Δw=w1-w2，且保持w1+w2=10 mm.可以看出，当时（实线），在K 点形成狄拉克锥；而当=0.2 时（虚线），声子晶体的蜂窝晶格空间反演对称性被破坏，进而K 点的二重简并被打破，在13.8～14.4 kHz 区间形成直接带隙.

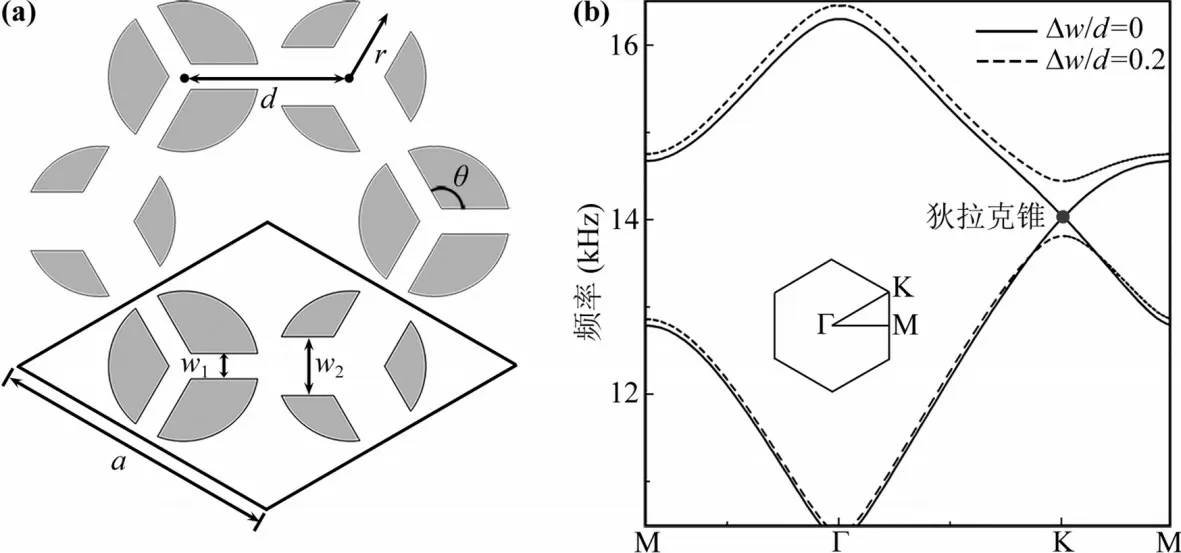
图1 声子晶体结构(a)及其色散关系(b)，插图为第一布里渊区Fig.1 (a) Structure and (b) dispersion relations of sonic crystals，and the inset in (b) is the 1st Brillouin zone

图2a 显示带隙底部与顶部的本征态频率与参数Δ之间的关系（其他参数不变），其中，K1，K2，K3和K4点分别为Δ=±0.2 对应的带隙底部与顶部的本征态.可以看出，当参数Δ从负值逐渐增大时，带隙宽度逐渐变小，带隙顶部与底部的本征态在Δ=0 处发生简并；当Δ变为正值时，简并被打开，带隙宽度逐渐增大.图2b 显示本征态K1，K2，K3和K4对应的声压场分布.可以看出，本征态K1和K4的场分布相同，声涡旋沿着逆时针方向，本征态K2与K3的场分布相同，声涡旋沿着顺时针方向，表现出典型的能带反转特征，从而说明Δ=±0.2 对应的两种声子晶体产生了谷霍尔相变.基于两种不同谷拓扑相的声子晶体，可以设计包含两种不同界面的谷拓扑波导.

图2 (a)带隙底部与顶部本征态的频率与参数Δwd 关系,本征态K1,K2,K3,K4分别对应参数△w/d=±0.2；(b)数值模拟的本征态K1,K2,K3,K4对应的声压场分布，箭头表示声能流方向，环形箭头为声涡旋方向Fig.2 (a) Eigenfrequencies of the band edge states as a function of Δwd,the edge states K1，K2，K3 and K4 correspond to the parameters △w/d=±0.2,(b) simulated pressure distributions of the edge states K1，K2，K3 and K4,the arrows represent the direction of energy flux，and the circular arrows are the direction of sound vortex

1.2 超原胞色散关系与谷边缘态特性图3a 显示基于声子晶体A（Δ=-0.2）与B（Δ=0.2）构建的两种不同界面（Ⅰ与Ⅱ）的谷拓扑波导超原胞.超原胞色散关系如图3b.可以看出，对于含界面Ⅰ的超原胞，其带隙存在一对群速度相同、方向相反的谷边缘态（实线），其中和分别为谷K 和Kʹ的投影，群速度分别为正和负；对于含界面Ⅱ的超原胞，同样存在着一对谷边缘态和（虚线），其色散关系特征与界面Ⅰ相反.为了进一步显示上述谷边缘态特征，数值模拟图3b中M，N，P 和Q 点对应的谷边缘态声压场分布，如图3c.可以看出，在包含界面Ⅰ的超原胞中，M与N 模式的场分布相同，关于界面Ⅰ反对称；在包含界面Ⅱ的超原胞中，P 与Q 模式的场分布相同，关于界面Ⅱ对称.上述具有反对称和对称模式场分布的两种谷边缘态，可以实现声能谷输运及其相关的新效应.

图3 两种谷拓扑波导超原胞结构(a)及其色散关系(b),(c)谷边缘态M,N,P 和Q 的声压场模式分布(虚线表示界面Ⅰ和Ⅱ)Fig.3 (a) Structures of the supercells of both valley topological waveguides，and (b) their corresponding dispersion relations,(c) pressure distributions of the valley edge states M，N，P and Q (The dashed lines are the domain walls Ⅰ and Ⅱ)

2 声能谷输运与鲁棒性验证

2.1 声能谷输运基于谷边缘态的反对称与对称模式分布特征，数值模拟包含界面Ⅰ和Ⅱ的谷拓扑波导声能谷输运，其中模型四周边界均设置为平面波辐射条件.如图4a，在包含界面Ⅰ的谷拓扑波导的左侧放置一对反相声源，可以看到，反相声源在界面Ⅰ中激发产生谷边缘态，声能量可以沿着界面Ⅰ进行高效地传输.然而，将声源相位设置为同相（图4b），拓扑波导中的谷边缘态无法被激发，界面Ⅰ中的声能量几乎为0，声波无法传输.这主要是因为谷边缘态的激发与声源相位分布密切相关，当声源相位分布与谷边缘态的场分布相同时，可以在界面中激发产生谷边缘态，反之则无法激发.为了进一步验证该结论，采用一对反相声源激发包含界面Ⅱ的谷拓扑波导（图4c），可以看出，与界面Ⅰ相反，界面Ⅱ中的谷边缘态无法被激发.而将声源相位设置为同相，具有对称分布特征的谷边缘态可以被有效激发，声能量能够通过包含界面Ⅱ的波导（图4d）.上述结果表明，基于两种不同界面谷拓扑波导中的反对称与对称模式的谷边缘态，通过改变声源的相位，可以对声能谷输运进行有效调控.

图4 (a)反相与(b)同相声源激发包含界面Ⅰ的谷拓扑波导产生的声能量分布；(c)反相与(d)同相声源激发包含界面Ⅱ的谷拓扑波导产生的声能量分布（声源频率为14.0 kHz，一对黑色与白色五角星表示反相声源，一对黑色五角星表示同相声源）Fig.4 Acoustic intensity distributions in the valley topological waveguide with the domain wall Ⅰ under the excitation of a pair of (a) out⁃phase and (b) in⁃phase sources，and those with the domain wall Ⅱ under the excitation of a pair of (c) out⁃phase and (d) in⁃phase sources（The excitation frequency is 14.0 kHz，and the dashed lines indicate the domain walls，and a pair of black and white stars present a pair of out⁃phase sources，and a pair of black stars are a pair of in⁃phase sources）

为了显示声能谷输运的带宽，数值模拟反相和同相声源分别激发两种谷拓扑波导产生的声透射谱.如图5a，在体带隙中（阴影区域），反相声源激发对应的声透射率均在-5 dB 之上，从而说明界面Ⅰ中谷边缘态被有效激发.而同相声源激发对应的声透射率均在-30 dB 之下，声能量无法在界面Ⅰ中传输.对包含界面Ⅱ的谷拓扑波导，如图5b，采用反相和同相声源激发产生的透射谱特征与图5a 中正好相反.基于上述结果可以得到，基于反对称和对称模式谷边缘态的声能谷输运，可以在声子晶体的体带隙范围实现.

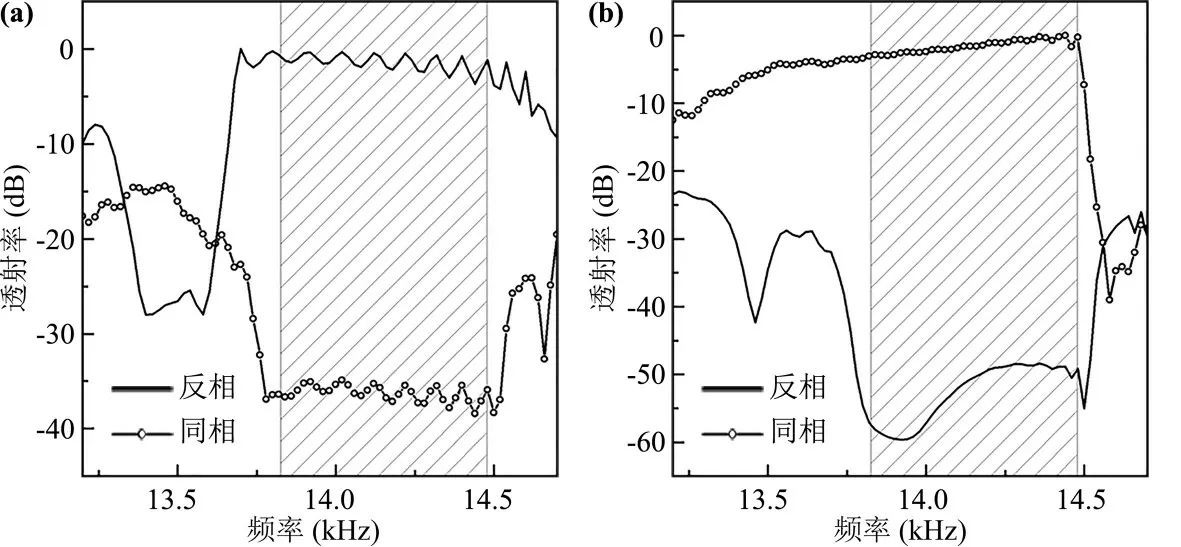
图5 反相与同相声源分别激发包含(a)界面Ⅰ与(b)Ⅱ的谷拓扑波导产生的声透射谱,阴影区域表示体带隙(13.8～14.4 kHz)Fig.5 Transmittance spectra of the topological waveguides with the domain walls (a) Ⅰ and (b) Ⅱ under the excitations of a pair of out⁃phase and in⁃phase sources，respectively,shaded regions are the bulk bandgap (from 13.8 to 14.4 kHz)

2.2 鲁棒性验证在两种谷拓扑波导的界面中引入缺陷，数值模拟声能谷输运的鲁棒性.如图6a，在谷拓扑波导界面Ⅰ中引入Z 型缺陷，采用反相声源激发产生的声能量可以有效通过Z 型缺陷，沿界面Ⅰ传输.图6b 显示数值模拟反相声源激发包含Z 型缺陷的界面Ⅰ产生的声透射谱（实线），作为对比，引入无缺陷界面Ⅰ对应的声透射谱（实线+空心圆点）.可以看出，在阴影区域对应的体带隙中，两种情况对应的声透射谱几乎相同，说明所产生的声能谷输运几乎无背向散射，对Z 型缺陷具有较好的免疫性.图6c 和6d 显示在谷拓扑波导界面Ⅱ中引入Z 型缺陷的模拟结果，可以看出，所对应的声能谷输运鲁棒性与界面Ⅰ相同.在此基础上，在两种谷拓扑波导界面引入V型缺陷，数值模拟结果见图7，可以看出，两种谷拓扑波导中产生的声能谷输运同样对V 型缺陷具有很好的免疫性.综上，基于反对称和对称模式谷边缘态的声能谷输运具有很好的鲁棒性.

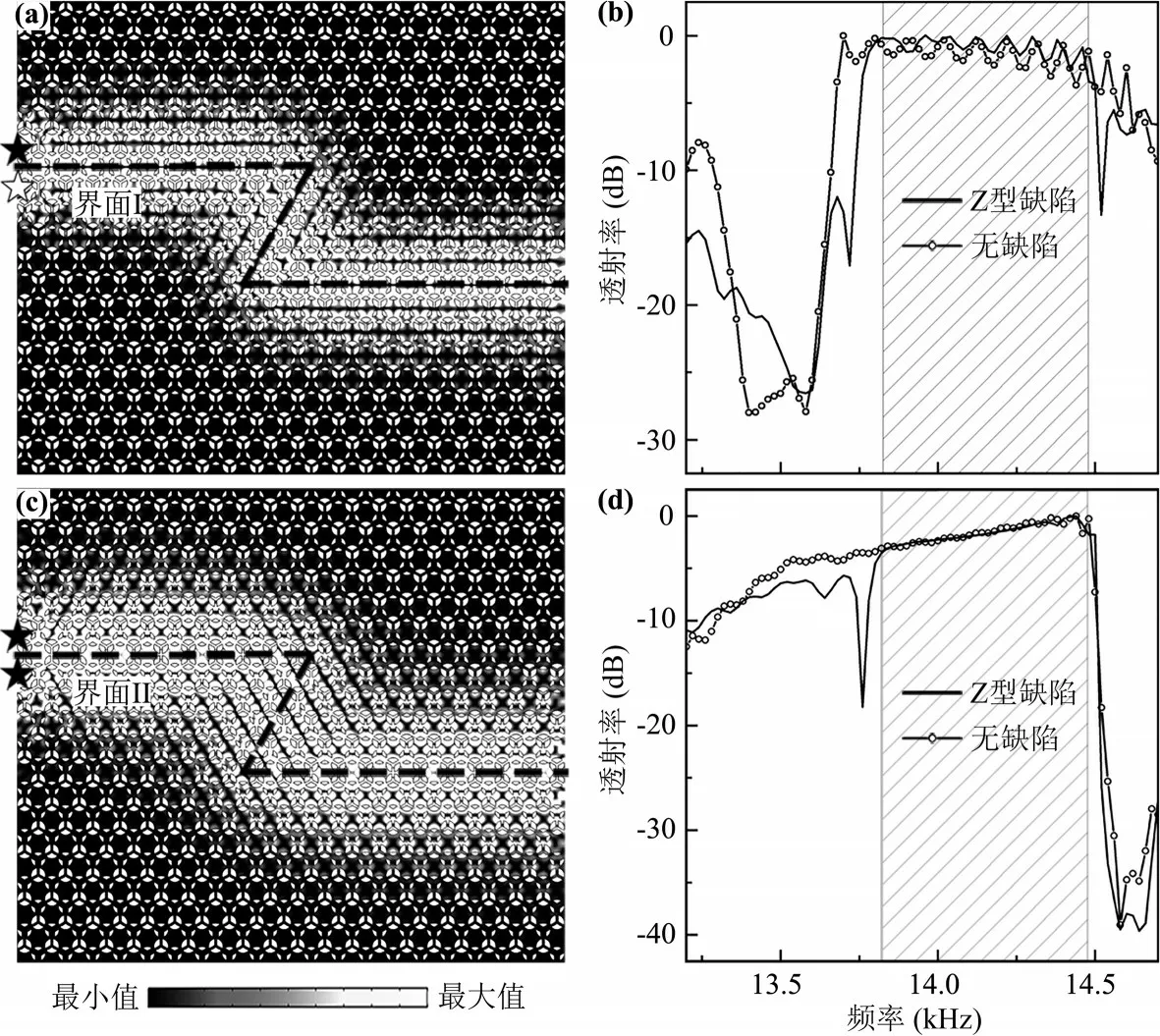
图6 (a)频率为14.0 kHz 的反相声源激发包含Z 型缺陷的界面Ⅰ产生的声能量分布;(b)反相声源激发包含Z 型缺陷与无缺陷的界面Ⅰ产生的声透射谱;(c)频率为14.0 kHz 的同相声源激发包含Z 型缺陷的界面Ⅱ产生的声能量分布;(d)同相声源激发包含Z 型缺陷与无缺陷的界面Ⅱ产生的声透射谱((b)和(d)中阴影区域为体带隙(13.8～14.4 kHz))Fig.6 (a) Acoustic intensity distribution in the domain wall Ⅰ with a Z⁃shaped defect under the excitation of a pair of out⁃phase sources at 14.0 kHz，and (b) transmittance spectra through the domain wall Ⅰ with and without Z⁃shaped defect;(c) acoustic intensity distribution in the domain wall Ⅱ with a Z⁃shaped defect under the excitation of a pair of in⁃phase sources at 14.0 kHz，and (d) transmittance spectra through the domain wall Ⅱ with and without Z⁃shaped defect (shaded regions in (b) and (d) are the bulk bandgap (from 13.8 to 14.4 kHz))

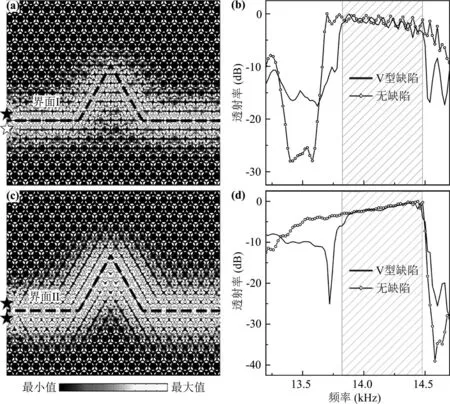
图7 (a)频率为14.0 kHz 的反相声源激发包含V 型缺陷的界面Ⅰ产生的声能量分布;(b)反相声源激发包含V 型缺陷与无缺陷的界面Ⅰ产生的声透射谱;(c)频率为14.0 kHz 的同相声源激发包含V 型缺陷的界面Ⅱ产生的声能量分布;(d)同相声源激发包含V 型缺陷与无缺陷的界面Ⅱ产生的声透射谱Fig.7 (a) Acoustic intensity distribution in the domain wall Ⅰ with a V⁃shaped defect under the excitation of a pair of out⁃phase sources at 14.0 kHz，and (b) transmittance spectra through the domain wall Ⅰ with and without V⁃shaped defect，(c) acoustic intensity distribution in the domain wall Ⅱ with a V⁃shaped defect under the excitation of a pair of in⁃phase sources at 14.0 kHz，and (d) transmittance spectra through the domain wall Ⅱ with and without V⁃shaped defect

3 应用探索

最后，基于包含界面Ⅰ的谷拓扑波导提出一种方向可调控的声非对称传输器件的设计方案.如图8a，在谷拓扑波导界面Ⅰ左右两侧分别放置一对声源，将其相位分别设置为反相和同相状态，可以看出，左侧反相声源可以激发反对称分布的谷边缘态，到达拓扑波导右侧；右侧同相声源不能激发谷边缘态，声能量无法通过拓扑波导.数值模拟的左侧反相和右侧同相声源激发谷拓扑波导产生的声能量分布分别如图8b 和图8c.可以看出，左侧反相声源激发产生的声能量能通过拓扑波导，而右侧同相声源激发的声波无法在拓扑波导中传输，从而实现声波非对称传输效应.在此基础上，将两侧声源的初始相位分别调整为同相和反相（图8d），则声非对称传输方向发生反转，数值模拟的声能量分布如图8e 和图8f，表现出明显的反转声非对称传输效应.基于上述结果可以得到，通过主动控制界面两侧声源的初始相位，可以实现方向可调控的声非对称传输效应.

图8 (a)基于包含界面Ⅰ的谷拓扑波导设计的声非对称传输器件示意图;(b)频率为14.0 kHz 的左侧反相与(c)右侧同相的声源激发包含界面Ⅰ的谷拓扑波导产生的声能量分布;(d)声非对称传输方向反转示意图;(e)频率为14.0 kHz 的左侧同相与(f)右侧反相的声源激发包含界面Ⅰ的谷拓扑波导产生的声能量分布Fig.8 (a) Schematic of an acoustic asymmetric transmission device based on the valley topological waveguide with the domain wall Ⅰ,acoustic intensity distributions in valley topological waveguides with the domain wall Ⅰ under the excitations of a pair of (b) out⁃phase and (c) in⁃phase sources at the left and right sides，respectively,(d) schematic of the revseal of acoustic asymmetric transmission by adjusting the initial phases of sound sources on both sides,acoustic intensity distributions in valley topological waveguides with the domain wall Ⅰ under the excitations of a pair of(e) in⁃phase and (f) out⁃phase sources at the left and right sides，respectively

4 结论

本文研究基于对称与反对称谷边缘态的声能谷输运效应.基于蜂窝型声子晶体提出了包含界面Ⅰ和Ⅱ的两种谷拓扑波导，其中声子晶体单元由两种镂空散射体组成.通过调节散射体的空气通道宽度，可以实现声子晶体的能带反转.基于两种不同谷霍尔相的声子晶体，设计实现了包含界面Ⅰ和Ⅱ的谷拓扑波导.数值结果表明，在包含界面Ⅰ和Ⅱ的谷拓扑波导体带隙中分别存在着一对群速度相同、传播方向相反的谷边缘态，其对应的模式场分布分别具有反对称和对称特征.在此基础上，采用一对反相与同相声源分别在界面Ⅰ与Ⅱ上激发产生反对称与对称分布的谷边缘态，并可以在体带隙中实现声能谷输运.而采用同相与反相声源无法在界面Ⅰ与Ⅱ上激发产生谷边缘态.此外，在谷拓扑波导界面Ⅰ和Ⅱ中分别引入Z 型和V 型缺陷，模拟反相与同相声源激发两种谷拓扑波导产生的声能量分布及其声透射谱.通过比较分析，所设计的两种谷拓扑波导均具有很好的鲁棒性.最后，探索了所设计的谷拓扑波导潜在应用方案，通过主动控制波导两侧声源的初始相位，实现了可调控声非对称传输效应.本文为研究声子晶体中能谷输运提供了新思路，并在设计高鲁棒性可调控拓扑声学器件方面具有潜在的应用价值.