基于CEL 的管道清管器90°弯头通过性能分析*

戴朝磊 刘畅 张庆保 陈金忠 付双成 吴胜平

(1. 常州大学机械与轨道交通学院 2. 中国特种设备检测研究院3. 江苏省特种设备安全监督检验研究院 4. 国家压力管道元件质量检验检测中心)

0 引 言

长距离油气输送管道工况复杂, 使用过程中易产生裂纹、 腐蚀等损伤。 为延长使用寿命并提高安全性, 常采用清管器对管道内的积液和结蜡等杂物进行清除。 清管器皮碗采用聚氨酯材料, 运动状态复杂, 通过弯管工况时, 皮碗受挤压变形严重, 清管器姿态变化剧烈。 皮碗与管壁之间的密封状态受到破坏, 发生泄流导致速度减慢甚至卡堵, 诱发凝管事故。 清管器在大管径管道应用成熟, 但小管径管道工况存在动力不足及通过性困难的问题亟待解决。

相关研究包括, 赵海旭等[1]通过尺寸分析了清管器过弯性能, 但未考虑清管器自身结构因素。李娜[2]建立了输气管道在线内检测器的受力简化模型和运动方程, 得到结构、 表面粗糙度及管内障碍物等对在线内检测器稳定运行所需驱动压差的影响。 ZHANG H. 等[3]计算并分析了用于DN200 管道直板清管器的密封皮碗过盈量、 夹持皮碗半径及厚度对密封皮碗接触应力、 弯曲应力及弯曲角度的影响。 刘小明[4]对心轴式清管器进行了动力学分析, 得到了皮碗在不同压差、 不同管径以及通过焊缝余高时相关性能的值以及其变化规律。 吴旭等[5]构建了皮碗在管道中的受力模型, 研究了碟形皮碗不同唇部弯曲角度对接触应力的影响。 陈浩等[6]分析了3 种皮碗结构的受力, 得到了皮碗在不同唇长和工作压差时皮碗性能的变化规律。 上述研究基于二维模型分析了清管器性能受结构的影响情况, 但未考虑聚氨酯皮碗相邻两截面之间的拉应力。 魏云港等[7-9]研究了相关结构参数对皮碗动力学特性的影响, 基于三维准静态模型对清管器过弯通过性进行分析, 未考虑流体介质与清管器之间的作用, 忽略了静水压力的影响, 摩擦力与实际工程情况有差别。 孙其海[10]研究了双节式清管器通过不同焊点时动力学响应性能。 江旭东等[11]对比分析了不同管道内径和机器人舱段长度下的密封皮碗应力场、 管道与机器人间的摩擦力和流体对管道机器人的驱动压差。 任宏喜[12]探究了不同工作环境下双节检测器的受力情况, 得出双舱段检测器在直管和弯管内顺利通过的关键尺寸约束范围。 上述研究着重于清管器皮碗受力与变形情况, 未深入分析清管器动力学响应性能。

现有相关研究主要聚焦清管器过弯受力情况及整体尺寸分析, 鲜有关于清管器结构参数对过弯能力影响的分析。 笔者以直径168 mm 管道清管器为对象, 提出了以动力学响应特性和变形状态为依据的通过性评价方法, 研究过盈量、 夹持率及皮碗结构形式对清管器90°弯头通过能力的影响, 以期为清管器优化设计及工程应用提供理论指导。

1 三维准静态与流固耦合模型对比

1.1 三维准静态模型

清管器过弯过程示意图如图1 所示, 该模型由发球筒、 直管及弯管组成。 模型相关参数如表1所示。

图1 清管器过弯几何模型示意图Fig.1 The geometry model of a pig passing through an elbow

清管器由碟形皮碗、 夹持钢板及心轴组成, 夹持钢板将皮碗通过夹紧螺栓固定在心轴上。 管道及心轴采用45 号钢材料, 密度为7.85 g/cm3, 弹性模量为201 GPa, 泊松比为0.3。 清管器皮碗选用聚氨酯材料, 根据Mooney-Rivlin 模型[13], 定义其密度为1.2 g/cm3, 材料正定常数C10为1.42 MPa、C01为0.36 MPa, 管道及心轴设置为刚体。 夹持钢板与皮碗设置绑定约束。 清管器模型及网格示意图如图2 所示。 将管道内壁设置为主面, 清管器4 个皮碗设置为从面, 将该组面设置为面面接触以模拟皮碗进入过盈管道后受流体介质推动在管道中运动。 切向力学行为定义为罚接触, 摩擦因数定义为0.4, 法向力学行为设置为“硬” 接触, 对管道施加固定约束。 过弯分为3 个阶段, 第一阶段为水平直管段, 清管器由发球筒进入水平直管段; 第二阶段为弯管段; 第三阶段为竖直直管段, 清管器出弯后在竖直管段内运行, 对清管器施加沿管道轴线的位移约束以模拟过弯过程。 该模型采用六面体网格进行划分, 网格类型为C3D8H。

图2 清管器模型及网格示意图Fig.2 Pig model and meshing

1.2 流固耦合模型

本节采用基于CEL 方法的流-固耦合模型对清管器过弯过程的动力学响应进行分析。 通过在清管器尾部施加流体介质推动其运动, 模拟过弯行为。拉格朗日网格随物体变形而变化, 材料产生大变形时网格发生较大畸变导致计算无法收敛, 故该算法仅适用于小变形模型。 欧拉算法将网格固定, 材料可以在欧拉网格域内自由流动, 但物体之间的界面无法通过欧拉算法得出。 耦合拉格朗日-欧拉算法(CEL) 结合了2 种算法的优点。 在CEL 算法中,采用拉氏体积分数(Eulerian Volume Fraction) 更新材料在欧拉网格中的状态和位置[14]。EVF定义为欧拉材料在空间中的体积比,EVF范围为0 ～1,EVF=1 时, 材料充满网格;EVF=0 时, 网格内无材料; 网格内含有部分材料时, 则按照材料所充满欧拉网格的比例来计算EVF的值。 流固耦合的边界通过EVF和拉格朗日区域方向通过重构而确定, 重构过程如图3 所示。 拉格朗日域与欧拉域之间的接触通过基于罚函数算法的通用接触分析获得[15]。

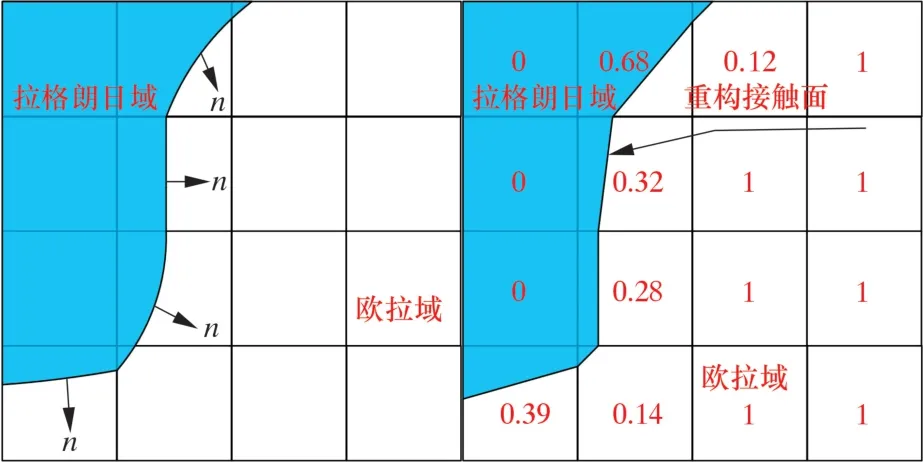
图3 接触面重构过程Fig.3 Contact surface reconstruction process

本文采用EOS 方法线性Us-Up Hugoniot 形式的Mie-Grineisen 状态方程描述流体介质的状态。其假设压力p为密度ρ的函数, 其能量方程可通过连续性方程和动量方程求解。

在CEL 方法中连续方程和动力方程为[16]:

式中:ρ为流体密度, kg/m3;d为流体流道直径,m;t为流体流过时间, s;g为重力加速度, m/s2;σ为流体接触应力, Pa。

为保证管道内检测器良好的检测效果, 油气管道投产前常采用清管器对管道内杂质及结蜡进行清理。 该工况采用水介质对清管器进行驱动, 具体参数如表2 所示。

表2 流体介质材料参数Table 2 Material parameters of fluids

流固耦合有限元模型如图4 所示。 清管器与管道采用Lagrangian 网格进行划分, 流体域采用Eulerian 网格进行划分。 流体域包含管道, 故流体域尺寸大于管道内清管器运动的区域。 初始流体域定义了流体域内初始流体的区域, 该处EVF=1, 流体域内其他网格EVF均为0。 清管器及管道的网格单元属性为C3D8R, 流体域的网格单元属性为EC3D8R。 将发球筒的入口设置为流体域的速度入口, 速度为1 m/s, 自由度不加限制。 竖直直管段下端为流体域的出口, 出口类型设置为零压面以防止流体倒流; 对管道设置位移全约束以防止发生刚体位移。 对模型施加通用接触设置, 接触类型为罚函数接触。

图4 清管器运行通过弯管的流固耦合模型初始流体域Fig.4 Initial fluid domain of the FSI model of the pig passing through the elbow

1.3 结果分析

如图5 所示, 三维准静态模型清管器运行初期摩擦力骤增至1 480 N。 水平直管段内摩擦力保持为275 N 左右, 进入弯管后摩擦力骤增至803 N 后缓慢下降, 过弯60%后摩擦力再次升高至585 N。

图5 流固耦合与三维准静态模型过弯摩擦力变化情况Fig.5 Elbow-passing friction changes of FSI model and 3D quasi-static model

分析原因, 清管器姿态发生变化, 接触面积增大。 清管器出弯后进入竖直管道, 摩擦力降至275 N, 与水平管道清管器所受摩擦力相同。 流固耦合过弯过程摩擦力变化情况与准静态相比有较大差别, 工况初期清管器受到流体介质冲击后摩擦力剧烈增加, 达到3 200 N; 4 个皮碗依次进入过盈管道, 摩擦力出现4 次爬升。 如图5d 所示, 4 次爬升的间隔逐渐增加, 依次为0.02、 0.03、 0.05 和0.09 s。 4 个皮碗进入管道后摩擦力减小, 水平直管段摩擦力稳定在1 077 N。 进入弯管后摩擦力急剧增加至1 953.677 N 后逐渐降低, 整体趋势与三维准静态模型类似, 但波动较大。 出弯后清管器进入竖直管段, 受重力作用摩擦力较水平管段略有提升, 提升至1 162.273 N。 流固耦合模型中清管器受静水压力作用, 摩擦力远大于三维准静态模型且贴合实际, 故下文选用三维流固耦合模型对清管器过弯性能进行分析。

2 基于CEL 的清管器弯管通过性能分析

2.1 清管器弯管通过性能评价指标

本节以3%过盈量清管器过弯示意图为例, 研究清管器过弯受力变形情况, 结果如图6 所示。 过弯时心轴运行姿态偏转, 皮碗环向变形呈不对称分布。 第2、 4 皮碗受管壁挤压变形严重, Mises 应力集中在第2 个皮碗的小曲率弯管侧(内侧) 和第4个皮碗的大曲率弯管侧(外侧), 最大Mises 应力为1.7 MPa。 第2 个皮碗内侧位置和第4 个皮碗外侧位置受挤压严重, 提供过弯转向力。

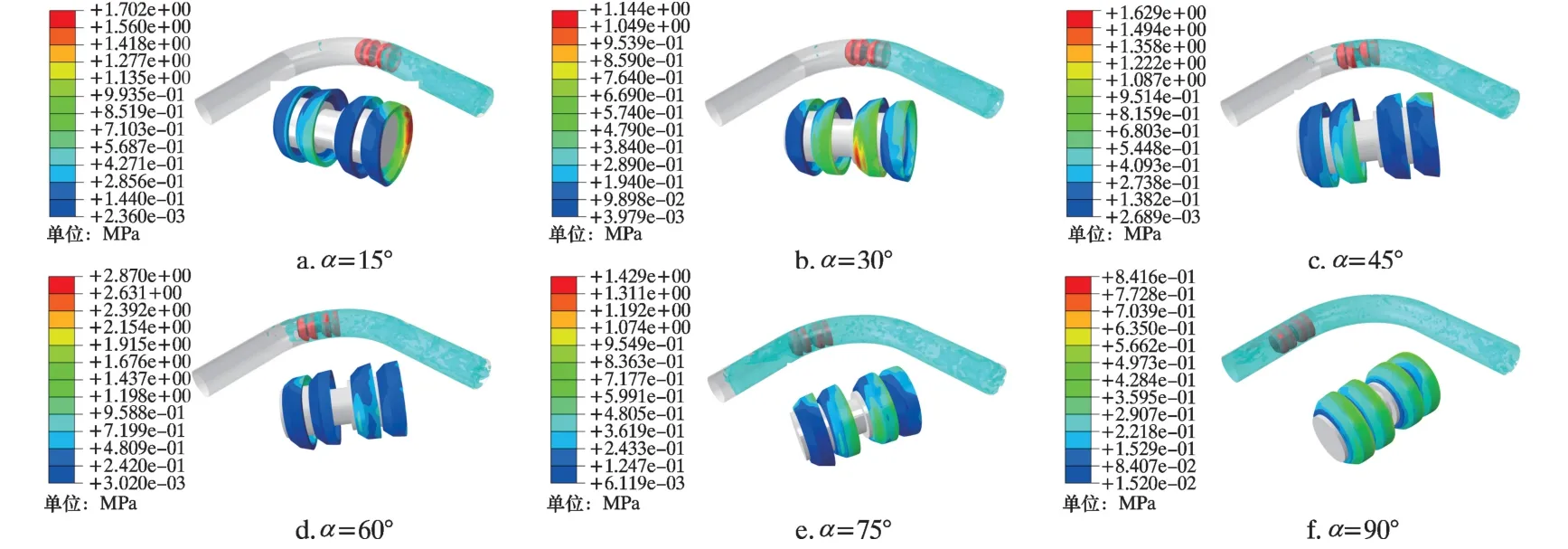
图6 过弯过程中6 个特征时刻的运行姿态及Mises 应力云图Fig.6 Running attitudes and Mises stress contours of the pig at six characteristic moments in the elbow-passing process

清管器运行至30°位置时, 第3 个皮碗内侧受挤压严重, Mises 应力大小为1.144 MPa, 接触面积因重力及摩擦力作用而增大, 皮碗根部前端与管道接触, 存在撕裂风险。 清管器运行至60°位置时, 因速度变化及转向需求, 第一个皮碗与管道内壁接触面积增大, 挤压程度加剧, Mises 应力达到2.87 MPa。 清管器运行至90°时, 清管器过弯完成, 进入竖直管段, 4 个皮碗所受Mises 应力基本相同, 主要以皮碗根部与管道内壁接触为主, 最大Mises 应力为0.84 MPa。

图7a 所示为清管器过弯过程中动力学响应情况。 清管器受流体推动力, 速度上升, 趋近于7 m/s, 进入直管段后速度下降趋于稳定, 波动于1～2 m/s 区间。 清管器进入弯管段后, 速度降至1 m/s 并稳定。 过弯过程中接触面积改变, 摩擦力增大导致憋压现象。 如图7b 所示, 清管器出弯时加速度骤增, 大小为1 700 m/s2, 清管器速度增大至3 m/s。 工程应用中同样存在该问题, 出弯后清管器以较高速度离开弯管, 高速将导致检测精度下降明显。

图7 清管器过弯速度和加速度变化情况及结构非连续特征面示意图Fig.7 Variation of elbow-passing velocity acceleration and discontinuous feature surface of the structure

本文创新性地提出结构非连续特征面定义, 目前国内皮碗尺寸设计缺少标准及相关规范, 为研究皮碗结构形式对过弯及通过性能的影响, 提出将皮碗外表面尺寸转折面作为结构非连续特征面ζ, 如图7c 所示, 分析该转折面结构对过弯性能的影响。研究结构非连续特征面时以过盈量4%管道为对象, 将转折面径向尺寸分别选取为2%～6%过盈量时对应尺寸。

为研究清管器结构对速度效应的影响情况, 本文分别从过盈量θ、 夹持率δ和结构非连续特征面ζ这3 个角度入手, 引入速度v、 加速度a及应变情况ε作为清管器通过性能评价指标。

2.2 通过性能评价指标影响因素分析

图8 所示为不同过盈量清管器过弯速度变化情况。 过盈量小于3%时, 过弯速度均大于3 m/s。过盈量为1%时平均速度为6.36 m/s, 仅用0.3 s即完成出弯。 分析原因, 清管器在发球阶段受尾部介质推动进入过盈管段后, 接触面积集中于皮碗边缘, 过弯速度未明显降低, 以较快速度通过弯管,过盈量为3%时平均速度达到4.16 m/s, 达到入口流速的416%。 过盈量大于4%时, 清管器进入过盈管道后速度迅速降至1 m/s 左右, 过盈量为6%时出弯速度骤增至5.8 m/s。 分析原因, 该过盈量范围管道憋压严重, 出弯后速度突变剧烈。

图8 过弯速度随过盈量变化情况Fig.8 Change of the elbow-passing velocity with the cup interference

图9 所示为清管器不同夹持率下过弯速度变化情况。δ=55%时平均速度最大, 大小为4.6 m/s,0.35 s 即完成过弯过程。 夹持率大于65%过弯速度波动明显, 65%时清管器进入弯头后速度逐渐波动趋于0.5 m/s, 0.53 s 时出弯后因憋压现象速度在短时间内增加至3.3 m/s。δ=70%工况过弯速度在0.5～3.0 m/s 范围内波动, 0.3 s 出弯后速度迅速升至5 m/s。 分析原因, 夹持率增大后, 皮碗自由端尺寸减小, 清管器心轴过弯时波动剧烈, 速度响应敏感。

图9 过弯速度随夹持率变化情况Fig.9 Change of the elbow-passing velocity with the clamping rate

图10 所示为清管器皮碗处于不同结构非连续特征面位置下过弯速度变化情况。 过弯速度随结构非连续特征面的增大而增加。 结构非连续特征面为2%位置工况的清管器过弯平均速度为0.54 m/s,是结构特征面位置为6% 时平均过弯速度的19.78%。 结构非连续特征面小于3%位置时, 出弯后速度突变现象不明显。 分析原因, 该组清管器过弯工况过盈量为4%, 当结构非连续特征面小于4%时, 皮碗与过盈管道接触位置处于特征面前部,皮碗进入过盈管道所需压缩量较大, 清管器过弯过程中摩擦力增加, 速度降低明显。

图10 过弯速度随结构非连续特征面变化情况Fig.10 Change of the elbow-passing velocity with the discontinuous feature surface of the structure

图11 为不同过盈量下清管器加速度变化情况。加速度呈现先减小后增加的趋势, 过弯时呈匀速状态, 出弯时因清管器尾部憋压严重, 6%过盈量工况瞬间加速度达到1 200 m/s2, 出弯结束后加速度迅速趋于0, 在竖直管段内保持匀速运动。

图11 过弯加速度随过盈量变化情况Fig.11 Change of the elbow-passing velocity acceleration with the clamping rate

图12 为不同夹持率下清管器加速度变化情况。与不同夹持率速度变化相对应, 夹持率大于65%时加速度波动大; 当夹持率为70%时, 平均加速度为214.28 m/s2, 是夹持率为50%的668.4%。皮碗夹持端尺寸过大导致皮碗变形能力降低, 速度波动剧烈。 当夹持率小于55%时加速度无明显波动, 过弯过程中未产生憋压现象, 出弯后速度提升量较小, 对检测效率影响程度轻微。

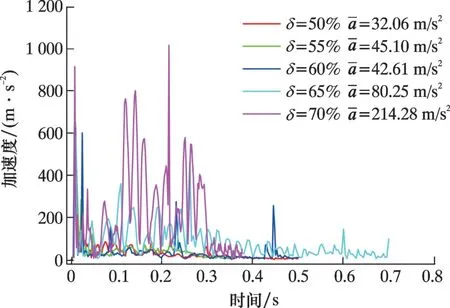
图12 过弯加速度随夹持率变化情况Fig.12 Change of the elbow-passing velocity acceleration with the clamping rate

图13 为不同结构非连续特征面位置下加速度变化情况。 当结构非连续特征面位于2%过盈量位置时, 接触面积集中于皮碗唇部以下, 清管器受力情况变化剧烈。 该工况过弯过程中加速度变化复杂, 平均加速度为57.99 m/s2。 结构非连续特征面位于皮碗唇部即位置大于4%时, 清管器加速度呈先上升后趋近于0 的趋势。

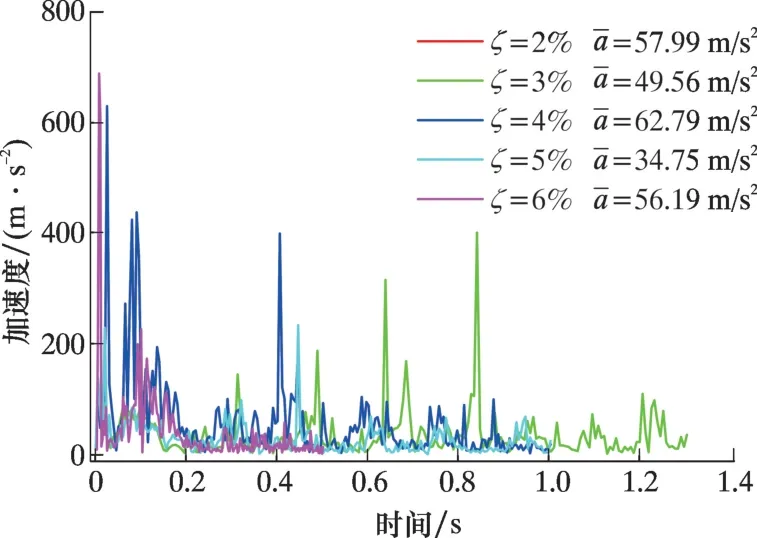
图13 过弯加速度随结构非连续特征面变化情况Fig.13 Change of the elbow-passing velocity acceleration with the discontinuous feature surface of the structure

图14 所示为3%过盈量工况清管器过弯过程中6 个特征时刻的运行姿态及应变云图。 由图14 可以看出: 15°时清管器主要以第四个皮碗的挤压为主, 转向力由尾部提供, 使清管器顺利进入管道,最大应变位置出现在第四个皮碗的特征面位置, 大小为0.122; 30°位置清管器应变集中于第二、 三皮碗的上半部, 最大应变为0.096; 45°位置与15°位置应变情况相似, 主要以第四个皮碗底部结构非连续特征面变形为主, 最大应变为0.103; 60°至75°位置皮碗变形集中在第一、 二皮碗的下半部分位置, 该位置清管器轴线偏向大曲率管道侧; 90°位置清管器出弯后进入直管段, 最大应变为0.07。

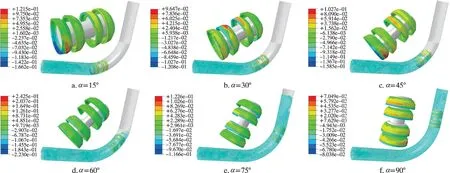
图14 过弯过程中6 个特征时刻的运行姿态及应变云图Fig.14 Running attitudes and strain contours of the pig at six characteristic moments in the elbow-passing process

分析可知, 清管器过弯过程中第四个皮碗底部结构非连续特征面位置应变较大, 皮碗存在破坏的风险。 为研究皮碗结构参数对应变的影响, 下文研究了过盈量、 夹持率与结构非连续特征面对应变的影响。

最大应变随过盈量变化情况如图15 所示。 过盈量小于3%时, 最大应变位置集中在第二个皮碗小曲率弯管内壁侧和第四个皮碗大曲率弯管内壁侧, 2 处位置受力产生应变以特征面处的拉应力为主。 过盈量大于3%时, 最大应变位置主要集中在第一个皮碗大曲率弯管内壁侧和第三个皮碗小曲率弯管内壁侧。 分析原因, 该范围工况通过弯头时清管器轴线偏向大曲率弯管侧, 第一个皮碗挤压情况较明显。 最大应变在过盈量小于3%时呈递增趋势, 过盈量大于3%时呈现先减小后增大的趋势,最大应变为0.13。

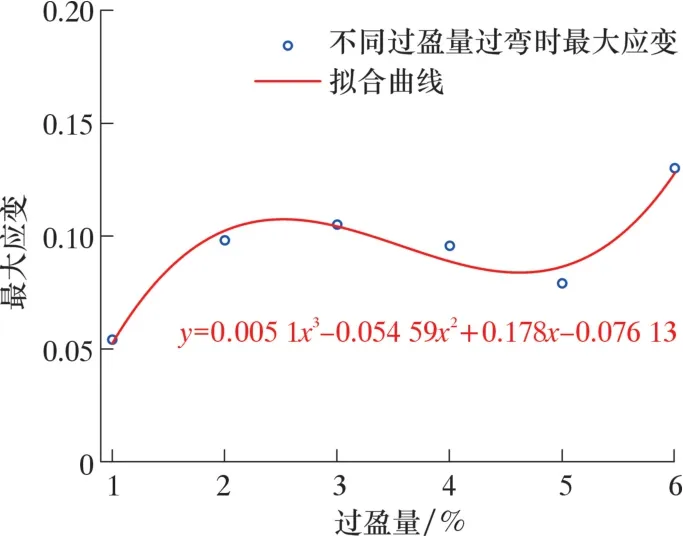
图15 最大应变随过盈量变化情况Fig.15 Change of the maximum strain with the cup interference

如图16、 图17 所示, 除夹持率65%工况应变主要集中于第二个皮碗小曲率弯管内侧及第四个皮碗大曲率弯管内侧外, 其他不同工况应变集中在第一个皮碗大曲率弯管内侧。 夹持率为60%时, 应变集中于第一个皮碗前侧夹持端,夹持面积较小,该处皮碗变形较大。 夹持率为65%时, 皮碗夹持端与自由端尺寸平衡, 应变情况稳定, 位置集中于第二个皮碗和第四个皮碗, 该工况最大应变仅为0.07。 夹持率为70%时, 皮碗自由端尺寸较小,可变形面积有限, 故应变集中于第一个皮碗外表面, 大小为0.12。 夹持率小于60%时, 清管器应变随夹持率的增大而升高, 60%夹持率时应变为0.19, 大于60%后应变呈单调递增趋势。 分析原因, 夹持率小于60%时皮碗自由端较大, 心轴姿态偏转小, 故皮碗变形情况较大, 夹持率大于60%时, 皮碗自由端面积减小, 心轴姿态偏转严重, 变形情况减小。

图16 最大应变随夹持率变化情况Fig.16 Change of the maximum strain with the clamping rate

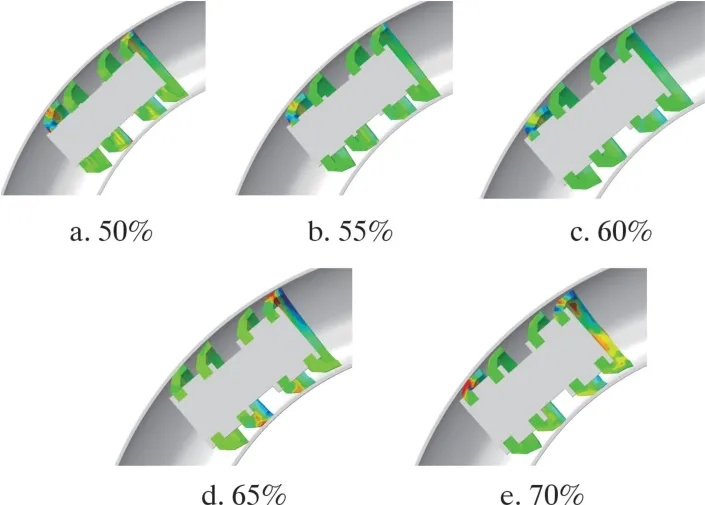
图17 不同夹持率下清管器应变云图Fig.17 Strain contours of the pig at different clamping rates

如图18 所示, 清管器皮碗应变情况及接触位置不随结构非连续特征面的改变而变化。 结构非连续特征面仅改变皮碗与管壁接触位置, 最大应变在0.09 上下浮动。

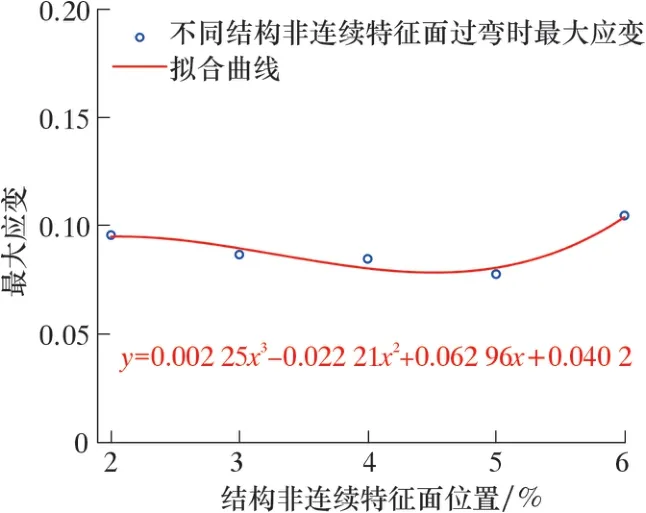
图18 最大应变随结构非连续特征面变化情况Fig.18 Change of the maximum strain with the discontinuous feature surface of the structure

3 结 论

(1) 清管器过弯时产生憋压现象, 速度降低。皮碗受管道挤压发生泄流, 与直管段相比摩擦力增大, 出弯后短时间内速度骤增, 影响相应管段检测效率。

(2) 过弯平均速度随过盈量的增加而减小,过盈量为1%时平均速度达到6.36 m/s, 较过盈量为6%工况清管器平均速度增加了390.2%, 清管器过弯平均速度受过盈量影响较为敏感。

(3) 夹持率为55%时清管器过弯平均速度最大, 大小为4.6 m/s, 呈现先增大后减小的趋势,夹持率为70%时因心轴偏转情况剧烈, 过弯平均速度出现上升。 当皮碗与管壁接触点在结构非连续特征面小于4%时过弯速度明显降低, 最低降至0.61 m/s, 影响清管器运动能力。

(4) 因过盈量影响皮碗边缘与管道内壁接触面积, 故加速度随过盈量增大呈现先降低再升高的趋势, 过盈量为5%时平均加速度最小, 仅为37.98 m/s2, 较过盈量为1%的平均加速度降低了47.5%。 因皮碗自由端面积较小, 夹持率为70%时清管器加速度波动较大, 平均加速度为214.28m/s2。 过盈量与夹持率的变化影响过弯过程中皮碗最大应变位置, 结构非连续特征面仅影响最大应变大小, 对位置无影响。

(5) 为提高清管器的90°过弯性能, 直径168 mm 清管器皮碗过盈量范围应在2%～4%之间, 夹持钢板对皮碗的夹持率应在60%左右, 皮碗几何非连续特征面设定原则应使皮碗与过盈管道接触位置集中于皮碗唇部位置。