基于熵产分析的套管稳定器结构参数优化
2023-06-15魏精波刘成文韦宝鑫卓景军李兆敏
魏精波 刘成文 韦宝鑫 卓景军 李兆敏
(1. 中国石油大学(华东) 石油工程学院 2. 中国石化集团中原石油工程公司)
0 引 言
套管钻井为直接利用套管替代常规钻井中的钻柱, 向钻头施加扭矩和钻压, 使钻进作业与下套管同时进行的钻井技术。 钻井完成后, 套管留下进行完井[1-3]。 与常规钻井相比, 套管钻井具有缩短钻进时间, 降低钻井成本, 减少钻井事故, 可保持钻井液的连续循环, 改善井控状况等优势, 在国内外取得了广泛的现场应用[4-7]。 和常规钻井中的钻柱稳定器类似, 套管稳定器是套管钻井过程中必要的部件, 主要起到扶正套管柱, 减少井壁与套管接箍之间的摩擦, 控制井斜, 提高井身质量与固井质量等作用[8-9]。 同时稳定器螺旋棱对钻井液起导流和限流作用, 钻井液通过稳定器产生周向分速度, 对环空流场发展、 岩屑举升上返速度有着显著影响[10-17]。 目前, 国内针对套管稳定器的研究非常少, 关于稳定器作用下的环空流场特性研究并不深入, 其设计主要参考钻柱稳定器与国内外已经现场应用的套管稳定器[18-19]。 因此, 深入研究套管稳定器与井眼之间的环空流场特性、 能耗与携岩规律很有必要, 对套管稳定器的设计乃至套管钻井作业的应用具有重要的实际意义。
笔者采用Fluent 软件对套管稳定器井段环空流场进行数值模拟, 利用熵产方法对流场产生的能耗进行分析, 得到流场的熵产分布特性和螺旋棱参数对能耗的影响规律; 并对套管稳定器的携岩能力进行分析, 得到螺旋棱参数对携岩的影响规律; 最后综合考虑能耗和携岩2 方面因素, 对螺旋棱参数进行优化, 优选出套管稳定器的结构尺寸。 所得结果可为套管稳定器优化设计和现场应用提供参考。
1 几何模型与网格划分
本文选取ø178 mm 具有3 条螺旋棱的套管稳定器, 如图1 所示, 具体尺寸见表1。 井眼直径为241.3 mm, 模型长度取1 500 mm, 将模型进行了适当加长, 以消除模型出入口边界条件对稳定器流场的影响。
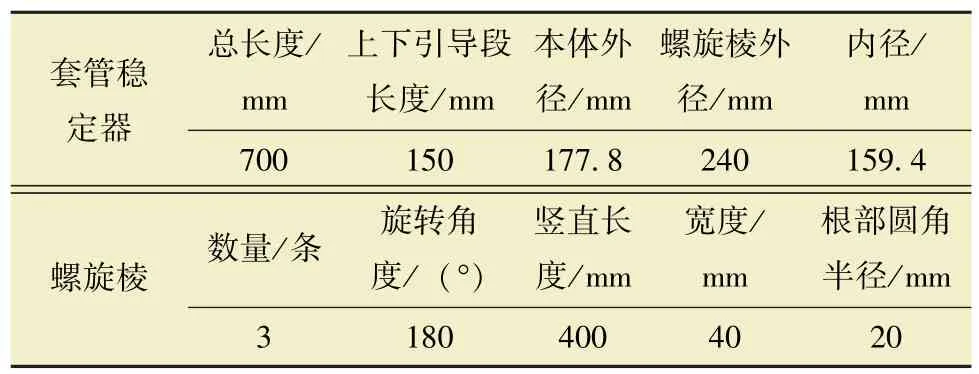
表1 套管稳定器的尺寸Table 1 Dimensions of casing stabilizer
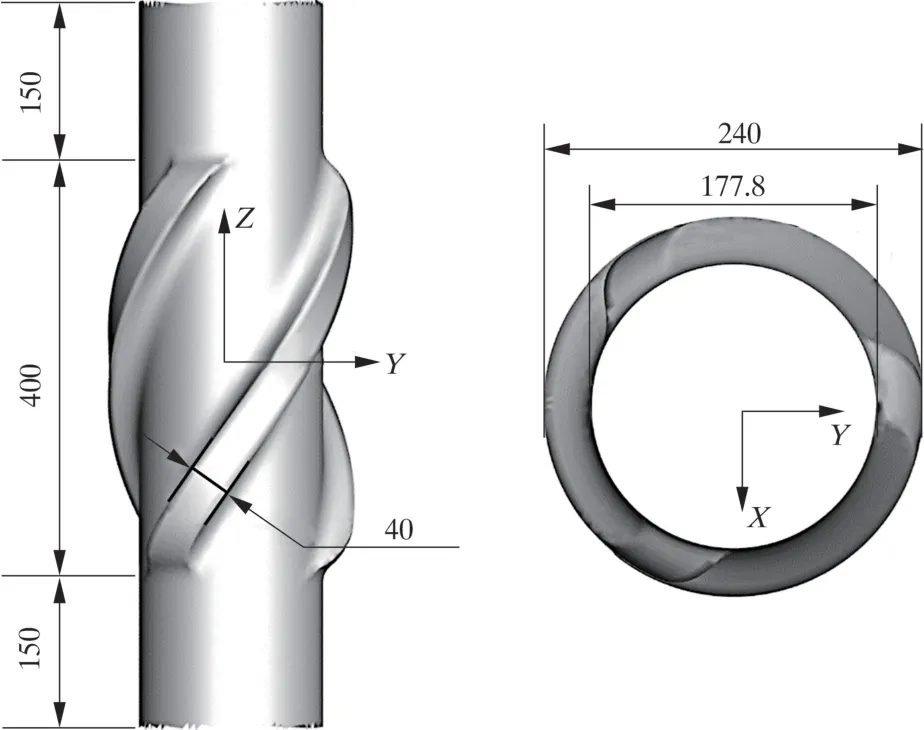
图1 套管稳定器的三维模型Fig.1 Three-dimensional model of casing stabilizer
采用Gambit 中的TGrid 方法对模型划分网格。为了进行网格无关性检验, 选择286 042、 409 388和526 475 这3 种网格单元数量进行计算, 对螺旋棱下端横截面Y轴方向直径上的轴向速度分布进行比较, 结果如图2 所示。 由图2 可知, 3 种网格数量的计算结果无明显差别, 因此本文采用286 042 个网格进行计算。
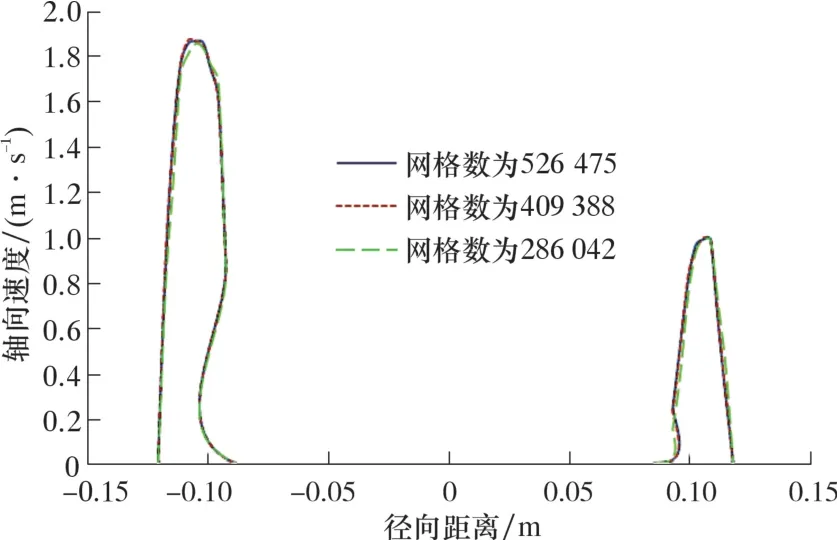
图2 模型网格无关性检验结果Fig.2 Test results of meshing independence of the model
2 数值方法
2.1 控制方程
环空中钻井液的流动为等温不可压缩非牛顿幂律流体湍流运动, 其本构方程为:
式中:τij为黏性应力, Pa;K为稠度系数, Pa·sn;n为流性指数, 无量纲;Sij为应变率张量, s-1;S2为应变率张量的第二不变量。
连续性方程:
式中:为钻井液时均速度, m/s;xi为位置坐标, m。
动量方程:
式中:为钻井液时均速度, m/s;xj为位置坐标, m;ρ为钻井液密度, kg/m3;为时均压力,为雷诺应力, Pa;为单位质量的重力, m/s2。
套管稳定器作用下的环空流场为螺旋流场, 环空几何形状极不规则, 这使得流动状态往往呈现湍流状态[19-21]。 本文采用标准k-ε模型湍流模型进行模拟, 其湍动能k和湍能耗散率ε的输运方程如下:
式中:k为湍动能, m2/s2;ε为湍动能耗散率,m2/s3;μt为湍动黏度, Pa·s;μ为钻井液表观黏度, Pa·s;σk和σε分别为与湍动能k和耗散率ε对应的Prandtl 数,σk=1.0,σε=1.3;Gk为平均速度梯度引起的湍动能产生项, Pa/s;δij为Kronecker delta 符号, 当i=j时δij=1, 当i≠j时δij=0;Cε1、Cε2、Cμ为经验常数,Cε1=1.44,Cε2=1.92,Cμ=0.09。
环空流动实际上为钻井液与岩屑的两相流动问题, 本文流场模拟中的岩屑颗粒体积分数小于10%, 故采用DPM 模型[22]。 DPM 模型通过求解颗粒作用力方程来得到离散相轨迹, 颗粒的作用力平衡方程为:
式中:dp为岩屑颗粒直径, m;CD为曳力系数,无量纲;Re为相对雷诺数, 无量纲。
而对岩屑颗粒轨迹的计算通过下式得到:
2.2 边界条件及计算方法
如图1 所示, 取Z轴朝上为正方向, 将模型下端设置为速度入口, 钻井液流量为40 L/s, 对应环空入口流速为1.9 m/s, 计算得到环空流体雷诺数Re为5 062.7; 设置模型上端为自由出口, 重力加速度沿Z轴负方向为9.81 m/s2。 岩屑入口初始质量分数为0.3%, 岩屑入射速度与钻井液保持一致, 值为1.9 m/s。
钻井液密度ρ为1 200 kg/m3, 稠度系数K为0.19 Pa·sn, 流性指数n为0.66[23], 岩屑密度为2 500 kg/m3, 粒径为3 mm, 入口岩屑质量分数为0.3%对应的岩屑质量流量为0.144 kg/s[11-20], 钻井液温度为298 K。
采用有限体积法对钻井液流动控制方程进行离散, 压力插值算法采用Standard, 空间离散选择二阶迎风格式, 压力-速度耦合采用SIMPLEC 算法,既能保证较高的计算精确度, 同时又有较高的计算速度。
2.3 熵产分析方法
熵产表征的是一个不可逆的热力学过程中的能量损失。 湍流流动的熵产由2 部分组成, 即为基于时均运动的黏性熵产和基于脉动运动的湍流熵产[24]。 仅考虑流动, 不考虑温差传热, H. HERWIG 等[25]给出了流场中的熵产计算公式, 其中黏性局部熵产率公式为:
由于脉动速度场不易测量和计算, H.HERWIG等[25]同时也给出了用湍能耗散率代替脉动速度场求解湍流熵产的方法, 其湍流局部熵产率公式如下:
由式(12) 和式(13) 相加可得到总的局部熵产率计算公式:
3 结果分析与讨论
3.1 环空流场特性
图3 为套管稳定器环空内钻井液的流场速度分布云图。 由图3 可以看出, 由于螺旋棱的导流作用, 螺旋流道会使钻井液速度产生切向旋转分量,钻井液沿螺旋流道螺旋上升, 使得稳定器螺旋流道内的速度比下部入口速度大。 这是因为稳定器的螺旋棱结构使得环空流道面积减小, 从而导致钻井液流速增大。
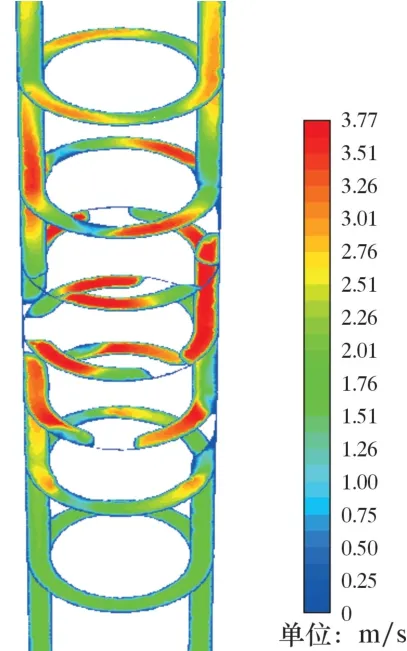
图3 环空流场速度云图Fig.3 Velocity contour of the annular flow field
3.2 熵产分析
图4 和图5 分别为稳定器壁面以及环空流场内部的局部熵产率分布云图。 图4a 和图5a 表明, 黏性熵产主要发生在螺旋棱外缘与井壁之间的狭小空隙中, 稳定器螺旋流道内的黏性熵产次之, 约为间隙处的几十分之一。 这主要是由于螺旋棱与井眼的间隙仅1 mm 左右, 钻井液的流动横截面积非常小, 流体间的黏性摩擦急剧增加, 黏性耗散增加,导致这一区域的黏性熵产很大。 而图4b 和图5b 表明, 湍流熵产主要发生在螺旋流道入口以上的螺旋棱下端附近, 而螺旋流道内的湍流熵产相对较低,螺旋棱外侧与井眼之间的间隙内也是湍流熵产较高的区域。 这是因为当钻井液到达螺旋流道入口时,因螺旋棱的限制, 流体的有效流动面积急剧减小,流动速度升高, 壁面速度梯度增大, 湍流紊动增强, 导致湍流熵产增加。
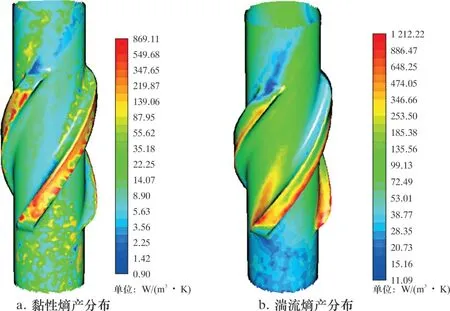
图4 稳定器壁面上局部熵产率分布云图Fig.4 Contours of local entropy generation rate on the stabilizer wall
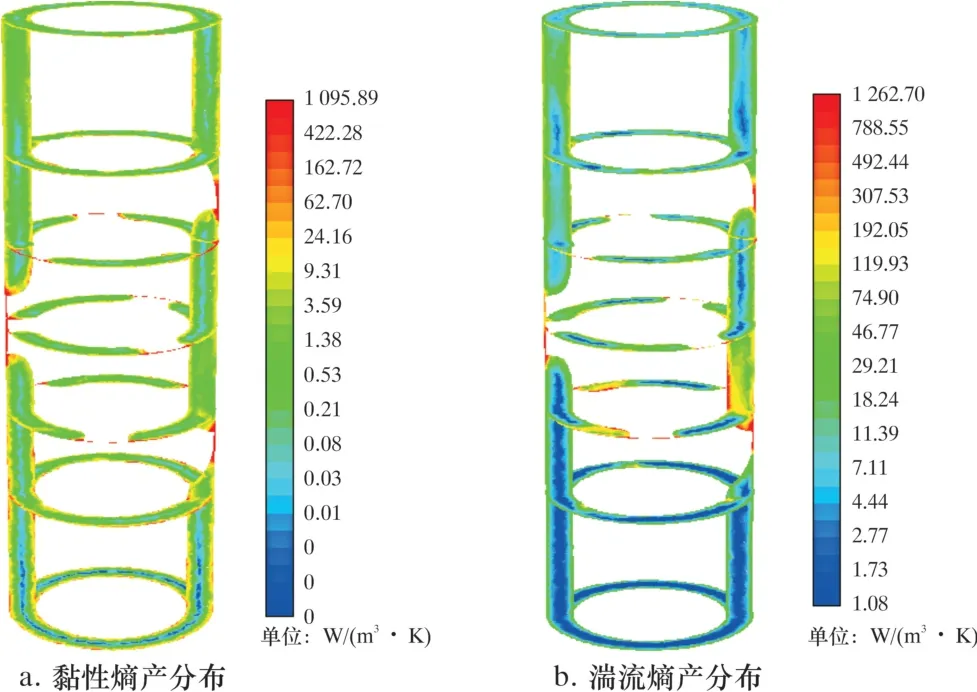
图5 环空流场内局部熵产率分布云图Fig.5 Contour of local entropy generation rate in the annular flow field
表2 为钻井液经过套管稳定器整个模型环空体积内的各项熵产率和总熵产率计算结果。 由表2 可以看出, 湍流熵产率在总熵产率中占的比例较大,占76.4%, 黏性熵产率占比为23.6%, 黏性熵产是次要的。
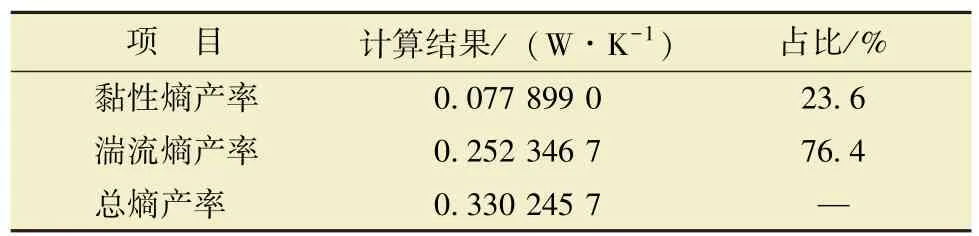
表2 环空总熵产率计算结果Table 2 Calculation results of the overall entropy generation rate in the annulus
3.3 携岩分析
图6 为套管稳定器壁面附近和环空内岩屑浓度分布云图。 由图6a 可知, 在螺旋棱的分流限流下,大部分岩屑均随钻井液一起螺旋上升, 但由于螺旋棱的阻碍作用, 有部分岩屑在螺旋棱根部发生堆积, 岩屑浓度显著增大。 另一方面, 由于钻井液在进入螺旋流道后速度升高, 促使岩屑上返速度也升高。 从图6b 可以看出, 随着岩屑上升, 过流截面的岩屑质量浓度逐渐增大, 且同一截面上, 环空外壁面的质量浓度逐渐增大, 内壁面附近的岩屑质量浓度逐渐减小。 这是岩屑在进入螺旋流道后受离心效应作用被甩向外壁的结果。 总体上看, 套管稳定器的螺旋棱结构对岩屑上返有利, 有效地提高了岩屑的上返速度和携岩效率。 由此可见, 螺旋棱对套管稳定器的能耗和携岩能力有较大影响。
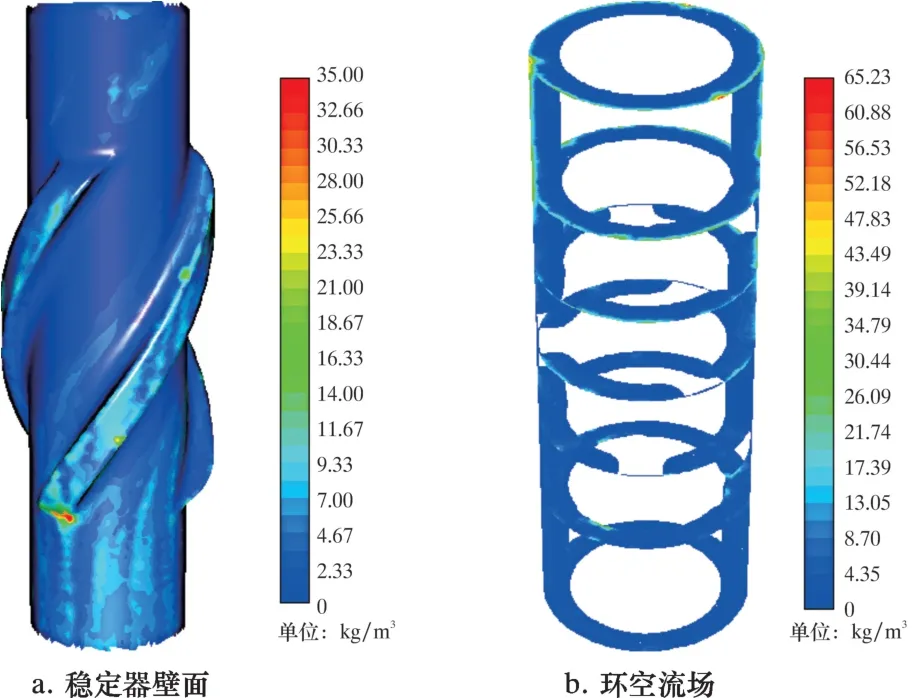
图6 稳定器壁面附近和环空内岩屑浓度分布云图Fig.6 Contour of cutting concentration near the stabilizer wall and in the annulus
3.4 螺旋棱结构参数优化
3.4.1 携带比的表征
由于螺旋棱的导流、 限流作用, 钻井液在螺旋流道内形成涡流, 从而搅动并携带岩屑上返[26]。在环空内, 岩屑上返速度取决于钻井液上返速度与岩屑自身滑落速度之差, 即:
式中:vp为岩屑净上返速度, m/s;vt为钻井液上返速度, m/s;vs为岩屑滑落速度, m/s。
上式两边同时除以vt可得:
通常将vp/vt称为携带比, 并用该比值来表征岩屑的清洁效率[27-28]。 另一方面, 从上文可知,岩屑容易在螺旋棱根部发生堆积, 影响了螺旋棱的携岩能力, 应想办法减轻岩屑堆积现象。 因此, 下文将根据岩屑携带比、 螺旋流道入口岩屑最大质量浓度以及环空熵产等3 个参数, 对螺旋棱的结构参数进行设计和优化。 其中, 采用钻井液和岩屑的断面平均轴向速度计算岩屑携带比, 计算断面选取在上引导段出口。
3.4.2 螺旋棱竖直长度的优化
图7 为岩屑携带比、 螺旋流道入口岩屑最大质量浓度以及环空熵产3 个参数随螺旋棱长度的变化规律。 由图7a 可知, 岩屑携带比随螺旋棱长度的增加而逐渐下降, 而入口岩屑最大质量浓度先增加后减小, 在螺旋棱长度为400 mm 时出现极大值。这是因为随着螺旋棱竖直长度的增大, 岩屑在螺旋棱流道内上升时受到的离心效应越久, 积聚在外壁, 受到外壁和其他岩屑颗粒的相互作用, 影响了岩屑上返速度。 从图7b 可以看出, 黏性熵产率随螺旋棱竖直长度的增加而缓慢增加, 湍流熵产率与总熵产率随螺旋棱竖直长度增加而明显下降, 直到螺旋棱长度大于400 mm 后这一趋势才有所减缓,且湍流熵产率在总熵产率中的占比亦明显降低。 这是因为随着螺旋棱竖直长度的增加, 流动空间体积逐渐减小, 但受螺旋棱壁面影响的速度梯度增大的空间区域增加, 导致黏性熵产增大; 而由于流动空间体积变小, 导致湍流区域也减小, 使得湍流熵产减小, 湍流熵产降低幅度大于黏性熵产增加的幅度, 最终总熵产逐渐降低。
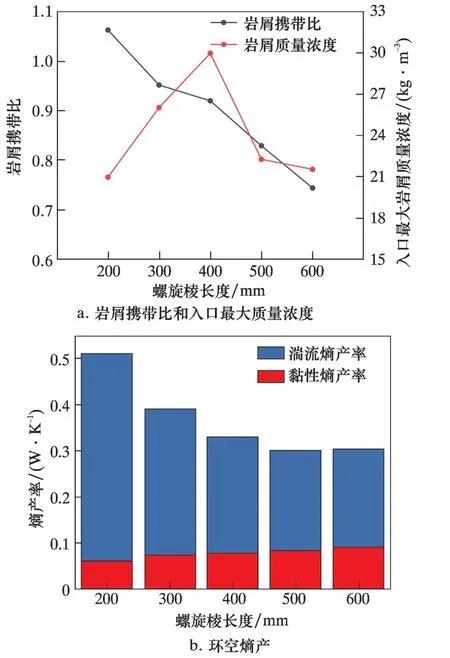
图7 各参数随螺旋棱长度变化规律Fig.7 Variation of parameters with spiral edge length
当螺旋棱长度在300 mm 时, 岩屑携带比较大而能耗相对较小, 同时入口岩屑堆积现象也相对较小。 如果继续加长螺旋棱, 能耗下降的幅度较小,但岩屑携带比下降幅度较大, 不利于携岩。 因此,综合能耗低、 岩屑携带比大以及岩屑堆积少的要求, 螺旋棱长度选300 mm 为佳。
3.4.3 螺旋棱宽度的优化
图8 为岩屑携带比、 螺旋流道入口岩屑最大质量浓度以及环空熵产随螺旋棱宽度变化规律。 由图8a 可知: 岩屑携带比整体上随螺旋棱宽度的增加而增加, 当宽度在40 mm 时, 携带比达到极大值;螺旋流道下端入口的岩屑最大质量浓度随螺旋棱宽度的增加而增大, 说明螺旋棱宽度的增加会使螺旋棱根部的岩屑堆积增加。 图8b 表明, 随螺旋棱宽度增加, 湍流熵产率明显增大, 而黏性熵产率虽有一定的增加趋势, 但变化并不大, 数值也较小。 这主要是因为螺旋棱宽度增加, 有效流道面积会显著降低, 流道内的钻井液流速明显增大, 带动岩屑上返速度升高, 螺旋流道内的湍流脉动和流体间的黏性摩擦均增强, 流道内的黏性耗散与湍流耗散均增加, 导致环空中的熵产尤其是湍流熵产明显增大。尽管螺旋棱宽度在30 mm 时的岩屑携带比较低,但其能耗和岩屑堆积较少。 综合考虑能耗和携岩2方面因素, 选择螺旋棱宽度为30 mm。
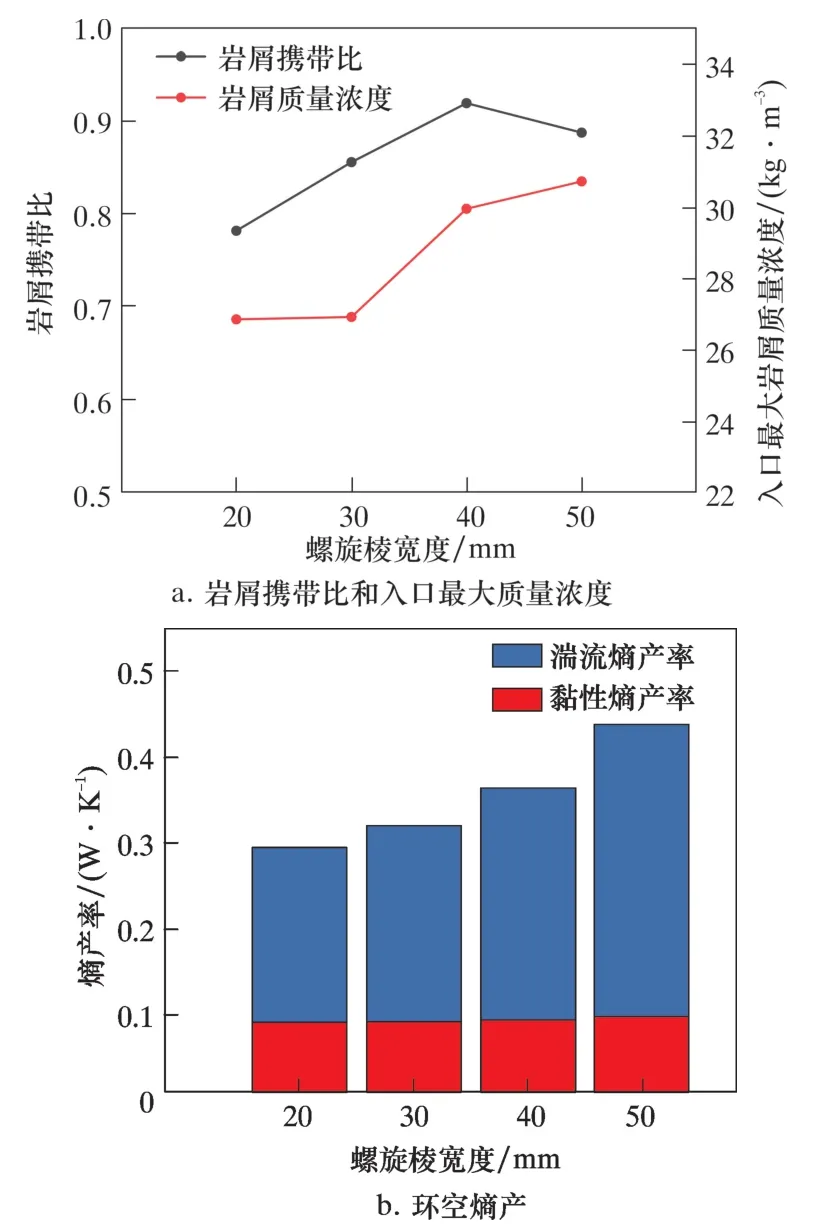
图8 各参数随螺旋棱宽度变化规律Fig.8 Variation of parameters with spiral edge width
3.4.4 螺旋棱根部圆角的优化
图9 为岩屑携带比、 螺旋流道入口岩屑最大质量浓度以及环空熵产随螺旋棱根部圆角半径的变化规律。 岩屑携带比随圆角半径的增大, 呈先增大后减小的趋势, 但整体变化幅度不大。 螺旋流道入口的岩屑最大质量浓度随螺旋棱根部圆角半径的增大而显著降低, 这说明螺旋棱根部圆角半径的增大对螺旋棱根部的岩屑堆积现象有明显的减弱作用。 黏性熵产率基本不随螺旋棱根部圆角变化而变化, 而湍流熵产率随螺旋棱根部圆角半径的增大逐渐增大, 但变化幅度较小, 因此螺旋棱根部圆角对环空能耗的影响非常小。 考虑到圆角半径为25 mm 时的能耗增加不是很大, 但岩屑携带比较高且入口岩屑最大质量浓度较低, 故选择螺旋棱根部圆角半径为25 mm。
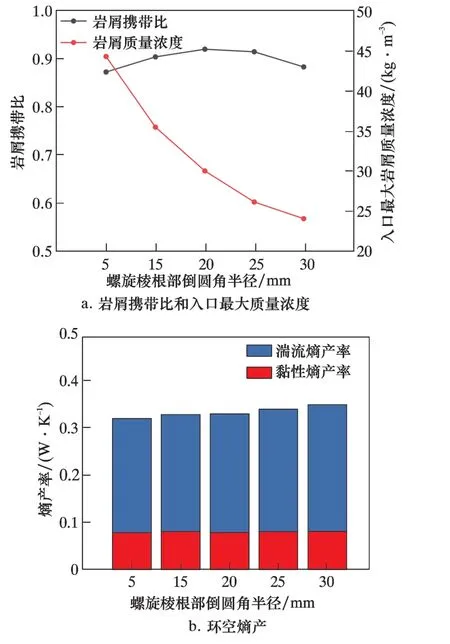
图9 各参数随圆角半径变化规律Fig.9 Variation of parameters with fillet radius
3.5 稳定器结构参数优化结果
根据上述螺旋棱参数对熵产和携岩能力影响规律的分析, 结合ø178 mm 套管钻井的现场实际,确定套管稳定器的结构尺寸如表3 所示。
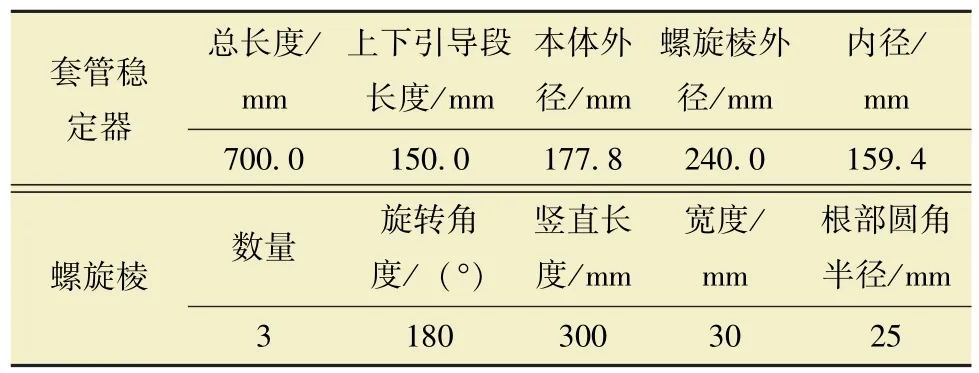
表3 优选出的套管稳定器结构尺寸Table 3 Optimized structural dimensions of the casing stabilizer
4 结 论
(1) 在套管稳定器的环空熵产中, 湍流熵产主要发生在螺旋流道入口附近的流道壁面以及螺旋棱外缘与井眼的狭小间隙内, 其在总熵产中占的比例较大; 黏性熵产主要发生在螺旋棱外缘与井眼的狭小间隙内, 其在总熵产中所占的比例较小。
(2) 套管稳定器井段环空内总熵产随螺旋棱长度的增大而减小, 随螺旋棱宽度增大而增大, 但其受螺旋棱根部圆角的影响很小。 螺旋棱根部会产生少量岩屑堆积, 适当增大螺旋棱根部圆角可明显减轻岩屑堆积。
(3) 综合对套管稳定器的环空能耗与携岩效果的分析, 优选出了ø178 mm 套管稳定器结构尺寸: 3 条螺旋棱分别旋转180°, 竖直长度为300 mm, 宽度为30 mm, 根部圆角半径为25 mm。 这种结构尺寸的套管稳定器能耗较小, 岩屑携带比较高且岩屑堆积程度较弱, 综合性能较好。
