指向初中生数学推理能力培养的问题链教学设计

朱金霞

【摘要】推理能力是学生数学学习能力的重要体现，在初中数学教学中，教师需要巧妙设计课堂问题，培养学生的推理能力，促进学生数学思维的发展.在实践教学中，教师可以设计问题链，结合一个主题布置多个问题，强化学生在课堂上的思考，优化课堂教学效果.本文立足于初中学生的数学推理能力，分析问题链教学设计的现实意义，提出具体的实践路径.

【关键词】初中数学；问题链；教学设计

1 指向初中生数学推理能力培养的问题链教学设计的现实意义

1.1 助推数学思维发展

问题链教学设计能够将教学内容以问题的形式串联起来，对数学知识结构进行表示，这有利于推动学生数学推理能力的发展.在问题链的设计和应用中，教师可以为学生提供冷静思考的时间和空间，学生能够独立发现、独立探索，不断提高数学推理能力，获得数学思维的发展.

1.2 实现知识深度理解

通过采用问题链教学法，教师能够将数学知识按照难易程度进行排列，然后设计相对应的问题，让学生参与到思考活动中，通过数学问题构建新知识，使自身的知识网络结构更加完善，实现深层次学习.在问题的引导下，学生能够主动思考、主动建构，学习效果能够得到全面提高.

1.3 降低问题推理难度

通过运用问题链教学法，教师能够结合教学内容设计一系列的数学问题，单个问题的难度有所降低.在问题链教学中，每个小问题都是后面大问题的铺垫，数学问题由浅入深、层层递进，学习任务能够得到分解，数学推理的难度系数能够得到降低.

2 指向初中生数学推理能力培养的问题链教学设计原则分析

2.1 确保问题间的阶梯性

在设计问题链时，教师首先要确保问题之间的阶梯性，使问题链的设计由简单到复杂，层层深入，这样学生才能在解答问题的过程中获得思维的训练.数学教师需要把握好问题和问题之间的衔接，同时还要留出一定的思考空间，使问题具备一定的难度.除此之外，教师在设计数学问题时，还要适当布置探究类的问题，要求学生在课堂上进行思考、讨论、计算，让学生通过实践提高数学学习效果，全面增强数学学习的自信心.

2.2 基于教学目标的设计

在课堂教学中，问题链应该贯穿于整个教学活动，所有问题的设计都要围绕教学目标，这样才能防止问题偏离主要方向，以更好地达成教学目标.因此，在设计数学问题时，教师首先要认真思考学生需要在课堂中获得哪些能力，然后再确定问题链的主题.在设计问题链时，教师需要确定出主问题、子问题，通过导入、启发、应用等方法，发挥整个问题链的作用，通过问题链培养学生的推理能力，让学生掌握重要的数学知识点，提高解题能力.

2.3 建立新旧知识的联系

初中数学课程的系统性较强，学生的数学知识基础决定了后期新知识的学习.为此，教师需要全面分析学生先前掌握的知识，包括数学基本概念、数学原理等，然后引导学生完成知识迁移，培养学生的推理能力.在问题链的设计中，教师需尽量缩小知识之间的跨度，划分问题的难度层级，在初始阶段可以设计复习性的问题，或者创设问题情境，然后由旧知识引入新知识，帮助学生理解新的数学概念，开展课堂解题练习.

3 指向初中生数学推理能力培养的问题链教学设计的现实路径

3.1 合情推理类问题链设计

合情推理是一种结合数学定义、事实、命题的具体内容开展的数学推理，这种推理具有较强的启发性，在推理过程中需要做到具体情况具体分析，学习者需要不断向自己提出启发性的问题，使自身思维获得发展.

3.1.1 类比推理

类比推理是合情推理的一种，在初中数学教学中，教师需要培养学生的类比推理能力，引导学生根据学过的旧知识总结新知识，强化知识迁移，让学生在推理中获得成就感和自信心，实现探究式学习.

例如 在学习七年级下册“不等式”时，教师可以将不等式的性质与等式的性质结合起来.为此，教师可以设计如下问题链：

问题1 一对双胞胎兄弟比较身高，两人提出了多种比较方法，第一种是两个人都站在第一级台阶上，第二种是哥哥站在平地上，弟弟站在台阶上，第三种是两人都站在平地上.哪种比较方法是公平的？为什么？

分析 通过真实情境，学生能够分析出比较身高的方法，明确公平的含义，在这一情境下，要么两个人同时站在同等高度的台阶上，要么两个人站在平地上，这样才能确保公平.通过思考问题，学生可以联想到等式的相关知识.

问题2 哥哥和弟弟站在平地上一样高，现在两人都站在台阶上，相当于两个人的身高同时增加了相同的高度，这可以让我们联想等式的性质，如果a＝b，那么a±c＝b±c，结合等式的性质，你能否对不等式的性质进行猜想？

分析 通过猜想、类比，学生可以根据等式的性质得出不等式的第一条规律.

问题3 在不等号的两侧同时加上或者减去一个整式，得到的式子将会满足哪种关系？请举例说明.

分析 在问题3中，学生可以用计算验证自己的猜想，进一步总结不等式的第一条性质.

问题4 在以前的学习中，我们曾经学习过等式的规律，等式两边同时乘以一个数或者除以一个不等于0的数，等式依然成立.通过类比，你能得出不等式的规律吗？

分析 学生需要对一个不等式展开计算，在不等式两边同时乘以一个正数，得出不等式的第二条性质：如果a＞b，c＞0，那么a/c＞b/c（或a/c＞b/c）.另外，学生还需要在不等式的两边同时乘以或者除以一个负数，得出不等式的第三条性质：如果a＞b，c＜0，那么a/c＜b/c（或a/c＜b/c）.

學生可以通过实践探究和类比推理，得出不等式的性质，提高类比推理能力.

问题5 对等式的性质和不等式的性质进行分析，你可以发现什么不同点？

分析 通过问题5，学生可以将等式的知识迁移到不等式中，再把不等式的性质应用于生活中，进一步完成知识迁移.

3.1.2 归纳推理

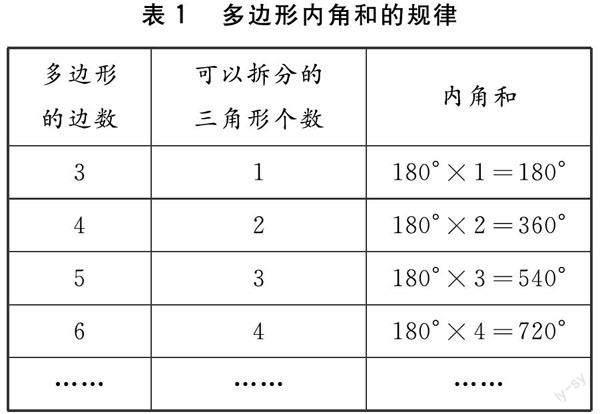
在开展归纳推理时，教师同样可以应用问题链教学法.例如，在学习八年级上册“多边形及其内角和”时，教师可以让学生从三角形内角和、多边形内角和的归纳中发现最普遍的规律，设计如下问题链.

问题1 三角形内角和是多少？

问题2 四边形可以裁剪成几个三角形？如何通过三角形内角和推导四边形的内角和？

问题3 同样应用拼接法，你可以得出五边形、六边形的内角和吗？

问题4 将三角形、四边形、五边形、六边形的内角和知识总结起来，你可以发现多边形内角和的规律吗？

通过引入问题链教学法，教师可以将课堂教学中的关键知识点融合到问题链中，组织学生进行归纳和总结，让学生在归纳的过程中掌握多边形内角和的规律，从而加强对多边形知识的学习.通过归纳推理，学生可以树立探究学习的意识，减少对教师的依赖，通过实践的方法发现数学知识的规律.

3.2 演绎推理类问题链设计

合情推理能够帮助学生获得一些猜想，加强学生对结论的认识，而演绎推理能够帮助学生进一步验证结论的真假，从这个角度上来说，合情推理和演绎推理之间是相辅相成的关系，教师需要在实践教学中重视演绎推理与合情推理的结合，引导学生通过演绎推理证明数学结论，建立数学知识体系，促进学生思维发展.演绎推理是指从一般性的原理出发，推出某个特殊情况的结论.在初中数学教学中，教师需要通过问题链开展教学，引导学生分析“大前提”和“小前提”，最终得出结论，对特殊的情况进行判断.

例如 在学习“解一元一次不等式”时，学生已经掌握了不等式的基本性质，拥有了一元一次方程的知识基础，教师就可以将二者结合起来，设计问题链，培养学生的演绎推理能力.

问题1 回忆不等式的性质，分析解方程的步骤.

分析 学生可以在问题的指导下回忆基础知识，梳理不等式的三条性质，明确解方程的步骤——去分母、去括号、移项、合并同类项、系数化为1.

问题2 解一元一次方程15－3x=x－1；解一元一次不等式15－3x＞x－1.

问题3 解一元一次方程5（x+1）=3（2x+5）；解一元一次不等式5（x+1）＞3（2x+5）.

问题4 解一元一次方程（x+4）/3-（3x-1）/2＝1；解一元一次不等式（x+4）/3-（3x-1）/2＞1.

通过设计问题链，学生能够总结出解一元一次不等式的一般步骤，应用演绎推理的方法掌握一元一次不等式的解法，将一般性的原理应用于特殊问题上.从学生的角度来说，解答数学问题的过程就是学习数学知识、探究数学规律的过程，在学习解一元一次不等式时，学生可以在课堂上进行计算，在计算的过程中与一元一次方程做对比，采用演绎推理的方法进行学习，提高思维的灵活性，提高对知识的学习效果.

4 结语

当前，很多初中学生缺乏数学推理能力，在面对推理问题时缺乏主观能动性，无法通过类比、归纳、演绎等方法自主探究知识，数学学习的依赖性较强.在初中阶段，只有学生具备一定的数学推理能力，才能自主分析数学问题，开展数学猜想，深入揭示数学概念的本质，强化实践操作.在课堂教学当中，教师可以应用问题链教学法，结合教学目标，设计一系列的数学问题，把握好问题的难易程度，确保问题由简单到复杂，层层递进，使学生依靠问题链进行思考，提高数学学习效果.

【课题：江苏省教育科学“十四五”规划重点课题《指向初中生代数推理能力发展的问题链设计研究》，项目编号：C-b/2021/02/01】

参考文献：

[1]曹传秀.巧用问题式探究激活初中數学课堂[J].中国教育学刊，2022（S1）：127-129.

[2]孙雅琴.问题导向：初中数学深度教学的实践研究[J].数学通报，2020（11）：35-39+44.

[3]娜仁格日乐，史宁中.数学学科核心素养与初中数学内容之间的关系[J].东北师大学报（哲学社会科学版），2019（06）：118-124.

[4]韩方廷.新课标下初中数学课堂教学有效性策略分析[J].中国教育学刊，2019（S1）：54-56.

[5]冯启磊.基于学生猜想探究能力发展的初中数学教学改进研究[J].教育科学研究，2018（03）：66-70.

[6]李灿钊.初中数学教学要注重学生综合应用能力的培养[J].中国教育学刊，2017（06）：106.