巧设提问深度,落实教学深度
2023-06-14林蓉蓉鲍建立
林蓉蓉 鲍建立


【摘要】课堂提问在数学教学中是非常普遍而又极为重要的教学方式,它在每天的课堂教学中突显着古老而又崭新的魅力.所以教师在课堂上不能随意、无目的、频繁地提问.课堂上教师需要巧设提问的深度,才能落实教学的深度.
【关键词】初中数学;课堂教学;深度提问
如何进行深度教学,对一线教师来说是一个考验.教學过程中教师的作用不是“告诉”知识,而是“激发”学生的学习潜能,“激励”学习热情,“引领”处事方法、态度、价值观和综合能力.要在课堂中比较好的开展深度教学,笔者认为在课堂上进行深度提问,能够有效地落实深度教学.教师只有课前精心设计问题,并巧妙的提问,才能培养学生的思维能力.本文以“2.7探索勾股定理”为例,谈一谈如何具体开展深度提问,让我们做到真正的深度教学.
1 及时追问,引发深度思考
如何引发学生的思考?显然离不开老师的引导和提问.“思促学,疑激思”.问题是触发学生思维的引线,也是学生学习内驱力得以迸发、探索创新得以实现的导火索.
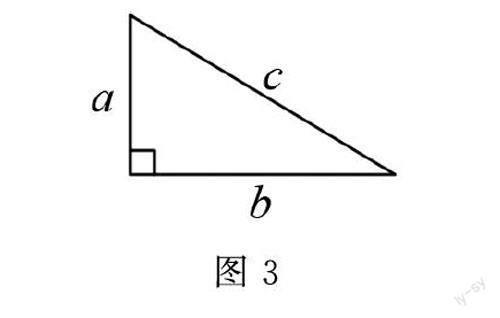
例:每个小组发了四个全等的直角三角形,让学生通过动手实践和小组合作研究.
问1:如何用四个全等的直角三角形纸片,拼成的一个大的正方形(仅允许中间有空隙).
在学生拼成如图1后,再次提问.
问2:“还有其他的拼法吗?”通过这样的追问可以引发学生去思考还可以怎么拼?
得到两种拼法之后,继续追问.
问3:“你拼成的一定是正方形吗?”启发学生思考怎么去证明拼的就是正方形?再追问.
问4:“这个大正方形的面积可以怎么表示?”
问5:“除了直接利用公式来计算还有别的想法吗?”从而轻松地证明勾股定理.
问6:是不是勾股定理中的三边关系都一定表示成a2+b2=c2呢?
通过问拼一拼,结合老师的及时追问,一步一步催生学生的思考,让学生先拼出正方形,然后证明正方形,再用不同的方法表示正方形的面积,利用等积法,水到渠成地证明了勾股定理.让学生从动手动脑到动口,通过一系列的追问,引导学生积极主动地参与到课堂中来,激发学生的学习热情,证明勾股定理的过程一气呵成.利用勾股定理来解决问题时,以往经常有学生直接把a2+b2=c2等价于勾股定理,这是学生的易错点,老师此时的追问,可以引起学生联想刚才的证明过程,从本质上认清楚勾股定理是直角三角形两直角边的平方和等于斜边的平方.
2 巧设题串,引导深度提问
学生是思维的主体,有效的问题串可以,激发学生主动参与,调动学生各层次的思维,进行探索问题、寻找解决问题的方法,让学生的思维处于良好的发展状态.一是老师问学生,二是启发学生问老师.前者是“提问”, 后者是“激问”,而“激问”又常常需要教师先用提问的方式去激活学生的思维.因此,教师的提问方法显得尤为重要,是调动学生的积极性和主动性的重要手段,是帮助学生理解概念,掌握知识,发展思维,提高能力的有效方法.
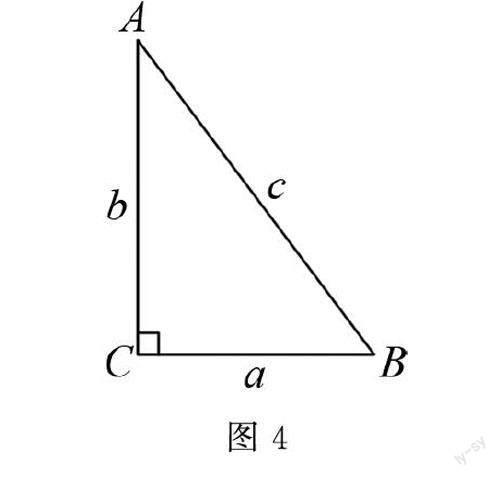
例1 已知△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=1,b=2,求c;
(2)若a=15,c=17,求b;
(3)若a=2m,b=5m,求c;
(4)若c=10,a∶b=3∶4,求a、b;
(5)若c-a=1, b=2, 求c.
讲解完第(1)题之后,老师可以尝试着让学生自己提出问题.
问1:刚才这个小题已知的是两条直角边,求斜边,你还可以提出什么问题?
生:已知一条直角边和一条斜边,求另一条直角边(给出第(2)题).
问2:刚才的题目都是具体的数字,我们还可以设置什么样的题目?
生:边可以用字母来表示(给出第(3)题).
问3:第(3)小题中,由a=2m,b=5m这个条件可以得到a与b之间有什么关系?
生:a与b的比是2:5.
问4:已知a与b的比可以求出c吗?
生:不能.
问5:如果需求出边的长度,该怎么办呢?
生:加条件.比如加a的长度.
师:太棒了,还可以加别的条件吗?
生:加b的长度或c的长度(给出第(4)题).
问6:两边之间的关系除了比例关系,我还可以换成什么关系?
生:已知两边和,两边差……(给出第(5)题)
通过问题串的形式,激发学生多层次思维的参与,一部分学生提出问题,一部分学生解决问题,调动学生各层次的思维进行探索问题,能够掌握并内化知识.讲解第(1)题的时候不是直接给出所有的小题,而是由6个问题串组成的,其中上一个问题都是引出下一个小题的铺垫,诱导思维层次较好的学生能自己提出问题并解决问题,这样,不仅理解了勾股定理的本质,并且进行了更深层次的灵活应用.如果学生提出问题的能力得到长期的培养,还能提升思维深度,变被动学习为主动学习.
3 层级提问,加强深度思维
在教学过程中,教师而应当引导学生,通过积极思维活动获取掌握知识的方法.教师需要精心设计提问,点燃学生的兴趣之火,启发与诱导学生发现问题解决的方式.特别是要解决一个比较难的问题,往往需要由浅入深,层层深入的设计问题,引发学生的深层思考,来达到难题的解决.
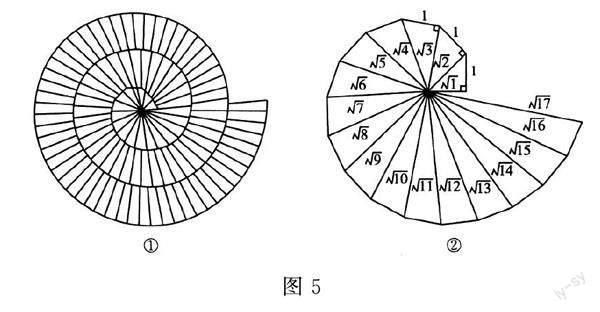
问1:你能用刻度尺和圆规在数轴上准确表示√13吗?回忆一下,之前有准确表示过吗?
生:借助正方形网格,利用面积法表示过.
问2:现在学习了勾股定理,有新的想法吗?
生:构造一个直角三角形,两直角边分别为2和3,斜边就是√13了.
问3:非常好,把√13分成两个数的平方和就解决问题了.你能在数轴上准确表示出√14吗?
大部分学生,使劲想着分成哪两个数的平方和,沉默了好一会儿,终于有同学举手了.
生:一条直角边是√13,另一条直角边是1,斜边就是√14了.(此刻有掌声响起来)
问4:太厉害了,能够跳出原来的思维.给我们打开了思路,谁还有想法?
生:两直角边分别是√5和3也可以. √10和2也可以.
问5:√15你会表示吗?……
生:可以通过两直角边分别是√14和1.
问6:是不是任何一个正整数的算术平方根都可以在数轴上准确地表示出来?
此时,学生会觉得自己成就感满满,竟然所有的正整数的算术平方根都可以在数轴上准确地表示,这是以前不敢想的事情,学生学习的热情高涨.通过这种层级提问的方式,进行深度的教学,不仅在于教“怎样做”,更教“怎样想”,完善学生处理问题的思维方式.
4 类比设问,培养发散思维
在教学中,把一个问题讲透,不但事半功倍,而且也更易看清这类问题的事物本质,使思维更深扎根. 课堂上,在探究勾股定理与面积关系时,笔者设计了以下几个问题引导学生.
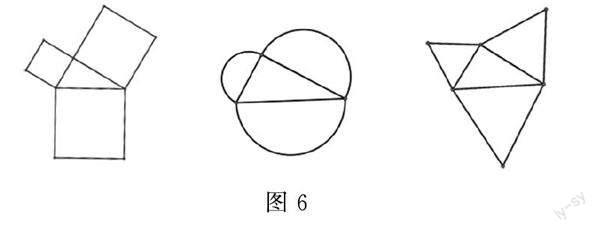
问1:如图6,以直角三角形的三边往外作三个正方形,你认为这三个正方形的面积有什么关系?
生:两直角边往外作的正方形面积和等于斜边往外作的正方形的面积.
问2:直角三角形的三边往外除了作正方形外,你觉得还可以往外作什么?
生:还可以作半圆、等边三角形、等腰直角三角形……
问3:你有什么发现?
生:发现,外侧图形形状变化,只要是同类图形,三个图形间的面积关系不变.
问4:三个图形的形状可以改变,你觉得还可以改变什么呢?
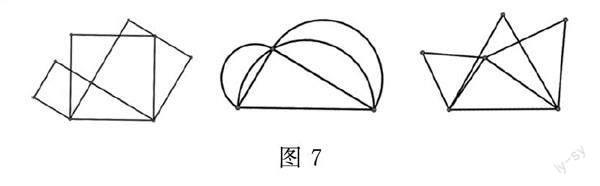
生:位置.如图7,可以试着斜边外侧的图形放到另一侧.
问5:相应的结论有变化吗?若有,怎样的变化?
有了刚才的一系列的探究,这道2019年宁波的中考题,学生很快就能找到几何法解决问题.
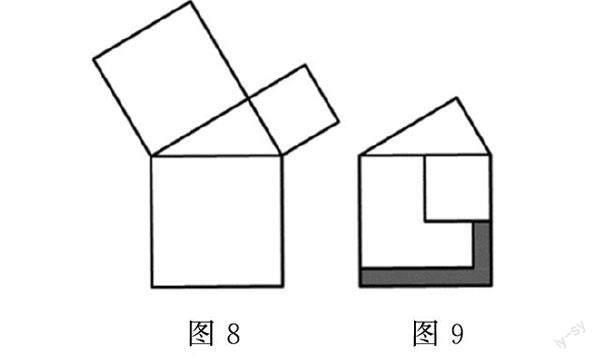
练习:(2019宁波)勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载.如图8,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图9的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
(A)直角三角形的面积.
(B)最大正方形的面积.
(C)较小两个正方形重叠部分的面积.
(D)最大正方形与直角三角形的面積和.
其实,解题训练,不在于量多,而在于讲透.在教学中,教师提供给学生充分思考和表达的时间,为学生搭建思考的“跳板”,暴露思维方式,从而引导学生突破表象深入思考,促进学生数学思维的深度及理解的宽度.
“授之以鱼,不如授之以渔”,在教学中如何进行有效的提问,深度的提问.当课堂提问成为我们关注与研究的焦点时,我们才发现,教师的认识与做法普遍存在问题:一是教师本身问题意识不够,有些教师认为“学生基础差,启发也白搭”.二是粗放提问,即不够精准,提问方向不明或范围太大,导致学生不知如何作答.三是教师提问的深度不够,有些问题思维要求低,甚至有些根本不需要思考,满足于表面的互动、热闹.四是教师提问的方式不多,习惯于老师提问学生作答,少见启发引导学生提问.笔者认为要有效的提问,教师首先要明确提问的目的;其次还要摸清学生的知识储备;然后寻找数学知识的生长点;同时关注数学思想与方法.具体设计问题时要注意把握好问题的难度、梯度、密度和角度.不仅要教师提问,还要引导学生能提出问题,使学生的主体地位和深度教学真正得到落实.
参考文献:
[1]丁桃红.数学课堂的提问要注意四度[J].中学数学教学参考(中旬),2017(3):69-70.
[2]刘光建.让问题在教学追问中自觉触发[J].中学数学教学参考(中旬),2020(4):18-20.
[3]乐意君.课堂提问中如何让“逻辑链”与“思维链”更加契合[J].中学数学杂志.2015(6)21-23.
