用秩1矩阵矫正法计算两类图的生成树数

2023-06-13雷玉娟杨维玲

厦门大学学报（自然科学版） 2023年3期

雷玉娟,杨维玲

(厦门大学数学科学学院,福建厦门 361005)

Kirchhoff矩阵树定理[1-2]给出了连通图的生成树数和Laplacian矩阵的代数余子式之间的关系[1],进一步,赋权的Kirchhoff矩阵树定理[1-2]给出了赋权连通图的生成树数与赋权Laplacian矩阵代数余子式之间的关系[1-2].然而一个矩阵的代数余子式并不容易计算, Klee等[3]利用Kirchhoff矩阵树定理和矩阵行列式引理,将Laplacian矩阵加上一个秩为1的矩阵,得到了新的矩阵行列式和生成树数之间的关系[3], 随后他们把这个结果扩展到赋权图上[4], 并计算出了一些特殊图的生成树数.

1 预备知识

首先回顾一些符号和定义.

本文所提到的图均指没有环、可以有平行边的无向有限图,对于图G,用V(G)和E(G)分别表示图G的点集和边集,|V(G)|和|E(G)|分别表示顶点数和边数.对于e∈E(G),G-e表示G删除边e得到的图,G/e表示G收缩边e、删除环后得到的图, 对于∀F⊆E(G),G/F表示G收缩掉F的边集、删除环后得到的图,这些表示在很多图论相关的书中都可查询到,比如参考文献[5].

对于简单赋权图(G;ω),这样定义函数ω:V(G)×V(G)→R,∀vi、vj∈V(G),若vivj∈E(G)且ω(vi,vj)=ω(vj,vi),定义ωi,j=ω(vi,vj)为图G中边vivj的权,若vivj∉E(G),则定义ωi,j=0.定义顶点vi∈V(G)的权值如下:

此时赋权图(G;ω)的赋权Laplacian矩阵L(G;ω)是一个V(G)×V(G)的对称阵,第i行、第j列的元素定义如下:

从上述定义易知,赋权的Laplacian矩阵是奇异的,因为这个矩阵的所有行加起来的和为0,然而它的代数余子式在计算赋权生成树数时有下面的表达式.

定理1(赋权的矩阵树定理)[1-2]令G是一个点集为V(G)={v1,v2,…,vn}、边权函数为ω的简单图,对任意的顶点vi、vj∈V(G),允许i=j,以下式成立:

(-1)i+jdet(L(G;ω)i,j),

(1)

由τ(G;ω)的定义可知,方程(1)的左边就是τ(G;ω),即为图(G;ω)的赋权生成树数. 对于没有环的无权(即边权视为1)图G,可以自然地将其视为赋权简单图,其中边的权值即为平行边的条数,例如图1(a)为有平行边的无权图K3,其对应的赋权简单图为图1(b).

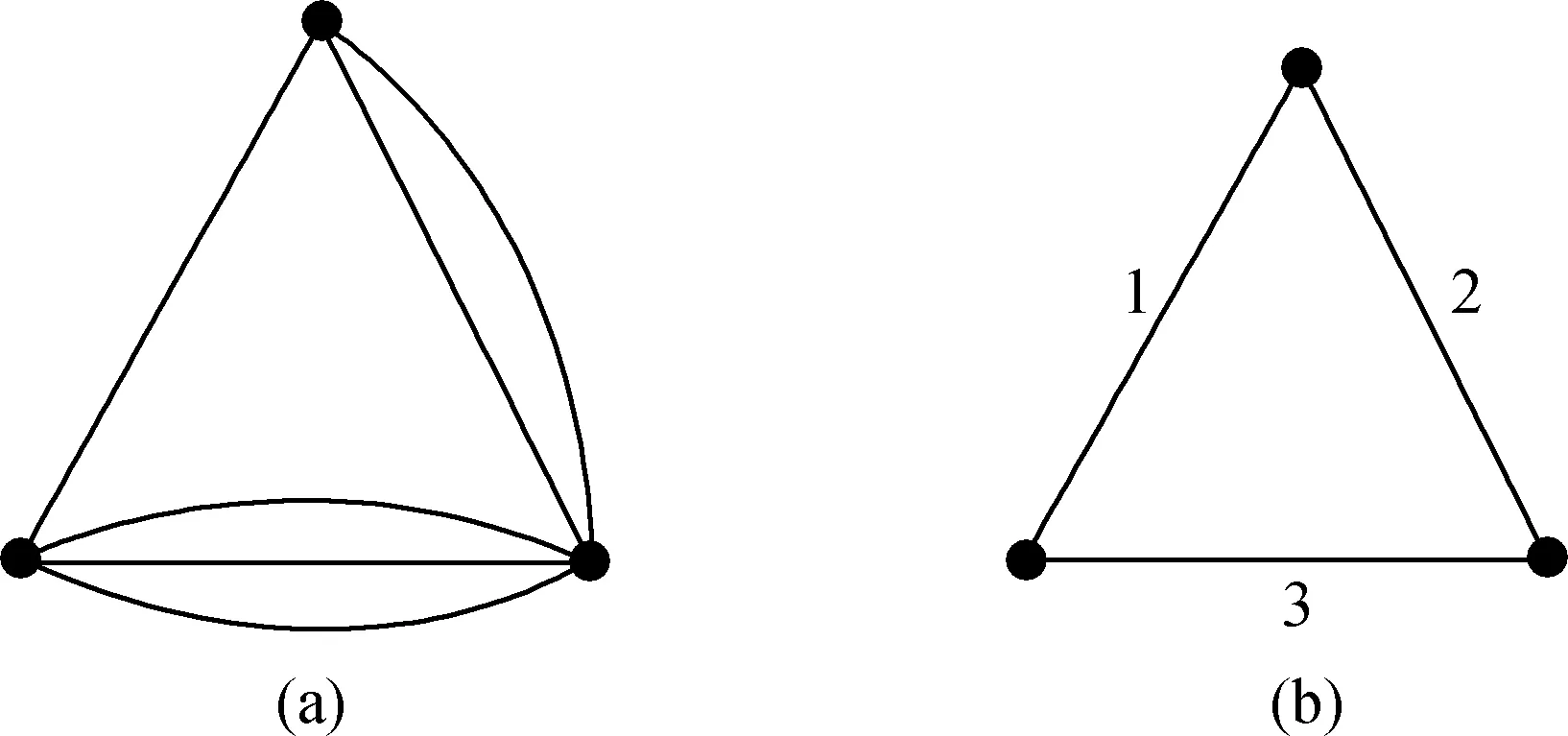
图1 有平行边的无权图K3(a)和其对应的赋权简单图(b)Fig.1 Unweighted graph K3 with multiple edges (a) and its corresponding weighted simple graph K3 (b)

赋权的矩阵树定理虽然给出了生成树数和det(L(G;ω)i,j)之间的关系,但是det(L(G;ω)i,j)一般不好计算. 因此将利用下面的矩阵行列式引理,记矩阵M的行列式为det(M),伴随矩阵为adj(M):

引理1(矩阵行列式引理)[6]令M是一个n阶方阵,令a和b是Rn中的列向量. 那么以下等式成立:

det(M+abT)=det(M)+bTadj(M)a,

特别地,若M可逆,有det(M+abT)=det(M)[1+bTadj(M)a].

在文献[6]中可以找到矩阵行列式引理的证明.

利用赋权的矩阵树定理和矩阵行列式引理,Klee等[4]得到了以下引理.

引理2[4]令G是点集为V(G)、边赋权为ω的图,L是G的赋权Laplacian矩阵,令a=(ai)vi∈V(G)和b=(bi)vi∈V(G)是RV(G)的列向量,那么以下式成立:

det(L+abT)=(∑vi∈V(G)ai)·

(∑vi∈V(G)bi)·τ(G;ω).

引理2的证明比较简单,可查询文献[4]中的引理1,其实这个引理是文献[3]中引理1的推广形式.

由矩阵的知识[3]可知,abT其实就是一个秩为1的矩阵,反过来,任何秩为1的矩阵,也可以写成abT.若det(L)不容易计算,通过取特殊的a和b,使得det(L+abT)的值比较容易计算,称方法为秩1矩阵矫正法.赋权的矩阵树定理虽然给出了生成树的计算公式,但是det(L(G;ω)i,j)通常不好计算.对于某些图,利用引理2,通过秩1矩阵矫正法,使其对应的行列式比较容易计算,进而得到其生成树数.用秩1矩阵矫正法,Klee等[3]得到了完全图、完全多部图、Ferrers图、threshold 图的生成树数的计算公式,进一步,Klee等[4]得出了对应赋权图的生成树数的计算公式.

在后面的证明过程中,还将多次用到以下引理.

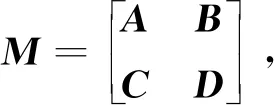
det(M)=det(D)·det(A-BD-1C).

2 几个定理

设Km,n是一个简单完全二部无权图,对任意的整数p≤min{m,n},记P是Km,n的维数p的匹配,运用引理2和3,就可以得到以下两个生成树数:τP(Km,n)和τ(Km,n-P).Ge等[7]运用电网络的相关知识得到了这些公式,本文利用秩1矩阵校正法给出这两个公式的简短的新证明.

记Km,n的二部划分点集分别为V1和V2,其中|V1|=m,|V2|=n.

定理2对Km,n任意边数为p的任意匹配P,可以得到

τP(Km,n)=(m+n)p-1(m+n-p)mn-p-1nm-p-1.

定理3Km,n-P表示图G删掉边数为p的匹配P后得到的图,可以得到

τ(Km,n-P)=(mn-m-n+p)(mn-

m-n)mn-p-1nm-p-1.

Zhang等[8]计算了τ(Kn,n-P)=(n2-2n+p)(n-2)p-1n2n-p-3,定理3是这个结果的推广.

3 定理的证明

记In表示n阶单位阵,1m,n为元素全为1的m×n阶矩阵,0m,n为元素全为0的m×n阶矩阵,1n为Rn中元素全为1的列向量,0n为Rn中元素全为0的列向量.首先说明一点,对于图G,若只是其顶点顺序的标号发生变化,则变化后的图仍与图G同构,而同构图的生成树数是相等的.即上述的几个定理的结果跟顶点的标号无关,这样就可以对顶点的顺序进行特殊的排列,得到所需的矩阵形式.