借助矩形模型图式探寻乘法运算的一致性

王燕珠

矩形模型图式有助于计数单位的认识，有助于贯连小学阶段的整数乘法、小数乘法和分数乘法。基于数的认识和数的运算的一致性，笔者通过整数、小数和分数的计数单位的整体认识，帮助学生形成和发展数感，并借助矩形模型图式探寻乘法运算的一致性，以加深学生对数学学习的整体感悟和一致性感知，发现数学的至简之美。

一、问题的提出

在一节小学数学分数乘分数的课堂教学里，面对“用面积模型表示3/4的1/4是多少”这个学习任务，一个学生突然很沮丧：“不是3/4的1/4吗？我也是把3/4再平均分成4份，可是这样画看不出结果是多少？”细看他画的图，原来他尝试把3/4的部分再次竖着平均分成了4份，两次均分都是竖着分，为什么不能直观看出结果呢？学生为什么坚持竖着两次均分呢？

是的，“3/4的部分再次竖着平均分成了4份”并不能直观看出原单位面积图形到底被平均分成了几份，可以把3/4看成300/400，300份就能被均分成4份了。学生坚持竖着两次均分主要是因为受习惯影响，在前面分数乘法的学习中，碰到的基本是单次均分，要么单次竖着均分，要么单次横着均分，都可直观看出结果。那么如何引导学生进一步认可“求3/4的1/4是多少，用乘法计算”？如何引导学生理解需要横向和纵向二維观察的面积模型表示分数乘法？

对于面积模型学生并不陌生，纵观北师大版小学数学教材，在整数乘法、小数乘法、分数乘法都有不少的涉及和使用，其他版本教材也基本如此。用面积模型表示分数乘分数时，需要横向和纵向的二维观察，按理说学生是不陌生的。那么问题在哪里呢？问题就出在“为什么要用面积模型？”显然不是“因为面积模型一目了然，很直观”就可以回答清楚的，必须弄明白面积模型使用的必要性。实际上，乘法运算本身，在计算3/4×1/4=3/16时产生了新的分数单位1/16，可借助面积模型直观得到。关于分数乘法里的面积模型，研究者刘加霞将其列为乘法的现实模型之一，称之为矩形模型。这里的矩形模型在整数乘法里实际上就是点阵图，在小数乘法和分数乘法里就是面积模型，所以基于对整数、小数、分数乘法运算的整体性理解，笔者将其称之为矩形模型，对应的图式就是矩形模型图式。另外，要充分认识数的运算的一致性，要清楚“数的认识的一致性”这个前提，基于数的认识和数的运算的一致性，笔者通过整数、小数和分数的计数单位的整体认识，帮助学生形成和发展数感，并借助矩形模型图式探寻乘法运算的一致性，以加深学生对数学学习的整体感悟和一致性感知，发现数学的至简之美。

二、借助矩形模型图示，探寻乘法运算的一致性

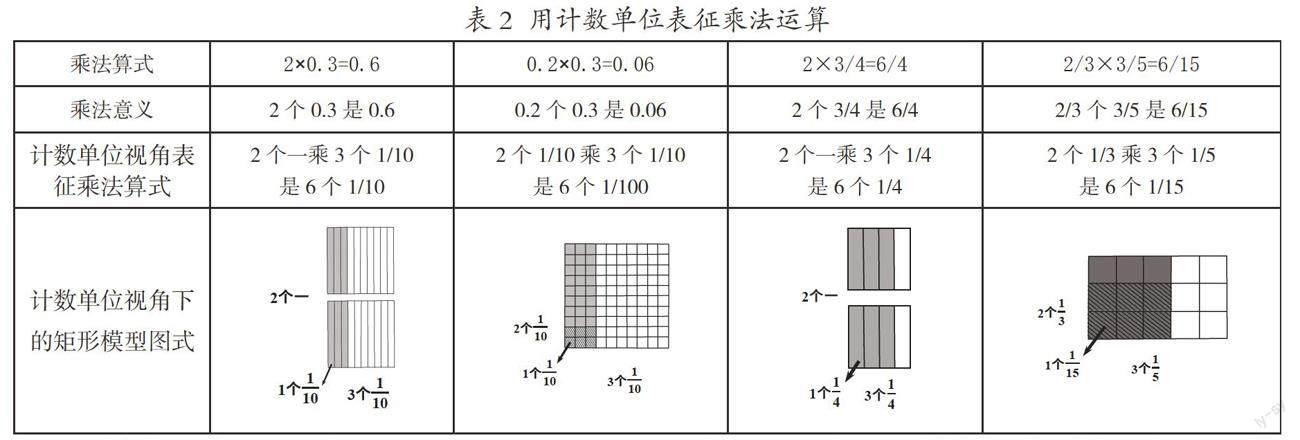
相比乘法现实意义的多样性，乘法算理更具一般性，算理承载着数和数运算的抽象发展，肩负着学生数感的形成，承担着促使学生运算能力提升的关键作用，所以，算理的探索是小学学习最重要的任务之一。如果能将乘法算理和乘法现实意义相联系，学生的发现问题、提出问题、分析问题和解决问题的能力也会随之发展和提升。基于乘法的现实意义，研究者刘加霞将乘法的现实模型概括为等量组的聚集模型、倍数模型、配对模型和矩形模型，并进一步指出最基本的是聚集模型，其他几种模型都可以转化为聚集模型。这里由于要借助矩形模型图来认识计数单位视角下的乘法运算，笔者尝试用等量组的聚集模型这个最基本的模型来认识乘法的意义，以沟通乘法算理与乘法意义之间的联系，进一步认识乘法运算的一致性，如表1、表2所示（用计数单位表征乘法运算）。

（一）整数乘法运算的一致性

以2×3=6、2×30=60、20×30=600这三种情形为例，用“往回看”的方法，先看整十乘整十的情况，最为熟知的一条规律就是“先不看乘数末尾的0，2和3相乘得6，乘数末尾共有几个0，就在6的后面添上几个0”，如果这样的规律发现仅通过几组乘法算式得到，而没有加以解释，那么就丧失了很多说理明理的数学学习机会。2个十乘3个十，得到了与20、30这两个乘数都不一样的计数单位“百”，乘法运算过程里诞生了新的计数单位，借助矩形模型的图式可以清楚地看到：横向观察是3个十，竖向观察是2个十，根据行列的排列规则，先看10行10列，十个十就是百，先有一个百，再依据排列（2排3列）的顺序，共能数出6个百。以此类推，借助千的立方体观察20×300，可以观察到10个100得1个千，共得到6个千，所以20×300=6000。

用同样的方法继续“往回看”2×30=60和2×3=6，根据排列顺序，分别共得6个十和6个一，也就是60和6。从自然数的角度看数感的形成和发展，有研究表明，人们普遍天生有个数方面的数感，容易察觉到几个一，而对于几十个几十，几十个几百等不是“一”的计数单位，就难以对结果有明确感知。行列的有序排列，也就是矩形模型图式，贯通了乘法和加法的联系，使人们可以在乘法的运算中，感受到数的不断累积，进一步形成和发展与较大计数单位有关的数感。

（二）小数乘法运算的一致性

以2×0.3=0.6、0.2×0.3=0.06为例来看小数乘法，2个0.3实际上就是2个3/10，观察矩形模型图式，横向看是2个一，竖向看是3个1/10，1个一先乘1个1/10得1个1/10，计数单位与乘数0.3的一样，再根据行列顺序数一数，共得6个1/10。算式0.2×0.3=0.06，2个0.1和3个0.1相乘为什么得到两位小数0.06呢？得数的计数单位与乘数0.2和0.3为什么都不一样呢？观察矩形模型图式，可以将0.2×0.3理解为0.2个0.3，即2/10个3/10，那么就要先关注1/10个1/10，也就是1/10的1/10，为1/100，1/10个1/10是1个1/100，得到了新的计数单位1/100，根据行列排列的顺序数一数可得6个1/100，为6个0.01，是0.06。

小数是基于现实生活度量的需要，由于度量需求的精准，需要十等分、再十等分、继续十等分等，它是一种更具现实意义的数。但是小数乘法算理仍是建立在分数乘法算理的基础上，且基本与分数乘法算理一致，由于小数是更具现实意义的一种数，要形成和发展关于小数的数感，必须通过分数的意义和分数乘法的算理来深刻认识小数和小数乘法最原本的模样，再结合小数丰富的现实意义，进一步发展与小数有关的数感和量感，完成对小数这一具有明显现实意义模型的进阶认识。

（三）分数乘法运算的一致性

分数的乘法运算是建立在分数的意义、分数单位、真分数和假分数等知识的基础上的，通过分数乘法运算进一步认识分数的意义，认识到分数与整数、小数一样都有明确的计数单位，分数的计数单位就是分数的分数单位，分数的乘法运算同整数乘法和小数乘法一样，是基于计数单位的累加，在算理上是一致的。算式2×3/4=6/4，表示2个3/4是6/4，即2个一乘3个1/4是6个1/4，观察矩形模型图示，1个一和1个1/4相乘，得1个1/4，乘积的计数单位和3/4一样，再根据行列的排列顺序，共6个1/4，得6/4，化成最简分数后是3/2。另外，根据分数的意义和倍数的知识储备，将3/4理解为一个倍率，一个数的几分之几是多少相当于求一个数的几倍是多少，都可以用乘法计算，对部分学生来说，这样的类比推理是有现实意义的，也是可以抽象理解的。但考虑到小学生身心发展的特点，抽象意识还有待萌芽和发展，那么如何使学生认可“一个数的几分之几是多少，用乘法计算”这一基本事实呢？实际上，根据画图操作，学生不难发现2的3/4是6个1/4，即6/4，2个3/4也就是6个1/4，也得6/4，因此从计数单位的视角观察操作过程和操作结果都能发现：2的3/4是多少，相当于求2个3/4是多少，再给学生提供多一些的具有现实意义的分数情境问题，在不断的独立思考、合作交流中进一步认识和发现其中的规律，促使学生不断认可“一个数的几分之几是多少，用乘法计算”这一基本事实。

求2/3的3/5是多少为什么用乘法列式？学生难以具象化認识其中的关联，借助矩形模型图示可以解决这一问题。根据分数的意义，“2/3的3/5是多少”也可做矩形模型图示，竖向看是2个1/3，横向看是3个1/5，先用行列排序的方式观察计数单位的情况，1/3个1/5就是1/15，用计数单位1/15来数一数，共有6个1/15，得6/15，化成最简分数后是2/5。从行列的观察角度还能进一步发现，矩形模型图示表示的也是2/3个3/5，列式为2/3×3/5。只从一个数的几分之几是多少来观察矩形模型图示，这里仍存在一个疑惑点：为什么2/3的3/5是多少，得数的计数单位是两个乘数的计数单位的乘积呢？学生如果只关注分数的意义，停留在不断思考“2/3的3/5是多少”这个问题本身，不但想不明白结果是多少，也难以想明白2/3的3/5为什么也用乘法计算。一般来说，求2/3的3/5是多少，其结果仍是相当于求2/3的3/5的部分占原单位“1”的几分之几，所以如果把思考的焦点聚集在原单位“1”被均分的情况，很快就能活络学习思路，用行列的观察方法来看待分数乘法，就能明白2/3×3/5=6/15像2×3=6一样，2个3是6，2个1/3乘3个1/5是6个1/15，即2/3个3/5是6个1/15，得6/15。

（四）乘法运算的一致性

上文分别根据整数、小数和分数的学习和对应的乘法运算学习脉络，借助矩形模型图示，用行列排序的观察方法呈现了乘法运算的一致性。回看矩形模型图示，可以进一步总结和发现乘法运算一致性主要体现在两个方面：第一，乘积的计数单位就是两个乘数的计数单位相乘。乘积的计数单位具体如何产生，要结合具体的图示，主要有两种情况，一是与其中一个乘数的计数单位一样，这类一般是其中一个乘数的计数单位是一，那么乘积的计数单位就与另一个乘数的计数单位一样；二是乘积的计数单位与两个乘数的计数单位都不一样，结合矩形模型图示的观察，顺着行列排序的顺序，先竖向看再横向看，或者先横向看再竖向看，如果观察得到十个十，会产生新的计数单位百，如果观察得到1/10个1/10，会产生新的计数单位1/100，以此类推。第二，无论是从乘法的意义出发，还是从乘法的算理出发，都能回归到“几个几”来进一步探究，因为乘法是加法的简便运算，乘积就是计数单位累加的结果。

三、结语

基于运算的整体性视角，乘法运算的一致性学习需要学生主动参与乘法运算算理探讨的过程，观察和明晰说理。教师要密切关注计数单位的学习，以计数单位的学习为抓手，重视矩形模型图式的应用，多用数理的方式展开乘法算理的学习，让学生能看到、能推理、能言说，提升学生对乘法运算的一致性认识和理解，助推学生数学核心素养的形成和发展。