以“核心问题”为驱动 让“先学后教”课堂更精彩

丘文君

摘要：核心问题是课堂深度研究的动力所在，在“先学后教”理念的影响下，数学教师需提前让学生思考了解数学知识，自主学习，从而为课堂教学深度研究奠定基础。教师要以“核心问题”为研究点，在生成“核心问题”上主动探究一些，在立足“核心问题”上高位一些，在聚焦“核心问题”上精准一些，在关联“核心问题”上丰厚一些，在拓展“核心问题”上深刻一些，使不同的学习环节有不同的侧重点，做到“先学后教”，让数学课堂教学更加高效。

关键词：小学数学；核心问题；先学后教；高效课堂

中图分类号：G623.5文献标志码：A文章编号：1008-3561（2023）15-0093-04

问题是数学的心脏，是学习数学的动力。郑毓信教授认为，教学中的“核心问题”不仅要包括“知识性问题”和“思维性问题”，还要起到“引领”与“驱动”的双重作用。可见“核心问题”是源自生本的问题，其涵盖教学重难点，指向数学知识本质，启发学生学习思维，促进学生有效探究。“核心问题”可以是一个或几个。基于“核心问题”展开的“先学后教”课堂教学，倡导教师以学定教，从“学”的视角出发，确立好教学中的“核心问题”，引领学生主动探究，从而有效撬动学生思维，让学生掌握知识技能，领悟思想方法，将教学活动引向深入。那么如何以“核心问题”为驱动，让“先学后教”课堂变得高效、走向深入呢？本文将从以下方面进行探讨。

一、生成“核心问题”，让“先学后教”探究主动一些

生本问题是课堂的“真问题”，是以学生为本、从学生出发的真问题，或是由学生自我发现和提出的真问题。“先学后教”课堂教学，顺学而导，注重对生本问题进行甄别、加工与提炼，生成课堂教学“核心问题”，让学生在问题引导下，在同伴合作与师生互动中，积极思考、主动探究，获得技能，发展素养。

例如，“百分数的认识”教学可这样开展：课前，教师根据学习内容下发预习导学单，让学生寻找学习材料；课中，让学生动手写一写、读一读。在学生对百分数有初步感知的基础上，教师进行提问：“会读会写之后，你们还有什么疑惑？”引发学生自主提出问题，如“百分数是什么”“百分数有什么用”“百分数与什么有关系”“百分数和分数有什么不同”“为什么要有百分数”等这些看似复杂纷乱的学习问题。此时，教师对学生提出的问题不是简单地提一个就解决一个，而是对问题进行精选归类，整理提炼出要重点解决的问题：什么是百分数？百分数有什么用？百分数与分数有什么区别？接下来，整节课就围绕这3个“核心问题”，以问促疑、以问带学、以问引思，把“做”的过程留给学生，让学生变被动学习为主动学习，变零散的知识学习为系统性学习，从而对百分数的意义有更加透彻的理解。“先学后教”课堂教学，要注重“核心问题”的生成，只有学生有了问题意识，带着问题去思考，其探究才是主动的、有效的。

二、立足“核心问题”，让“先学后教”目标高位一些

根据认知心理学的相关理论，目标驱动在学习者的知识习得过程中发挥着重要作用。“先学后教”课堂教学，学习目标要有挑战性，以激发学生的学习欲望。为此，学习目标的确立要立足知识本质，立足“核心问题”，把引发学生思考、提升学生数学学习能力作为重点。

例如，在“折线统计图”教学中，从以往的教学经验来看，学生对读图、画图没有什么问题，教学的难点在于如何有效理解折线统计图的特点。为此，教师应立足知识本质，设计核心问题，诸如“从折线统计图上的点，你看出了什么”“从折线统计图上的线，你又看出了什么”“联系折线统计图的标题信息，你猜猜变化的原因可能是什么”。在这些核心问题中，教师可通过课堂情境图和具体教学中的统计图，引导学生观察、比较、分析、交流，有效解答：借助折线统计图的点，可以明显地看出数量的多少；借助折线统计图的线，可以看出数量的增减变化、整体的变化趋势，从而进行合理的判断和预测；注重结合生活实际寻找数据背后的原因，体会统计的实际应用价值。在这样的学习过程中，“核心问题”的导向明顯，在揭示知识的本质的同时，把学生的思维引向深入。

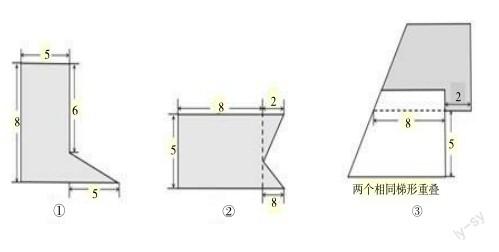
又如，在“梯形的面积计算”教学中，教师可利用转化思想进行梯形面积公式的推导，体现解决问题策略的多样化。具体而言，教师可设计以下问题：你能把梯形转化成我们学过的图形吗？新图形的边与梯形的边、新图形的面积与梯形面积分别有什么关系？梯形面积公式是什么？同一个梯形，我们用不同的方式推导出同样的公式，这些推导方式之间有什么联系？让学生围绕问题展开研究。学生借助学习经验，迁移应用分、合、移、补等方法，把梯形转化成学过的图形，探索梯形的面积计算公式。学生也可以开展小组合作学习，自主选择探究方法，并进行交流，介绍推导方法。教师要对学生的探究过程进行梳理，把9种梯形面积公式的推导方法有所侧重地呈现出来（如下图）。

教师引导学生通过对比分析、思考交流后得出：无论是“倍拼”“剪拼”还是“分、合、移、补”，其目的都是“将未知转化为已知”。设置这样的“核心问题”，能灵活应用转化思想、对应思想，不但能推导出梯形的面积计算公式，还触发了学生的深度思考和创造。可见，“先学后教”课堂教学，不应仅仅把学习目标定位于知识技能，还应该站得更高一些，引领学生看到知识背后所蕴含的方法与关联。

三、聚焦“核心问题”，让“先学后教”内容精准一些

受教材和所学内容的限制，课堂教学存在零碎化、片段化的现象。“先学后教”课堂教学，倡导对学习内容的优化，整合成“核心问题”实现精准施教。这既能引发学生的认知冲突，激发学生的探究欲望，让学生主动参与到问题的解决中来，还能有效构建起直指学习本质、关联整体知识的课堂。为了更好地说明教学的准确情况，下面将列举一个案例。

先看一堂课的数据统计：教师讲授1分钟，占课堂时间的2.5%；学生独立思考7分钟，占课堂时间的17.5%；学生小组合作9分36秒，约占课堂时间的24%；剩下的是学生之间的交流对话时间，共22分24秒，占56%。教师只讲了1分钟的话，是不是感觉不可思议呢？这堂课是来自福建省宁德市福安师范学校附属小学的林琳老师执教的“组合图形的面积”一课，这节课教学用3个问题串联起“学”“习”“思”的环节。

教学环节一，以教材例4房子侧面墙的形状为研究对象，提出问题：“你准备用什么方法求出下面这个组合图形的面积？请说说你的想法。”这个问题设计巧妙之处在于只给图形而没提供数据。教师的设计意图很明确，先寻找、确定问题解决的方法，锻炼学生思维能力，不急于得到结果。学生在解决问题的过程中，不仅进行了个性化的思考，还在同伴互助、合作交流、倾听表达中，经历了思维的碰撞，收获了解决问题的方法，体会到转化的数学思想。

教学环节二，教师侧重对学生思维能力的培养，提出以下问题：这道算式能求出下面涂色图形的面积吗？请说说其中的道理。教师提供1个算式（8×5+5×2÷2），3个图形（如下图），这3个不同形状的图形融合了“割补、平移、旋转、对称、等量代换”等具体的“转化”方法，3个不同形状的组合图形面积均可由同一算式计算，在对比分析中促使学生的思维螺旋上升。

教学环节三，基于大观念的导引，以问题“求组合图形面积的方法和学过的推导平面图形面积的方法一样吗？为什么”有效地促使学生把学习平行四边形、三角形、梯形的面积推导过程的新知探究和组合图形面積的综合运用建立联系，引导学生回顾平面图形面积由度量法简化为计算法，感知由未知变换为已知的“思维进化”历程。

在上面三个“学”“习”“思”的环节中，林琳老师的整堂课聚焦“核心问题”，以问题驱动学生独立思考、合作探究、交流对话、互动成长，不但实现了知识、技能、能力目标的达成，而且促成了学生的精彩展现、思维的高质绽放。同样，在“圆的整理和复习”一课教学中，教师不妨围绕确定好的两个核心问题“如何整理能清楚表达知识之间的联系？你有哪些易错点，怎样弄明白”串联起全课，引领学生从浅层的知识复习转变为高阶的关系梳理，从被动地等教师分析错题转变为自主整理错题并反思错因，进而培养学生的深度学习与反思能力。由此看来，在“先学后教”课堂教学中，教师只要搭建足够巧妙的问题支架，呈现精准优化的学习内容，就能驱动学生真思考、真学习。

四、关联“核心问题”，让“先学后教”练习丰厚一些

郑毓信教授指出，练习的问题，不求全，而在联。在数学“先学后教”课堂教学中，教师应注重依托“核心问题”建立起知识间的联系，实现知识的迁移与应用，通过变式化、连续化、题组化的课堂练习设计，巩固和强化学生的学习能力。例如，在“比例的单元练习”中，教师可选用与生活实际相关联的素材编成这样的问题组。

问题1，学校长方形操场的长是60米，宽是40米。明明沿着操场的四周跑步，小艺把他跑不同圈数的情况画成统计图。哪一条线能描述明明的跑步情况？我的想法是。”

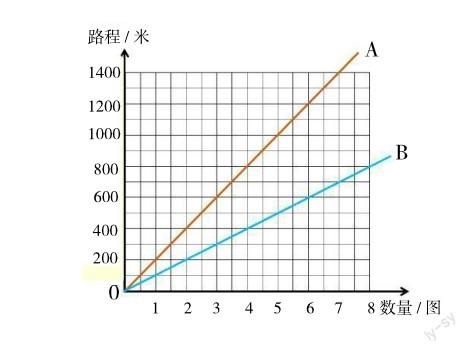
这道题是综合基础题，通过阅读素材获取数据，先求出长方形操场一周长度为：（60+40）×2=200（米），再利用题目中跑一圈的路程所需的两个要素总路程和圈数，可算出A条线跑一圈1400÷7=200（米），B条线跑一圈800÷8=100（米），对比可知，A条线能正确描述。

问题2，明明在操场上跑了2300米，一共跑了多少圈？你能用比例的知识解决吗？此题是一道应用题，可以迁移运用前一道题的经验，应用比例知识，结合问题情境进行圈数的运算。学生先假设一共跑了x圈，再依据总路程∶圈数=每一圈的长度（一定），列出比例式：2300∶x=200∶1，求出x=11.5，也可以列出比例式：2300∶x=1400∶7，求出x=11.5。

问题3，采用对话式呈现，明明说：“把学校操场画在了纸上（长方形图，长10厘米，宽8厘米）”，小艺问：“明明画的长方形的长和宽与操场实际的长和宽成比例吗？说说你的理由。”作为一道说理题，方法是多样的，可以求出比值进行比较判断，也可以化简进行比较判断，还可以利用比例知识，列出比例式求出对应的长和宽，再与实际操场的长和宽进行比较。

问题4，怎样调整这个长方形的长和宽，才能与操场实际的长和宽成比例？我的调整方法是。这道题的设置，既有开放性，又突出了数学知识的现实应用情境，需要学生进行思考分析后，再作出调整。

练习题组的设计与应用，能查缺补漏，达成对知识更高层次的理解，巩固和提升学生的知识掌握和应用能力。

五、拓展“核心问题”，让“先学后教”经验深刻一些

“先学后教”课堂教学，提倡把握教材重难点、厘清课堂学路、确定教学思路的有机融合，利用“核心问题”拓展思维的深度，让学生对数学知识本质的理解透彻一些。

例如，在“综合应用百分数知识解决问题”教学中，教材呈现的问题是：某种商品4月末的价格比3月末下降了20%，5月末的价格比4月末又上涨了20%。5月末的价格和3月末相比是上涨了还是下降了？变化幅度是多少？学生迁移利用之前“分数除法”的经验，先借助线段图，直观呈现数量关系，找准量率之间的关系，然后通过不同数据进行计算验证，想出多种解决问题的方法：可以把3月的价格假设为100元这样具体的量，也可以设为抽象的单位“1”，还可以用字母表示，都能得出“5月比3月降了4%”这个结论。

有了结论，是不是研究就结束了呢？若是换一个情境去研究，又不具有挑战性。怎么办？此时，教师可以这个结论为学习生长点，引出新的问题：刚才我们研究了先下降20%，再上涨20%，结果是下降4%，那要是先上涨20%，再下降20%，结果又会怎样呢？学生通过具体计算发现，无论是先降后涨，还是先涨后降，最终结果都一样。这时，教师再提出下一个问题：为什么先降后涨与先涨后降，结果都一样呢？引导学生对比两个算式，从中发现其中的规律：原来是这两个带括号的因数交换了位置，根据乘法交换律，可以知道得数是不变的，所以无论是先涨后降，还是先降后涨，结果都一样。数学学习需要进行理性分析，通过逻辑化的计算，得出其中的数学关系，从而有效判断最终结论，这是数学学习所追求的目标。因此，在“先学后教”课堂教学中，教师需要适时拓展深化“核心问题”，引导学生挖掘问题解决背后的奥秘，从中体会到数学知识之间的关联，搭建起数学学习的整体结构，让学生学习经验更深刻一些，让课堂推进更深入一些。

综上所述，“核心问题”驱动下的“先学后教”课堂教学，能有效整合生本问题，凸显数学本质，优化学习内容，关联知识应用，拓宽思维层次，促进学生在探究合作学习中实现对知识、技能、目标的达成，使得学生在思辨修正反思中理解数学知识的内涵和外延。“核心问题”驱动下的“先学后教”课堂教学，能让学生形成积极的成长体验和正确的价值观，并实现生生、師生的深度对话、和谐相长，从而让学生的学习真正发生，让教学真正高效。

参考文献：

[1]杨芳.问题引领课堂促进深度学习———小学数学提炼核心问题的课例研究[J].天津教育，2022（36）.

[2]陈东虎.小学数学开展先学后教教学活动的实践策略[J].天津教育，2022（31）.

[3]潘瑶瑶.先学后教：重建自主探究型课堂的教学范式[J].教书育人， 2022（23）.

[4]李云锦，林运来.指向核心素养的“问题解决”教学实践[J].数学通讯，2022（02）.

Driven by "Core Issues" and Making "Learning Before Teaching" Classroom More Exciting

Qiu Wenjun

（Shanghang County No.2 Experimental Primary School， Fujian Province， Shanghang 364200， China）

Abstract： The core issue is the motivation for in-depth classroom research. Under the influence of the concept of "learning before teaching"， mathematics teachers need to let students think about teaching knowledge in advance and learn independently， thereby laying the foundation for in-depth classroom teaching research. Teachers should take the "core issues" as the research point， actively explore some of the "core issues" in generating them， focus more on the "core issues"， focus more accurately on the"core issues"， enrich some of the "core issues"， expand the "core issues" deeply， make different learning links have different focus， achieve "learning before teaching"， and make math classroom teaching more efficient.

Key words： primaryschoolmathematics； coreissues；learningbeforeteaching； efficientclassroom