立足结构化教学优化题组设计

陈明珠

数学知识是有结构的，数学教学也是有结构的，实现教学结构化，可以助力学生知识、方法和思维的有效建构，结合教学实践，教师立足结构化教学，从这四个方面优化题组设计：固点（理解知识点的本质）、串线（大单元整合成一条清晰的知识线）、组面（单元与单元延伸成知识模块）、成体（构建小学生的知识结构体系），将学生的知识结构体系进行优化，培养学生拥有一个完整的结构化思维，达到培养学生数学核心素养的教学目标。

认知心理学家布鲁纳曾经说过一句话：“已经掌握的知识，如果没有经过结构进行完美的联系，随着时间的推移就会变成被人所遗忘的知识。”小学数学结构化教学，是指教师站在系统的高度，从整体的角度出发，针对学习的发生以及过程进行审视，以此来对学生的结构思维进行培养，形成“带的走”的学习方法和能力。“题组”能够做到的就是将内容、形式、思维方法、解法相似的题目结合在一起组成一个组题。笔者通过实践发现只要立足结构化教学，从固点、串线、组面、成体这四个方面优化题组设计，就可以优化和完善学生的知识结构体系，推动学生结构化思维的飞速发展，进而达到提高学生数学核心素养的教学目的。

一、立足结构化教学的生长点 ，优化“固点”题组设计

新课标指出，数学的结构化教学是一个整体，它的生长点指的是每个“碎片化”的单一的知识点，而“固点”就是在每一章节的学习、小结中，结合教材的知识点，从多角度、多方面，针对概念、意义以及知识点进行深入了解，并进行分析和总结。要透彻理解知识点的本质，而不仅仅停留在知识的表面。只有巩固好每个知识点，才能进行知识间的沟通和关联，这样结构化教学才有生长的力量，因此我们要立足结构化教学的生长点 ，优化“固点”题组设计。牢牢地掌握知识点，为学生学习数学知识打下坚实的基石，从而进一步提高学生的学习质量以及学习能力。

例如，教师进行“圆柱的表面积”这一节课的结构化教学时，侧面积公式就是结构化教学的生长点，只有扎实的掌握了侧面积公式，才能灵活解决有关于圆柱表面积的实际问题，做好知识间的沟通和串联，因此笔者设计了以下的“固点”题组，力求让学生深刻理解并掌握圆柱的侧面积就是底面周长×高。

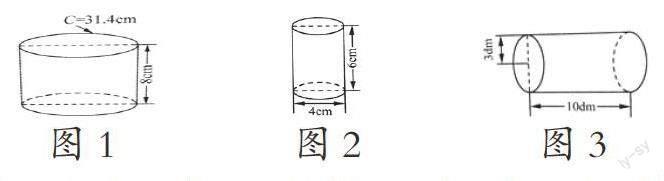
固点题组：求以下圆柱的侧面积。

第一题是已知底面周长和高，求圆柱的侧面积（如图1），第二题是已知直径和高，求圆柱的侧面积（如图2），第三题是已知半径和高，求圆柱的侧面积（如图3）。它们内在联系为图2将圆的直径转化为圆底面周长，图3将圆的半径转化为直径，再转化为底面周长，从而求圆柱的侧面积。

通过以上练习，厘清 “已知圆柱的半径、直径、底面周长，求圆柱的侧面积”三种题型之间的内在联系。都是要把它转化成底面周长，通过底面周长×高，求出侧面积。学生就在脑海里的认知结构中存入了“已知底面周长和高求圆柱的侧面积”这个固点，像这样抓住概念本质，优化“固点”題组的设计，有利于学生及时巩固理解知识本质，触类旁通，举一反三。因此，在教学每一节新课时，都要牢牢抓住该章节的生长点，优化“固点”题组设计，领悟知识的本质，扎实的掌握生长点，提高学习效率，优化学生的认知结构。

二、立足结构化教学的整合点，优化“串线”题组设计

结构化教学的核心就是整合，将知识点与知识点沟通、串联起来，用结构化的思维对单元知识、方法、思维进行整合，指导学生从碎片的学习到整体的学习，整体性越强、概括性越强，就越有利于学习的保持和迁移。因此在整合时不能仅仅是简单知识点的罗列，而是要优化“串线”题组设计，所谓的“串线”题组就是从单元整体的视角，将零散的知识点放到整个单元知识的结构当中，引导学生整理清楚知识脉络。有助于学生厘清单元各知识间的内在联系，纵向整合成一条系统的、明确的知识线，为结构化教学整合提供保障，从而构建学生新的认知结构，实现思维的拔节、提升。

例如，在“圆柱和圆锥”这一单元的结构化教学中，包含的知识有圆柱的特征、表面积和体积，圆锥的特征和体积等比较碎片的知识点，因此笔者立足“线”的构建，系统地将这些知识进行整合，优化设计了以下的“串线”题组：

一做。用一张长30㎝，宽20㎝的长方形纸叠出了一个圆柱。想一想，圆柱与长方形各部分之间有什么联系？什么变了？什么没变？

二思。制作无盖圆柱体形状的水桶需要多少铁皮是求什么？

三算。一个圆柱体的底面半径为2㎝，高为8㎝，它的表面积为多少？

四切。①把底面直径为20㎝，高为8㎝的蛋糕从沿底面垂直切成2半，什么变了，什么没变？如果沿底面垂直切成N半呢？②把底面直径为20㎝，高为8㎝的蛋糕平行于切成2段圆柱，什么变了，什么没变？那如果平行于底面切成N段呢？

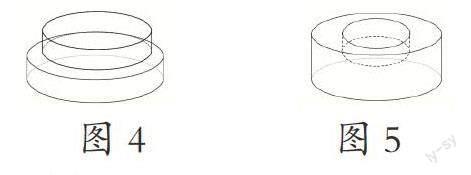
五涂。同学们如果要在这个双层蛋糕的表面部分（如图4），涂上一层厚厚的奶油，但是下底面不涂，你们知道涂奶油部分的面积是多少吗？

六挖。为了做造型，陈老师在这个直径为20㎝，高8㎝蛋糕里挖了一个直径为10㎝，高2㎝的圆柱（如图5），需要涂奶油（底面不涂）的面积是多少㎝2？

七伸。为了做造型，从棱长为10㎝的蛋糕中挖走了一个直径为3㎝，高为6㎝的圆柱，剩下的蛋糕是多少m3？

八变。一块圆柱形的橡皮泥，底面积是12㎝2，高是5㎝，如果把它捏成等底的圆锥，这个圆锥的高是（    ），如果把它捏成等高的圆锥，这个圆锥的底面积是（    ）。通过做（复习圆柱的特征及由来），思（复习表面积的概念），算（数形结合复习表面积两种计算公式），切（复习表面积的变化），通过涂和挖（复习整体求表面积的方法，并对比发现不管是涂N层还是挖N层都是求一个大的圆加几个侧面积），再通过伸（拓展了圆柱的体积），最后通过变（复习圆锥的体积）等一系列的练习将碎片化知识进行整合，以知识的由来、运用、拓展的顺序为线，串成一条完整的单元知识链，像这样优化“串线”题组的设计，使学生对“圆柱和圆锥”这一单元知识的认识从零散到条理，从模糊到清晰，从清晰到深刻，便于学生更深层次理解知识脉络，掌握学习方法，积累学习经验，从而建构了新的认知结构，因此在教学单元知识完后，教师要立足结构化教学的整合点，抓住本单元的核心知识点，优化设计一系列的“串线”题组，将知识点由点延伸成线，让学生触到知识的本质，从而提高学生的学习效率，进一步打开学生的眼界和思路。

三、立足结构化教学的联结点，优化“组面”题组设计

结构化教学强调联结点即教师要深入研读教材，挖掘单元与单元之间相关知识、方法、思维等内在关联和异同之处，并将其联结起来，从而展开结构化、科学化、系统化的教学，加深学生对知识含义的掌握，构建一个属于自己的数学网络图，同时也培养了学生认真仔细的观察能力以及自由发挥的想象力，有效提高了学习效率。因此我们可以立足结构化教学的联结点，优化“组面”题组设计，所谓的“组面”题组即打破常规单元内的知识梳理，找到联结点重组关联，将分散在各单元有联系的、相关的，本质是一样的知识点，通过对比、联想、归纳等方法进行横向整合，形成“知识面”。这样的“面”相较于“线”，更能让学生理清知识盲点，触及知识的本质，使知识更加系统化，从而完成模块知识的构建，为结构化教学的实施搭建了有力的桥梁，实现学生认知的升华。

例如，分数乘法、分数除法、比和百分数的应用题，他们零散的分布在六年级上册，但知识联系密切，他们的联结点是本质一样，都是分数乘除法应用题，用的线段图也一样。因此笔者优化设计了如下的“组面”题组：

一编。你们能根据下面的线段图编一道乘除法应用题吗？（如图6）

二解。①一条路长1000米，工程队已修了全长的1/4，还剩多少米没修？②一瓶牛奶，喝了300毫升，已经喝了1/4，这瓶牛奶一共多少毫升？③一本书有100页，看了和未看的比是1∶3，看了多少页？④一条泳道已经游了100米，是全长的25%，全长是多少米？

三比。比一比，这些题目有什么共同点，把你的发现写下来。

一编：先让学生根据线段自主编题，引导学生使用数形结合来理解知识的本质；二解：通过对学生编的不同题目进行分类整理，比如第一类是分数乘法，单位“1”已知，量和率不对应，第二类是分数除法，单位“1”未知，量和率对应，第三类是比的应用题，但是比可以转化成分率，单位“1”已知，量和率也对应，第四类是百分数的应用题，也可以转化成分率，也是单位“1”已知，量和率对应的问题。三比：学生通过自己分析，沟通联系，得出分数、比、百分数应用题，他们都是分数乘除法应用题。当单位“1”已知时，用单位“1”×对应分率＝对应量，当单位“1”未知时，对应量÷对应分率＝单位“1”。这样从“线”联结成“面”，既复习了旧知，也形成了新的知识网，建构了新的数学模型，有助于数学方法的运用、数学思想的产生，因此，在教学中可以立足于结构化教学的联结点，优化“组面”题组设计，注重單元知识之间的联系，抓住联系设计“组面”题组，对单元与单元的知识进行分析、比较、归纳、总结，实现练一组题，通一类题，从而“把书越读越薄”，数学思维更加深刻。

四、立足结构化教学的落脚点，优化“成体”题组

结构化教学的落脚点是帮助学生形成结构化的知识与技能和结构化的思想与方法。《义务教育数学课程标准（2022 年版）》针对数学基础知识的教学明确提出，教师要对数学课本进行熟练的掌握，不管是什么学段的学生都要有对课本局部的理解，同时，对整个小学阶段的数学课本要有全面的掌握，从而构建一个整体的结构化教学，有助于学生构建属于自己的知识网络。因此可以立足结构化教学的落脚点，优化“成体”题组设计，所谓“成体”题组是将知识点放到每个学段，乃至整个小学数学体系的知识结构上，从整体上把握知识结构设计题组，了解知识的产生和发展以及知识背后蕴藏的思维和内涵，从点—线—面—体感受知识之间的关联性，最终将知识与技能、思想与方法融为一体，从而实现结构化教学，完善学生的认知结构，形成结构化、一体化、系统化的知识体系。

例如，在结构化教学“长方体、正方体、圆柱和圆锥等立体图形的表面积和体积”时，其落脚点是沟通这些立体图形的表面积和体积之间的联系，统一成同一个计算方法，促使学生对立体图形的认识进一步系统化、一体化，因此笔者设计如下“成体”题组：

1.基础题：你能完成下面的表格吗？

2.综合题：你能自己探究出正三棱柱、正五棱柱等的表面积和体积吗？

以上题组涵盖了长方体、正方体、圆柱、圆锥、三棱柱、五棱柱等的表面积和体积。首先通过对长方体、圆柱等已学的表面积和体积公式的梳理，激发学生的原有经验，通过综合题拓展探究正三棱柱、正五棱柱等的表面积和体积，从而通过观察、对比、分析等构建小学阶段完整的立体图形表面积和体积的知识体系，发现所有直柱体的侧面积都是“底面周长×高”（图7），表面积都是“侧面积＋两个底的面积”，体积都是“底面积×高”图8，让学生对立体图形进行系统化的认识，了解知识与知识之间存在的关系，丰富完善学生的认知结构。

小学的知识具有“螺旋上升”的特点，每一年所学的新内容，都是前面基础的深化，越来越复杂、越来越抽象，从而形成完整的知识体系。实践也证明，学生大脑比较容易记住的是一定范围内各种关系、框架和体系，因此，我们可以立足结构化教学的落脚点，优化“成体”题组，将知识点放进学段里甚至整个小学阶段，做到心中装绿洲、眼中看森林，助力学生逐步构建每个知识体系，对知识形成整体的结构化认知，促进结构化教学。

五、结语

总之，我们要在结构化教学的基础上，寻找知识与知识之间存在的联系，优化设计“固点→串线→组面→成体”的题组，将碎片化的知识连成线、结成网、筑成块、构成体，不断对知识进行系统的总结、消化、提炼、升华，有助于学生学习能力的大幅度提升，以及将知识点、学习方法和思维方式进行结构化建构，推动学生结构化思维的发展，进一步提高学生的数学核心素养。