摩擦对引信后坐保险件解除保险特性的影响
2023-05-31邹陈来王雨时王光宇
邹陈来, 王雨时, 王光宇
(南京理工大学 机械工程学院, 江苏 南京 210094)
0 引言
后坐保险机构是利用弹丸发射时的后坐过载使保险件解除保险的一种引信常用保险机构,其设计需同时满足发射时可靠解除保险和勤务处理安全的要求。勤务处理安全性主要是保证引信意外跌落时不能解除对被保险件的保险。引信保险机构的作用可靠性要求与勤务处理安全性要求的区别:可靠作用即要求在一定发射过载作用下可靠解除保险,而勤务处理安全性则要求在规定(可信)的勤务处理过程中不能解除保险,主要是在意外跌落过载作用下不能解除保险。对于保险机构设计而言,两者是相互矛盾的。一般而言,提高作用可靠性将降低勤务处理安全性,而提高勤务处理安全性往往会降低发射时的作用可靠性。如何有效权衡安全性与作用可靠性之间的矛盾,合理选取机构的参数,是设计后坐保险机构的核心工作。文献[1-2]运用刚体动力学理论,分析了引信后坐保险机构斜置设计方案在勤务处理和发射时的动态特性。文献[3]运用刚体动力学理论和仿真软件ADAMS,对比分析了引信经典弹性后坐保险机构和刚性后坐保险机构对不同后坐过载作用时间的响应特性。文献[4]通过求解引信后坐质量-弹簧系统运动微分方程,结合ADAMS软件仿真,从工程设计角度提出:适当减小后坐质量,增大弹簧装配预压量、弹簧刚度系数以及将保险球导向孔轴线与引信轴线夹角取为45°都有助于解决引信后坐质量-弹簧系统保险与解除保险之间的矛盾。文献[5]根据实测的跌落冲击响应曲线,对引信后坐保险机构以不同落高、45°倾斜跌向不同介质时的可靠性进行了数值仿真。
文献[6-7]用分段求解运动耦合微分方程的方法得出了双自由度后坐保险机构的位移响应。文献[8]运用数值仿真方法研究了引信双自由度后坐保险机构发射、垂直跌落和倾斜跌落时的运动特性,解决了跌落安全性不足的问题。文献[9]结合控制理论和振动理论,得到了引信双自由度保险机构动力学方程和运动学微分方程,并分析了其振动特性。文献[10]对一种火箭增程弹用引信双自由度后坐保险机构的动态特性进行了仿真,并采用正交模拟得到了机构参数的最优解。
文献[11]推导了普通平底弹丸垂直跌落地面过程的冲击加速度峰值和作用时间理论计算公式,结合ANSYS/LS-DYNA软件仿真,得到了裸态平底榴弹底向下垂直跌落时弹丸和引信的冲击特性公式。文献[12]考虑弹底激励经弹-引系统传递后产生的影响,提出了引信后坐机构的一种工程设计方法,使设计精度得到提高。文献[13]对引信典型后坐机构平时安全性的计算方法与运动特性进行了研究,指出机构在坠落时的运动行程与在引信体上测得的冲击加速度时间历程的积分即速度呈线性关系,并给出了计算公式。
文献[14]运用动力学方法对弹丸跌落时的引信惯性部件运动规律进行了分析和仿真,指出引信惯性部件的最大位移出现在最大碰撞冲击加速度结束后,即当碰撞冲击力消失后,惯性部件依靠自身惯性继续压缩弹簧。在发射过载作用下,由于发射过载作用时间长,后坐保险件可以保证在发射过载消失前解除保险;在跌落冲击作用下时,冲击力作用时间短,惯性部件在跌落冲击力消失前和消失后均较难解除保险。
虽然目前后坐保险机构已广泛应用于各类引信及引信安全和解除保险机构中,但未见有文献研究被保险件或其反恢复销对保险件的作用力对后坐保险件动态响应的影响问题。以往对后坐保险件的动态响应研究均忽略了摩擦的影响,做了简化,如《引信设计手册》、国家军用标准GJB/Z135—2002《引信工程设计手册》。从机构原理上讲,该摩擦普遍存在,可能是被保险件产生的,也可能是反恢复件产生的。
对于带弹簧预压作用的被保险件(如预压柱簧或锥簧推压的滑块,又如预扭的扭簧推扭的转子),当后坐保险机构为其第一道保险时,在后坐保险机构解除保险以前,保险件与被保险件直接接触对被保险件形成限位。保险件与被保险件相对运动或有相对运动趋势时,保险件将受到被保险件的摩擦阻滞作用,并对保险机构的性能产生影响,包括解除保险可靠性和勤务处理安全性。本文针对此问题,根据刚体动力学理论和ADAMS动力学仿真,研究预压簧直接或通过其他零件间接作用于后坐保险件上的摩擦力对后坐保险件在发射和跌落时动态响应特性(解除保险运动)的影响,试图找出规律,从而为后坐保险机构动态性能的设计优化提供参考。事实上,除上述引信隔爆件解除保险用预压簧对隔爆件的后坐保险机构解除保险运动有摩擦阻滞缓释作用之外,引信后坐保险机构的反恢复机构或称闭锁机构(多为压缩柱簧或预扭扭簧直接或通过柱销顶压在后坐保险件上)对后坐保险件的解除保险运动的影响本质上是相同的。
1 有侧向预压簧产生摩擦缓释作用的引信后坐保险机构
一种迫击炮弹引信单自由度后坐保险机构如图1所示,该保险机构的直接被保险件为受弹簧预压力作用的滑柱。该结构主要由惯性筒、惯性簧、引信体、滑柱簧、滑柱等组成。其中惯性筒为后坐保险件,滑柱为被保险件,引信体为结构件,惯性簧和滑柱簧是抗力件,装配状态下惯性簧和滑柱簧均存在一定的预压。在此不考虑隔爆件(滑块,未画出)对滑柱的影响。
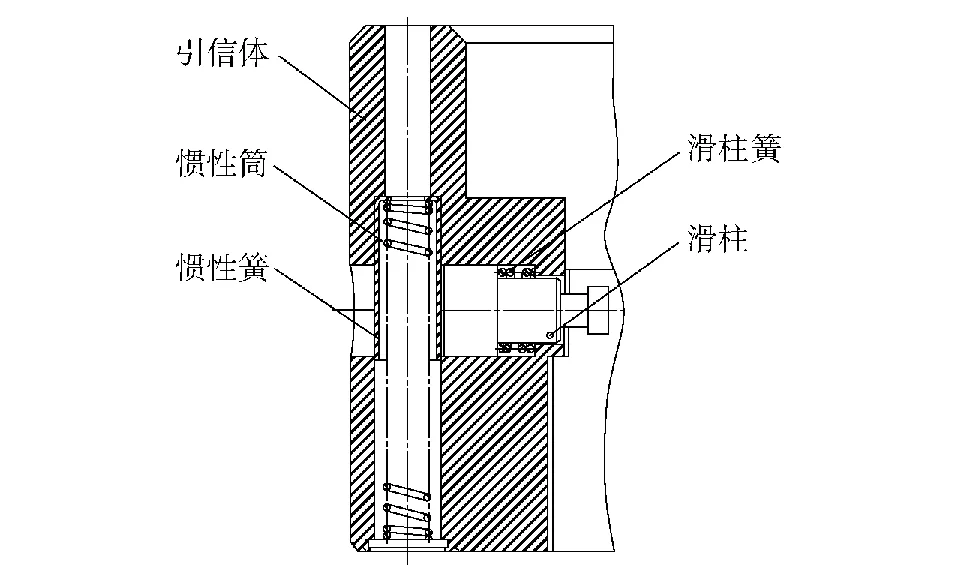
图1 有侧向预压簧产生摩擦缓释作用的引信后坐保险机构Fig.1 Setback arming device of a fuze with frictional retardation from loaded spring
弹丸或引信勤务处理意外跌落时,惯性筒在其运动方向上受到的外力主要有:跌落冲击产生的惯性力、惯性簧预压形成的支撑力、引信体约束形成的摩擦力和支撑力以及滑柱的正压力和摩擦力。若惯性筒受到的跌落冲击产生的惯性力小于或等于上述惯性簧支撑力和各种摩擦力的合力,则惯性筒将不产生运动,后坐保险机构不会解除保险;若跌落冲击产生的惯性力大于上述诸力的合力,则惯性筒将产生运动。若运动距离小于解除保险行程,则后坐保险机构也不会解除保险(跌落冲击过程结束后,后坐保险机构会恢复,即恢复保险),后坐保险机构满足勤务处理跌落安全性要求。若惯性筒发生运动且运动距离等于或大于解除保险行程,则惯性筒将意外解除保险,后坐保险机构不满足跌落安全性要求。
同理,弹丸发射时,惯性筒将受到发射过载的作用,若发射过载作用于惯性筒上产生的后坐力大于惯性筒受到的上述诸力的合力,则惯性筒将发生后坐运动。若惯性筒可以运动至解除保险位置,则该后坐保险机构设计参数满足解除保险要求。
2 有侧向预压簧产生摩擦缓释作用的引信后坐保险机构解除保险运动数学模型
2.1 建立惯性筒相对于引信体运动的惯性坐标系
单自由度后坐保险机构为典型的2阶线性无阻尼弹簧-质量系统。下面按牛顿力学的方法对其受力和运动特性进行分析,并建立数学模型。
为简化分析计算过程,利用作用时间0≤t≤T/2(T为正弦激励的周期)的正弦简谐激励,近似等效发射时的后坐过载曲线,取最大后坐过载系数为k1,则任意时刻t引信后坐保险件因冲击产生的惯性力为Ft,Ft=k1mgsin(ωt),其中m为后坐保险系统的等效质量,m=m1+m2,m1为后坐保险件的质量,m2为惯性簧的质量,ω=2π/T。当k1取跌落时的最大冲击过载系数时,Ft表示跌落时引信零件上形成的惯性冲击力,相应地时间周期T也需根据跌落过载脉冲时间宽度选取。
对解除保险前的惯性筒进行受力分析。将参考坐标系固连于引信,弹丸发射时随同引信一起平动和转动。由于引信后坐保险机构解除保险运动在最大膛压点以前完成,该阶段弹丸速度和转速都很小,即使是配用于旋转弹,也不考虑离心力的影响。
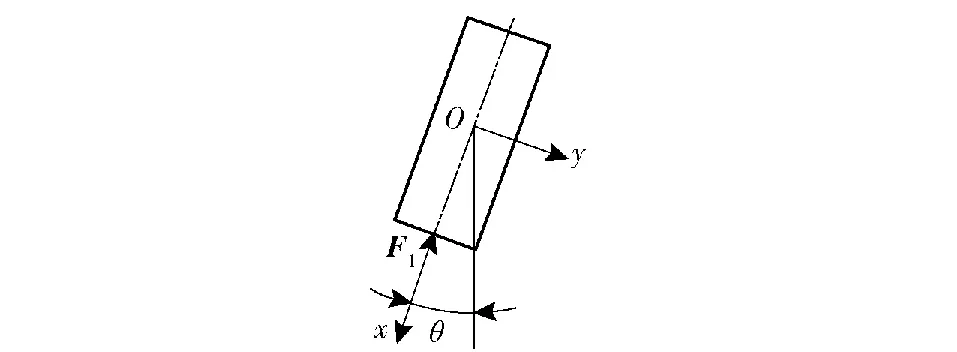
假设引信(弹丸)轴线与竖直方向呈θ角倾斜跌落,不考虑惯性筒与其驻室之间的间隙导致的惯性筒微小偏斜,只考虑惯性筒平动,则图1所示的后坐保险机构在倾斜跌落时其惯性筒的受力如图2所示。图2中,Oxy为固连于引信体的惯性坐标系,f1为惯性筒驻室侧壁对惯性筒的摩擦力,F0为惯性筒驻室上端对惯性筒的支撑力,F1为惯性簧对惯性筒的支撑力,F2为滑柱对惯性筒的正压力,f2为滑柱对惯性筒的摩擦力,Ft为惯性筒受到跌落冲击过载产生的惯性力,Ftx为Ft平行于惯性筒运动方向的分力,Fty为Ft垂直于惯性筒运动方向的分力,FN为惯性筒驻室侧壁对惯性筒的正压力。
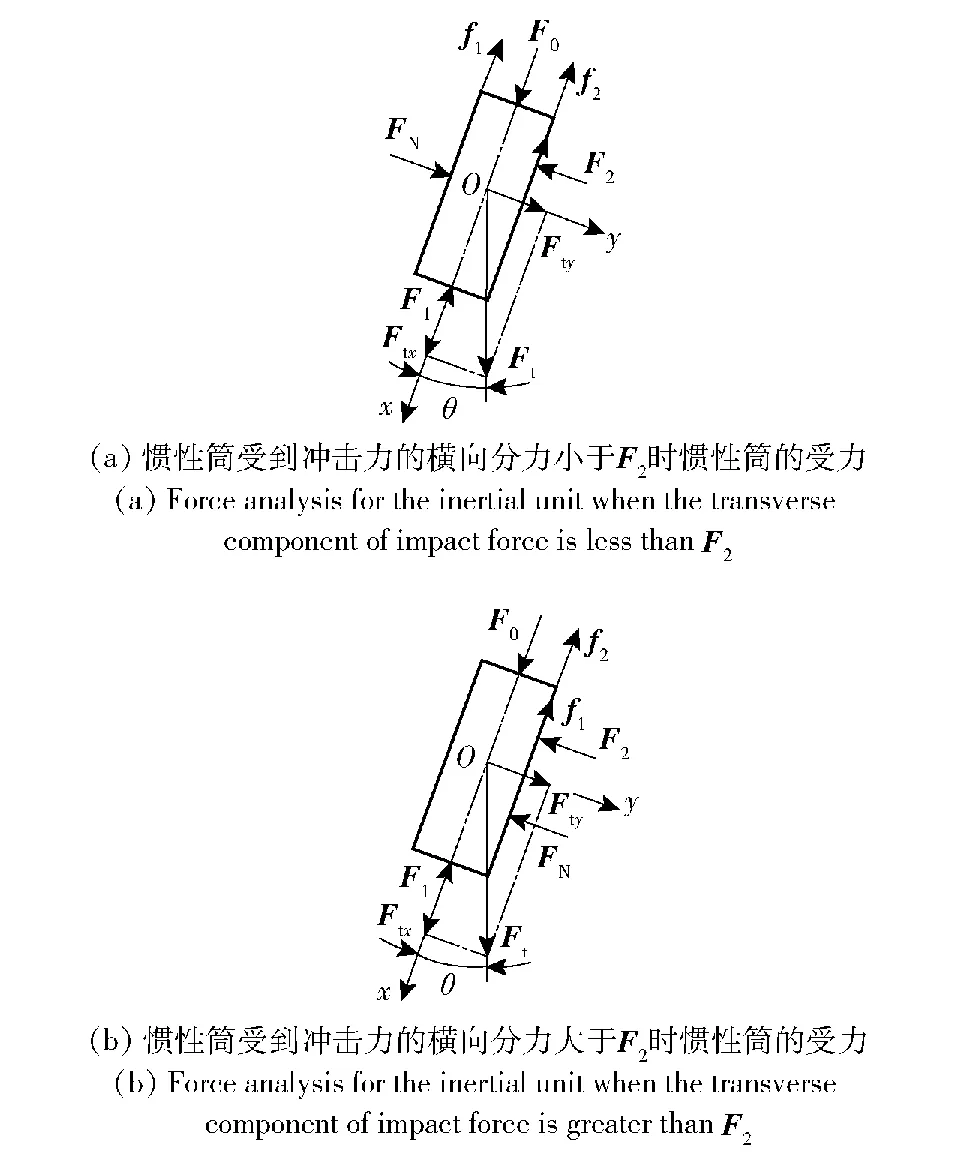
图2 引信(弹丸)倾斜跌向目标时惯性筒的受力Fig.2 Force analysis for the inertial unit as the fuze or projectile drops inclinedly
取初始时刻惯性筒质心为坐标原点,惯性筒的运动方向为x轴(向下为正)建立坐标系,得到惯性筒各阶段的运动方程,设惯性簧的初始预压长度为λ1,惯性簧刚度为K1。倾斜跌落状态滑柱对惯性筒的正压力F2与滑柱的运动状态有关。
2.2 滑柱的受力及运动数学模型
对于滑柱,受到的惯性冲击力可以近似为Ft2=k1m3gsin(ωt),其中m3为滑柱-滑柱簧系统的等效质量,m3=m30+m31,m30为滑柱的质量,m31为滑柱簧的质量。
倾斜跌落状态下滑柱受到的跌落冲击产生的惯性力Ft2可分解为垂直于滑柱运动方向的分力Ft2x和平行于滑柱运动方向的分力Ft2y。
(1)
引信或弹丸受到跌落或发射冲击过载作用期间,假设滑柱因冲击过载作用脱离与惯性筒的接触后,滑柱不再返回与惯性筒接触,则仅初始阶段,即滑柱保持静止且没有运动趋势的阶段(假设0≤t≤t20)(t20为滑柱开始相对于引信体有运动趋势的时刻),滑柱与惯性筒之间存在作用力。图3所示为该阶段滑柱的受力状态示意图,其中F′2为惯性筒对滑柱的正压力,f′2为惯性筒对滑柱的摩擦力,F3为滑柱簧对滑柱的支撑力,FN2为滑柱驻室与滑柱之间的正压力。
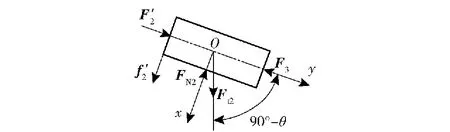
图3 引信(弹丸)倾斜跌向目标的初始阶段滑柱的受力Fig.3 Force analysis for the slide pin in the initial stage as the fuze or projectile drops inclinedly
此时,Ft2y≤F30,F30为滑柱簧预压力。滑柱受力满足以下关系:
(2)
式中:K2为滑柱簧的刚度;λ2为滑柱簧的预压长度。
由式(1)和式(2)可得该阶段惯性筒对滑柱的正压力:
F′2=K2λ2-k1m3gsinθ·sin (ωt)
(3)
到t=t20时刻(t20 (4) 对于惯性筒,倾斜跌落状态下的跌落惯性力Ft可分解为平行于惯性筒运动方向的分力Ftx和垂直于惯性筒运动方向的分力Fty: (5) 惯性筒的动摩擦系数和静摩擦系数在惯性筒的位移响应、速度响应中均处于同等地位,故可假设惯性筒与引信体以及惯性筒与滑柱间的动、静摩擦系数均为μ,则有 (6) 此时惯性筒的受力可分为3个阶段,在此设惯性筒相对于其驻室即引信体的运动时刻为t10,冲击过载结束时刻为t12,惯性筒减速到0 m/s的时刻为t13。 2.3.1 第1~1阶段(0≤t≤t10) (7) 根据式(7)和式(3),得 (8) 2.3.2 第1~2阶段(t10≤t≤t12) 假设从惯性筒开始相对于其驻室即引信体运动时刻(即t10时刻)到t11时刻,惯性筒受到的横向分力Fty小于F2;从t11时刻开始惯性筒受到的横向分力Fty大于F2。 在t10≤t≤t11阶段,惯性筒驻室即引信体孔壁对惯性筒的正压力FN与F2方向相反,此时惯性筒受力如图2(a)所示。 (9) 式中:x为惯性筒相对于引信体的位移量。 在t11时刻,由Fty(t11)=F2(t11)以及式(9)和式(2),可解得 (10) 由于0≤sin (ωt11)≤1,0 rad≤θ≤π/2 rad,故由式(10)可得 (11) 因此,当θ<θmin时,Fty(t11)=F2(t11)无解,即在t10≤t≤t12阶段恒有Fty 由此可知,θ≤θmin时,惯性筒在t10≤t≤t12阶段受力均满足式(9),F2满足式(3)。 求解式(9),可得t10≤t≤t11时惯性筒的位移响应如下: x=D4+D3sin (ωt)+D1cos (ωnt)+D2sin (ωnt) (12) 式(12)对时间t求导,得到如下速度响应: (13) (14) (15) 将式(14)、式(15)代入式(12),得到t10≤t≤t12时的惯性筒位移响应为 (16) 当θ>θmin时,由Fty(t11)=F2(t11)可得t11有两个解,分别为 (17) 或 (18) 即t10≤t≤t11或t12≥t≥t′11时,Fty≤F2,此时惯性筒受力仍满足式(9),F2满足式(3)。 当t11 (19) 由式(19)可知,该条件下惯性筒的运动状态与滑柱对其的正压力F2无关。 当t=t11时,FN=0 N,式(9)与式(19)相同。 求解式(19),可得t11≤t≤t′11时惯性筒的位移响应: x=D4+D5sin (ωt)+D6cos (ωnt)+D7sin (ωnt) (20) 式(20)对时间t求导,得到速度响应为 (21) (22) (23) 当t′11≤t时,惯性筒的受力满足式(9),可得其位移响应为 x=D4+D3sin (ωt)+D8cos (ωnt)+D9sin (ωnt) (24) 式中:D8、D9为惯性筒在该阶段运动微分方程的两个系数,可由惯性筒在该阶段的运动起始状态求得速度响应为 (25) (26) (27) 将式(26)、式(27)代入式(24),可以得到t′11≤t≤t12时惯性筒的位移响应。 2.3.3 第1~3阶段(t12≤t≤t13) 跌落冲击结束后,跌落过载消失,若惯性筒仍继续向下运动,则惯性筒的受力如图4所示。假设t=t13时刻惯性筒速度减为0 m/s。 图4 冲击过载消失后惯性筒做惯性运动时的受力Fig.4 Force analysis for the inertial unit when the shock overload disappears 此时,惯性筒的受力满足 (28) 为计算方便,假设过载消失时刻为时间零点,惯性筒受摩擦力和惯性簧支撑力作用(忽略重力作用)下作减速运动,设此时速度为vr,位移为xr,弹簧压缩量为λ1+xr,则由式(28)可得惯性筒运动微分方程为 (29) (30) 式(30)对时间t求导,得到速度响应为 (31) 设t=t3时惯性筒的速度减小到0 m/s,由式(31)求解得到: (32) 将式(32)代入式(30),可求得惯性筒速度为 0 m/s时的位移x3,若x3≥h,则可判断能解除惯性筒对滑柱的保险;若x3 图1所示的一种迫击炮弹引信后坐保险机构设计参数如表1所示,现估取各摩擦系数分别为0、0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.50和1.00,计算惯性筒在发射和跌落时的态响应特性。根据文献[13,15-17]提供的试验或仿真数据,分别选取120 mm迫击炮的发射冲击过载和82 mm迫击炮3 m落高跌落不同目标时的冲击过载进行计算。选取典型的发射过载和跌落过载环境参数作为理论计算参数如表2所示,其中跌落过载1和跌落过载2分别为文献[17]中82 mm迫击炮弹3 m落高跌向水泥地面和钢板时的过载,跌落过载3为文献[15]中测试所得82 mm迫击炮弹尾部向下1.5 m跌向钢板时的过载,跌落过载4为文献[18]中仿真计算所得130 mm杀爆弹底部向下1.5 m跌向钢板时的过载。 表1 一种迫击炮弹引信后坐保险机构设计参数 表2 计算用弹丸发射过载和跌落过载参数 根据第2节给出的理论公式,编制MATLAB计算程序,计算得到不同冲击过载作用下惯性筒的位移和速度响应。当惯性筒解除保险或未解除保险但向下运动的速度降为0 m/s时,停止计算,之后的运动不再考虑。通常认为动摩擦系数是静摩擦系数的0.8~1.0倍,以下计算均假设静摩擦系数等于动摩擦系数。 3.1.1 竖直跌落(发射)时惯性筒的运动特性 假设引信(弹丸)轴线与竖直方向的倾斜角θ为0°,分别取摩擦系数μ为0、0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.50和1.00,得到惯性筒在引信(弹丸)竖直向下跌落(或发射)时的位移响应-时间和速度响应-时间曲线,如图5~图9所示。 图5 发射过载作用下惯性筒的位移响应-时间和速度响应-时间曲线Fig.5 Displacement and velocity of the inertial unit under launch overload 图6 跌落过载1作用下惯性筒的位移响应-时间和速度响应-时间曲线Fig.6 Displacement and velocity of the inertial unit under drop overload 1 图7 跌落过载2作用下惯性筒的位移响应-时间和速度响应-时间曲线Fig.7 Displacement and velocity of the inertial unit under drop overload 2 图8 跌落过载3作用下惯性筒的位移响应-时间和速度响应-时间曲线Fig.8 Displacement and velocity of the inertial unit under drop overload 3 图9 跌落过载4作用下惯性筒的位移响应-时间和速度响应-时间曲线Fig.9 Displacement and velocity of the inertial unit under drop overload 4 其中图5为发射过载作用下惯性筒的位移响应-时间和速度响应-时间曲线,图6~图9分别为跌落过载1~跌落过载4作用下惯性筒的位移响应-时间和速度响应-时间曲线。 当摩擦系数μ取0~1.00时,在发射过载作用下惯性筒均能解除保险,且解除保险时惯性筒均有超过14.5 m/s的向下速度;在跌落过载1作用下,摩擦系数小于0.97时惯性筒均解除保险,摩擦系数大于0.97时惯性筒不解除保险;在跌落过载2作用下,摩擦系数小于等于0.30时惯性筒均解除保险,摩擦系数大于0.30时惯性筒不会解除保险;在跌落过载3和跌落过载4作用下,即使没有摩擦力作用,惯性筒向下的运动速度减小为0 m/s时,位移均未达到解除保险行程,故惯性筒不会解除保险。 3.1.2 倾斜跌落时惯性筒的运动特性 根据上述理论进行数值计算可得,在跌落过载1和跌落过载2作用下,分别以0.1°、0.2°、1.0°、5.0°角度倾斜跌落时,惯性筒的解除保险时间如表3所示;在跌落过载3和跌落过载4作用下分别以0.1°、0.2°、1.0°、5.0°角度倾斜跌落时,惯性筒均未解除保险,惯性筒的位移如表4所示。 表3 不同倾斜角度以跌落过载1和跌落过载2作用时不同摩擦系数对应的解除保险时间 表4 不同倾斜角度以跌落过载3和跌落过载4作用时不同摩擦系数对应的惯性筒最大位移 对比表3和表4中数据可知,对于有侧向预压簧产生摩擦缓释作用的引信后坐保险机构而言,若假设倾斜跌落时引信受到的跌落冲击过载不变,则与竖直跌落相比,倾斜跌落更不利于保证惯性筒的安全性。 由文献[19]可知,在弹丸倾斜跌向目标时产生的冲击过载会有大幅降低,由垂直跌落到1°倾斜跌落,冲击过载峰值减小很快,多数弹丸1°倾斜跌落时的跌落过载峰值小于垂直跌落时过载峰值的一半,即单从跌落冲击过载角度考虑,倾斜跌落条件下更有利于保证后坐保险机构的跌落安全性。 假设F2=0 N,可得无侧压簧作用时惯性筒的位移响应,即表3和表4中摩擦系数μ=0时的数据。对比可知有侧压簧的作用更有利于保证引信单自由度后坐保险机构的跌落安全性。 针对图1和表1所给出的一种迫击炮弹引信后坐保险机构建立虚拟样机,导入ADAMS刚体动力学仿真软件,建立仿真分析模型,如图10所示。根据设计完成模型材料属性赋值,定义接触、约束和弹簧,并施加外力。发射过载(或跌落过载)形成的惯性力施加在惯性筒质心,方向向下并随惯性筒一起运动,其大小和作用时间通过函数表达式定义。 图10 一种迫击炮弹引信后坐保险机构的ADAMS刚体动力学仿真模型Fig.10 Model of the setback arming device of the mortar fuze using ADAMS rigid body dynamic simulation 通过改变惯性筒与引信体之间、惯性筒与滑柱之间的摩擦系数,并根据表2中的过载参数改变施加在惯性筒上的冲击力,得到不同冲击过载作用下摩擦系数不同时惯性筒的质心位置变化曲线,结果如图11~图15所示。由仿真计算结果可知,在发射过载、跌落过载1和跌落过载2作用下,除个别摩擦系数特别大的3种情况之外,惯性筒均能解除保险;在跌落过载3和跌落过载4作用下,惯性筒的最大位移均小于解除保险行程,惯性筒不会解除保险。 图11 发射过载作用下不同摩擦系数对应的惯性筒质心位置变化曲线Fig.11 Change of center mass of the inertial unit with different friction coefficients under lunch overload 图12 跌落过载1作用下不同摩擦系数对应的惯性筒质心位置变化曲线Fig.12 Change of center mass of the inertial unit with different friction coefficients under drop overload 1 图13 跌落过载2作用下不同摩擦系数对应的惯性筒质心位置变化曲线Fig.13 Change of center mass of the inertial unit with different friction coefficients under drop overload 2 图14 跌落过载3作用下不同摩擦系数对应的惯性筒质心位置变化曲线Fig.14 Change of center mass of the inertial unit with different friction coefficients under drop overload 3 图15 跌落过载4作用下不同摩擦系数对应的惯性筒质心位置变化曲线Fig.15 Change of center mass of the inertial unit with different friction coefficients under drop overload 4 为研究摩擦系数对惯性筒解除保险运动的影响,并与数值计算结果进行对比,对于惯性筒能解除保险的情况,统计并对比得到在不同冲击作用下不同摩擦系数时惯性筒的解除保险时间,结果如表5所示;对于惯性筒不会解除保险的情况,统计并对比得到在不同冲击作用下不同摩擦系数时惯性筒的最大位移,结果如表6所示。 表5 不同冲击过载作用下不同摩擦系数对应的解除保险作用时间 表6 不同冲击过载作用下不同摩擦系数对应的惯性筒最大位移 1)理论计算结果与刚体动力学软件的仿真结果一致,两者可以相互佐证,说明结果是可信的。 2)预压弹簧作用的滑柱对惯性筒存在摩擦阻滞缓释效应,这种效应对后坐保险机构在跌落冲击作用下的位移响应影响较为明显,对后坐保险在发射过载作用下的位移响应影响很有限;跌落冲击过载1峰值与发射过载峰值相近,持续时间比发射过载要短,大幅增加滑柱与后坐保险件间的摩擦系数有助于该机构满足跌落安全性要求;跌落冲击过载2峰值比发射但持续时间远小于发射过载持续时间,该冲击条件下增加了摩擦缓释效应的后坐保险机构可以很好地保证跌落安全性要求。合理地设计滑柱簧的预压抗力和/或滑柱与惯性筒之间的摩擦特性,可明显改善后坐保险机构的跌落安全性,同时对后坐保险机构发射时解除保险的可靠性不会有明显的影响。 3)摩擦力对后坐保险机构的影响主要在惯性筒运动的第三阶段,即惯性减速阶段,增加摩擦力可使惯性筒的速度快速衰减到0 m/s,保证跌落不解除保险。 4)发射过载持续时间足够长,发射过载消失前惯性筒即可解除保险,惯性筒不存在第三阶段的运动,因此摩擦阻滞力对发射时解除保险可靠性影响很小。 5)在弹丸倾斜跌向目标时产生的冲击过载会有大幅降低,倾斜跌落条件下更有利于保证后坐保险机构的跌落安全性。 根据迫击炮引信后坐保险机构在发射过载、跌落过载1和跌落过载2作用下的响应可知,保险机构在发射时能可靠解除保险,在峰值与发射过载峰值相近、持续时间为毫秒级的冲击过载(跌落过载1和跌落过载2)作用时,不能很好地保证跌落安全性。根据理论分析,在不影响发射时解除保险性能的前提下,对该后坐保险机构参数进行优化计算。优化的参数包括滑柱簧的预压抗力F2和惯性筒与引信体孔壁、惯性筒与滑柱之间的摩擦系数μ,其余参数见表1。 由理论分析可知,摩擦力f1=f2=μF2,即滑柱簧的预压抗力F2和摩擦系数μ是以摩擦力f1和f2的形式对惯性筒的位移相应产生影响的。现选取摩擦力f1=f2=f在0~6 N范围内变化,按枚举法,计算得到不同摩擦力时惯性筒在不同冲击过载作用下的位移响应如图16所示。 图16 不同冲击过载作用下惯性筒的最大位移响应-摩擦力曲线Fig.16 Maximum displacement response-friction force curves of the inertial unit with different friction fficients under various impact overloads 由图16可知,摩擦力f小于4.20 N时可以保证惯性筒在发射过载作用下能解除保险,摩擦力f大于2.13 N时可以保证惯性筒在跌落过载1作用下不会意外解除保险,摩擦力f大于0.67 N时可以保证惯性筒在跌落过载2作用下不会意外解除保险。在跌落过载3和跌落过载4作用下,即使无摩擦阻滞力作用,惯性筒的最大位移也能保证小于解除保险行程,即惯性筒不会解除保险。 因此,若需同时满足跌落过载1和跌落过载2冲击下的跌落安全性要求,且满足发射时可靠解除保险要求,选取新方案参数μ和F2时,应保证f=μF2大于2.13 N,且小于4.20 N。为保证后坐保险机构具有一定的跌落安全性裕度和可靠解除保险裕度,应选取摩擦系数μ和滑柱簧预压抗力F2使摩擦力f处于其上述上、下限范围内并尽量远离上、下限。 本文针对具有弹簧预压作用的被保险件对后坐保险件的摩擦缓释效应,通过理论和仿真分析的方法,研究了该效应对后坐保险件在意外跌落和发射时动态响应的影响,得到了有侧压簧即被保险件预压簧作用时后坐保险件在多种不同冲击过载作用下的位移响应和速度响应。得出主要结论如下: 1)被保险件对后坐保险件的摩擦缓释效应有利于提高后坐保险机构的跌落安全性,而对后坐保险机构发射时正常解除保险影响十分有限。 2)对于部分跌落高度处于设计临界状态的引信后坐保险机构,被保险件与后坐保险件之间摩擦力的大小及有无,将直接影响其跌落安全性是否满足要求。 3)对于处于这种状态的产品,应严格控制后坐零件运动副表面的加工质量和摩擦系数。同时应控制被保险件弹簧的预压抗力以及抗力散布,预防预压抗力下限过小,影响跌落安全性。而对于带反恢复机构的后坐保险机构,反恢复件施力端头不平,或存在明显毛刺或硬棱,会使后坐保险件受到异常的阻滞力,可能影响后坐保险件在发射时可靠解除保险。 4)通过优化被保险件弹簧的预压抗力和/或被保险件与后坐保险件之间的摩擦特性,即优化后坐保险件受到的摩擦阻滞力,可使后坐保险机构的跌落安全性得到改善。对于受到过载峰值与发射过载峰值相近,作用时间达到毫秒级的跌落过载作用时,单自由度后坐保险机构安全性与作用可靠性之间的矛盾尤为突出,合理设计后坐保险件受到的摩擦阻滞力可以有效地解决该矛盾。 5)若倾斜跌落时引信受到的跌落冲击过载不变,则与竖直跌落相比,倾斜跌落可能导致侧压销(如前述滑柱)脱离,不利于保证惯性筒的安全性,但有侧压销仍比无侧压销更有利。通过优化侧压销结构,减轻侧压销的质量,可以降低倾斜跌落带来的不利影响。此外,也可以通过预扭的扭簧代替弹簧侧压销来解决倾斜跌落时侧压销脱离的问题。2.3 惯性筒的受力及运动数学模型
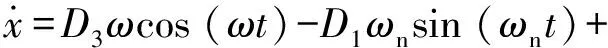
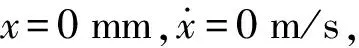

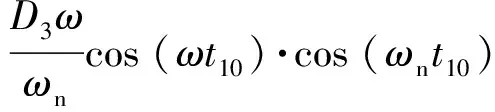

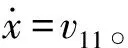
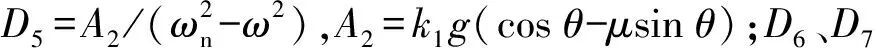
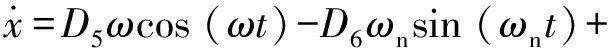
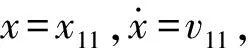
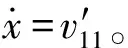

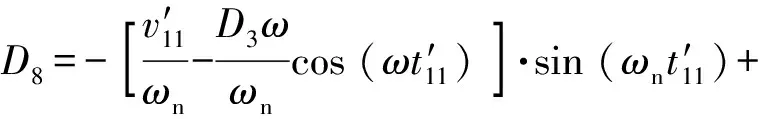
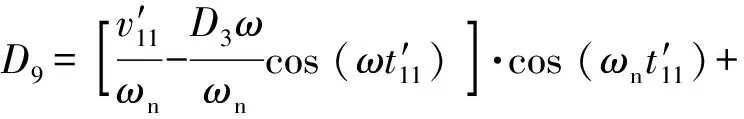
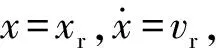
3 算例分析
3.1 数值计算

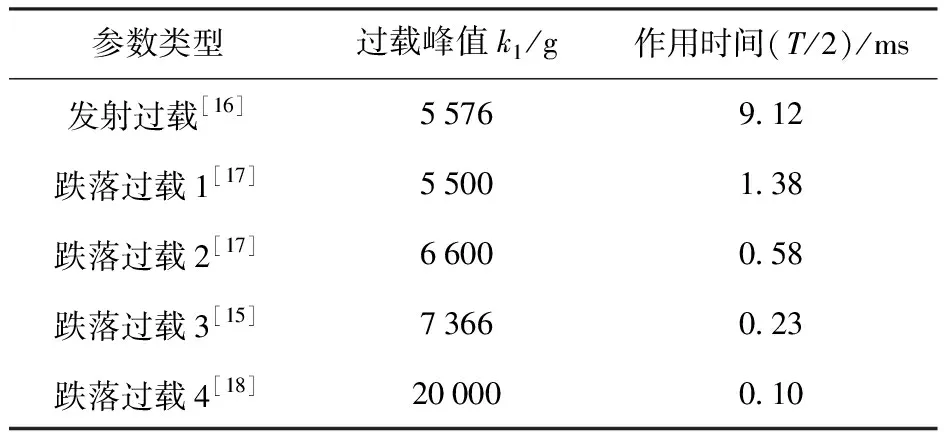


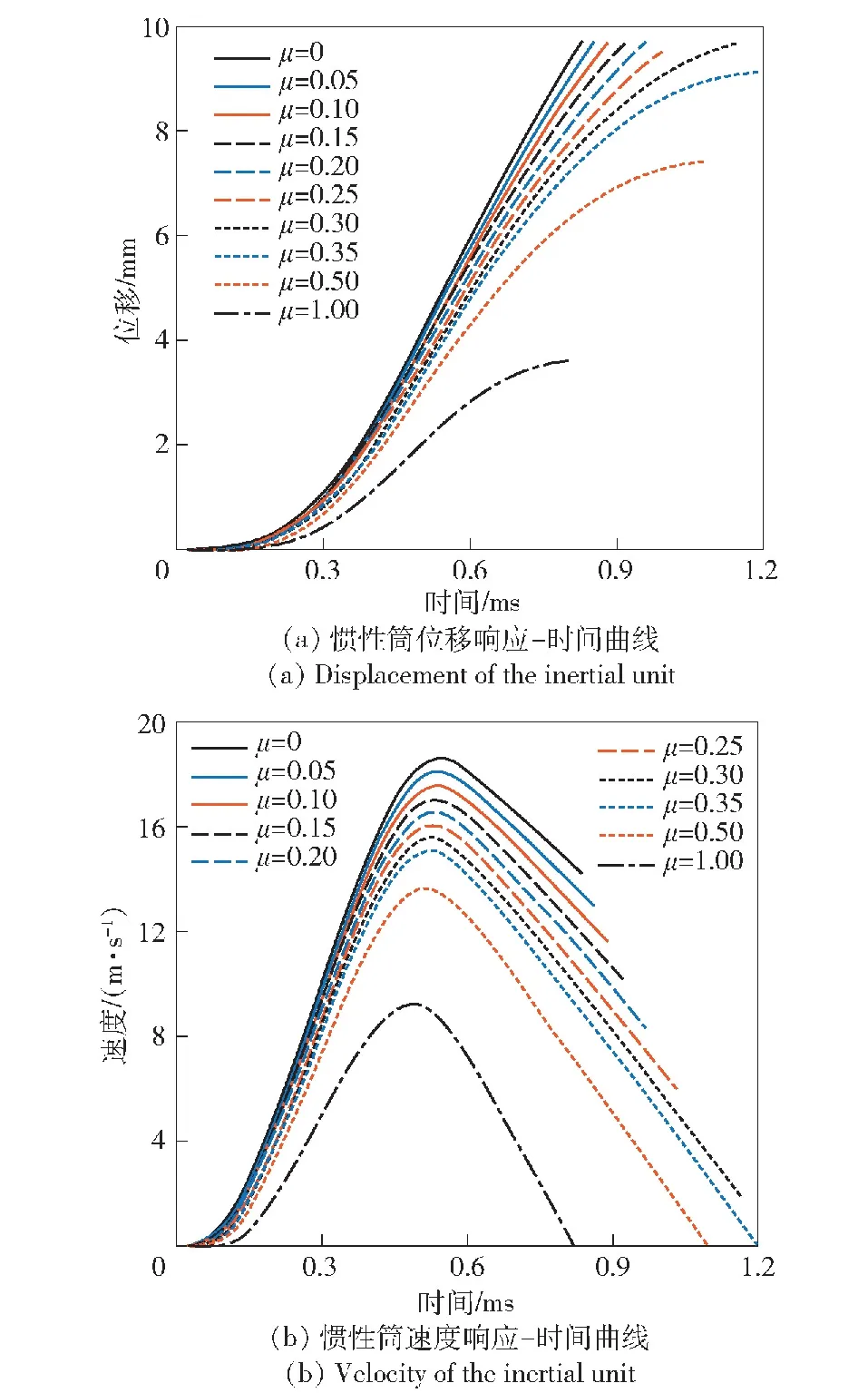
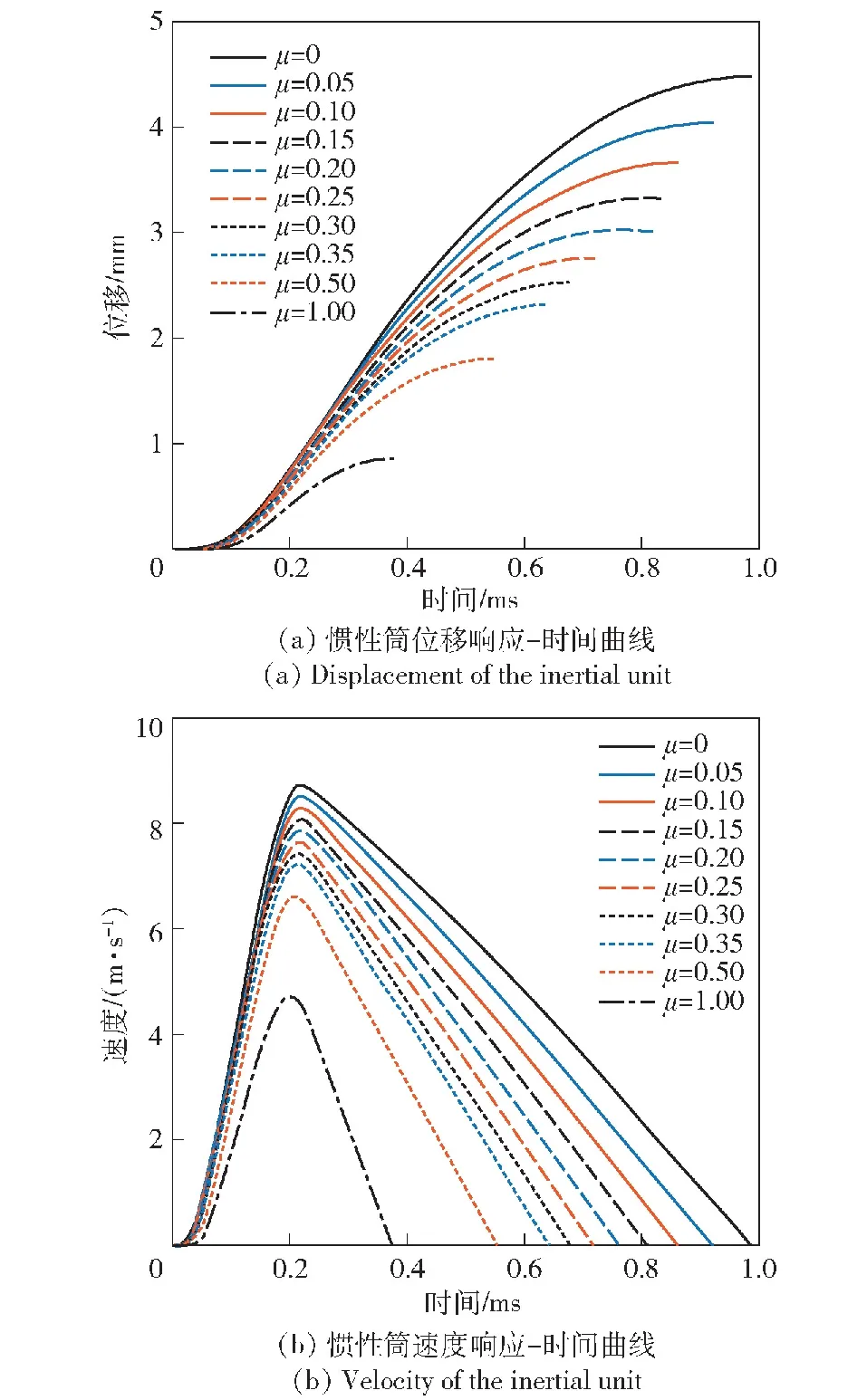
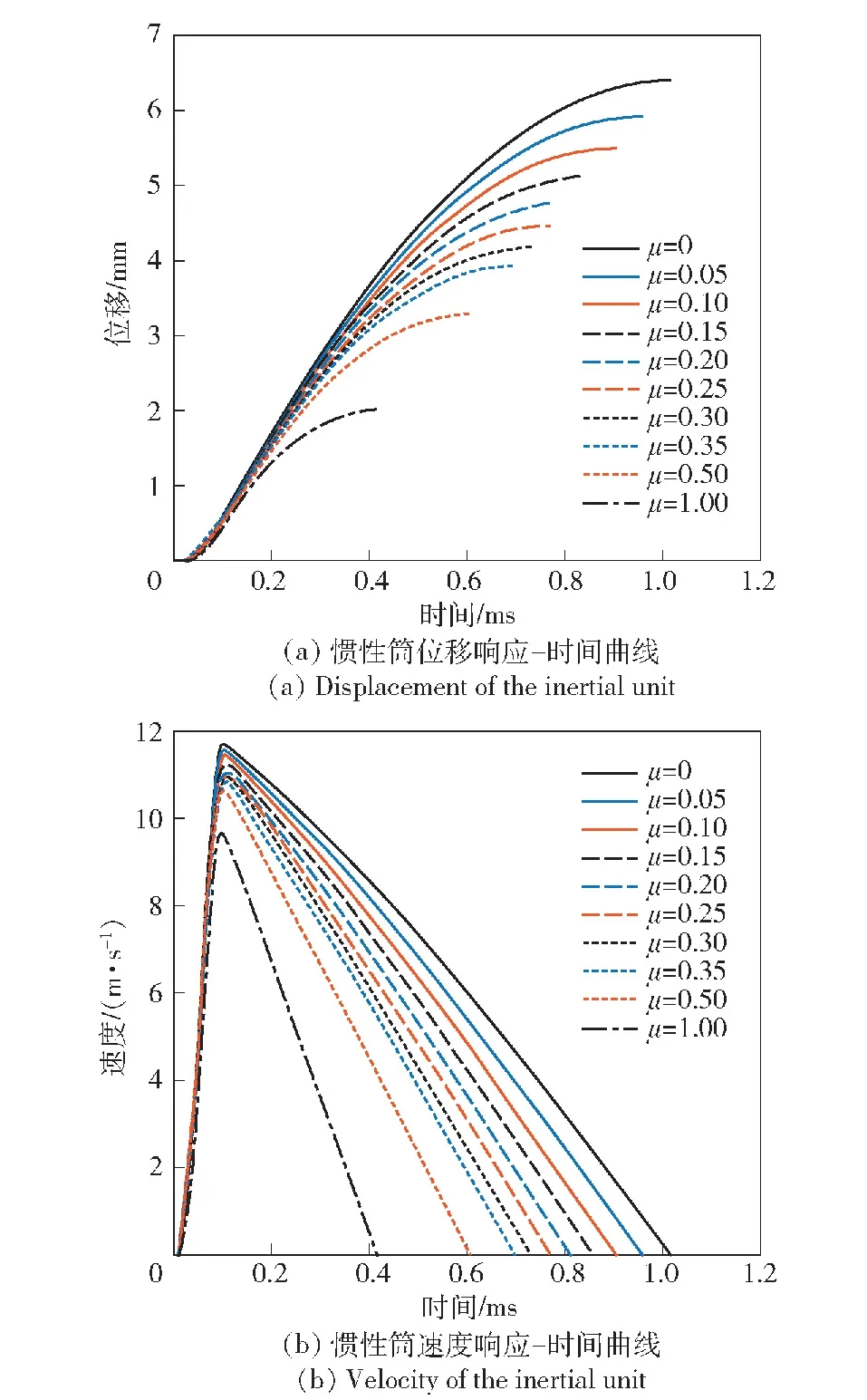
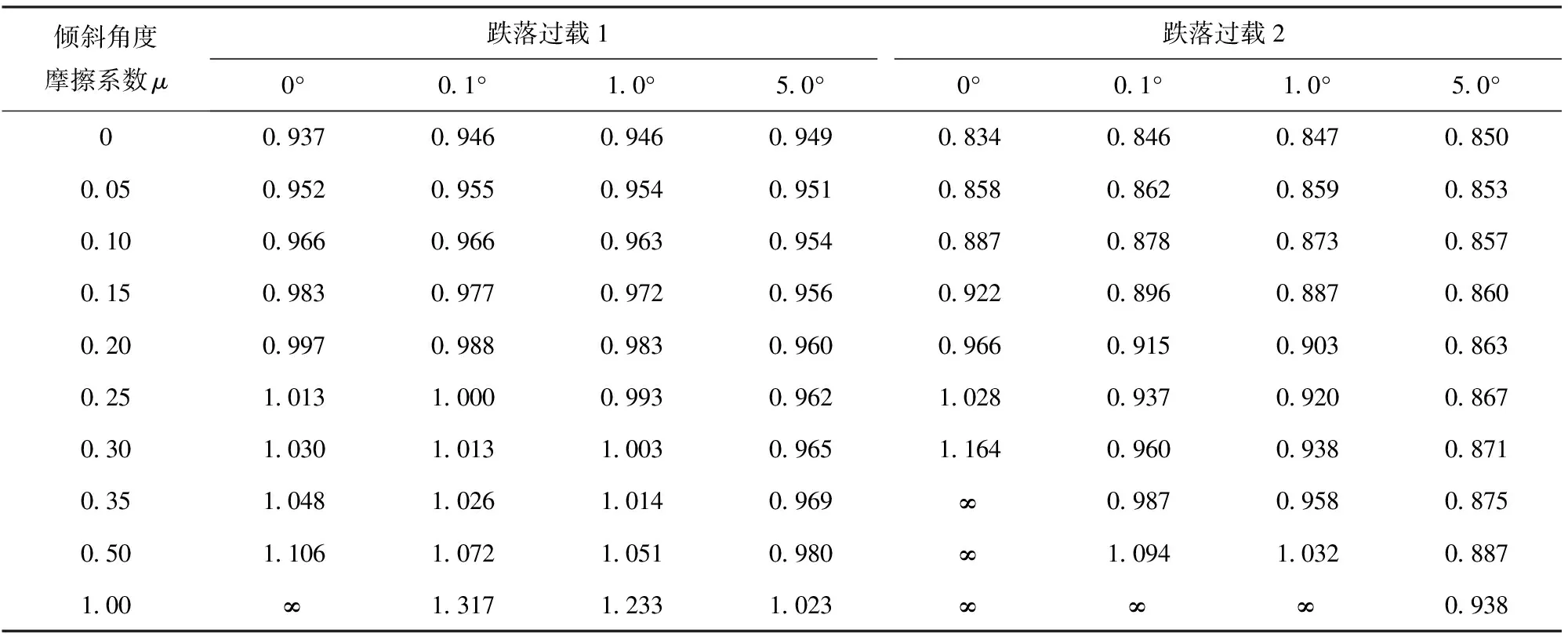

3.2 仿真分析

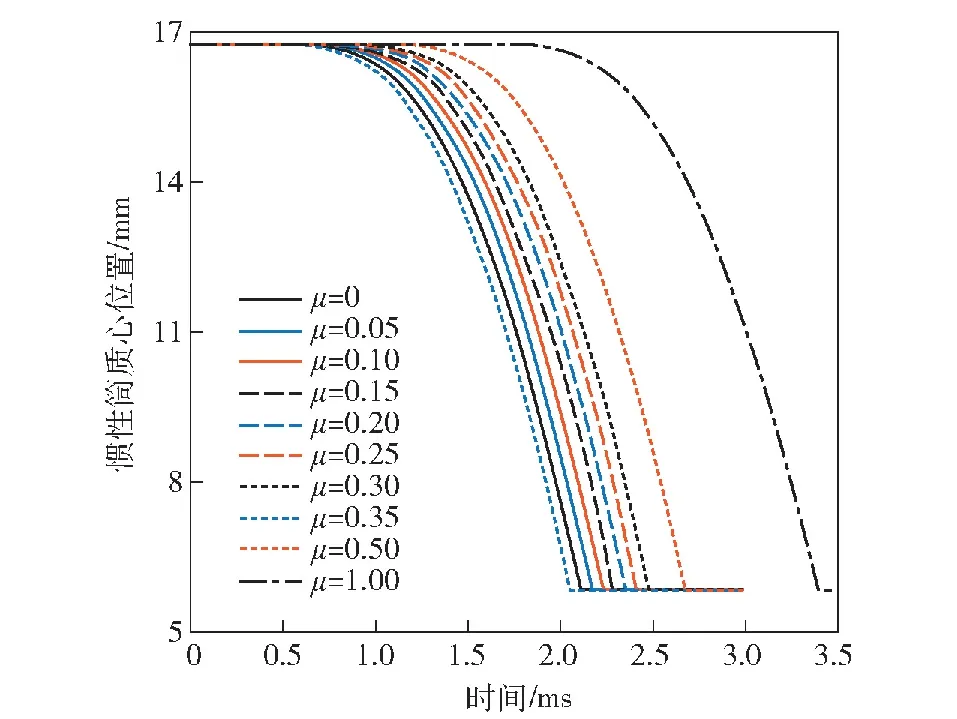



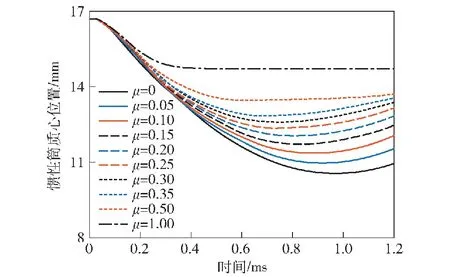

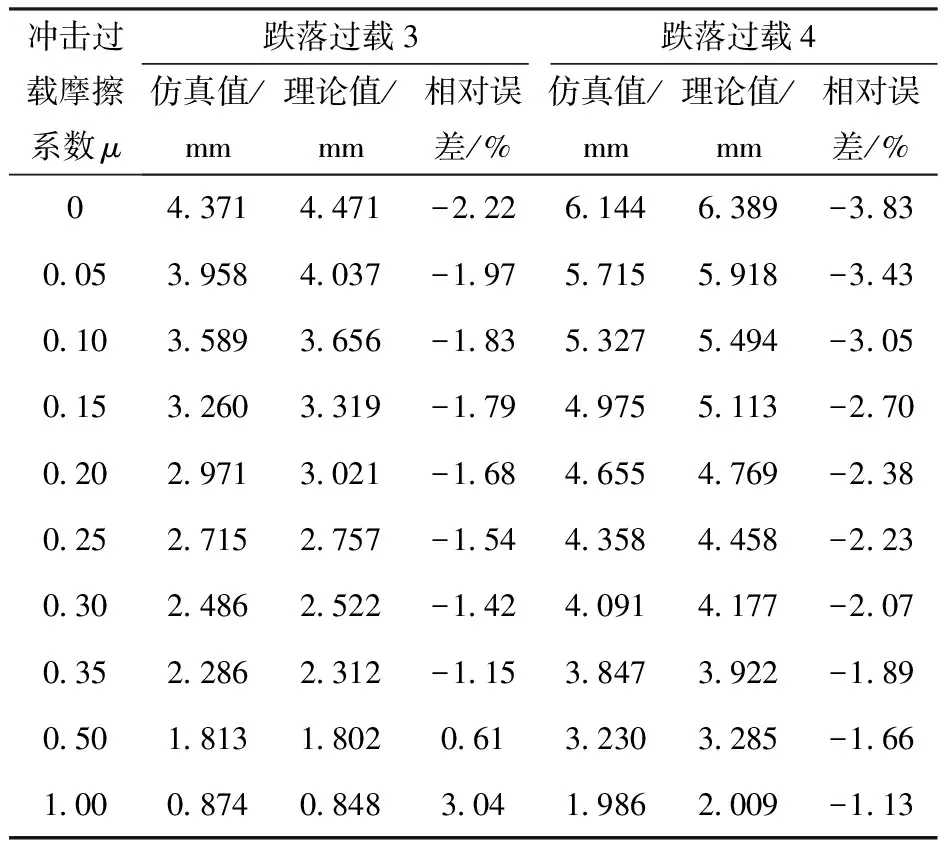
4 结果分析与改进
4.1 结果分析
4.2 设计改进

5 结论
