基于环形阵列的地面无人装备集群通信干扰抑制

穆巍炜, 何滨兵, 齐尧, 李子先, 张志超, 徐友春

(陆军军事交通学院, 天津 300161)

0 引言

现代战场中,地面无人装备集群作战日益受到重点关注[1]。个体智能与群体智能相结合,可以执行广域目标搜索、目标连续任务覆盖等传统车辆无法完成的复杂任务[2-4]。地面无人装备集群通信具有装备信息共享和动态分配能力,在特定应用场景中,良好的通信网络能够稳定可靠地执行信息交互[5-6]。考虑到地面无人装备集群通信在未来军事中的应用,设计一种能够波束形成和干扰零陷抑制的天线尤为重要,该天线既能使信号覆盖范围广,又能满足在恶劣的战场环境下保持较强的抗干扰能力,保持良好的通信网络。图1为地面无人装备集群通信示意图。

图1 地面无人装备集群通信示意图Fig.1 Schematic diagram of ground unmanned equipment trunking communication

文献[7]针对无线组网场景下相邻单元的同频干扰,提出一种结合动态频谱分配算法与功率控制的干扰抑制方法,但是没有分析动态频谱分配与多级软频率复用结合对干扰的抑制效果。文献[8]描述的功率倒置(PI)算法能够自适应感知功率较强的干扰方向并进行抗干扰,但在期望信号有益增长方面存在不足。文献[9]提出的双曲线抗跟踪干扰方法是在跟踪干扰原理的基础上通过排除跟踪干扰有效区域,并对其参数进行修改,最终可将跟踪干扰作用于干扰的无效域内。文献[10]针对干扰来向变化服从三角分布模型的信号假设提出了一种零陷展宽算法,但是在实际应用中必须已知波达方向信息才能实现较好的干扰抑制效果。文献[11]基于阵因子理论设计了五元全球定位系统阵,该系统阵中心频率为1.75 GHz,阵元间距为0.47λ(90 mm),λ为接收射频信号的波长,在阵列方向图(45°,30°)干扰方向上形成了-36 dB的零陷,具有一定的干扰效果,但是阵元间具有互耦效应。文献[12]通过捕获干扰信号计算出协方差矩阵,提出一种稳健的波束形成算法,该算法在可能出现干扰信号的范围内,将捕获的零点所对应的协方差矩阵及噪声协方差矩阵相加,重构出噪声与干扰协方差矩阵,但捕获零点的过程较为不易,容易产生误差,对算法结果影响较大。

上述文献提出的干扰零陷方法在一定程度上可以对信号进行干扰抑制,但是地面无人装备之间的通信不仅通视条件较差、信道环境恶劣[13],而且为完成某些特定任务,需要多装备、多方位实时通信,要求其天线具备高增益、多波束指向能力;同时集群组网中无人装备节点相对位置的不确定性及大动态范围调整,对天线覆盖范围、跟踪精度和扫描定位速度都提出了更高要求。本文设计的环形阵列天线采用大动态多波束快速数字形成方法,克服了传统全向天线增益低、伺服定向天线指向单一、覆盖范围小的缺点,并可通过波束零陷抑制多径干扰和同频干扰。

1 环形阵列接收信号模型

环形阵列天线采用M个微带平板天线作为阵元,天线模型如图2所示,实物图如图3所示。

图2 环形阵列模型(俯视图)Fig.2 Antenna array model (planform)

图3 环形天线实物图Fig.3 Photograph of the antenna array

以正上方目标波达角0°为基准,考虑远场信号s(t)以θ方向入射到空间天线阵列,天线阵列的规模为M个接收阵元,令θ为方位角,根据环形阵列排布得到阵元m接收信号对应的相位差为

(1)

式中:Δφ为相邻阵元间的夹角;Dm为相应阵元与波达角0°基准范围内的阵元数量,Dm=m+1;d为相邻阵元间的间距。

因此,天线阵列的规模为M个接收阵元的导向矢量为

(2)

则阵列的接收信号可以表示为

X(n)=AS(n)+V(n)

(3)

式中:A为导向矢量组成的阵列流型矩阵;S(n)为信号向量;V(n)为均值为0、方差为σ2的高斯白噪声向量。

2 算法集成设计

为实现水平全角域的有效接收,在阵列模型的基础上还需要采用相关算法来实现波达方向角(DOA)估计及多信号融合,进行数字波束赋形[14]。

在实际工程设计中,由于结构加工偏差和阵元加工不一致等误差会导致阵列流型与环形阵列理想模型不同,必然使数字波束赋形算法性能下降,波达角估计不准甚至估计错误,因此还需对其进行理想模型的工程化校正,即幅相校准[15]。

除上述情况以外,物理环境及集群场景使得电磁环境复杂,如何在众多信号中识别有效信号,则需要干扰抑制算法来实现。图4为基于环形阵列天线的集群通信干扰抑制实现步骤框图。

图4 集群通信干扰抑制步骤框图Fig.4 Block diagram of the trunking communication interference suppression procedure

2.1 通道幅相一致性校准算法

在阵列信号参数估计的实际应用中,影响阵列信号估计性能的主要因素有阵列位置扰动和互耦效应、通道间硬件设计引起的幅相偏差。

通常,采取对阵列流型直接进行离散测量、内插值和存储来校正阵列流型误差[16],但是阵列流型内插准确度不能与方位估计高精度要求匹配,存储会导致系统复杂度增大。因此,大量研究采取以阵列误差建模的方式,将阵列校正转化为参数估计问题。采用参数估计对阵列误差进行校正分为有源校正法和自校正法[17]。

在实际应用中,阵元位置和互耦效应这两类误差可通过对硬件设备的精密设计加工降低到容许范围内,因此本文主要对通道幅相不一致性进行校准。

空馈信号校正法通过对信号求相关来实现对阵列通道不一致性的校正,在校正阵列天线各射频通道间幅相误差的同时,还能够校正天线和馈线系统带来的误差。幅相校正实现框图如图5所示,校准前后比对结果如图6所示。

图5 幅相校正实现框图Fig.5 Block diagram of the calibration process

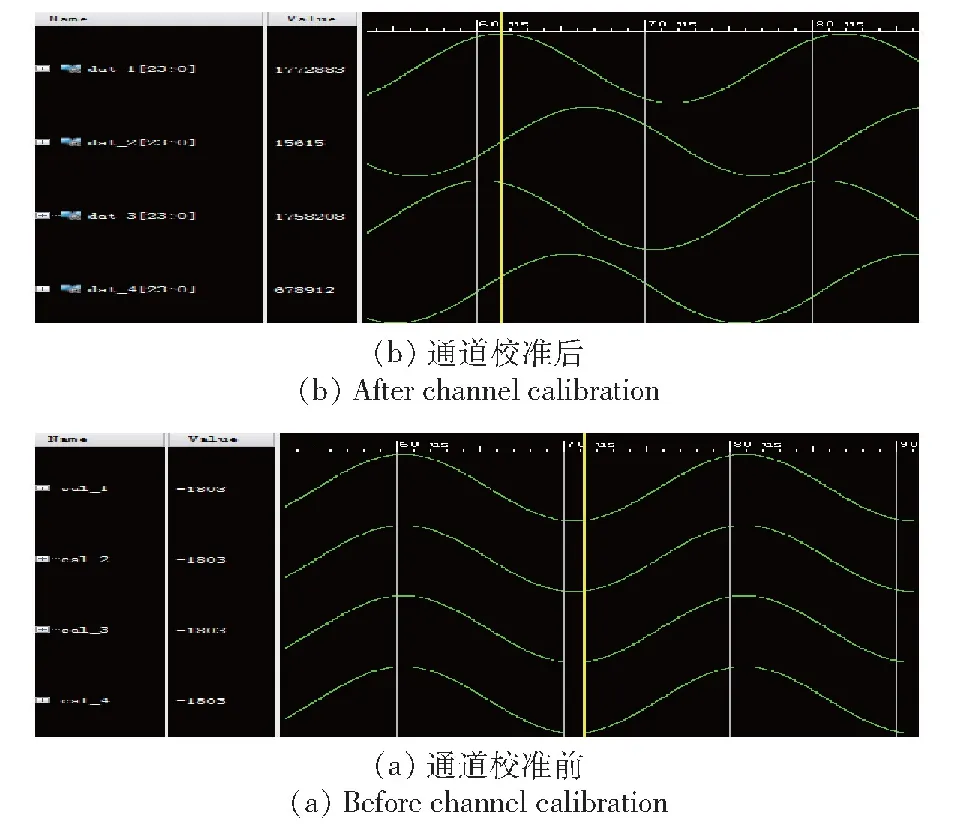
图6 通道校准前后对比图(左为输入信号幅度参数,右为时域波形图)Fig.6 Waveforms before and after channel calibration (the left image shows the amplitude of input signals, while the right is the waveform in the time-domain)

从图6中可以看出,幅相校正可以有效消除不同通道间的幅度和相位不一致性,从而为后续DOA估计与数字波束成形奠定了基础。

幅相校正具体实现步骤如下:

步骤1对阵列注入一个信号Tx,设基准通道为通道1,分配到要校准的第i(i=2,3,…,M)个通道的注入信号为Txi,设接收通道的幅相不一致性分别为gi,则第i个通道接收的数据Rxi为

Rxi=Txi×gi

(4)

步骤2用第一通道的信号代替Tx作为基准信号进行运算,用第一通道的接收信号Rx1的采样序列x1(k)(k=1,2,…,N)数据和其他通道接收的数据做相关运算:

(5)

式中:N为采样点数量。

步骤3设基准通道为通道1,计算其余通道与基准通道的幅相不一致性:

(6)

步骤4每个接收机中各个通道间不一致系数的倒数即为补偿系数,将其乘以各路接收信号即完成校准过程。

2.2 数字波束形成算法

2.2.1 空间谱估计算法

为提高方位估计的精度,本文采用多重信号分类(MUSIC)算法[18]实现超分辨测向空间谱估计,确定来波方向,完成DOA估计。该算法对于每个通道中的噪声均假设为不相关,故噪声相关矩阵是对角矩阵。协方差矩阵为正定的埃尔米特矩阵:

R=E[XXH]=ARsAH+σ2I

(7)

式中:E[·]表示求期望矩阵;X为阵列的接收信号矩阵;Rs为接收信号的协方差矩阵;σ2为噪声功率;I为单位矩阵。特征值分解后为R=EΛEH,E为协方差矩阵的特征矢量矩阵,E=[e1,e2,…,eM],e1～eM分别为特征值λ1～λM对应的特征矢量,Λ为协方差矩阵的特征值组成的对角阵,Λ=diag(λ1,λ2,…,λM),λ1～λM分别为R对应的M个特征值,满足λ1≥λ2≥…≥λJ≥λJ+1=…=λM=σ2。显然,由特征值的大小关系可将特征值分成两部分,有J(有效目标数量)个较大的特征值,其对应的特征矢量称为信号子空间的基矢量Es;有M-J个较小的特征值,其对应的特征矢量称为噪声子空间的基矢量En。由于矩阵Rs为正定阵,有

AHEn=0

(8)

任意入射信号的引导向量a(θ)均正交于噪声子空间,功率谱函数定义如下:

(9)

然后通过谱峰搜索P(θ)得到入射信号的DOA估计,P(θ)对入射信号波达方向的分布进行描述[19]。

谱峰搜索设计框图如图7所示。

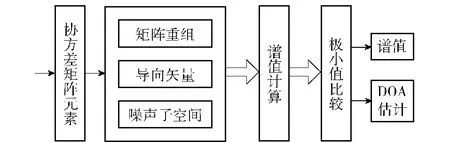
图7 谱峰搜索模块框图Fig.7 Block diagram of the spectral peak search module

首先对协方差矩阵进行特征值分解,然后采用噪声子空间与引导向量的正交性构造空间谱函数,寻找最小分母,搜索结束后输出频谱峰值和相应的DOA估计。

MUSIC算法可以有效估计多个独立信号的来波方向。然而当存在多径现象时,不同方向的入射信号不再独立,接收信号的协方差矩阵的秩将不再与DOA方向数相等,噪声子空间会扩散至信号子空间中,降低DOA估计的性能。对于多径导致的协方差矩阵缺秩现象,可以采用空间平滑算法[20]恢复协方差矩阵的秩。

空间平滑技术将环形阵列分为相互交错的K个等尺寸子阵,对各子阵分别计算协方差矩阵,并对各子阵的协方差矩阵取均值:

(10)

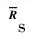
按照非相干信号的MUSIC算法计算功率谱函数,并通过谱峰搜索得到入射信号的多径DOA估计。理论分析结果显示,空间平滑算法可以有效改善多径信道下的DOA估计性能。仿真条件:环形阵元数M=16,阵元间距d=0.65λ,仿真采样点数1 024,目标地面无人装备数量为4,且来波角分别为15°、45°、315°和345°。采用空间谱算法得到空间谱如图8所示。

图8 4个子节点空间谱估计Fig.8 Spatial spectrum estimation of four child nodes

2.2.2 自适应波束赋形算法

为进行有效跟踪,完成对目标波达方向的获取后需对准目标,因此要设计固定波束。自适应波束形成如图9所示,各阵元信道将接收到的信号通过高速A/D转换为数字信号,得到合适的权值向量,根据环境参数的变化,通过自适应算法自适应地改变权值向量。图9中,Y(t)为阵列输出,W1、W2、…、Wn为第1～n路输入对应的权值,X1(t)、X2(t)、…、Xn(t)为阵列第1～n路输入信号。

图9 自适应波束形成框图Fig.9 Adaptive beamforming block diagram

在自适应波束形成算法[21]中,所有信号均为先验未知,盲算法中有基于信号特征、引导判决和基于DOA方法,其中基于信号特征只能用于恒包络信号,应用范围受限;引导判决虽算法简单,但精度低,不适用于地面无人装备集群通信[22]。

因此,本文采用基于DOA的Capon波束发生器,最小化噪声和来自θ以外方向的干扰所带来的功率,同时还可将观测方向θ上的信号功率保持恒定。其快速收敛的算法特性,适合地面无人装备集群作战场景。用数学表示为

(11)

式中:w为根据Capon算法选取的各通道加权向量。

仿真环境:环形阵元数M=16,阵元间距d=0.65λ,仿真采样点数1 024,来波角为(-15°,0°),采用自适应波束赋形算法的方向图如图10所示,在信号来向形成主波束,同时具有较低的旁瓣。

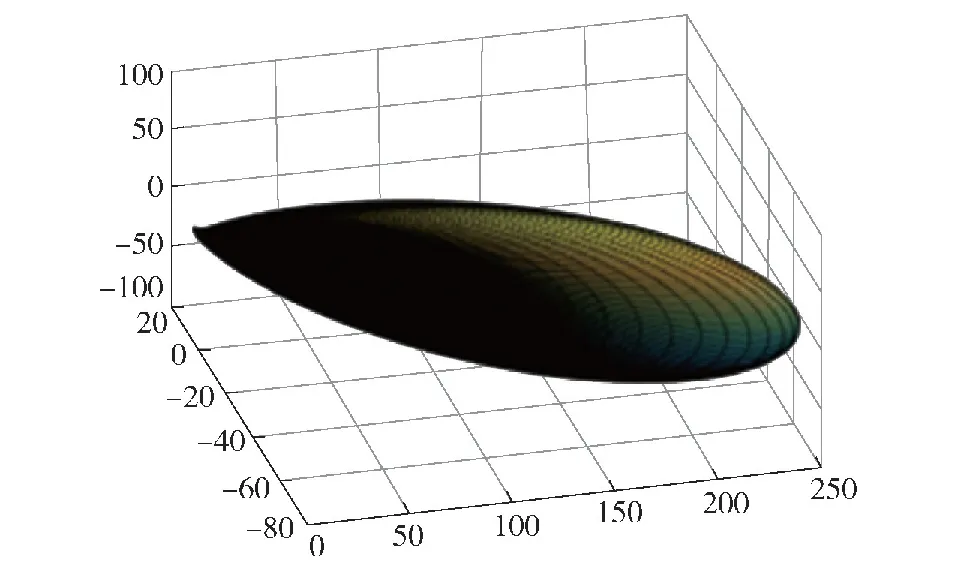
图10 2×4面阵环阵因子方向图Fig.10 Directional diagram of 2×4 circular array factors

2.3 干扰抑制算法

在干扰信号自身方向上自动形成零陷,就要对干扰信号进行最大限度的抑制。参考Capon波束成形方法的原理,在限定干扰方向增益的前提下,最大化其他方向的输出功率,即可实现对干扰方向的主动零陷。因此,干扰方向主动零陷的波束成形优化问题可以表示为:在Capon基础上改变目标函数迭代方向,取最大值(即功率值最小)[23]。对干扰方向用数学表示为

(12)

通过仿真图11(a)和图11(b)可见,干扰信号与子节点信号在空间上越接近,接收增益和干扰抑制的效果越差;通过仿真图11(c)和图11(d)可见,干扰信号越多,接收增益和干扰抑制越差,当干扰信号数量超过阵列天线自由度时,信号天线方向图显示其干扰抑制的性能急剧恶化。

图11 干扰信号与子节点信号方向图Fig.11 Direction diagram of interference signals and child node signals

3 仿真与分析

设单元天线增益7 dBi,3 dB波束宽度70°,按照本文设计的环形阵列方式组阵,使用MATLAB软件及ANSYS EM Suite软件进行仿真。

仿真1仿真得到子节点信号方位角0°指向时对应方向图增益约为14 dBi,3 dB波束宽度不低于22°,并在某一干扰方向(如干扰方向为45°,并可根据干扰抑制算法优化方向图)上形成20 dB零陷,如图12所示。可见,组阵后方向图增益增加7 dB,在干扰来向上形成了20 dB的抑制,总信干比改善了27 dB,既延展了通信作用距离,又有效提高了抗干扰能力。

图12 方位角0°指向增益方向图Fig.12 Azimuth 0°-pointing gain pattern

仿真2仿真得到3条曲线是子节点信号分别为0°指向、246°指向和360°指向的天线增益方向图,如图13所示。由此可见,本文设计的环形阵列天线可实现360°全方位面覆盖。可为地面无人装备之间集群通信增大信号覆盖范围。

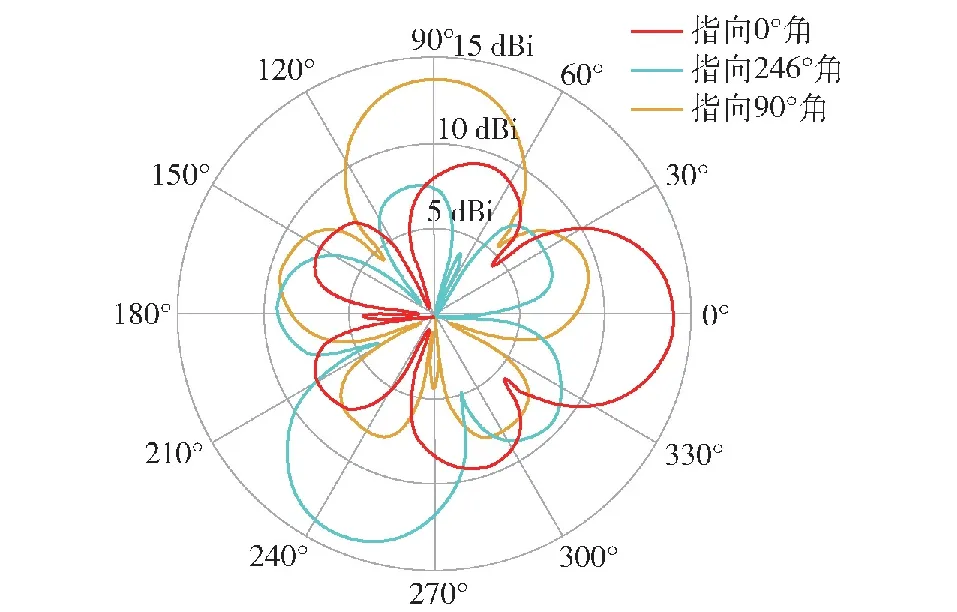
图13 不同方位角指向增益方向图Fig.13 Gain pattern with different azimuth pointings

4 结论

本文设计了一种基于环形阵列的幅相校准算法、波束形成算法与干扰抑制算法相结合的方法,该方法既能使天线信号覆盖范围广,又能满足在恶劣的战场环境下保持较强的抗干扰能力,保持良好的通信网络。对基于此方法设计的环形阵列天线进行了仿真,结果表明环形阵列天线可实现全方位多节点覆盖,覆盖范围广,可完成实时跟踪地面无人装备各节点波束指向;当监测到网络以外干扰源时,在干扰源方向可产生零陷,实现定向干扰抑制。该技术为地面无人装备集群组网大范围、网络化测控数据传输过程中,实现全方位扫描范围、快速波束形成、干扰抑制提供了有效解决方案。

本文考虑了阵列误差下的算法性能仿真,但在实际应用中,地面无人装备会面临各种复杂情况,如何处理复杂场景下产生的误差给测向算法带来的影响是提高天线性能的关键,也是下一步研究的重点。