基于非球形颗粒离散单元法分析单模块装药药粒散布特性

2023-05-31李梓钰余永刚

兵工学报 2023年5期

李梓钰, 余永刚

(南京理工大学能源与动力工程学院, 江苏南京 210094)

0 引言

模块装药点传火过程是影响火炮内弹道性能的重要环节,而点传火过程中模块药盒破裂、火药颗粒在药室内的飞散运动则可能影响压力波的产生和增长。这种压力波现象会对内弹道性能的稳定性产生影响,严重时可能引起膛内局部压力异常的升高从而造成弹丸早炸、膛炸等安全事故。

关于模块装药膛内压力波的研究,许多学者是将火药颗粒看作连续介质,建立欧拉-欧拉模型对压力波的影响因素进行试验和模拟仿真分析。如Ruth等[1]对155 mm XM216 模块装药进行装药安全性研究,探究常温和极端温度条件下内弹道循环过程中的点火、药床移动性和压力波的发展,发现模块盒体破裂前燃烧室内出现快速增压,点火循环后期压力波动较小。陆兵中等[2-3]基于短管试验炮,考虑模块运动性和初始装填分布的影响,对点火及扩散、压力波动的发展过程进行模拟和预测,发现火焰扩散期间膛内压力差较小,使得装药床移动速度慢、移动距离短;后又考虑药盒间的隔仓效应及环形间隙的作用等,对膛内压力波动进行精确模拟,发现相同装药量下,模块药盒材料的含能密度越低,膛内压差越小。王育维等[4-5]则从装药长度及模块盒体的能量特性两个角度对影响小号模块装药压力波的因素进行分析,依据两相流内弹道理论,发现随装药长度的增加,压力越稳定,压力波越小;模块药盒的火药力越大,则产生的压力波也越大。除此之外,他们还建立了双一维多相流内弹道模型,考察不同温度下模块药盒能量大小对压力波的影响。但随着计算机技术和相关理论的飞速发展,通过数值模拟从颗粒层次对压力波的影响因素进行研究成为可能。

在有关能源、化工、制药等工业生产以及农业、食品等领域中,为研究颗粒的动力学特性及其运动机制,国内外学者建立了多种数值模型对颗粒系统的复杂行为进行模拟,以探究试验难以获得的深层次、多尺度运动机理。其中,对于非球形颗粒采用DEM模型结合计算流体力学(CFD)的数值模型已成功应用于各种复杂流-固系统,如喷动床[6-10]、气力输送[11]、鼓泡流化床[12-18]等气-固两相流动过程。目前对于模块装药药粒散布的试验与仿真研究,是将药粒简化为球形颗粒进行模拟仿真[19-20],然而其实际形状更接近于柱状或杆状。并且当前研究普遍认为,颗粒的形状对颗粒行为具有较大影响。因此,在研究中应用球形颗粒假设得到的颗粒动力学特性极有可能与真实的非球形颗粒系统不同。

针对上述情况,本文以单模块装药火药床为研究对象,采用离散单元法模拟柱状火药颗粒的散布过程,对模块药盒破裂、柱状火药颗粒在药室内的飞散运动和堆积形态进行数值模拟。根据模拟结果,对单模块装药药粒散布特性进行深入分析,以期从颗粒层次上对单模块装药点传火过程中火药颗粒运动规律有更深入的理解和认识,进而为后续研究多模块装药点传火过程中药粒散布形态提供理论基础和手段。

1 物理模型

为更好地探究模块装药点传火过程中火药颗粒运动规律及其堆积形态,建立了该过程的数理模型,并为试验设计了可视化点传火平台,其结构图如图1所示,它由135 mm 口径的有机玻璃身管、击发点火装置、控压膜片等组成。身管由金属套筒固定,其上方开有测压孔,该孔还用于定位;药室右侧为半密闭端,装有控压膜片,使药室压力控制在安全极限值内。单模块装药点传火过程可简单概括为:首先击发点燃中心传火管内点火药包,点火药包燃烧产生高温高压燃气,随着压力不断升高,达到传火孔破孔压力,火药燃气和灼热固体微粒通过对流和辐射换热点燃发射药,模块药盒发生破裂,盒内未燃完的发射药会在药室内飞散运动,最终形成非均匀堆积散布。

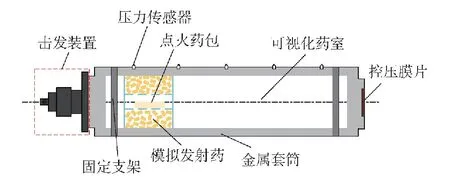
图1 可视化点传火试验装置结构图Fig.1 Schematic diagram of a visual experimental platform for the ignition and flame-spreading process

为充分考虑气相和固相间的相互作用以及固相颗粒间的碰撞,本文采用三维非稳态气-固两相流模型,并做如下假设:

1)用球元法构建的类圆柱形颗粒代替标准圆柱形颗粒,假设所有模拟药粒大小和形状完全相同;

2)模块药盒的破口压力约为10 MPa,且破口时药盒右端盖端瞬时全部破开;

3)模块药盒与药室等直径处理,不考虑药盒在药室内的运动;

4)采用Realizablek-ε(k为湍流动能,ε为湍流耗散率)湍流模型描述点火燃气射流的湍流流动。

2 数学模型

2.1 气相控制方程

气相控制方程包括连续性方程、动量守恒方程和能量方程,其表达式如下:

(1)

(2)

式中:ρg和εg分别表示气体密度和气体体积分数;ug为气体速度;p为气体压力;τg为气体黏度;g为重力加速度;S为气-固两相间的动量交换量。

2.2 柱状火药颗粒的接触模型及运动方程

本文采用球元法来描述柱状火药颗粒,如图2所示,图2(a)为标准柱状颗粒,图2(b)为3个球元构成的类柱状颗粒。由球元法构建的非球形颗粒,其受力和运动模型得到了简化,将颗粒与颗粒间、颗粒与壁面间的碰撞力转移到球元上计算,从而可以采用成熟的球形颗粒计算公式。但缺点便是引入了人为粗糙度,增加了颗粒摩擦力,并且随着构建颗粒所需球元数目的增多,颗粒受力计算误差增加,计算时间增加。根据Markauskas 等提出的计算人为粗糙度的方法,任冰[21]对不同方法构造的正方体颗粒的人为粗糙度进行计算并通过颗粒自由下落试验和堆积试验进行验证,发现随着构建球元数量的增加(用一种球元构建的情况下),所构建的颗粒与真实颗粒间的误差就越小。考虑试验所用模拟发射药粒的形状大小,本文采用3个球元构建柱状颗粒。

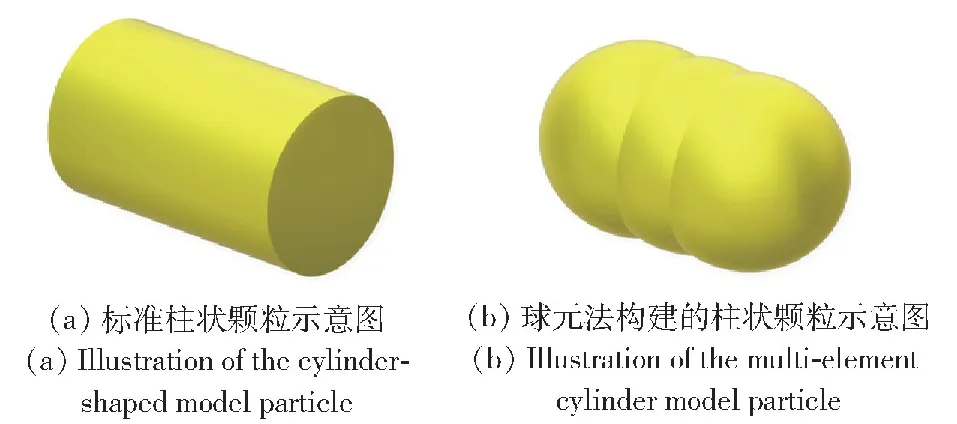
图2 柱状火药颗粒模型示意图Fig.2 Diagram of the cylindrical propellent pellets

由球元法所构建的柱状火药颗粒的碰撞接触形式可分为六类:球元-球元接触,球元-颗粒接触,颗粒-颗粒交叉接触,颗粒-颗粒平行接触,球元-壁面接触,颗粒-壁面接触,具体形式如图3所示。

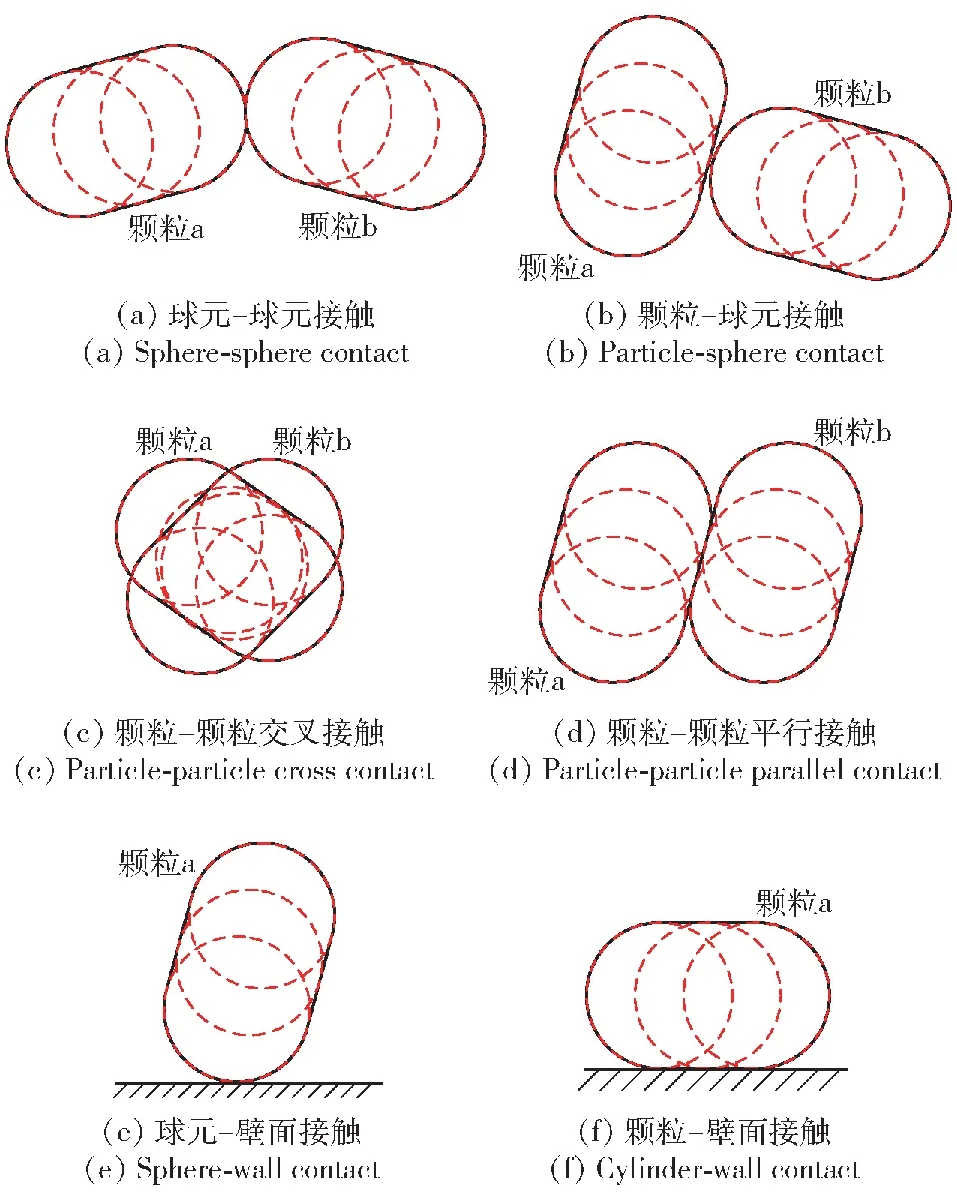
图3 柱状颗粒的碰撞机制Fig.3 Collision mechanism of cylindrical particles

图4为柱状颗粒碰撞后的受力示意图,颗粒主要受到重力、碰撞力以及气-固间作用力,其运动方式主要是平动和转动两种方式,由牛顿第二定律描述如下:

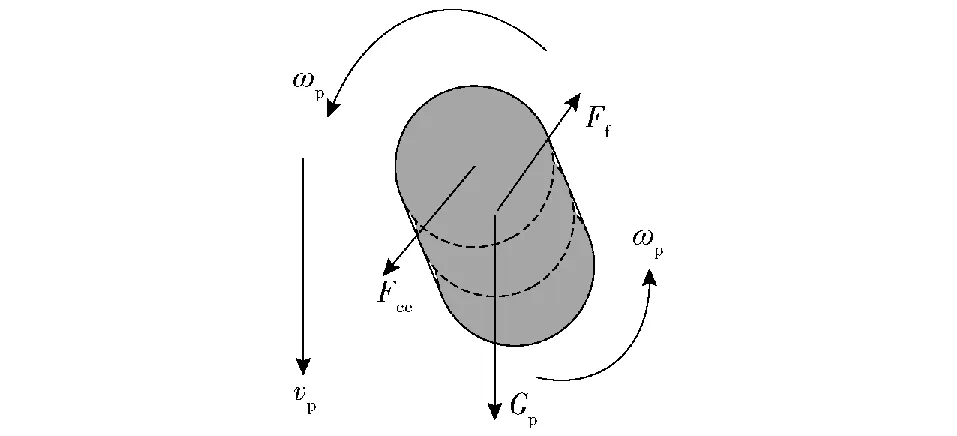
图4 柱状颗粒受力示意图Fig.4 Diagram of forces and motion of the cylinder pellet

(3)

(4)

式中:mp为柱状模拟发射药粒的质量;vp为颗粒的运动速度;Gp为颗粒的重力;Fc为碰撞力;Ff为气-固间作用力;Ip为柱状颗粒的转动惯量;ωp为颗粒的角速度;Tp为柱状颗粒转动的合力矩。每个柱状颗粒所受到的碰撞力是组成它的每个球元的碰撞力的总和,即

(5)

式中:Fce为组成柱状颗粒某球元j所受的碰撞合力;Ne为组成柱状颗粒的球元数量,本文取3。构成同一颗粒的球元间无相互作用力,颗粒-颗粒、颗粒-壁面间均采用Hertz-Mindlin无滑动接触模型[22]。

2.3 曳力模型

气相和固相间的曳力作用作为相间动量传递的主要方式将气-固运动耦合在一起,本文选取的是Free-stream曳力模型[22],即

Fd=0.5CdρgA|vp-g|vp-g

(6)

式中:A为颗粒的投影面积;vp-g为气体与颗粒的相对速度;Cd为曳力系数,

(7)

Re为雷诺数。

2.4 气-固相间耦合

本文中分别通过Fluent软件和EDEM软件进行CFD和DEM求解,CFD对流相信息进行跟踪,DEM对颗粒相信息进行跟踪。CFD首先由初始条件计算流相参数,然后将仿真控制权交给DEM;DEM根据流场信息和颗粒碰撞求解并更新颗粒的速度和位置等信息,并将此信息和控制权传回CFD;CFD根据返回的颗粒信息和流场信息计算该时间步长内的气-固相互作用力,计算当前网格的动量、能量源相等,进而完成一次耦合计算。

3 结果与讨论

3.1 DEM模型的验证

为便于记录和观察单模块装药点传火过程中药盒破裂、药粒飞散运动,建立可视化点传火试验平台。如图5所示,试验装置由半密闭爆发器点传火平台、压力传感器、数据采集及处理设备等组成。试验过程中压电传感器获得压力信号,经电荷放大器将电信号放大,再输入瞬态记录仪进行转换,最后通过计算系统进行数据的采集和处理,并且利用高速摄像机对单模块装药点传火的全过程进行记录。计算模型结构示意图及柱状颗粒平面模型如图6所示,模块药盒位于半密闭爆发器身管的左侧,与底火端的距离l0为40 mm,药盒右侧的药室空间则均为空气。模块药盒与药室身管壁的实际间隙为5 mm,但为了简化计算模型,模拟仿真时该间距忽略不计,且不考虑模块药盒与中心传火管的壁厚。为确保试验的安全性,药盒内仅装有少量的真火药粒(约占药盒体积的2%),绝大部分为圆柱形的模拟发射药粒,其尺寸为φ8 mm×13 mm。试验时,利用机械能量点燃模块装药中心传火管内附着的点火药包,点火药燃烧产生高温高压燃气使得靠近传火管的发射药首先被点燃,而后混合燃气不断扩散,使得模块药盒内真火药颗粒被点燃。过程中由于模块药盒内压力不断上升,与邻接药室自由空间形成较大压力梯度,达到破口压力后,燃气和假火药会以较大速度向药室右侧密闭端运动。求解时使用压力求解器,压力-速度耦合采用SIMPLE 模式,以实现动量、能量等参数的传递。由于气相与颗粒相耦合问题中,CFD 网格尺寸必须大于颗粒尺寸,故取网格尺寸为 15 mm,共计4 445个网格单元,并经过网格无关性验证。

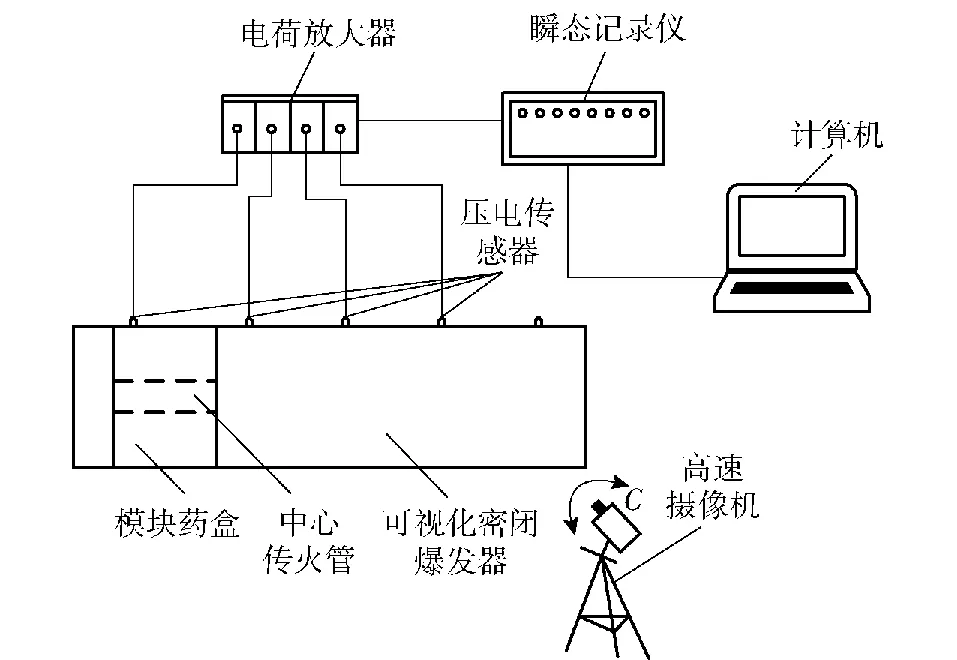
图5 试验装置示意图Fig.5 Schematic diagram of experimental devices

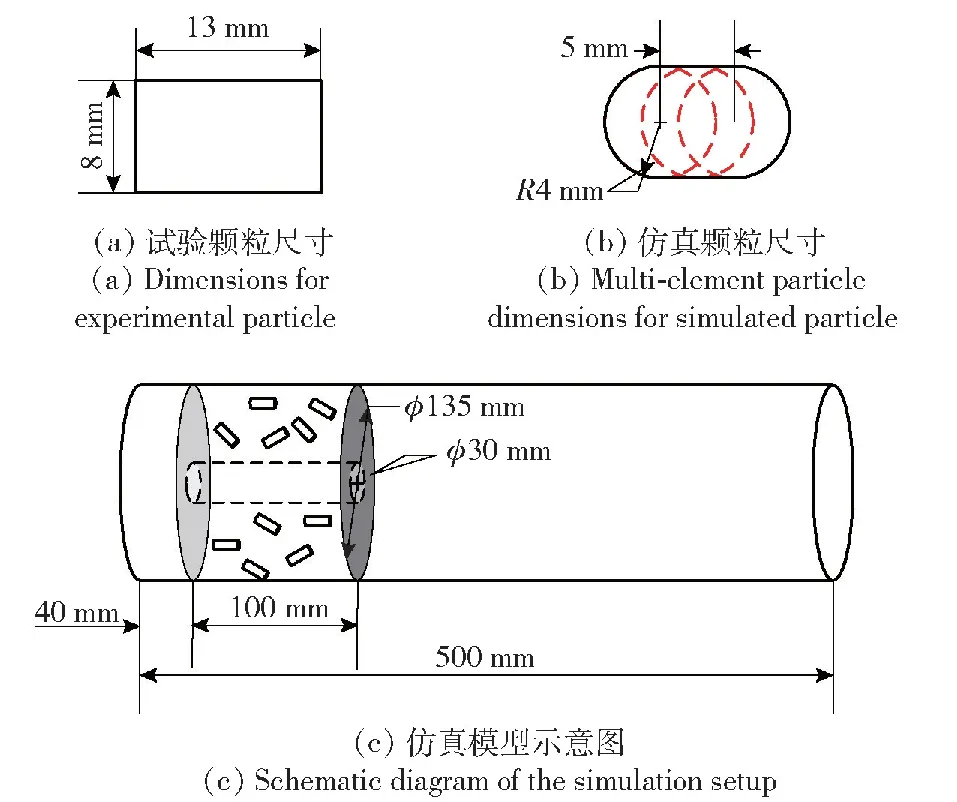
图6 计算模型结构示意图和柱状颗粒模型示意图Fig.6 Geometry of the calculation model and the cylindrical pellet model

图7为高速摄像机拍摄的药室内药粒在1 000 ms时的堆积形态,可看出药粒呈坡状集中分布于 350～475 mm区域[20]。为定量描述火药堆积形态,在X分别取350 mm、375 mm、400 mm、425 mm、450 mm、475 mm,Y=0 mm处分别测量药粒的高度。

图7 1 000 ms时刻模块装药点传火试验序列图[20]Fig.7 Sequence diagram of the modular charge’s ignition and flame-spreading experiment at 1 000 ms[20]

图8为数值计算得到的终态药粒分布的正视图,与试验所取特征点相对应,对终态药粒坡状堆积表面取6个点进行测量。将试验值与数值计算值相比较,如图9所示,发现数值模拟与试验测量值的平均误差约为4.9%,远小于试验估计的测量误差15%,并且与采用等体积球形颗粒的模拟仿真相比,一定程度上缩小了误差值,进一步表明颗粒的形状对颗粒行为具有很大影响,建立的类圆柱形颗粒离散单元模型对模拟单模块装药点传火过程中的药粒分布形态具有较高的精度。

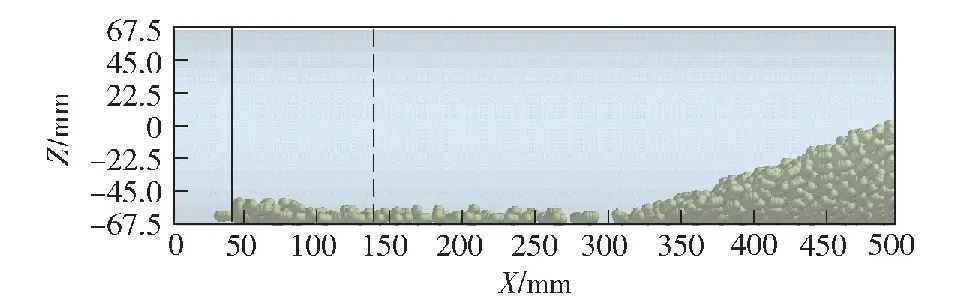
图8 终态药粒分布正视图(l0=40 mm)Fig.8 Front view of propellant pellets’ final distribution (l0=40 mm)

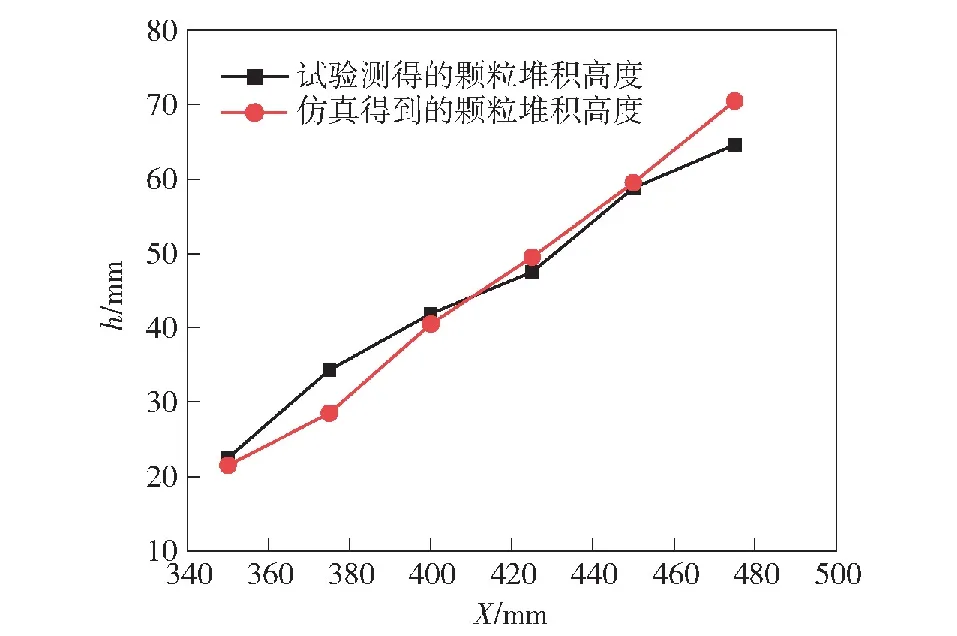
图9 药粒堆积高度的试验值与数值模拟计算值Fig.9 Exprimental and numerical values of propellant pellets’ stacking height

3.2 仿真结果与分析

图10为0.23～10 ms时药室Z=0 mm截面的气相压力云图。由图10(a)可知,在药盒破口前,中心传火管内附着的点火药包被点燃,经传火孔向药盒内输送高温高压燃气,模块药盒压力快速上升,约0.23 ms即由1大气压强上升至10 MPa;同时火药燃气也通过传火管端口向药室输入,但由于右侧药室相比模块药盒体积更大,故与模块药盒内压力相比压力上升速度较缓。当药盒内压力上升至约 10 MPa 时,假设药盒右端盖全部破开,由于此时模块药盒内颗粒密集,相间阻力大,火药燃气难以渗透,装药和药室自由空间邻接处形成较大压力梯度,如图10(b)所示,使得燃气和药粒混合物从模块药盒右端盖泄出。如图10(c)～图10(f)所示,当点火药和少量发射药粒燃烧完全后,药室内压差逐渐减小,最大压力不再升高。

为更好地理解和研究单模块装药点传火过程中的药粒运动特性,图11给出了仿真过程中0.23～600 ms 内药粒速度分布及飞散形态。如图11(a)所示,点火药燃烧产生的高压燃气经由传火孔向模块药盒内输入,在燃气射流作用下盒内颗粒获得速度,且越靠近传火管壁颗粒速度越大。0.23 ms 时药盒右端盖瞬时完全破裂,此时端盖两侧最大压差约为 9.6 MPa,大部分药粒和气体混合在一起加速向药室右侧运动。1.5 ms 时颗粒加速到最大值74.8 m/s,并且颗粒由于速度不同在药室内沿身管轴向呈环形分层分布。如图11(c)所示,6 ms时加速最快即速度分层最右侧的部分药粒最先与右侧密闭端固壁产生碰撞,速度迅速减小并且部分颗粒获得反向速度。此后,由于点火药和发射药的混合高压燃气不再生成,药室内的压力梯度逐渐减小,药粒向右的运动趋势不变,但速度在碰撞过程中减小。如图11(h)所示,火药颗粒600 ms时最大速度已小于0.5 m/s,且运动颗粒仅占2%左右,药粒整体趋于静止,故将该时刻近似作为药粒在药室内飞散运动的终止时间,此时的药粒分布形态视为最终形态。

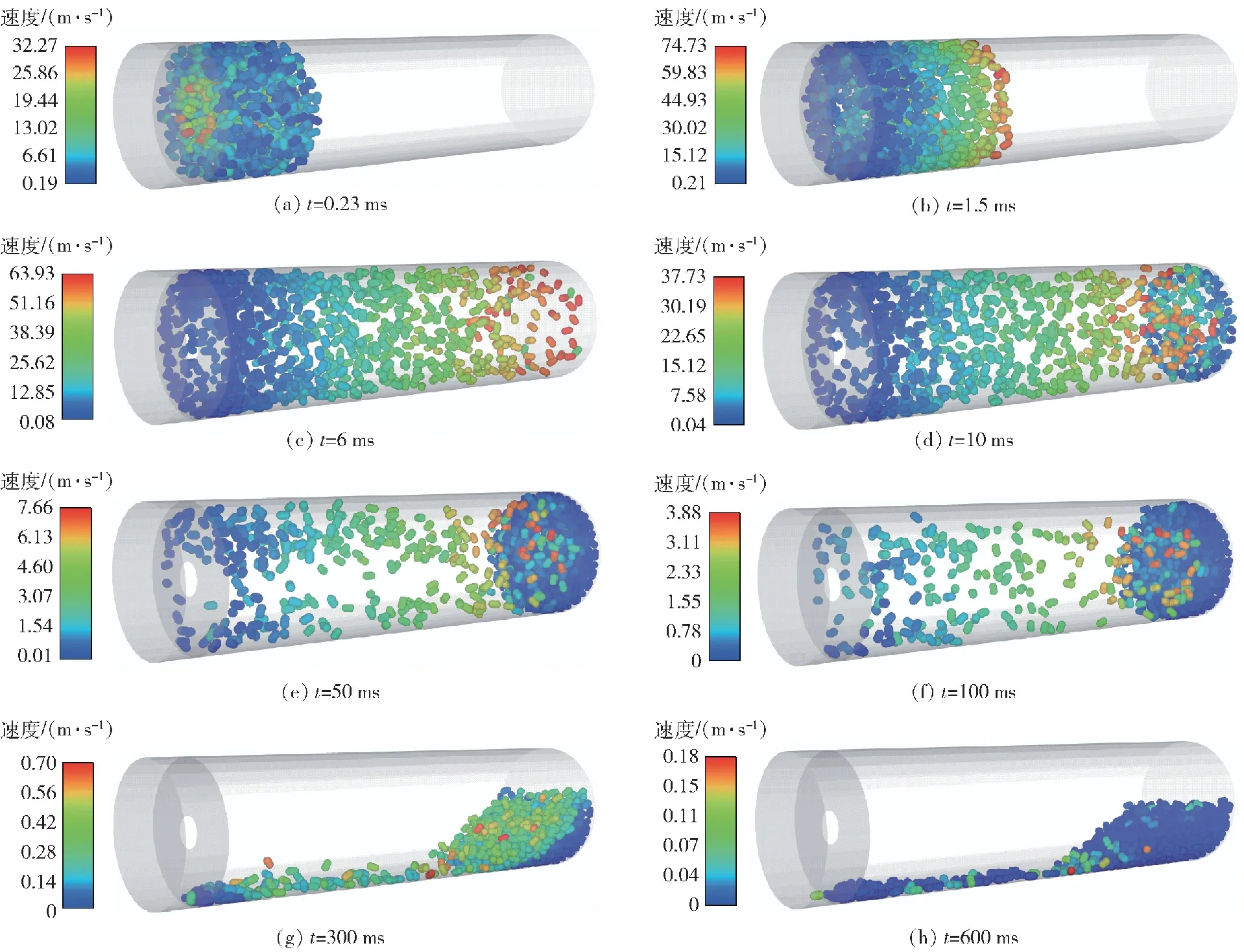
图11 不同时刻药室内的药粒速度分布及飞散形态Fig.11 Velocity and distribution of propellant pellets in the chamber at different moments

3.3 模块装填的位置对药粒分布形态的影响

为研究模块装填的初始位置对药粒分布形态的影响,如图12所示,将模块初始装填位置分别设置为距底火端10 mm、40 mm、70 mm和100 mm,数值模拟以上4种工况下单模块装药药盒破裂后药粒飞散运动。由图12可以看出,4种工况下药室内终态药粒从底火端向密闭端依次呈水平堆积和坡状堆积形态。为更好地对药粒堆积形态进行量化比较,引入了水平堆积轴向长度L和坡状堆积坡度角α两个特征参数,L表示沿药室身管轴向水平堆积起点到坡状堆积起点的距离,α则表示坡状堆积斜坡表面与水平面的夹角。分别对以上4种工况下终态药粒堆积表面进行L和α的测量,详细数据如表1所示。

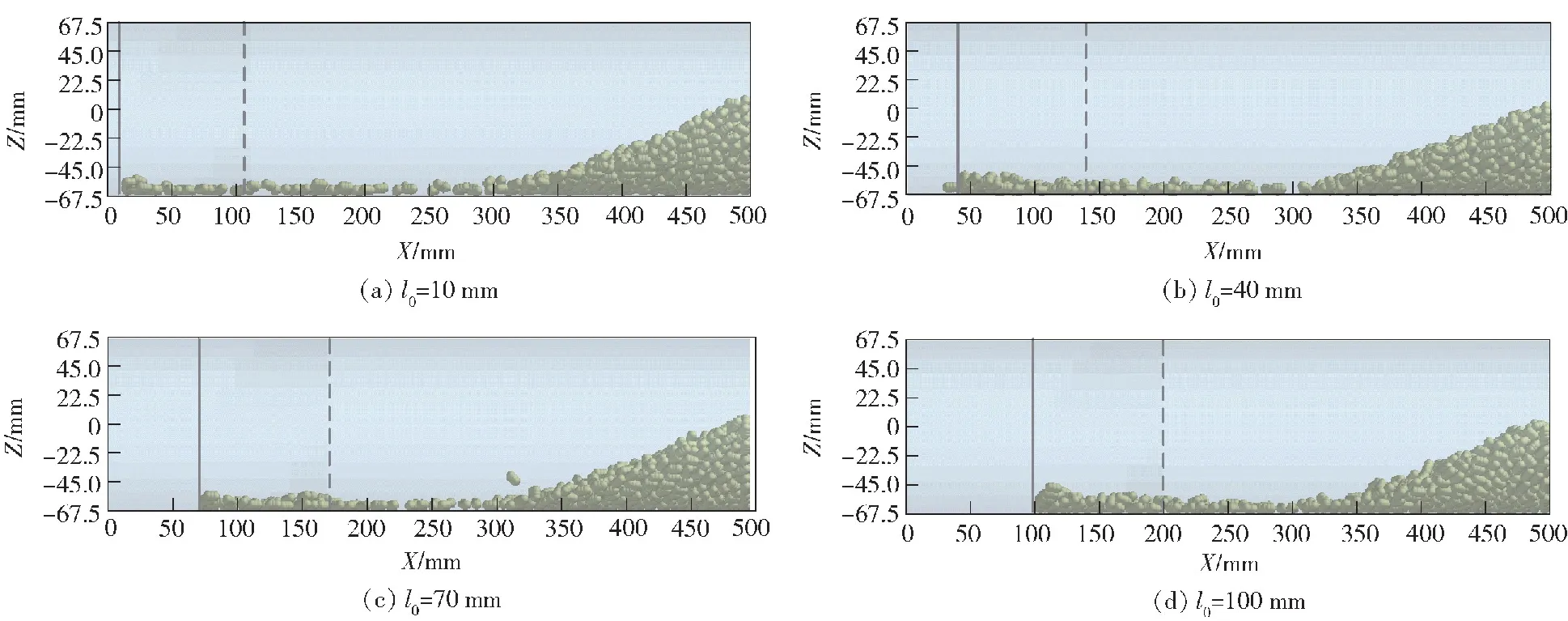
图12 不同装填位置下的终态药粒堆积分布Fig.12 Distribution of pellets under different working conditions

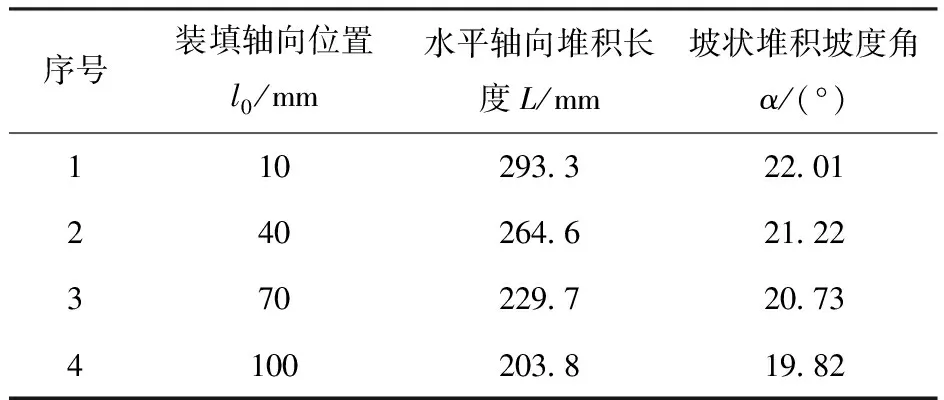
表1 药粒堆积特征参数

通过比较这两种特征参数在4种工况下的变化,可以看出随着模块药盒与药室底火端的距离增大,水平堆积轴向长度减小,坡状堆积变平缓,坡度角减小。由图13可以看出,水平堆积轴向长度L随着模块药盒装填位置与底火端距离l0的增大线性缩短,其拟合公式为

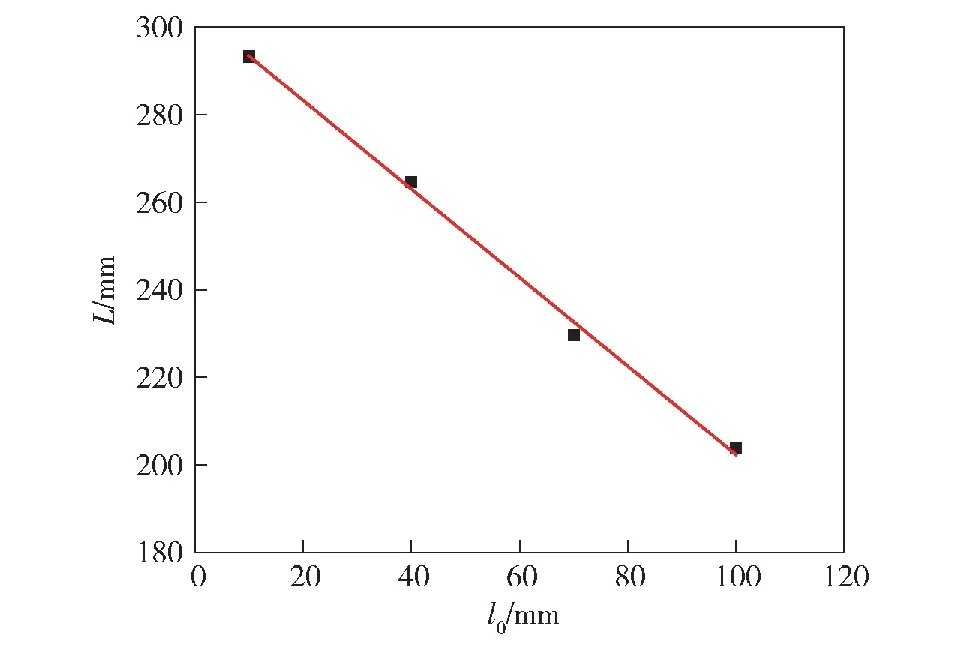
图13 水平堆积轴向长度与模块药盒装填轴向位置的关系Fig.13 Relationship between the axial length of the horizontal stacking of propellant pellets and the horizontal loading position of the modular cartridge

L=-1.011 3l0+303.473 3 (R2=0.995 61)

上述结果与陈安等[20]基于球形颗粒建立的模型所获得的颗粒堆积变化趋势一致,但与之相比,采用柱状颗粒模型仿真获得的药粒堆积特性参数变化更小。之所以出现上述情况,是因为模块药盒右端盖破裂瞬间,颗粒受到气相压强的作用,因为等体积球形颗粒垂直于压力梯度的投影大于大部分柱形颗粒(与压力梯度方向垂直或近似垂直的较少颗粒除外),球形颗粒获得更大的压力,故两种颗粒在相同质量下,球形颗粒将获得更大的加速度,柱状颗粒与之相比到达药室密闭端的速度更小,由图11(b)和图11(c)可知,颗粒最大速度约为74.73 m/s,到达右侧密闭端的速度约为64 m/s,而球形颗粒的最大速度可达93 m/s[20]。故在后面较小压强梯度下加速的颗粒距离药室右侧较远距离时速度就不再增加,使得终态颗粒分布较均匀,坡状堆积的坡度角较小。而随着模块药盒的装填位置右移,水平堆积轴向长度缩短,主要原因是模块药盒破裂时仅右端盖全部破开,颗粒在气相压力的作用下向右运动,水平堆积起始位置向右移动;颗粒堆积坡度减小则是因为随着模块药盒与药室底火端的距离增大,颗粒到达药室右壁面的距离减小、速度增大,无论是颗粒-壁面还是颗粒-颗粒发生碰撞后,将获得更大的反向速度,药粒将反向运动更远的距离后落下,散布更均匀,使得坡状堆积角变小,但由于距离变化较小对颗粒速影响比较小,这种变化也不是很明显。