改进的基于奇异值分解的图卷积网络防御方法

金柯君，于洪涛，吴翼腾，李邵梅，张建朋，郑洪浩

（信息工程大学，郑州 450001）

0 引言

图（Graph）在表示现实中的各类关系中具有独特的优势，已经成为数据挖掘和机器学习领域的重要研究对象。图神经网络（Graph Neural Network，GNN）是获取图节点和关系特征的有效工具之一［1］，具有良好的性能，被广泛应用于各项图分析任务，例如：节点分类［2］、链路预测［3］、图分类［4］、社区检测［5］等，图神经网络在图表示学习领域取得了较大成功。然而研究表明：图神经网络在面对专门设计的对抗性攻击时存在鲁棒性差的问题［6］。攻击者可以通过操纵图结构或节点属性“欺骗”图神经网络，从而生成图对抗性攻击。在金融系统和风险管理等安全攸关的领域应用中，图神经网络的这一安全缺陷引发了研究者的高度关注。例如，在信用评分系统中，欺诈者可以伪造出与一些高信用客户的连接，从而逃避基于图神经网络的反欺诈模型的检测。因此需要针对图神经网络对抗性攻击问题研究行之有效的图神经网络防御方法。

对抗性攻击根据攻击阶段不同分为污染测试数据的逃逸攻击和污染训练数据的投毒攻击［7-9］。本文主要研究针对图卷积网络（Graph Convolutional Network，GCN）投毒攻击的防御方法。在投毒攻击场景下，图数据在模型训练之前已被扰动，因此针对图投毒攻击常用的防御方法是在模型训练之前对图数据作净化处理，清洗污染后的训练数据以降低攻击的影响，从而保证训练得到模型的准确性。防御方法的关键问题是如何净化被污染图的训练数据。

研究表明，现实世界中的图具有一些共同性质［10］。首先，这些图都具有低秩性和稀疏性，例如，在社交网络中大多数人只与少数节点连接，并且影响用户之间连接的因素较少［11］；其次，图中相连接的节点往往具有相似的特征或属性（称之为特征平滑性）［12］，例如，在引文网络中，具有引用关系的两个出版物通常具有相似的主题［13］。实验研究表明，对抗性投毒攻击中修改边的有效性强于修改特征，且增加边的攻击性强于删除边，增加连边会增大邻接矩阵的秩［14］，破坏原图的低秩性和稀疏性；并且对抗性攻击倾向于在节点特征明显不同的节点之间添加连边［8］，破坏原图的特征平滑性。

为了净化攻击后的图数据，Entezari 等［14］提出了奇异值分解（Singular Value Decomposition，SVD）的预处理方法，对扰动后的图进行奇异值分解和低秩近似处理，保证低秩性以抵御攻击。然而该预处理方法只考虑图的低秩性，忽略了图的特征平滑性等其他规律，对精心设计的对抗性攻击的防御效果有待提升。本文提出了一种改进的基于奇异值分解的图卷积网络防御方法ISVDatt，使图卷积网络保持低秩性和特征平滑性等性质。具体而言，在SVD 之前，先进行一轮预处理，筛选出节点特征明显不同的节点之间的边并删除；再进行奇异值分解和低秩近似等操作，实现对污染图数据的净化，之后再用于图卷积网络模型的训练。在图深度学习常用的数据集上进行了大量实验，结果表明ISVDatt 能够有效地防御针对图结构的投毒攻击，相较于基于SVD 的防御方法，具有更佳的防御效果，并且复杂度较低，具有较高的实用价值。

1 相关工作

1.1 图和图卷积网络的定义

图是一种关系型结构数据，定义为G(V，E)，其中：V={v1，v2，…，vN}表示节点集合，E={e1，e2，…，eM}表示连边集合，N和M分别表示图中节点和边的数量。图中节点之间的连接关系通过邻接矩阵A表示，在无权无向图中，A={0，1}N×N，AT=A；当节点vi和节点vj存在直 接连边 时，Ai，j=1，否则Ai，j=0。特征图中每个节点有d维的特征向量，节点特征矩阵用X∈{0，1}N×d表示。节点分类任务是图上的基准测试任务之一［15］。假设每个节点vi有特征向量xi和标签yi相关联，节点分类的目的是利用图G(V，E)和有标签节点的信息训练一个节点分类模型，并利用该模型正确预测无标签节点的类别。

传统深度学习模型难以直接处理图数据，以图卷积网络（GCN）为代表的图神经网络应运而生。Kpif 等［13］于2016 年提出了GCN，它为图数据的处理提供了一个崭新的思路，将深度学习中常用于图像的卷积神经网络应用到图数据上。GCN 通过图卷积层聚合周围节点的特征以更新自身节点。节点特征更新函数为：

1.2 图对抗性攻击

图对抗性攻击指的是攻击者通过对图数据的结构或节点特征进行微小的扰动，达到损害目标模型性能的目的［16］。在图对抗学习中，未被攻击的图称为原始图G，被攻击后的图称为扰动图，攻击算法添加或删除的边称为扰动边，修改图中的边会改变图的邻接矩阵，扰动图的邻接矩阵表示为，改变邻接矩阵的攻击算法称为拓扑攻击；如果攻击算法修改了图的特征矩阵，则扰动图的特征矩阵表示为，改变特征矩阵的攻击算法称为特征攻击。图对抗性攻击根据攻击的时机可以分为污染测试数据的逃逸攻击和污染训练数据的投毒攻击［7］。图对抗性攻击由Zügner 等［6］首次提出，他们提出了Nettack 算法，选择图中的单个节点，通过修改该节点的结构或特征改变模型对该节点的预测，采用贪婪算法逐节点进行扰动得到扰动图。之后，面向图神经网络的对抗攻击方法的研究相继展开，出现了快速梯度攻击（Fast Gradient Attack，FGA）［17］、Metattack［18］、GF-Attack（Graph Filter Attack）［19］、ReWatt［20］等多种图对抗性攻击方法。

1.3 图对抗性防御

随着图对抗性攻击带来的各种安全问题，提高GNN 的鲁棒性显得愈加重要，图对抗性防御工作已经开始得到关注和研究。图对抗性防御是指通过一定的策略，使GNN 模型即使受到对抗攻击，依旧能够得到正确的输出结果，从而保证模型鲁棒性［9］。当前，已经有多种防御算法用于提高GNN模型的鲁棒性［21］，如Dai 等［16］发现在训练中随机丢弃一些连边可提高应对攻击的鲁棒性。针对逃逸攻击，增强GNN 鲁棒性的方法主要包括攻击检测和对抗训练等，例如Feng等［22］提出了图对抗训练（Graph Adversarial Training，GAT）方法以及虚拟图对抗训练（Virtual Graph Adversarial Training，GATV）。而针对投毒攻击，目前多数防御算法采用修改模型的策略，出现了SVD［14］、鲁棒图卷积网络（Robust Graph Convolutional Network，RGCN）［23］、Pro-GNN［24］等防御策略。这些方法可以有效防御针对模型训练阶段的投毒攻击。

表1 列举了上文提到的常见的图对抗性攻击与防御方法，本文主要研究针对投毒攻击的图对抗性防御，投毒攻击将扰动样本添加到训练数据中，一个自然的想法便是采用图净化处理，清洗过滤掉图中被污染的数据。基于此，本文提出了ISVDatt。

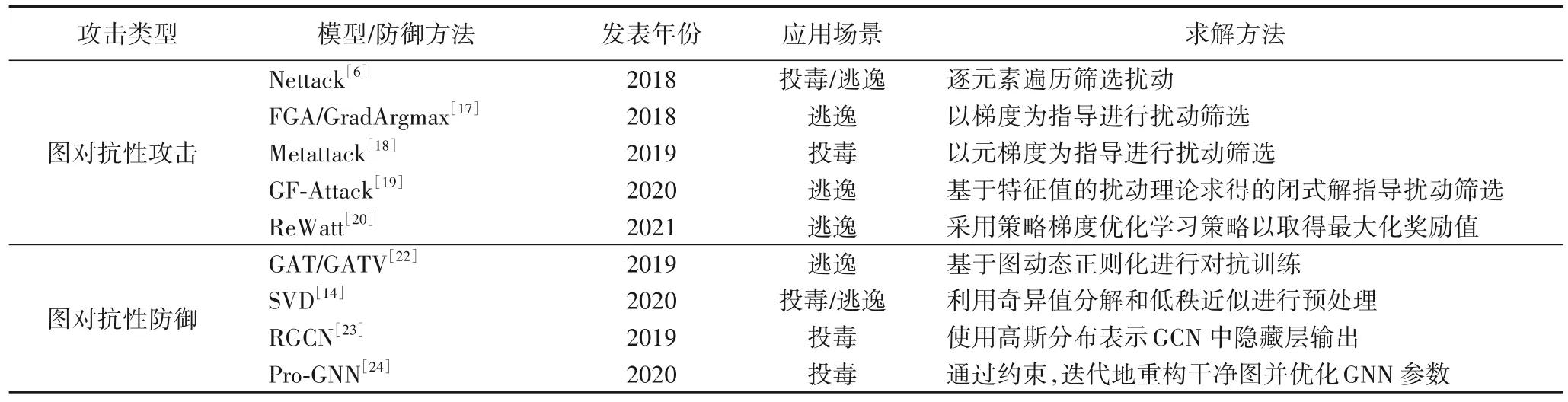
表1 常见图对抗性攻击与防御方法Tab.1 Common graph adversarial attacks and defense methods

2 本文方法

2.1 研究动机

Entezari 等［14］研究发现对抗性攻击会扰动图结构，从而增加邻接矩阵的秩，并提出了基于奇异值分解（SVD）的预处理方法以消除加入图结构的对抗性扰动（该防御方法简记为SVD）。尽管该方法在一定程度上可以达到防御效果，但基于SVD 的预处理方法仅考虑到原始图的低秩性遭到破坏，防御效果仍有改进空间。

根据1.1 节分析，GCN 模型基于特征平滑性假设而设计，如式（1）所示，模型的主要原理是图卷积层的特征聚合操作汇聚了与某节点关联的其他节点特征，使得经GCN 处理的节点特征也具备特征平滑性。本文认为，GCN 模型的脆弱性也表现在图卷积层的特征聚合操作：对抗性攻击通过增加虚假连边得到扰动图，扰动图破坏了原始图中节点的特征平滑性；GCN 模型会被扰动图干扰，使得经图卷积层聚合的节点特征不再具备原始图的特征平滑性，导致预测错误。因此，保持图中节点之间的特征平滑性可有效提高GCN 的鲁棒性。

基于这个假设，本文提出一种针对图卷积网络投毒攻击的净化防御方法ISVDatt，旨在对图数据进行净化处理，使图保持节点特征平滑性和低秩性。先筛选扰动图特征明显不同节点之间的边并删除，保证特征平滑性；再进行奇异值分解和低秩近似处理，保证邻接矩阵的低秩性，处理后的图可用于GCN 模型的训练。

2.2 目标模型

研究表明，2 层的GCN 模型在节点分类中性能表现较好。为了说明本文提出的防御方法的有效性，以2 层GCN 模型完成节点分类任务为例，公式表达如下：

其中：A为邻接矩阵；X为节点特征矩阵；W1和W2分别为输入层到隐藏层、隐藏层到输出层的训练参数矩阵；为模型输出；Y为节点的真实标签；使用交叉熵损失函数，可得到损失函数计算公式。GCN 模型训练阶段损失函数如下：

2.3 算法框架

ISVDatt 的框架如图1 所示，在模型遭受投毒攻击以后，该方法对扰动后的邻接矩阵进行图净化处理，处理后再用于GCN 模型的训练。具体而言，ISVDatt 方法主要分为2 个步骤：

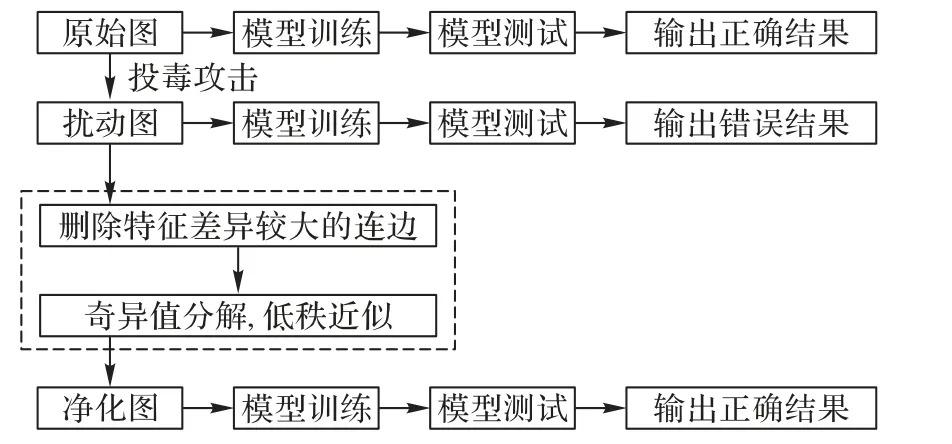
图1 ISVDatt方法框架Fig.1 Framework of ISVDatt method

1）删除特征差异较大连边。采用杰卡德相似系数［25］作为评分函数对扰动后的邻接矩阵的节点特征之间的相似度进行度量，并删除特征相似度较低的连边，即具有明显不同特征的节点之间的连边，再进行下一步处理。

2）奇异值分解、低秩近似处理。对第一步处理后的邻接矩阵进行奇异值分解，再使用最大的k个奇异值重组矩阵实现低秩近似处理。完成了对污染图数据的净化后，再使用处理后的图训练GCN 模型。

2.3.1 删除特征差异较大连边处理

Dai 等［16］简要介绍了一种低成本的防御方法，该方法通过删除部分连边，能略微提高模型应对攻击的鲁棒性。对抗性攻击倾向于在节点特征明显不同的节点之间添加边，除去这类边就可有效净化污染数据。基于这个假设，本文提出的ISVDatt 在扰动后的邻接矩阵中，筛选出特征差异较大的节点之间的边并移除。

本文研究的GCN 中，每个节点具有d维二元特征，特征为0 或1，采用杰卡德相似系数来评估节点之间的特征相似度，可得到特征相似度矩阵J。根据文献［26］，在二元离散条件下，节点vi和节点vj的杰卡德相似系数定义如下：

其中：M11表示节点vi的特征为1、节点vj的特征也为1 的数量；M01表示节点vi的特征为0、节点vj中特征为1 的数量；M10表示节点vi的特征为1、节点vj的特征为0 的数量。Ji，j∈[0，1]，Ji，j值越大说明节点vi和节点vj的相似度越高。

在式（4）特征相似度计算的基础上，对扰动后的邻接矩阵进行预处理，筛选出特征差异较大的节点之间的边并移除。尽管干净的图也可能有少量这样的边，但数量极少，删除这些边对目标节点的预测几乎没有影响，甚至能改善结果。定义Di，j为删除连边矩阵操作：

其中：τ为界定特征相似度的阈值，将受到攻击后模型的邻接矩阵记为={0，1}N×N，经过该处理后的邻接矩阵可以过滤部分扰动数据，记为A＇={0，1}N×N。

2.3.2 奇异值分解和低秩近似处理

奇异值分解（SVD）是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统、自然语言处理等领域，是很多机器学习算法的基石［27］。在上述删除特征差异较大连边的处理后，再对处理后的邻接矩阵进行奇异值分解和低秩近似处理，使其保持图的低秩性。奇异值分解定义如下：

其中：Σ为N阶对角矩阵，它的对角线上的元素σi为奇异值，并且σ1＞σ2＞… ＞σmin，σi可由A＇TA＇的特征值λi取平方根求得，矩阵A＇的秩即为非零奇异值的个数；矩阵U和V都为N阶正交矩阵，U的列元素称为左奇异向量，由A＇A＇T的特征向量组成，V的列元素称为右奇异向量，由A＇TA＇的特征向量组成，本文研究无向图，A＇T=A＇。式（7）可以写成：

经过奇异值分解后，再对矩阵A＇进行低秩近似操作，先在矩阵Σ中保留最大的k个奇异值，将剩余奇异值置0，再结合对应的左右奇异向量便可近似描述矩阵A＇，即

经过式（9）低秩近似处理后的邻接矩阵记为A″，为N阶矩阵，它的秩为k。至此，攻击后的邻接矩阵已过滤大量杂质，可直接用于GCN 模型的训练。

2.4 ISVDatt的实现

ISVDatt的主要步骤为：

1）根据式（4）计算特征相似度矩阵J；

2）根据式（5）获得过滤图邻接矩阵；

3）根据式（8）进行奇异值分解处理；

4）根据式（9）进行低秩近似，采用前k个奇异值重构矩阵A″。

具体算法伪代码如下所示：

算法 改进的基于SVD 的图卷积网络防御方法ISVDatt。

3 实验与结果分析

3.1 实验设置

3.1.1 实验环境

本文实验环境为：型号为TITAN Xp 的GPU 显卡，运行环境 ubuntu16.04 系 统，CUDA10.0，Python3.7 以 及PyTorch1.2.0。

3.1.2 数据集及评价指标

本实验采用图深度学习常用的具有节点特征的Citeseer［28］、Cora［29］、Pubmed［30］数据集，表2 列出了这些数据集的统计特征。数据集随机划分为标记节点和未标记节点两部分，其中：标记节点全部用于训练（占比10%）；在未标记的节点中，一部分用于测试（占比80%），另一部分用于验证（占比10%）。

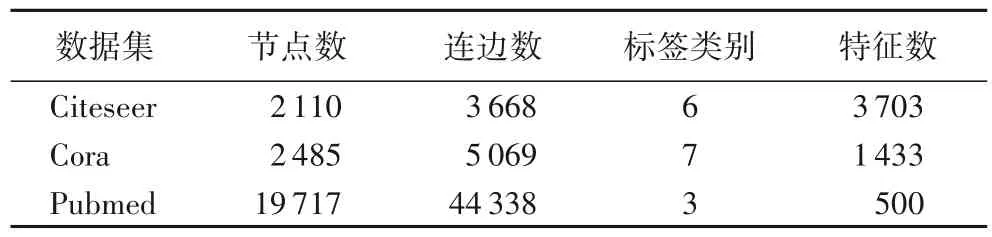
表2 数据集统计特征Tab.2 Statistical characteristics of datasets

本章每轮实验均进行10 次并记录平均值，使用模型的分类准确率作为评价指标，评估防御方法的有效性主要对比2 项内容：

1）在原始图上，需要保持GCN 原模型的性能；

2）在扰动图上，尽可能地提高对对抗性攻击的防御效果。

3.1.3 攻击方法

本实验采用经典的对抗性攻击算法：Metattack 算法［18］和DICE（Delete Internally，Connect Externally）启发式算法［31］，攻击方法对图卷积网络的连边进行扰动，将扰动连边数与连边总数的比值称作扰动比例。下面对这两种攻击算法进行简要介绍：

1）Metattack 攻击使用元学习中的元梯度方法解决投毒攻击的双层优化问题，先计算元梯度以指导攻击行为，之后采用贪婪算法对邻接矩阵遍历扰动以实现攻击。

2）DICE 启发式算法则根据“从同类节点中删除连边，在不同类节点间增加连边”这一规则，利用启发式算法，删除部分连边，随后通过添加连边恢复其影响力。

3.2 消融实验

3.2.1 防御模型构建

本文的防御方法ISVDatt 在SVD 的基础上增加了删除特征差异较大连边的操作，使图同时保持低秩性和特征平滑性，因此防御模型主要由删除特征差异较大连边、奇异值分解和低秩近似两部分组成，按照操作顺序不同分别建模如下：

1）先进行奇异值分解和低秩近似，再删除特征差异较大连边，模型记为ISVD_0。

2）先删除特征差异较大连边，再进行奇异值分解和低秩近似，即本文方法，模型记为ISVDatt。

以Cora 数据集为例（其他数据集上均能得到相似结果），分别在原始图和扰动图上进行实验，扰动图选择Metattack 攻击5%至25%的连边，节点特征相似度阈值τ和低秩近似后的矩阵秩k分别取为0.05 和10。分别记录不采用防御方法（GCN）和采用ISVD_0 与ISVDatt 的2 种防御模型后的分类准确率，结果如表3 所示。

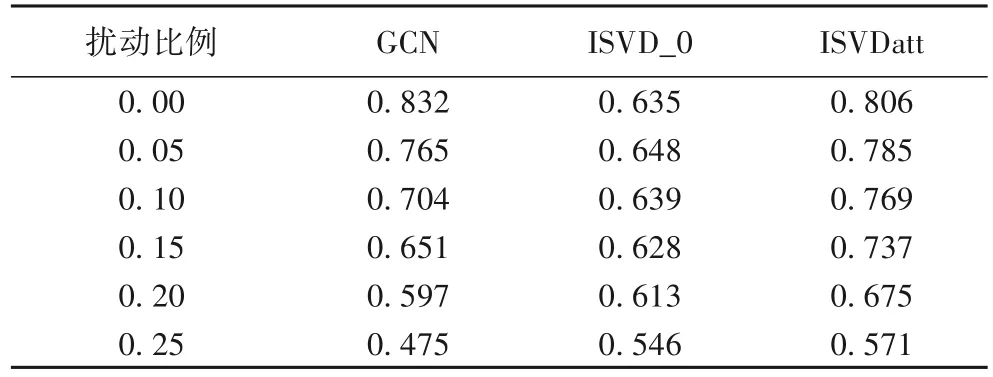
表3 不同模型配置在Cora数据集上的分类准确率Tab.3 Classification accuracy of different models under different settings on Cora dataset

如表3 所示，对于原始图（扰动比例为0），采用模型ISVDatt 和ISVD_0 后，分类准确率均下降，ISVD_0 下降幅度较大，ISVDatt 幅度较小，说明这2 种模型对于未受干扰的原始图的性能均有影响，但ISVDatt 模型对原始图影响较小。对于Metattack 攻击下的扰动图，采取ISVDatt 模型防御后，分类准确率提升明显，达到了一定的防御效果；而采用ISVD_0模型后，在扰动比例较小时，模型的分类准确率不升反降，扰动比例为20%时，才有所提升，但幅度较小。综上，ISVD_0模型防御效果不如ISVDatt。究其原因，ISVD_0 模型先采用奇异值分解和低秩近似，后删除特征差异较大连边，奇异值分解和低秩近似本质是对邻接矩阵进行降秩，对其蕴含的连边信息进行了压缩处理，常应用于图像处理方面，然而图数据的节点之间存在联系，该操作会在一定程度上破坏节点的连边情况，处理后的邻接矩阵未必能反映原图真实的连接情况，影响下步操作中杰卡德相似系数对特征差异较大连边的判定，导致删除连边操作随机性较大。因此ISVD_0 模型防御效果较差。

反观ISVDatt 模型，先采用删除特征差异较大连边操作，该操作过滤明显的可疑连边，几乎不会误删正常连边，为下一步操作作了铺垫，提高了奇异值分解的准确性，取得了更好的防御效果。故最终本文提出的防御方法采取先删除特征差异较大连边、后奇异值分解的模型框架（如图1 所示）。

3.2.2 防御参数选择

本文防御方法的性能与参数设置相关，防御过程主要由删除特征差异较大连边与奇异值分解与低秩近似2 个阶段组成，这2 阶段的关键参数（即节点特征相似度阈值τ和低秩近似后的矩阵秩k）具有一定实际意义，其中节点特征相似度阈值τ决定删除连边的数量，净化后矩阵秩k则衡量低秩近似的程度。本节对ISVDatt 的这2 个阶段的关键参数设置进行分析。通过控制变量法，以Cora 数据集为例进行实验。

本节实验分别在扰动图和原始图上分别进行测试，其中扰动图选择Metattack 攻击方法扰动10%的连边。节点特征相似度阈值τ设置为：0～0.25，步长为0.05；低秩近似后的矩阵秩k设置为5～25，步长为5。结果如表4 所示。

由表4 可知，随着节点特征相似度阈值τ增大，删除连边增多，同时对原始图的影响也增大；净化后矩阵秩k若过大则过滤污染数据较少，若k过小则对原始图影响较大。为提高模型的分类准确率，参数需要选择合适的值。根据上图结果，综合考虑参数变化在扰动图和原始图上的影响，力求在扰动图上获得较好的防御效果和对原始图影响较小，最终设置τ为0.05，k为10，可以在保持原矩阵特性的基础上消除大部分扰动数据。

3.3 防御效果实验

为了验证ISVDatt 的有效性，本文将它与针对GCN 投毒攻击的其他三种防御方法进行比较，分别为：

1）Pro_GNN［24］：按照图的特性，从受扰动的图和模型参数中学习原始图拓扑结构和鲁棒性，迭代地重构1 个新图以防御对抗性攻击。

2）RGCN［23］：利用高斯分布对扰动的容忍性，将图卷积层的隐层节点表示为高斯分布以吸收对抗攻击带来的影响；此外还利用方差为邻居节点分配注意力权重，具有高方差的节点将受到惩罚。

3）SVD［14］：将受扰动的图进行SVD，低秩近似对图数据重组。

3.3.1 在原始图上的分类性能

本节在GCN 模型上对各防御方法进行测试，结果如表5所示。由表5 可知，在未受扰动的原始图上采用以上4 种防御方法后，模型的分类准确率变化较小，仍能保持原本的性能。

表5 不同防御方法在原始图上的分类准确率Tab.5 Classification accuracy of different defense methods on original graph

3.3.2 在扰动图上的分类性能

本节分别采用了Metattack 和DICE 对GCN 进行攻击，扰动比例从0 增至25%，分别记录不采用防御方法和采用防御方法后模型的节点分类准确率。实验的结果如表6 所示。由表6 实验结果可知，相较于RGCN 和SVD，本文提出的ISVDatt 多数情况下分类准确率更高，具有更好的防御效果。原因是RGCN 采用高斯分布作为GCN 层间节点的潜在表示，因此当图中具有较多扰动边时防御性能不佳；SVD 对图进行了简单的净化处理，具有局限性，比如在DICE 攻击下，SVD防御效果较差，原因是DICE 攻击具有较高的随机性，SVD 操作过于简单，因此防御效果一般；ISVDatt 在SVD 基础上增加了删除特征差异较大连边的操作，进一步净化污染数据，提高了模型应对对抗性攻击的鲁棒性。但ISVDatt 防御性能不如Pro_GNN，因为Pro_GNN 方法将图视作超参数，反复迭代调优。尽管Pro_GNN 具有较好的防御效果，但需要同时满足图的多项特性指标，模型性能对超参数的改进较为敏感，计算过程较复杂，计算资源消耗较大；而ISVDatt 相较于Pro_GNN 复杂度较低，时间开销可以忽略不计，在3 个数据集的GCN 模型上启用防御仅使训练运行时间增加了不到20 s。综合考虑到时间成本和运算复杂度，ISVDatt 比Pro_GNN 更具优势。ISVDatt 作为一种对扰动图进行净化的方法，可以应用于多种场景，具有较高的防御通用性。

表6 Metattack和DICE攻击下的分类准确率Tab.6 Classification accuracies under Metattack and DICE attacks

4 结语

图对抗性攻击倾向于在特征明显不同的节点之间添加连边，以破坏图的稀疏性和特征平滑性等特性。根据该结论，本文提出了一种改进的基于奇异值分解的图卷积网络防御方法ISVDatt。该方法可以在模型遭受投毒攻击后对中毒数据进行预处理，达到数据净化的效果，从而提高GCN 模型应对对抗性攻击的鲁棒性。本文在图深度学习常用的3 个开源数据集Citeseer、Cora 和Pubmed 上进行大量实验，验证了本方法具有较好的防御效果。但是在实验中发现，该方法对训练数据进行了净化处理，改变了图结构，在未受投毒攻击的原始图上采取该防御方法会略微降低GCN 模型的分类准确率。因此在未来的工作中，我们将致力于改善运用本方法在原始图上的性能，并进一步降低对抗性攻击带来的影响，提高GCN 模型应对对抗性攻击的防御能力。