基于判别性矩阵分解的多标签跨模态哈希检索

谭 钰，王小琴，蓝如师*，刘振丙，罗笑南

（1.广西图像图形与智能处理重点实验室（桂林电子科技大学），广西 桂林 541004；2.卫星导航定位与位置服务国家地方联合工程研究中心（桂林电子科技大学），广西 桂林 541004）

0 引言

随着多媒体数据数量和种类的快速增长，不同类型的检索数据为检索任务带来了新挑战，由此需要更有效的算法解决多样化跨模态检索问题。跨模态检索需要解决异构数据的表示及比较问题，如给定一个图像样本，如何有效且快速地检索出相关的文本、视频等其他模态数据。为获得更好的性能，跨模态检索引入了哈希学习方法［1-5］以降低存储成本并获得更快的检索速度。通常，跨模态哈希方法可分为两类：有监督方法［6-10］和无监督方法［11-15］。无监督方法旨在挖掘数据之间的结构关系；而有监督方法可以充分利用标签信息，在构建相似关系时获取更多的语义关系信息。

近些年来，一些现有的跨模态哈希方法［16-21］认为，可以通过协同矩阵分解将原始特征的语义关系保留在隐式子空间中。此外，部分哈希方法［22-27］对哈希向量的平衡性进行了研究，并认为哈希向量的平衡性可以最大化信息熵。

在现实场景中，多标签的检索样本占总检索样本的绝大部分，却很少有哈希方法关注构建多标签数据下的平衡哈希向量，并且丢弃了大部分的标签信息，导致哈希码的可信度和语义保持性降低。

为解决这些问题，本文提出一种简单而有效的哈希方法——判别性矩阵分解的多标签跨模态哈希（Discriminative Matrix Factorization Hashing，DMFH）。本文目标是通过矩阵分解获得具有模态特性的公共隐式子空间，并为成对的异构数据生成统一的哈希码。为使生成的哈希码更具判别性，本文进一步构造了一个可以精确度量数据关系的多标签相似矩阵。此外，本文还引入哈达玛矩阵以保持哈希向量的平衡状态。最后，通过量化子空间的数据表示获得目标哈希码。

1 相关研究

近些年来，协同矩阵分解（Collective Matrix Factorization，CMF）方法被应用于跨模态哈希检索中。CMF 旨在使用两个低秩矩阵的乘积来逼近一个非满秩的高阶矩阵。不同于传统跨模态哈希方法直接将数据投影到汉明空间，CMF 方法将数据投影到所分解出来的隐式子空间中。例如，协同矩阵分解哈希（Collective Matrix Factorization Hashing，CMFH）［21］方法首次将CMF 方法应用于跨模态检索领域，通过矩阵分解对原始特征进行分解并获得潜在隐式子空间，从而比较异构数据的相似性。Tang 等［18］通过CMF 得到隐式语义特征，并将原始空间的标签相似性与局部结构相似性保持到子空间中。Li 等［28］将核化特征进行矩阵分解，同时利用标签下的语义嵌入获取更优子空间，并将模态间和模态内的相似性保持于子空间中。Wang 等［29］首次将模态独立矩阵分解与模态联合矩阵分解融合：模态独立矩阵分解侧重于获取不同模态内特有的数据特征；模态联合矩阵分解侧重于获取不同模态间共有的数据特征。

在哈希学习中，二值码的质量是提升模型效果的关键。传统哈希方法通过模型最终获得的精度来评价所学哈希码的优劣，而模型的效果受多方面因素影响，由此对哈希码质量的判断并不准确。近些年来有研究人员对哈希码的质量作了进一步研究，Liu 等［22］通过哈希比特的平衡度与相似关系保持能力对哈希码的质量进行评价，认为好的二值码应当拥有平衡的二值占比，并证明了哈希比特的平衡性有助于保持原始数据的相似性关系。由此可知，平衡的哈希码能够携带更多的原始语义信息，有利于哈希学习获得更好的效果。此外，为了生成更具判别性的哈希码，Lin 等［24］将哈达玛矩阵引入哈希学习，利用哈达玛矩阵的每一行作为每个类的聚类中心，以最大化不同类别的差距。由于哈达玛矩阵为二值正交矩阵，每一行（列）在性质上与二值哈希码相同，且每一行（列）均为平衡向量，有利于生成更具平衡性的哈希码。

2 判别性矩阵分解哈希

2.1 符号及定义

2.2 方法描述

本文方法旨在利用CMF 方法获取到一个隐式子空间，以挖掘多模态数据之间的潜在关系。显然，若异构数据之间是语义相近的，它们在空间分布上也存在联系。有鉴于此，假设给定两个模态数据矩阵X和T，它们的矩阵分解可写作以下形式：

其中：UI∈Rp×d和UT∈Rq×d分别对应图像模态和文本模态的隐式向量矩阵；矩阵V∈Rd×n记录异构的成对数据在子空间中的统一表示形式。

检索时，需要将检索样本的原始特征投影到已获得的子空间中。为此，分别定义两个线性投影函数PI∈Rd×p和PT∈Rd×q，将图像和文本模态数据映射到子空间中。本文认为，具有相同标签的成对异构数据在子空间中拥有相同表示形式。基于这个思想，可通过式（2）实现异构模态数据X和T的子空间映射：

在单标签样本的情况下，传统的相似性矩阵构造方法仅通过异构数据之间是否有相同标签来判断相似性，但该方法在多标签样本检索中显得粗糙许多。区别于传统构造方法，针对多标签跨模态哈希检索问题，本文通过比较两个样本的共有标签占比来衡量样本间的相似程度，并构造出多标签样本下的相似性矩阵。对于两个样本xi和tj，相似性关系可以表示为以下形式：

其中：si，j∈[0，1]；N是数据xi拥有的标签总数。通过标签向量的内积计算得到两个样本共有的标签数，若两个样本完全不同，分子为0，则si，j=0；若两个样本相似，则si，j趋向于1，当共有标签达到xi拥有的标签总数时，认为两个样本一致。通常情况下，数据的相似性关系是相互的，相似性矩阵是对称矩阵。因此，在构造该相似性矩阵时，只对矩阵的上三角进行运算，即1 ≤i≤j≤n，矩阵的下三角部分通过si，j=sj，i得到。

本文方法认为，数据在子空间中的语义关系与数据在原始空间中的语义关系应当相近。因此，异构数据投影到子空间后的语义相似性损失写作以下形式：

为了保持多标签下向量的平衡性，本文方法引入2k阶哈达玛矩阵构造一个新颖的平衡矩阵C∈Rd×n，其中每一个ci都通过标签聚合的方式获得。更具体地说，哈达玛矩阵的每一行都可作为一个特定的类，通过计算d*=min{b|b=2k，m≤b，d≤b，k=1，2，3，…}获得哈达玛最短编码长度，最后执行函数hadamard（d*）构造出相应哈达玛矩阵。对于样本xi，需要从预构造的哈达玛矩阵中选择出对应的类向量，并将所有的类向量相加作为最终的平衡向量：

此后，为使目标哈希码具有平衡性，本文方法将式（5）构造出的平衡矩阵C替换式（4）中的一个子空间表示V。由此，式（4）可以被改写成：

2.3 目标函数

结合式（1）、（2）、（6），本文方法的总目标函数可以写作：

最后，通过量化子空间中的统一表示V得到目标哈希码B。

当输入值为正数时，二值函数sgn 的返回值为1，否则为-1。

基于上述方法，目标哈希码同时保留了异构数据的语义关系和平衡特性。

2.4 模型优化

由于矩阵变量V、PI、PT、UI和UT的存在，式（7）属于非凸优化问题，无法直接优化求解。但当任何一个变量是可变的，而其他变量是固定不变时，式（7）变成凸优化问题。因此，本文通过迭代优化的方式求解。求解步骤如下：

1）更新UI和UT。固定除UI和UT外其他变量，并移除无关项，式（7）可被改写为：

将式（9）、（10）对UI和UT的导数分别取为零，可以得到UI和UT的闭式解：

其中I∈Rd×d是单位矩阵。

2）更新PI和PT。固定其他变量并移除与PI和PT无关的项，式（7）可被改写为：

将式（13）、（14）中关于PI和PT的导数分别取为零，可以得到PI和PT的闭式解：

3）更新V。固定其他变量并将V的导数取为零，式（7）可以改写为：

具体算法流程如算法1 所示。

算法1 判别性矩阵分解的多标签跨模态哈希。

3 实验与结果分析

为验证本文方法的有效性，在两个文本-图像模态的多标签数据集MIRFlickr 和NUS-WIDE 上进行实验。实验采用平均精度均值（mean Average Precision，mAP）进行评估，并对比了几种最先进的跨模态哈希方法。

3.1 数据集

MIRFlickr 数据集由25 000 对图像-文本数据样本组成，来源于Flickr。每一个样本都为多标签数据，并属于规定的24 个种类其中一个或多个。在训练前，去除出现次数少于20 次的标签类别后剩下20 015 对数据；此外，去除缺失文本标签的样本，最终剩下16 738 对样本数据。划分出15 902 对样本作为训练集，836 对样本作为测试集。数据集中的图像样本由512 维的边缘直方图特征进行表示，文本样本由主成分分析（Principal Component Analysis，PCA）产生的500 维特征表示。在训练模型时，从训练集中随机抽取出5%的样本作为检索样本，其余样本作为训练集。

NUS-WIDE 数据集是源于Flickr 的真实场景数据集。完整的数据集包含269 648 对图像-文本样本，每个样本属于规定的81 个种类中的一个或多个。数据集中的图像样本由500 维的尺度不变特征变换（Scale-Invariant Feature Transform，SIFT）特征表示，文本样本由1 000 维的词袋特征表示。在实验前，对数据集的海量样本进行处理，筛选出属于最常见10 类的标签中的样本，得到大小为186 577 的成对数据集，并随机取出5%作为测试集，剩下部分作为训练集。

3.2 实验设置及对比方法

对于本文提出的方法，根据经验对实验中的参数进行以下的设置：λ=0.5，µ=1 000，γ=5 和e=500。在对比实验中，所有比较方法均运行了10 次，表中给出的所有数值都是平均性能的结果。此外，实验的二进制代码的长度设置在｛32，64，128｝的范围内，在配置3.4 GHz CPU、64 GB 内存的电脑和软件Matlab R2018b 上运行。

7 种先进的跨模态哈希方法包括：4 种基于CMF 的方法，即协同矩阵分解哈希（CMFH）算法［21］、有监督矩阵分解哈希（Supervised Matrix Factorization Hashing，SMFH）算法［18］、广义语义保持哈希（Generalized Semantic Preserving Hashing，GSePH）算 法［16］和联合与独立矩阵分解哈 希（Joint and Individual Matrix Factorization Hashing，JIMFH）算法［29］；以及3 种非CMF 的方法，即语义相关性最大化（Semantic Correlation Maximization，SCM）算 法［31］、判别性 二值哈 希（Discriminative binary Codes Hashing，DCH）方法［20］和子空间下语义标签哈希（Subspace Relation in semantic Labels for Cross-modal Hashing，SRLCH）算法［32］。特别说明，本文方法从NUS-WIDE 数据集的训练集中随机抽取15 000 个样本来训练本文提出的模型。

3.3 实验结果

实验部分分别完成了任务“以图搜文”（Image to Text，I2T）和“以文搜图”（Text to Image，T2I）的比较，结果如表1，加粗表示最优结果，下划线表示次优结果。由表1 可知，本文方法DMFH 在两个任务中均取得了最高的mAP。还可以看出，针对I2T 任务：

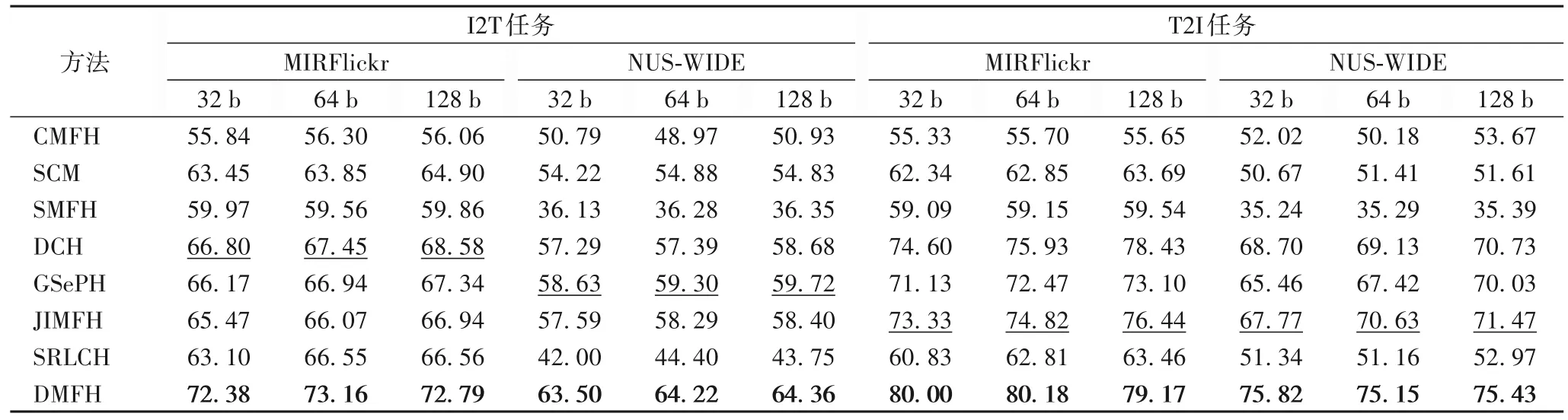
表1 I2T和T2I任务在实验数据集MIRFlickr和NUS-WIDE上的mAP对比 单位：%Tab.1 mAP results comparison for I2T and T2I tasks on experimental datasets MIRFlickr and NUS-WIDE unit：%

1）在MIRFlickr 数据集的实验中，对比使用简单方法构造相似性矩阵的方法GSePH，当二进制代码的长度分别为32 b、64 b 和128 b 时，本文方法的mAP 分别获得了6.21、6.22、5.45 个百分点的提升。这说明本文提出的多标签相似矩阵和平衡矩阵有助于学习到更具区分性的哈希码。

2）当二进制代码的长度分别为32 b、64 b 和128 b 时：在MIRFlickr 数据集的实验中，本文方法的mAP 比次优方法DCH 分别提高了5.58、5.71、4.21 个百分点；在NUS-WIDE数据集的实验中，本文方法的mAP 比次优方法GSePH 分别提高了4.87、4.92 和4.64 个百分点。

针对T2I 任务：

1）在MIRFlickr 和NUS-WIDE 数据集上，本文方法 的mAP 均高于I2T 任务的mAP，说明本文方法能够更有效地利用文本模态中的多标签语义信息，有助于提高T2I 任务的检索性能。

2）当二进制代码的长度分别为32 b、64 b 和128 b 时：在MIRFlickr 数据集上，本文方法的mAP 比次优方法JIMFH 分别提高了6.67、5.36、2.73 个百分点；在NUS-WIDE 数据集上，本文方法的mAP 比次优方法JIMFH 分别提高了8.05、4.52、3.96 个百分点。

3.4 讨论与分析

3.4.1 参数敏感性分析

为研究参数λ、µ和γ对模型的影响，本节对参数的敏感性作进一步的实验分析。在两个多标签数据集上，均使用长度为32 b 的哈希码进行参数λ和µ的实验；在模型训练时，依据实践经验设置正则项系数γ的值，并在所有实验中设定γ=5。

实验中设定参数λ的取值为｛0，0.1，0.3，…，1｝，实验结果如图1（a）、（b）所示。显而易见，两个数据集在λ=0.5 前后有较明显的波动。在I2T 任务中，NUS-WIDE 数据集在λ=0.5 达到峰值；在T2I 任务中，MIRFlickr 数据集λ=0.5 达到峰值。可以得出，在矩阵分解方法中，图像和文本两个模态的数据对子空间的生成有着近似等同的影响，两个模态的平衡有利于找到更优的子空间。

图1 实验综合分析曲线Fig.1 Comprehensive analysis curves of experiments

参数µ的实验取值范围为{10-3，10-2，10-1，…，103}，实验结果如图1（c）、（d）所示。对于数据集MIRFlickr 和NUSWIDE，当µ的取值越大，mAP 值趋于直线上升；对于数据集NUS-WIDE，当μ取值增大时，敏感性曲线较数据集MIRFlickr 更陡。结果表明，数据集越大对子空间与哈希投影近似程度越敏感；且哈希投影越接近所学习到的子空间，能够保留的相关性信息便越多，模型的效果越好。

3.4.2 收敛性分析

图2 展示了本文方法在最大的数据集NUS-WIDE 上的收敛曲线。可以观察到，随着训练时间的增加，本文方法能从初始值收敛到趋于不变，并且可以在20 次迭代时间内快速收敛，验证了本模型的有效收敛性。为此，在进行两个多标签数据集的训练中，均设置训练的迭代次数为20。

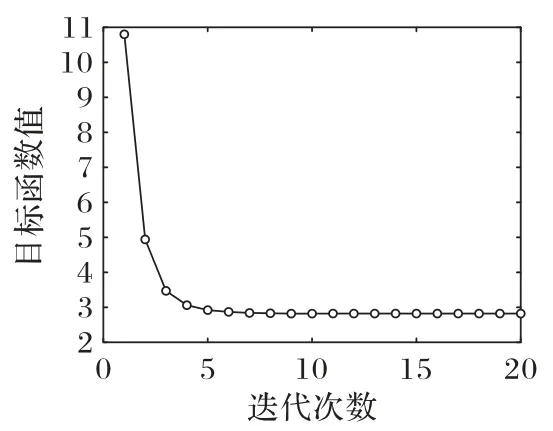
图2 本文方法在NUS-WIDE数据集上的收敛曲线Fig.2 Convergence curve of DMFH on dataset NUS-WIDE

3.4.3 平衡矩阵分析

对比方法DCH 在实验中引入了线性分类器，以使目标哈希码更具辨别性，但该方法的检索性能受到训练后分类器的影响和限制。相比之下，本文方法使用平衡矩阵代替需要训练的分类器，保留哈希向量的平衡条件以最大化哈希码的信息熵。总的来说，与方法DCH 相比，本文方法可以保证哈希码的可区分性，同时避免了分类器性能差带来的影响。

为进一步验证本文提出的平衡矩阵对实验结果的影响，将式（4）代替式（5），按位更新哈希码以优化求解，并重新进行模型训练。去除平衡矩阵项的前后实验结果由表2 给出，可以看到，去掉平衡矩阵后，在MIRFlickr 和NUS-WIDE 数据集上的检索精度都有较大幅度的下降。这说明平衡矩阵能够在一定程度上保持数据的原始语义关系，在本文提出的模型中能有效提高跨模态哈希检索的效率。

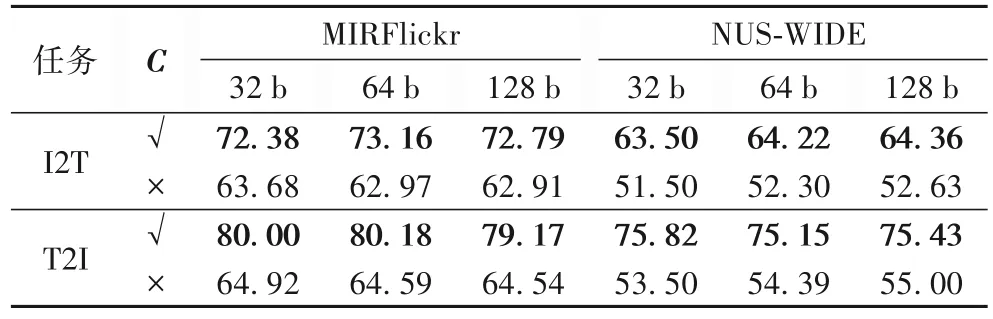
表2 平衡矩阵项C对模型mAP的影响 单位：%Tab.2 Influence of balanced matrix term C on mAP unit：%

3.4.4 相似性矩阵分析

传统方法利用标签一致性来判断语义相似性，即若两个实例共享至少1 个标签，则它们是相似的。因此，在传统的相似度矩阵中，相似的两个实例的相似度关系将被指定为1，否则为0。

为了进一步讨论本文提出的相似性程度矩阵的有效性，表3 展示了传统相似性矩阵S＇与本文提出的精确相似程度矩阵S在本文方法中的性能比较。对比结果表明，精确数值相较于用0 或1 来描述相似程度关系更有助检索性能提升。

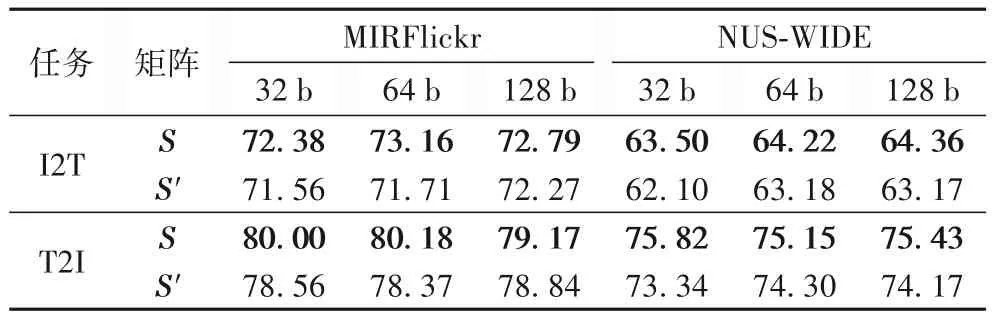
表3 传统相似性矩阵S＇与本文相似性矩阵S的mAP比较 单位：%Tab.3 Comparison of mAP between traditional similarity matrix S＇ and proposed similarity matrix S unit：%

4 结语

为了进行多标签跨模态检索，本文提出了一种新颖的判别性矩阵分解哈希方法。该方法通过协同矩阵分解获得异构数据可共享的隐式子空间，并保持异构数据之间的语义相关性。此外，通过量化隐式子空间中的数据统一表示，直接生成目标二进制码，不仅保持了所学习哈希码的精确相似程度关系，还保持了哈希向量的平衡性。在两个多标签基准数据集上进行了两种任务的对比实验，结果表明本文提出的方法在多标签跨模式检索中是有效的。