判别多维标度特征学习
2023-05-24唐海涛王红军李天瑞
唐海涛,王红军*,李天瑞
(1.西南交通大学 计算机与人工智能学院,成都 611756;2.综合交通大数据应用技术国家工程实验室(西南交通大学),成都 611756)
0 引言
许多实际应用中获取到的数据通常具有很高的维度,如绝大多数的图片数据、文本数据和视频数据。高维数据中的冗余信息不仅会降低后续机器学习任务的性能,还会使后续机器学习任务花费更多算力和内存来处理这些数据,即维度灾难[1]。因此,利用特征学习或降维的方式,通过原始数据得到一个好的低维数据表示成为了许多学者的研究对象。在特征学习的过程中,低维的特征表示在消除原始数据冗余和噪声信息的同时,还要尽可能保留原始数据内在结构。特征学习还有其他许多的应用,包括信息检索[2]以及聚类[3]。
在特征学习中,根据学习过程中是否使用数据的标注信息分为监督、半监督以及无监督的特征学习方法。经典的无监督特征学习方法有主成分分析(Principal Component Analysis,PCA)[4],它的核心思想是寻找一个正交的投影矩阵,使投影后的数据方差最大。半监督方法有半监督降维(Semi-Supervised Dimensionality Reduction,SSDR)[5],它的原理是利用成对约束使低维数据表示更具有判别性。线性判别分析(Linear Discriminant Analysis,LDA)[6]是一种经典的有监督特征学习方法,它的思路是寻找一个正交的投影矩阵,使投影后同类中的样本尽可能接近,不同类别的样本尽可能远离。
另一种划分方式是线性和非线性的特征学习。PCA 和LDA 都属于线性的特征学习,优势在于计算快速,并且当有新样本到来时,可以通过投影矩阵快速计算出新样本的数据表示。与PCA 和LDA 不同的是,基于流形学习的非线性特征学习则是让低维的数据表示尽可能保留原始数据的局部拓扑结构,比如局部线性嵌入(Locally Linear Embedding,LLE)[7],该方法先学习到原始空间中每个样本与邻居间的局部线性关系,然后让数据的低维嵌入尽可能保留在原始空间中学习到的局部线性关系。多维标度法(MultiDimensional Scaling,MDS)[8]则更看重样本间的非相似度,该方法需要先得到样本的非相似度矩阵,然后寻找一个能够尽可能保持原始样本非相似度的低维嵌入。拉普拉斯特征映射(Laplacian Eigenmaps,LE)[9]也是流形学习的代表方法之一,它通过图的拉普拉斯矩阵使得原始空间中相近的样本在低维嵌入后也保持相近。非线性特征学习能够很好地发现数据内部潜在的流形结构,但是面临新样本问题[10]。也有不少算法在投影过程中尽可能保持局部拓扑结构,比如局部保持投影(Locality Preserving Projection,LPP)[11]和近邻 保持嵌 入(Neighborhood Preserving Embedding,NPE)[12],就是分别在LE 和LLE 的基础上增加了投影矩阵。
本文提出了一种基于多维标度法的无监督判别性特征学习方法——判别多维标度模型(Discriminative MultiDimensional Scaling model,DMDS)。该方法一方面使相似度低的样本在低维嵌入中远离,另一方面让相似度高的样本在低维嵌入中尽可能靠近其簇中心,从而使学习到的低维数据表示更具有判别性。该方法使用迭代更新算法求解,并且在12 个公开数据集进行对比实验。结果表明,经过该方法学习到的特征相较于原始空间和传统多维标度法[13]更具判别性。本文的主要工作包括:
1)提出了DMDS 及其对应的目标公式,该目标公式体现了所学习特征在保留拓扑性的同时能增强判别性;DMDS 能在学习低维数据表示的同时发现簇结构,并使同簇的低维数据表示更接近。
2)使用迭代优化方法近似求解目标函数,并根据推理过程设计了相应的算法。
3)在12 个公开数据集上进行实验,评价指标采用聚类平均准确率和平均纯度,实验结果表明DMDS 得到的低维嵌入更具有判别性。
1 相关工作
为了更清晰地了解公式的物理意义,表1 先总结了本文所使用的不同符号的含义。

表1 符号说明Tab.1 Symbol notations
1.1 多维度标度法
给定原始数据矩阵X=[x1,x2,…,xN]∈Rn×N,其中n和N分别表示原始样本的维度和个数;学习到的低维数据表示Y=[y1,y2,…,yN]∈Rl×N,l表示低维数据表示的维度。MDS作为一种保持样本距离的特征学习方法,它的损失函数[14]为:
其中:dij表示原始数据点xi和xj的距离表示对应的低维数据表示yi和yj的距离;S=[sij]∈RN×N是一个非负对称的权重矩阵,sij越大,表示越希望接近dij。文献[9]中给出了两种权重构造方式:
1)热核权重(heat kernel weight):如果xi与xj或xj与xi近邻,则sij=否则sij=0。其中t是一个实数。
2)0-1权重:如果xi与xj或xj与xi近邻,则sij=1;否则sij=0。
式(1)中的MDS 是一种非线性的特征学习方法,得到的直接是低维数据表示Y,如果有新的数据到来,它对应的低维数据表示不能直接获取。所以Webb[13]将投影矩阵融入MDS,提出了带有投影矩阵的MDS(Projective MDS,PMDS),目标公式为:
其中:‖·‖2表示向量的二范数;W∈Rn×l表示投影矩阵,可以看到,Y直接由X投影而来。Webb[13]还通过让同一个类别中低维数据表示距离更近来增加MDS 的判别性。基于此,Biswas 等[15-16]将MDS 应用到低分辨率的人脸识别,并通过同一人的人脸图片的低维数据表示靠近的方式来增加MDS 的判别性。Yang 等[17]进一步考虑了不同人的人脸的低维数据表示距离应该更大,提出了更具有判别性的MDS。
1.2 模糊K均值聚类
高效的聚类算法包括K均值(K-Means,KM)算法[18]、近邻传播聚类(Affinity Propagation,AP)算法[19]以及密度峰值聚类(Density Peak,DP)算法[20]等。随着模糊集理论的提出和完善,模糊聚类[21-22]被提出。模糊聚类能够给出样本与簇的隶属程度,模糊K均值(FuzzyK-Means,FKM)的目标公式是:
其中:C表示簇的个数;U=[uik]∈RN×C是隶属度矩阵,uik表示xi与第k个簇的隶属度;V=[v1,v2,…,vC]是簇中心矩阵,m≥1 表示模糊指数权重。为了提高聚类算法对于高维数据的性能,不少学者将特征学习融入聚类算法,让聚类算法在低维嵌入的过程中发现好的簇结构。比如Hou 等[23]将PCA与K均值结合,让K均值在PCA 学习过程中进行聚类,两者相互影响,从而找到更好的簇结构;Li 等[24]将非负矩阵分解(Non-negative Matrix Factorization,NMF)与K均值结合,在NMF 得到的低维数据表示中进行聚类;Nie 等[25]将PCA 融入FKM,同样在PCA 得到的低维数据表示完成聚类。
2 DMDS
2.1 模型目标函数
在1.1 节详细介绍了MDS,为了增强其特征学习的判别性,不同学者都使用了标签信息进行监督或者半监督学习,但很多时候获取标签信息比较困难。本文采用无监督学习的思想来增加MDS 判别性。DMDS 目标函数如下:
其中:E1表示特征学习过程中尽量保持原有数据的拓扑结构,同时E2期望在学习过程中增加学习到的特征的判别性;α和β分别表示E1和E2的权重。
在式(4)中,如果α取值很小,此时会尽可能让低维数据表示非常靠近;而如果β取值很小,此时将尽可能让低维嵌入保持原始数据的距离。即式(4)的目标公式体现了一方面期望保持样本的原始拓扑信息,另一方面期望同簇样本靠近簇中心,两者相互影响以学习到判别性的数据表示。值得注意的是权重矩阵S,传统的MDS 在特征学习过程中是尽可能保持每个样本与邻居的距离;而在DMDS 中,更看重每个样本距其较远的样本,也就是尽可能使低维数据表示保持每个样本与距其较远的样本的距离,并且通过第二项E2使得低维数据表示中每个样本与其簇中心靠近,从而增加了低维数据表示的判别性。具体而言,权重矩阵构造方式为:
1)改进热核权重:如果xi与xj或xj与xi近邻,则sij=1 -;否则sij=1。其中参数t是一个大于0实数。
2)改进0-1 权重:如果xi与xj或xj与xi近邻,则sij=0;否则sij=1。
2.2 模型推理
式(4)中的目标函数要求解的参数是投影矩阵W、隶属度矩阵U和簇中心矩阵V,由于无法直接得到这三个矩阵的闭式解,故本文采用迭代的方式求解。
1)固定U和V,更新W。此时式(5)是仅关于W的函数:
可以采用迭代优化算法(Iterative Majorization Algorithm,IMA)[8,13]优化式(5)。此时,构造的辅助函数是σ(W,Z),定义为:
其中(·)-1表示矩阵的Moore-Penrose 广义逆。
2)固定W和V,更新U。由于式(4)中E1不含有U,所以只需考虑E2,此时是一个仅关于U的函数:
采用拉格朗日乘子法[26]:
3)固定W和U,更新V。与步骤2)类似,有:
对式(16)求关于vk的梯度并使其为0,即:
2.3 算法描述
根据2.2 节DMDS 的推理过程,算法1 给出了DMDS 算法的整体流程。
算法1 DMDS 算法。
计算矩阵A的时间复杂度为O(n2N+nN2);与矩阵A类似的是,计算矩阵D(Z)的时间复杂度也是O(n2N+nN2);一个n×n的对称矩阵的Moore-Penrose 逆可以通过对它进行奇异值分解来得到,奇异值分解的时间复杂度为O(n3)[27];所以更新一次W的时间复杂度为O(nN2+n2N+n3)。更新一次隶属度矩阵U的时间复杂度为O(NC2l)。更新一次矩阵V的时间复杂度为O(NCl)。则DMDS 算法的时间复杂度为:O(T(nN2+n2N+n3+NC2l)),其中T为最大迭代次数。
3 实验与结果分析
3.1 数据集
为验证DMDS 的性能,在由微软亚洲研究院公开的多媒体数据 集(MicroSoft Research Asia MultiMedia,MSRAMM)[28]和UCI 机器学习数据集上进行实验。MSRA-MM 数据集包括两个子数据集:图像数据集和视频数据集。其中图像数据集包括68 个类别,共计65 433 张图片,每个类别大约有1 000 张。表2 总结了所使用的12 个数据集,前10 个数据集来源于MSRA-MM;最后2 个数据集来源于UCI 机器学习数据集,QSAR_AR 是指QSAR androgen receptor 数据集。

表2 实验数据集Tab.2 Experimental datasets
3.2 评价指标
实验使用了聚类算法的常用两个指标:准确率[23]和纯度[29],并使用Friedman 统计量[30]来进行整体评估。准确率和纯度的取值都是[0,1],并且值越大,代表聚类效果越好。
准确率的计算公式:
其中:N表示样本点的个数;map(·)是一个将簇索引映射到类别标签的函数,一般通过匈牙利算法求得;li和ri分别表示样本点xi的类别标签和簇索引;δ(a,b)是一个函数,当a=b时,函数值为1,否则为0。
纯度定义为:
其中:N表示样本点数;C表示簇数;k表示簇索引;q是类别数,一般而言,q与C相等表示第k个簇中类标签为r的样本数。
Friedman 统计量是一种非参数测试的统计方法,用于评估一组算法在不同数据集上性能的整体差异。Friedman 统计量需要先得到每个算法在同一个数据集上性能的排序,性能最好的算法排序为1,次好的算法排序为2,以此类推可以得到所有算法的排序,如果有相同的性能,则取平均排序值。具体而言,Friedman 统计量定义为:
其中:a表示数据集的个数,b表示算法的个数;Rj=表示第j个算法在第i个数据集上的排序值,可以看出Rj表示的是第j个算法在所有数据集上的平均排序值。服从自由度为b-1 的卡方分布(Chi-square Distribution)。原始Friedman 统计量检验结果相对保守,一般使用式(22)所示的方式进行评估:
FF是自由度为b-1 和(b-1)(a-1)的F 分布,通过查表可计算其p值,基于p值对算法性能进行评估。
3.3 实验设置
为了验证DMDS 的特征学习性能,本文采用了对比实验的方法,即分别对原始的数据表示、PMDS[13]算法得到的低维数据表示和本文提出的DMDS 算法得到的低维数据表示进行多种聚类实验;如果数据表示更具有判别性,那么聚类效果就更好。为了实验的公平性,特征学习算法PMDS 和DMDS 的低维表示的维度都是原始数据维度的1/10;每个聚类算法在不同数据表示上配置的参数一样,簇个数设置为数据集类别数,并且每个聚类算法对同一个数据集都重复运行10 次,然后取10 次结果的均值作为最终结果,以降低实验结果的偶 然性差 异。选择的聚类算法包括KM[18]、AP[19]和DP[20]算法。
对于PMDS 算法,其目标公式中的权重矩阵S使用热核权重,热核权重中使用的近邻关系是K近邻算法,即如果xi是xj的K近邻或者xj是xi的K近邻,则xi与xj具有近邻关系,其中K取样本总数的1/10;热核权重的t=100;距离采用的是样本间的欧氏距离。
对于DMDS 算法,权重矩阵S使用的改进热核权重,改进热核权重中使用的近邻关系也是K近邻算法,其中K取样本总数的9/10(由改进热核权重的定义可知,更希望保留每个样本距离其最远的总样本1/10 的样本的距离);热核权重的t=100;距离采用的是样本间的欧氏距离;模糊指数权重为2。在前10个数据 集中,α和β分 别取1 和1 000;对于CNAE-9 数据集α和β分别取1 和100;QSAR_AR 数据集α和β分别取1 和5 000。
3.4 实验结果
3.4.1 判别性实验结果与分析
表3 和表4 分别给出了12 个数据集在不同数据表示下分别通过KM、AP 和DP 聚类的平均准确率和平均纯度的结果。表3 中,列KM、AP 和DP 是三种聚类算法在原始数据表示上的聚类准确率;PMDS-KM、PMDS-AP 和PMDS-DP 是三种聚类算法在经过PMDS 算法得到的低维数据表示上聚类的准确率;DMDS-KM、DMDS-AP 和DMDS-DP 是三种聚类算法在经过DMDS 算法得到的低维数据表示上聚类的准确率;Avg 表 示KM、AP 和DP 的均值;PMDS-Avg 是PMDS-KM、PMDS-AP 和PMDS-DP 的均值;类似地,DMDS-Avg 是DMDSKM、DMDS-AP 和DMDS-DP 的均值。表4 的表头含义与表3类似,只是表格中数据是平均纯度。
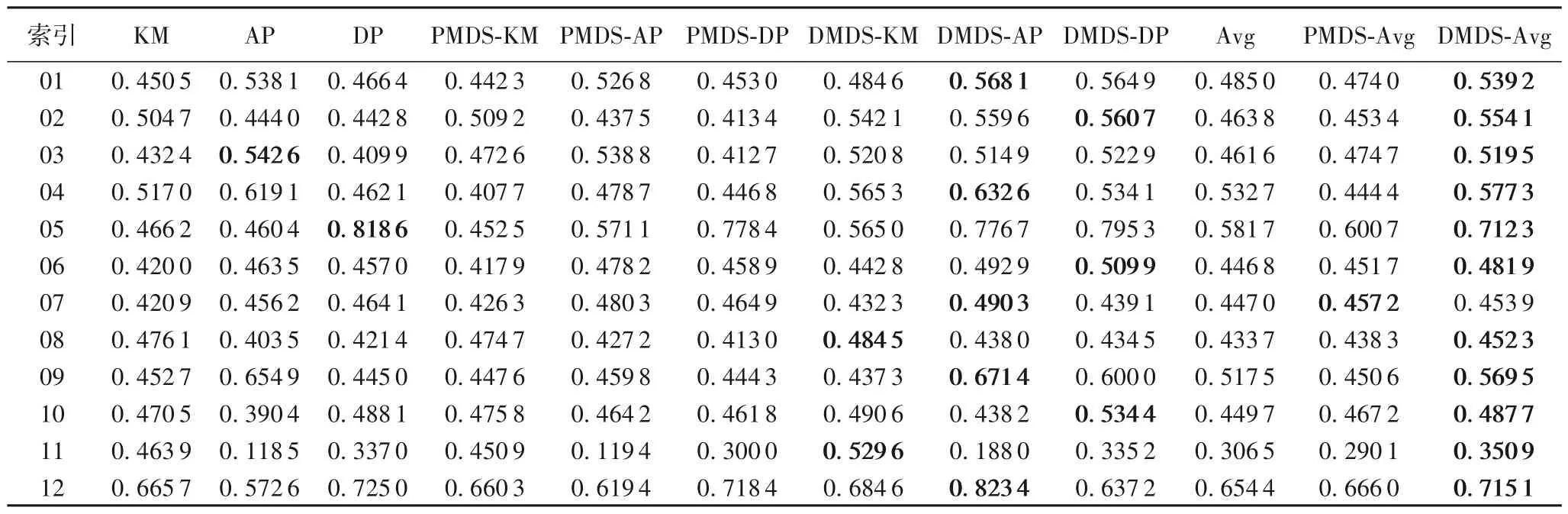
表3 不同数据表示下的平均聚类准确率Tab.3 Average clustering accuracy under different data representations
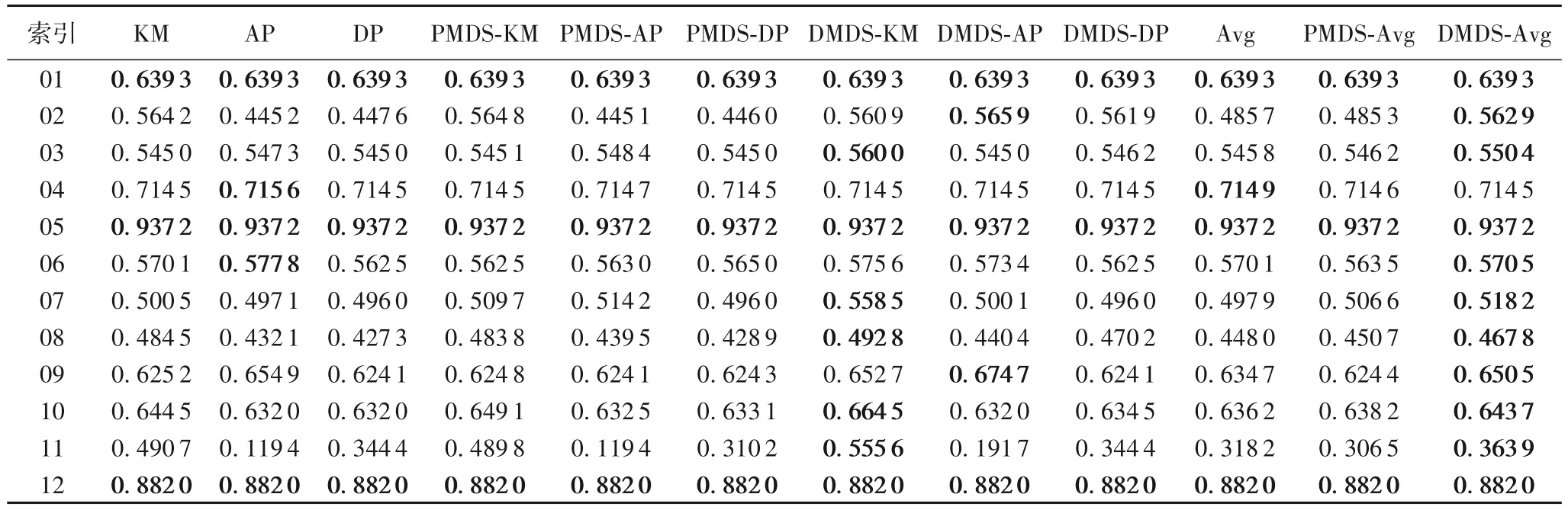
表4 不同数据表示下的平均聚类纯度Tab.4 Average clustering purity under different data representations
从表3 可以看出,在这12 个数据集中,准确率最高的模型有10 个是在经过DMDS 特征学习的数据表示上(表格中的加粗数据),有2 个在原始数据表示上,这说明DMDS 能够提高数据表示的判别性。而且对于同一个聚类算法而言,在DMDS 算法得到的数据表示上表现出来的性能绝大多数时候都优于原始数据表示和PMDS 的数据表示,这也进一步说明了经过DMDS 算法得到的数据表示能够提高后续机器学习任务的性能。另外,从平均准确率来看(即表3 的最后三列),有11 个最高的平均准确率在DMDS 算法的特征表示上,有1 个在PMDS 算法的数据表示上,这也说明了经过DMDS 特征学习算法后得到数据表示更有利于后续机器学习的性能。
然后用Friedman 统计量来评估模型整体的性能。根据表3 最后3 列可以得出每个数据集中不同指标的排序值,比如对于第一个数据集而言,Avg、PMDS-Avg 和DMDS-Avg 的排序值分别为2、3 和1。然后可以得出在12 个数据集上Avg、PMDS-Avg 和DMDS-Avg 的平均排序值分别为2.583 3、2.333 3 和1.083 3。根据平均排序值可计算出Friedman 统计量≈15.500 0,则Iman-Davenport 为FF≈20.058 8。由于数据集有12 个,有3 种不同数据表示,所以FF服从自由度为3 -1=2 和(12 -1)(3 -1)=22 的F 分布。由F(2,22)分布可以计算p值为1.100 × 10-5,所以在高显著性水平下拒绝原假设,即综合评价DMDS 算法优于PMDS 算法,经过DMDS 算法得到的数据表示比PMDS 得到的数据表示和原始数据表示更具有判别性。
表4 列出了在不同数据表示上聚类结果的平均纯度。可以看出,有7 个最高纯度在DMDS 的数据表示上;3 个最高纯度相等;2 个最高纯度在原始数据表示上。总体而言在DMDS 上的聚类性能优于PMDS 和原始空间。另外,从表4的三个平均纯度列来看,也是大部分最高纯度位于DMDS 的数据表示上,这也说明DMDS 的有效性。
同样,用Friedman 统计量来评估模型整体的性能。根据表4 最后3 列可得出Avg、PMDS-Avg 和DMDS-Avg 的平均排序值分别为2.250 0、2.333 3 和1.416 7。可计算出Friedman统计量为≈6.166 7,则Iman-Davenport 为FF≈3.803 7。由F(2,22)分布可以计算p值为0.038 1,所以在较高显著性水平下拒绝原假设,即综合评价DMDS 算法优于PMDS 和原始空间。
从准确率和纯度综合而言,DMDS 得到的数据表示相较于原始数据表示和PMDS 得到的数据表示对于后续的聚类算法都有着更好的性能,能够学习到更具有判别性的特征。
3.4.2 参数敏感度分析
从DMDS 的目标函数式(4)可知,DMDS 通过参数α和β权衡新的数据表示中保持原始空间样本拓扑结构和同簇样本靠近其簇中心的程度,所以本节将讨论不同的α和β之间的比重关系对于特征学习性能的影响结果。
对于每个数据集,在不同的β与α的比值(记为β/α)下分别通过DMDS 学习到新的数据表示,然后通过KM、AP 和DP三种聚类算法进行聚类,根据聚类结果计算出准确率和纯度,以三种聚类算法的平均准确率和平均纯度作为最终结果。β/α选取的比值为{10-1,101,102,103,104}。
图1 给出了12 个数据集的参数敏感度结果。可以看出,随着β/α的比值变化,准确率有明显的变化,纯度变化幅度较 小。对 于voituretuning、border、bicycle、building、banner、wallpaper2、banana 以及bus 这7 个数据集,在β/α为103取得了较好的结果;而对于CNAE-9 数据集,则是在β/α为10-1取得了较好的结果;并且都随着β/α比值的增大性能开始下降。这也说明刚开始β/α比值不是很大时,新的数据表示一方面较好地保留了原始样本的拓扑信息,另一方面同簇的样本更加紧凑,从而能够较好地提高判别性并提高聚类性能。而当β/α比值很大时,此时同簇样本很紧凑以致于原始样本的拓扑信息有了较大的损失,导致性能开始下降。综合而言,在β/α为103附近时,能够达到一个较好的平衡。
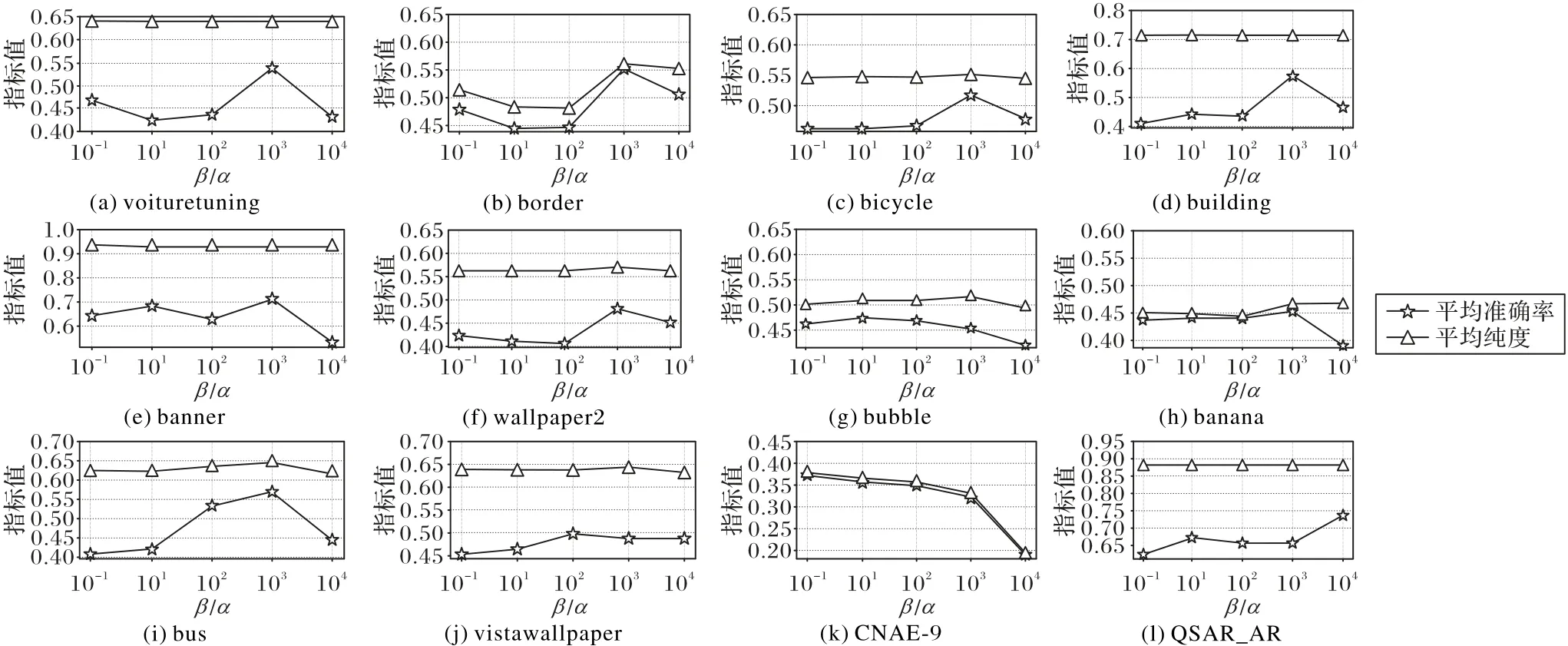
图1 DMDS在12个数据集上在不同β与α的比值下的平均准确率和平均纯度对比Fig.1 Average clustering accuracy and purity comparison of DMDS on 12 datasets with different ratios between β and α
3.4.3 算法运行时间对比
2.3节已经详细分析了DMDS 算法的时间复杂度,为了更直观地表示DMDS 算法与PMDS 算法时间复杂度的差异性,图2 给出了它们迭代500 次所需的时间,可以看出DMDS算法相较于PMDS 算法需要更多的时间。
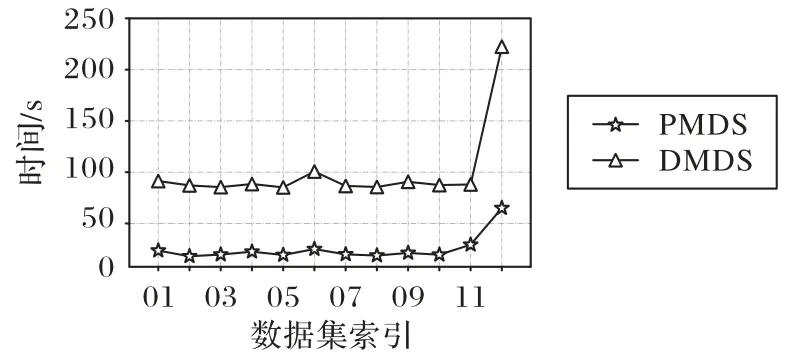
图2 DMDS与PMDS运行时间的对比Fig.2 Running time comparison of DMDS and PMDS
4 结语
本文提出了一种判别多维标度法的特征学习模型DMDS,该模型加强了映射后的数据的判别性,这对后续的数据类别划分尤为重要,从数据内在的特性上提高了数据可划分性。将无监督学习的思想融入多维标度法,通过模糊K均值聚类能够自动发现数据中的簇结构,使得在MDS 学习低维数据表示的过程中,同簇中的样本更加靠近簇中心,原始距离较远的样本远离,从而使学习到的数据表示更具有判别性。本文还使用了一种迭代更新的方法求解目标公式,在公开数据集上进行实验。实验结果表明,DMDS 能够学习到更具有判别性的特征,从而提高后续机器学习任务的性能。
从3.4.2 节可以看出DMDS 算法受到超参数α和β的影响比较大,所以在未来的工作中,将致力于减少算法中的超参数,或者让超参数能够自动适应数据,从而进一步提高算法的性能。此外,也将研究如何使用部分监督信息(如样本成对约束信息)来进一步提高DMDS 学习的特征的判别性。
