迭代修正鲁棒极限学习机

吕新伟，鲁淑霞*

（1.河北省机器学习与计算智能重点实验室（河北大学），河北 保定 071002；2.河北大学 数学与信息科学学院，河北 保定 071002）

0 引言

极限学习机（Extreme Learning Machine，ELM）自提出以来，已经成功应用于各种实际问题［1-5］，成为广泛使用的机器学习工具之一。ELM 主要依赖于给定的训练数据标签，如基于L2范数损失函数的ELM［6］假设训练标签的误差是一个正态分布；然而，实际问题中的训练样本不能保证误差具有正态分布。此外，ELM 往往过分强调训练过程中残差较大的异常点，导致ELM 对异常点的敏感性和鲁棒性较差。因此，构造能够抑制异常点影响的鲁棒极限学习机（Robust ELM，RELM）模型，在机器学习中是必要和有意义的。

ELM 的许多变体都致力于提高ELM 对异常点的鲁棒性。引入正则化的极限学习机［7-9］通过在最小化目标函数中添加正则化项以减小结构风险，如加权极限学习机（Weighted ELM，WELM）［10］和鲁棒极限学习机（RELM）［11］为训练样本分配适当的权值，但它们的性能在很大程度上依赖于权重估计的初始值。Chen 等［12］基于正则化项和损失函数的多种组合设计了迭代重加权极限学习机（Iteratively Re-Weighted ELM，IRWELM），并通过迭代加权算法实现。最近的一些研究则通过替换损失函数来增强极限学习机的鲁棒性，例如使用Huber 损失函数［13］、L1范数损失函数［14］以及各损失函数的变体［15-16］等实现鲁棒极限学习机，以减少异常点的影响；但它们仍然不够稳健，因为这些损失函数受到残差较大的异常点的影响。具有相关熵损失函数［17］和重标极差损失函数［18］的极限学习机改进版本倾向于构造有界和非凸损失函数，以提高对异常点的鲁棒性。尽管这些损失函数具有良好的学习性能，但是求解该优化问题的方法过于复杂。有界的损失函数可以抑制残差较大异常点的影响，迭代重加权正则化极限学习机（Iterative Reweighted Regularized ELM，IRRELM）［19］通过有界的L2范数损失函数抑制较大异常点的负面影响；但过多的异常点反过来会影响损失函数对异常点的判定，影响回归结果。因此本文在有界L2范数损失函数的基础上使用迭代修正方法，提出了一种用于回归估计的鲁棒极限学习机，以抑制异常点的负面影响，采用迭代加权算法求解鲁棒极限学习机。在每次迭代中，为本轮认为是异常点的标签重新赋值，并在每次迭代的过程中逐渐去除异常点的影响，增强极限学习机的鲁棒性。

本文的主要工作包括：为减小极端异常点的影响，采用了有界损失函数，并在有界损失函数的基础上提出了迭代修正鲁棒极限学习机（Iteratively Modified RELM，IMRELM），让这些残差较大的异常点在迭代的过程中找到正确的标签。实验结果表明，当数据中的异常点数过多且残差较大时，本文IMRELM 的结果优于对比的几种鲁棒极限学习机算法。

1 相关工作

1.1 极限学习机

假设有N个任意样本，其中：xi∈Rd为输入变量；yi∈R 是回归估计中相应的目标。ELM 是一个单隐层神经网络，具有L个神经元的ELM 的输出函数可以表示为：

其 中：β=[β1，β2，…，βL]T为 ELM 输出权 重；h(x)=[h1(x)，h2(x)，…，hL(x)]为隐含层矩阵；f(x)为回归估计中相应的目标预测值。

ELM 求解以下优化问题来推导输出权重β：

s.t.h(xi)β=yi-ei；i=1，2，…，N

其中：ei是训练误差；C是平衡模型复杂度的正则化参数。基于最优性条件，得到式（2）的最优解β：

其 中：数据的 真实标 签y=[y1，y2，…，yN]T；H=[h(x1)，h(x2)，…，h(xN)}T是隐藏层输出矩阵；I为适当大小的单位矩阵。

1.2 迭代重加权正则化极限学习机

为了减小L2范数损失函数对于残差较大异常点的敏感性，IRRELM 使用了非凸L2范数损失函数。

其中：z是一个变量；θ是一个常数，θ是对大异常点的惩罚。g(z)的上界意味着损失在一定值后不会增加惩罚，并且它抑制了异常点的影响。

IRRELM 的优化模型为：

s.t.h(xi)β=yi-ei；i=1，2，…，N

在迭代重加权中，每个样本的权重通过残差由下式给出：

IRRELM 的第k次迭代解为：

在IRRELM 中，βk为第k次迭代中求得的隐层输出权重；wk=diag(w1，w2，…，wN)为第k次迭代样本权重。

算法1 IRRELM 算法。

2 迭代修正鲁棒极限学习机

对于鲁棒极限学习机，通常都是减小异常点的影响。但是基于L2范数损失函数的ELM 对异常点非常敏感，当数据中存在异常点时，异常点L2范数损失会很大。因此，选择损失较小的数据进行训练模型是有效的。为了避免过多异常点污染模型以及数据和资源的浪费，同时解决模型泛化能力不强的问题，在每次迭代中，对于那些残差较大的数据进行修正。

为了处理异常点，本文提出了一种迭代修正鲁棒极限学习机算法。

在IRRELM 中，优化模型又可以写成：

令tik=1 -wik，提出以下损失函数：

优化模型为：

优化模型关于β求导并令其等于零，得到迭代修正鲁棒极限学习机的解为：

其中：H=[h(x1)，h(x2)，…，h(xN)]T；wk=diag(w1，w2，…，wN)，tk=diag(t1，t2，…，tN)；C1、C2为正则化参数；I为适当大小的单位矩阵。

算法2 IMRELM 算法。

3 实验与结果分析

为了研究IMRELM 的有效性，在人工数据集和真实数据集上进行了数值实验。通过10 次交叉验证和网格搜索方法选择实验参数。所有上述算法选择的参数的范围如下：参数kmax：{10i，i=2，3，4}，停止阈值p：{10i，i=-5，-4，…，1，2}，正则化参数C1、C2：{10i，i=-5，-4，…，4，5}。所有的实验都在3.40 GHz 的机器上使用Pycharm 2019 进行。

比较算法是极限学习机（ELM）和一些鲁棒极限学习机，包括加权极限学习机（WELM）、迭代重加权极限学习机（IRWELM）和迭代重加权正则化极限学习机（IRRELM）。在实验中，使用sigmoid 激活函数g(x)=1/(1+exp(-x))。迭代加权的算法中的迭代次数为200，采用均方误差（Mean-Square Error，MSE）作为估计标准：

其中：N是测试集的数量；yi、f(xi)分别是真实值和相应的预测值。通常，均方误差越小，方法的性能越好。

3.1 IMRELM在人工数据集上的实验

在不同异常点水平的人工数据集上进行实验，结果给出了IMRELM 算法和其他算法的实验结果，并通过统计测试比较了这些算法的性能。人工数据集来源于回归问题中广泛使用的函数，定义如下：

实验在具有不同异常点水平的人工数据集上进行，并通过统计测试比较这些算法的性能。在实验中，噪声是［-10，10］上的均匀分布。按照数据的大小随机生成不同占比的噪声并添加到训练集上。为了揭示IMRELM 算法的鲁棒性，在不同水平异常点（包括0%、10%、20%、…、80%）数据集上分别进行对比实验。在具有不同异常点水平的噪声环境情况下，对比了几个改进的极限学习机的鲁棒性。对于每个异常点水平，在50 次独立运行中进行实验，以避免不公平的比较，并获得了表1 中的均方误差和标准差（Std）。

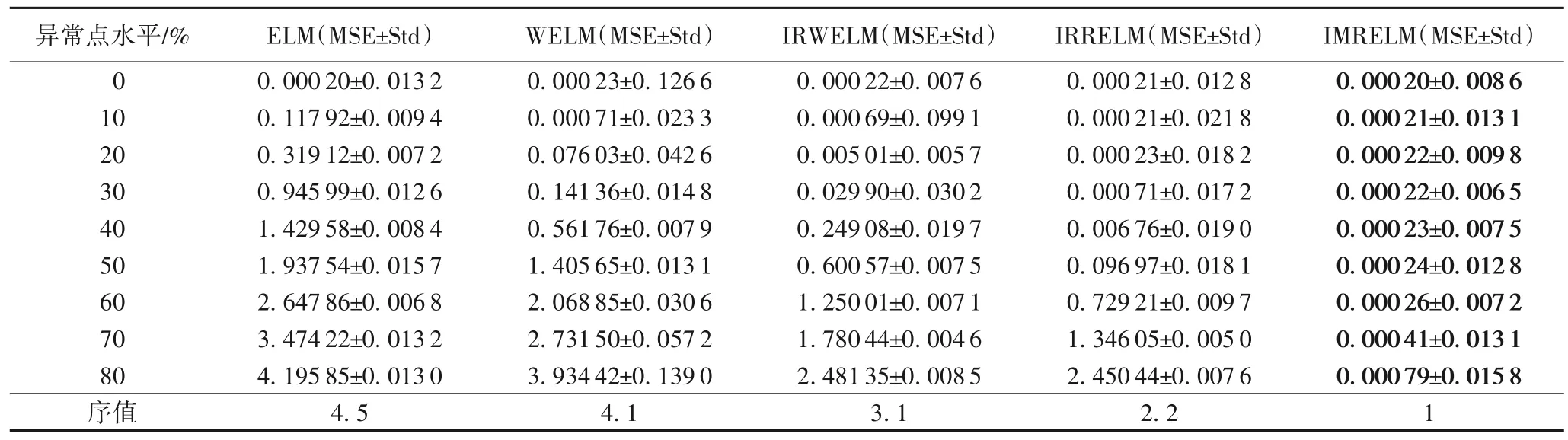
表1 具有不同异常点水平的人工数据集上的实验结果Tab.1 Experimental results on synthetic datasets with different outlier levels

从表1 可以看出，在没有异常点的情况下，经典ELM 表现出了很好的性能，具有最小的均方误差值。IMRELM 的表现优于WELM、IRWELM 和IRRELM。在不同异常点水平的情况下，ELM 在所有水平上的表现都较差，反映了它对异常点的敏感性。

对于人工数据集，得到=26.244 和FF=21.520 2。在Friedman 测试中，如果α=0.05，得到Fα=2.157＜21.520 2。因此，拒绝“两个算法性能相同”这一假设。继续进行Nemenyi 检 验，α=0.1，qα=2.459，CD=1.832 8。如 表1 所示，IMRELM 和其他4 种鲁棒性方法之间的排名差异为3，3，3，2 和1，因此，得出的结论是：IMRELM 的性能明显不同于ELM、WELM、IRWELM，并且IMRELM 的性能最好。

为了更清楚地显示这些算法的性能，图1 显示了在均匀分布噪声下，5 种算法在不同异常点水平下的回归曲线：当数据中没有异常点时，5 种算法与原始曲线（SIN）拟合较好；当数据中异常点占比到30%时，WELM 开始偏离原始曲线；当数据中异常点占比到50%时，IRWELM 开始偏离原始曲线；当数据中异常点占比到60%时，IRRELM 开始偏离原始曲线。可以看出随着数据中异常点水平的增加，ELM、WELM、IRWELM 和IRRELM 曲线部分偏离原始曲线，朝向异常点，而IMRELM 的曲线始终最接近原始曲线。

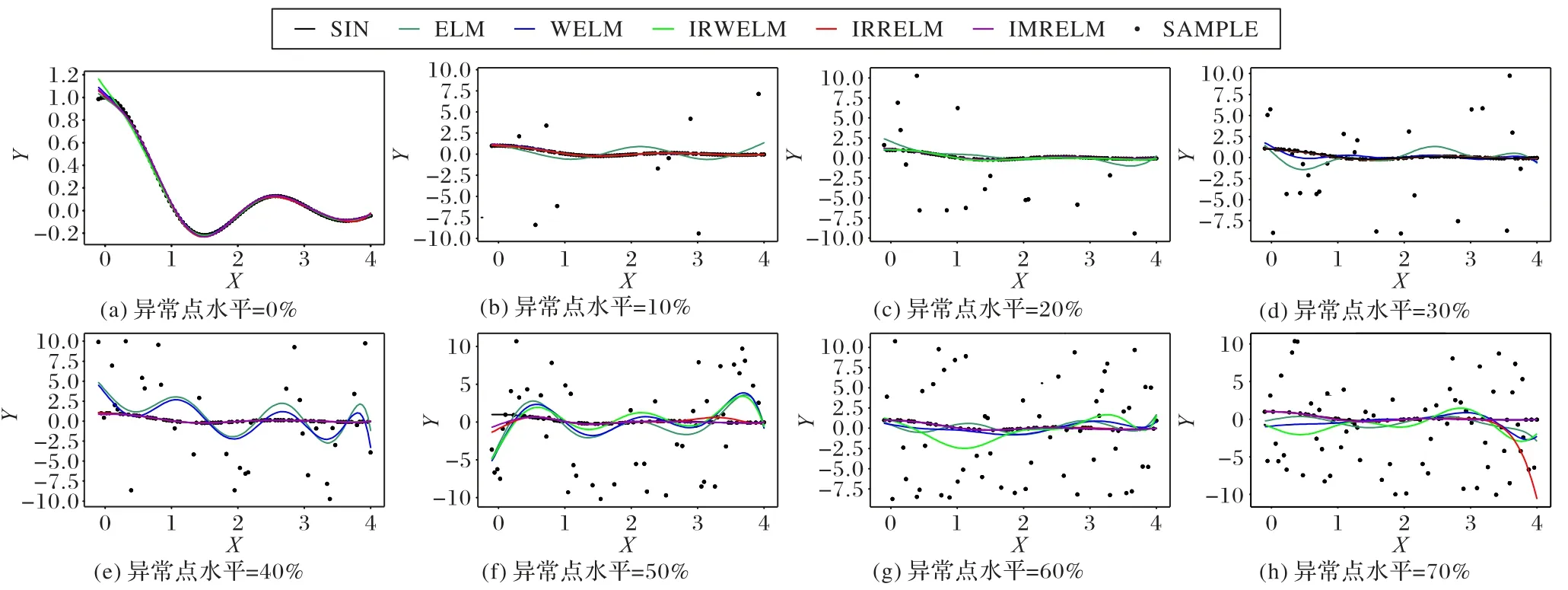
图1 五种算法在不同异常点水平下的回归曲线Fig.1 Regression curves of five algorithms under different outlier levels

3.2 IMRELM在真实数据集上的实验

在12 个真实数据集上进行了进一步的实验，以验证IMRELM 在处理噪声和异常点的有效性。在数据准备过程中，根据训练样本和测试样本的数量，将每个数据集随机分为两部分（训练集和测试集）（见表2）。在训练集和测试集中，所有特征均归一化为零平均值，标准残差为1。真实数据集都来自UCI［20］。

表2 真实数据集Tab.2 Real datasets

从表3 可以看出，在没有异常点的情况下，ELM 和极限学习机的其他4 种ELM 变体实现了相似的预测精度。当在具有异常点的数据集上进行训练时，如均方误差所反映的，ELM 的性能最差，它的性能随着异常点水平的增加显著下降，这表明ELM 对异常点不具有鲁棒性；其他算法的预测精度要高得多，且IMRELM 在大多数情况下都优于其他算法。

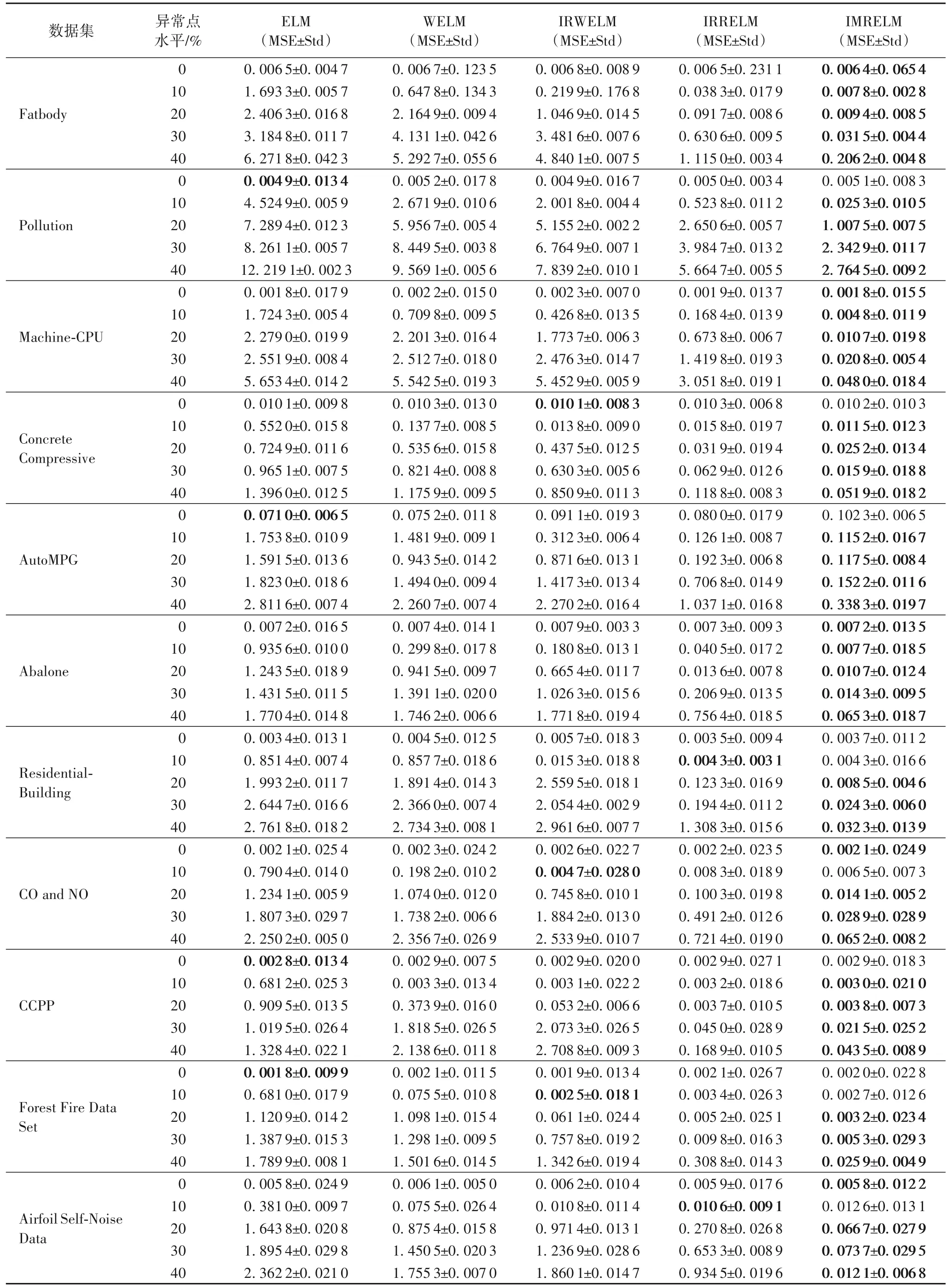
表3 具有不同异常点水平的真实数据集上的实验结果Tab.3 Experimental results on real datasets with different outlier levels

接下来通过Friedman 测试来讨论这5 种算法在12 个真实数据集上的性能。表4 展示了几种鲁棒算法在实际数据集上的平均排名；表5 中展示了Friedman 测试的相关数据，其中Δ（IMRELM-ELM）表示IMRELM 和ELM 的序值差。在真实数据集上FF均大于Fα，因此，拒绝在这12 个真实数据集上的“两个算法性能相同”这一假设。因为Δ（IMRELMELM）、Δ（IMRELM-WELM）的值均大于CD值1.832 8，所以IMRELM 与ELM、WELM 和IRWELM 的性能有明显的差异。Δ（IMRELM-IRRELM）、Δ（IMRELM-IRWELM）的值均 在1左右。

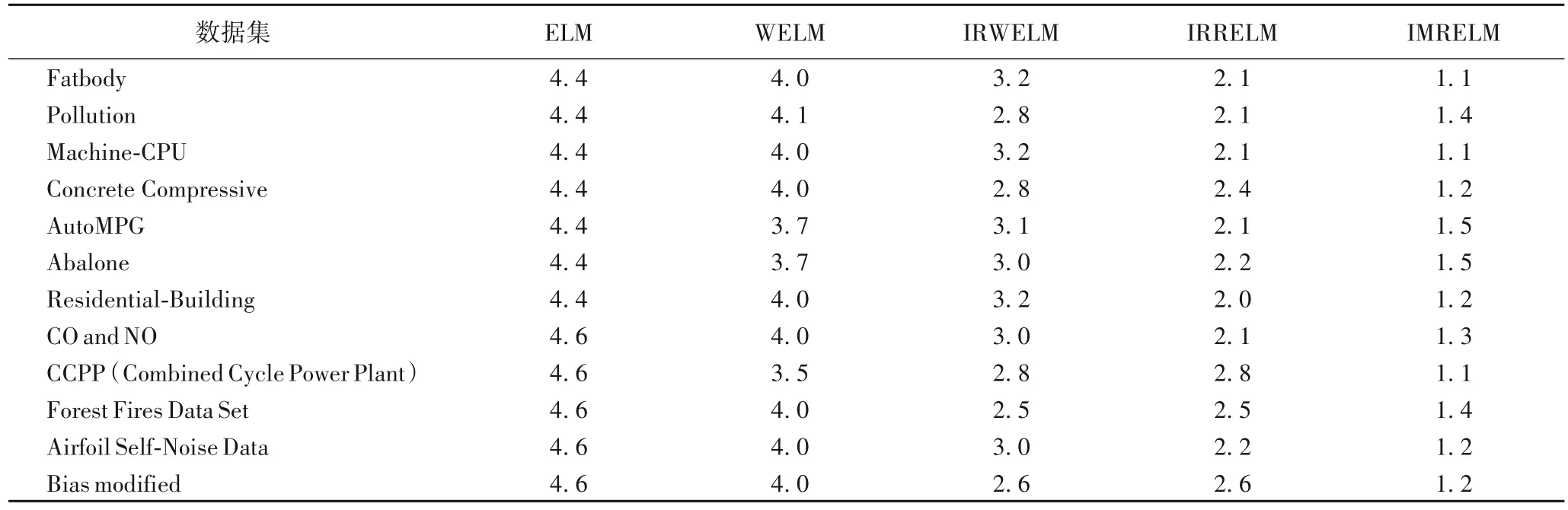
表4 五种算法在12个真实数据集上的平均序值Tab.4 Average order values of five algorithms on 12 real datasets

综上，可以得到IMRELM 在含有异常点的数据集上的预测精度最好。

4 结语

在实际应用的真实数据集中往往含有离群值，这会导致ELM 的泛化性能较差。为了抑制异常点的负面影响，提高ELM 的鲁棒性，提出了迭代修正鲁棒极限学习机（IMRELM）算法，使用迭代重加权的方法进行优化。IMRELM 在每次迭代中将离群值的权值设为0，并重新进行标签赋值。因此，最小化目标函数时不涉及离群值，可以增强ELM 的鲁棒性。在1 个人工数据集和12 个不同离群值水平的真实数据集上的对比实验结果表明，IMRELM 具有良好的预测精度和鲁棒性。但目前IMRELM 中只考虑了原始ELM 中的L2范数损失函数，在未来的工作中也可以拓展到其他ELM 变体中的损失函数，如Huber 损失极限学习机、L1范数损失极限学习机和铰链损失极限学习机，以获得稳健的极限学习机模型。