属性聚类下三支概念的对比
2023-05-24张晓燕王佳一
张晓燕,王佳一
(西南大学 人工智能学院,重庆 400715)
0 引言
形式概念分析[1]作为一种数据分析和知识处理的数学工具,它的主要思想是以形式背景为研究对象,以形式概念与概念格为核心概念,通过概念之间的偏序关系刻画对象和属性的内在关系[2]。因此,该理论是一种非常有效的可视化数据处理方法。然而,传统的形式概念分析理论只研究了数据“共同(被)具有”关系的问题,而忽略了“共同不(被)具有”关系的问题[3-4],导致现实应用中该理论具有一定的局限性[5]。
2014 年,Qi 等[6]提出了新的形式概念分析理论,即三支概念分析。三支概念分析是将三支决策理论与概念格相融合,提出了对象诱导的三支概念格与属性诱导的三支概念格。这两种三支概念格均同时研究了“共同(被)具有”和“共同不(被)具有”的关系。它们获得的概念更加精确,构建的三支概念格相较于以往经典概念格,在实际应用过程中概念识别也会更加精确。
在三支概念正式提出后,许多学者对此进行了扩展和深入研究。Qian 等[7]利用形式背景的叠置与并置,提出了三支概念格的构造方法,并仿照对象诱导概念格与属性诱导概念格给出了对象诱导的三支面向对象概念格和属性诱导的三支面向属性概念格的定义,分析了四种概念之间的异同。苏新等[8]比较研究了基于对象和基于属性的三支概念格合并方法。Wei 等[9]立足于三支概念格,在三支协调的意义下研究了决策背景的规则获取问题,并与强协调决策背景所获得的一般决策规则进行了详细的比较研究。
除了对三支概念本身的研究外,学科交叉融合也极大扩展了三支概念的前景。Li 等[10]将多粒度与三支概念结合,研究了基于多粒度的三支认知概念学习模型。龙柄翰等[11]建立了模糊三支概念分析,将模糊集理论与三支概念分析相融合,重点考虑模糊背景中“共同具有的程度”与“共同不具有的程度”两方面不确定的共性信息,为三支概念在模糊领域的实际应用奠定了较好的基础。
在多粒度研究方面,对象粒化、属性粒化以及关系粒化等概念[12-13]的提出将多粒度与概念认知联系起来。这些研究缓解了庞大的概念个数,在约束宽松的情况下减小了时间空间复杂度,并且为获取数据的多层次概念知识表示与处理方法提供了新的方法[14]。多粒度方面的研究主要包括对象(属性)的粗化与细化研究。属性粒化也称为属性的吸收和分解,在粒化过程中概念也会随之转化,从而可以获得在不同粒度空间的形式概念。另外,Belohlavek 等[15]通过粒度树与剪枝研究了给予属性粒化的形式概念分析方法,从而生成不同粒度层次的形式背景。然而,剪枝的构造过程中要求不同粒度层次的属性在某种意义上存在偏序关系。这一条件较为苛刻,甚至难以实现。基于此种局限,Liu 等[16]推广了该方法,提出了属性聚类的概念,即设定一个等价类条件,再以此为基础进行属性吸收,从而构建多粒度层次。
然而,在多粒度层次方面,对三支概念的研究尚且不足。同时,目前的研究无法通过粒度转化直接得到多粒度概念格和多粒度三支概念格,这对于多个粒度层次下的分析十分不利,且需要大量冗余的计算[17]。针对该情况,本文提出以属性聚类为基础的三支概念构建,并重点研究不同概念格下的三支概念转化,进一步丰富三支形式概念分析理论。
1 基础知识
1.1 概念格
设有形式背景K=(G,M,I),其中:G为对象集,M为属性集,I为G和M之间的二元关系。在经典形式背景中,I的取值只有0 或1 两种可能。对于x∈G,m∈M,当I(x,m)=1时,表示对象x和属性m存在关系I;当I(x,m)=0 时,表示对象x和属性m不存在关系I。
为研究对象子集和属性子集之间的关系,现给出两个导出算子,分别作用于属性子集和对象子集,对于X⊆G,A⊆M,有:
特别地,当对象子集或属性子集中仅有一个元素时,记{x}*为x*,记{m}*为m*。
对于形式背景K=(G,M,I),若对于X⊆G,A⊆M,有X*=A且A*=X,则(X,A)称为一个形式概念,其中概念的外延为X,概念的内涵为A。形式背景K=(G,M,I)下的所有形式概念的集合为L(K),L(K)即为概念格[18]。
概念的上下近似算子定义如下:
由上可知,上下近似算子将本身较为严格的概念格约束放宽,使概念格更具实际意义。根据上下近似算子,可以定义新的算子形成面向对象和面向属性的概念格。
对于形式背景K=(G,M,I),若对于X⊆G,A⊆M,有Xu=A且Ad=X,则(X,A)称为面向属性的概念。在形式背景下,所有面向属性的概念称为面向属性概念格,即Lp(K)。进一步,若有Xd=A且Au=X,则(X,A)可被称为面向对象的概念。所有面向对象的概念称为面向对象概念格,即LO(K)。
1.2 三支概念格
如果说概念格研究的是共同具有的关系,那么三支概念格就是同时研究共同具有和共同不具有两个关系。在应用中,单方面的研究往往具有片面性,从正反两方面研究能使研究结果更精准,提高概念分析的正确率。
为了研究共同不具有的关系,下面给出负算子[19]的定义。对于子集X⊆G,A⊆M,有:
显然,通过负算子可以表示并研究形式背景的“共同不具有”这一关系。但如果需要同时研究具有和不具有的关系,还需要定义一对算子。需要特别说明的是,单个对象子集在运算后会得到两个属性子集,即共同具有的属性和共同不具有的属性。同理,单个属性子集在运算后也会得到两个对象子集。因此,由于出发点的不同,可以得到下面两种三支概念。
对 于X⊆G和A,B⊆M:XO=(X*,),(A,B)O=A*∩。当XO=(A,B)且(A,B)O=X,则称(X,(A,B))为对象诱导的三支概念,简称OE 概念,其中X为OE 概念的外延,(A,B)为OE 概念的内涵。
对 于X,Y⊆G和A⊆M:AA=(X,Y)A=X*∩。当AA=(X,Y)且(X,Y)A=A时,则称((X,Y),A)为属性诱导的三支概念,简称AE 概念,其中(X,Y)为AE 概念的外延,A为AE 概念的内涵。
类似地,对于上下近似算子,也有相似的负算子定义:
于是,根据负算子可以有面向对象三支概念和面向属性的三支概念。对于X⊆G和A,B⊆M,定义:XO'=(Xd,),(A,B)O'=Au∩当XO'=(A,B) 且(A,B)O'=X,则 称(X,(A,B))为面向对象的三支概念,简称OEO 概念,其中X为OEO 概念的外延,(A,B)为OEO 概念的内涵。在形式背景K=(G,M,I)中,所有对象诱导的面向对象三支概念的集合被称为对象诱导的面向对象三支概念格,记为OEOL(K)。
对 于X,Y⊆G和A⊆M,定 义:AA'=(Ad,),(X,Y)A'=Xu∩。当AA'=(X,Y)且(X,Y)A'=A时,称((X,Y),A)为面向属性的三支概念,简称AEP 概念,其中(X,Y)为AEP 概念的外延,A为AEP 概念的内涵。在形式背景K=(G,M,I)中,所有属性诱导的面向属性三支概念的集合被称为属性诱导的面向属性三支概念格,记为AEPL(K)。
无论是OE 概念、AE 概念、OEO 概念还是AEP 概念,均在定义中利用了负算子,即同时研究了共同具有和共同不具有的问题,它们的区别在于概念形成的过程和约束。
对于形式背景K=(G,M,I),给定任意x∈G和m∈M,则有下列结论成立:
1.3 属性聚类
在实际应用中,形式背景往往包括大量的属性和对象,但在某个具体的研究中,往往不需要研究全部的属性,因此属性约简或属性吸收就显得尤为重要。属性聚类作为一种较为通用的属性吸收方法,是基于粒度树和剪枝的属性粒化的推广。属性聚类的获取过程更简便,不要求聚类之前与之后的属性存在实际意义上的偏序关系,因此也具有更好的适用性。
属性聚类的特征是基于某种特定需求或者先验关系的。通过等价关系的作用,部分属性被聚合起来,形成新的属性(集)。需要特别说明的是,虽然新的属性集中元素均是以聚类之前的属性为元素的集合,但在新的形式背景下,每个集合被看作一个整体,被称为新的属性。
对于形式背景K=(G,M,I),R为先验关系或特定关系确立的等价关系,[m]R为包含属性m的属性等价类,属性聚类后形成的新形式背景(G,MR,IR)[12]如下:
相较于旧的形式背景,新的形式背景的对象集相同,但属性集发生了变化,新的属性和旧的属性存在包含与被包含关系,属性聚类是一个由细粒度到粗粒度的过程。因此,在属性聚类下,可以在不同层次、不同粒度下进行研究。
2 属性聚类前后三支概念的变化
2.1 属性聚类的推广
在第1 章属性聚类过程中定义对应关系时,采用了乐观定义方法,即在构成新属性的属性集中,只要有一个属性可以与对象x构成关系I,那么新的属性就与对象x构成关系IR。这在应用中会存在一定的局限性。如在日常生活中,常常会遇到以下语境——“以下五条条件中符合三条的获得评比资格”或者“符合以下所有条件的获得评比资格”。这便是不同的属性聚类方式。
为解决此类问题,下面定义悲观属性聚类和一般属性聚类。
定义1对于形式背景K=(G,M,I),R为先验关系或特定关系确立的等价关系,[m]R为包含属性m的属性等价类,悲观属性聚类后形成的新形式背景(G,)如下:
显然,乐观属性聚类与悲观属性聚类均为一般属性聚类的特殊情况:当N(m)=1 时,为乐观属性聚类;当N(m)=|[m]R|时,为悲观属性聚类。因此,在研究属性聚类性质的时候,只需要研究一般属性聚类的性质然后通过改变N(m)取值研究乐观属性聚类与悲观属性聚类的情况。
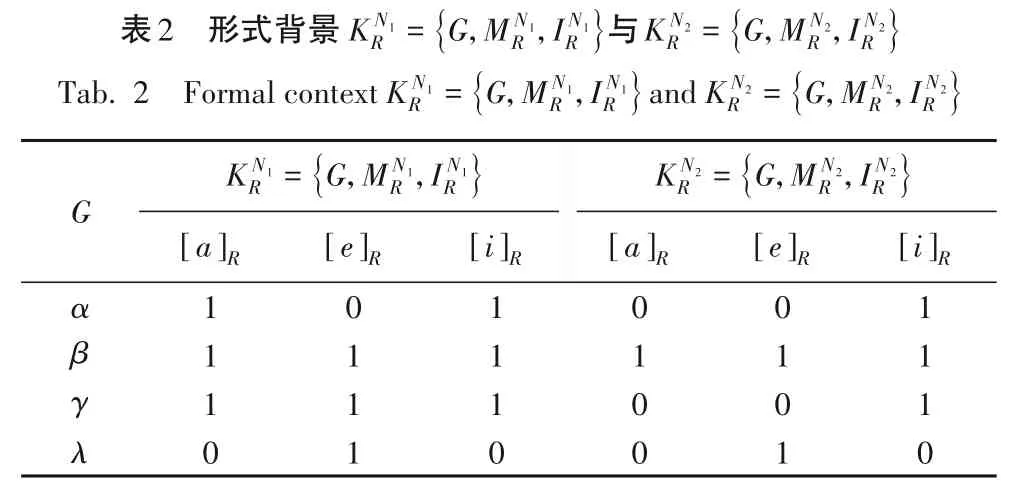
例1 表1 为某形式背景K=(G,M,I),现给出一组R等价类的选取方式以及两组不同的N(m)取值,构建两个形式背景和如表2。
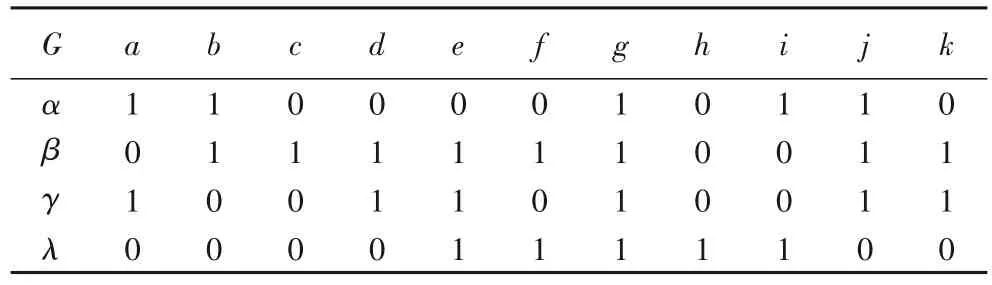
表1 形式背景 K=(G,M,I)Tab.1 Formal context K=(G,M,I)
现给出一组等价类R的构造方法,即归属于同一等价类的属性,在此定 义下均 为等价:[a]R={a,b,c,d},[e]R={e,f,g,h},[i]R={i,j,k}。
给出两组([m]R,N(m))的取值,用来比较研究N(m)取值的大小对属性聚类结果的影响:
根据此给出如表2 所示的两个形式背景。
2.2 属性聚类下三支概念格的表示
为了研究在属性聚类后三支概念的影响,建立在同一对象集下,属性聚类前后三支概念的联系,故在本文中利用等价类的方式表示属性集。对于属性集M={m1,m2,…,mn},在聚类后以等价类的方式表示为:
证明 这里只证明1)、3)、5)、7)、9),其余证明过程类似。
由定义3 可知,R粒度一般属性聚类形式概念也是概念,符合基本概念的相关性质。
定 义4当存在一组XOR=(A,B) 且(A,B)OR=X,则(X,(A,B))为R粒度一般属性聚类对象诱导的三支概念,简称为OER 概念,其中X为OER 概念的外延,(A,B)为OER 概念的内涵。记所有OER 概念为OER 概念格,即OERL()。
定 义5当存在一组AAR=(X,Y) 且(X,Y)AR=A时,((X,Y),A)为R粒度一般属性聚类下属性诱导的三支概念,简称为AER 概念,其中(X,Y)为AER 概念的外延,A为AER概念的内涵。记所有AER 概念为AER 概念格,即AERL()。
于是可得OER 概念与AER 概念均为三支概念,满足三支概念相关性质。
2.3 属性聚类前后三支概念的比较
在多粒度形式概念的构造中,往往采用分别构建的方法,这就造成了大量冗余计算以及资源的浪费。事实上,在构建多粒度过程中,不同粒度的形式背景存在关联。这种关联可以作为推导路径,辅助构建多粒度形式概念。
在R水平一般属性聚类之后,新的属性由原属性集组成,新的对应关系可由原对应关系表示。任何原属性集中的属性,都能在新属性集中找到对应小属性集合包含,且该属性集合的存在是唯一的。
三支概念的一种较为简单的获取方式是利用Ⅰ型混合背景与Ⅱ型混合背景,这种方法比直接利用定义求解更加迅速直观。在经过R水平一般属性聚类后,经原则计算,新形成的属性要么与某对象存在关系,要么不存在关系。以OE 概念与OER 概念(X,(A,B))为例,对于确定的对象集X,在其聚类前的属性集合对(A,B),与其聚类后的属性集合对(如果存在),记为(AR,BR)。任取AR中的元素[m]R,必有超过N(m)个元素与对象集X中任意元素存在关系I。且根据等价类的提取原则,AR中各个[m]R交集为空。即有:
同理,任取BR中的元素[m]R,必有超过个元素与对象集X中任意元素不存在关系I。且根据等价类的提取原则,BR中各个[m]R交集为空。即有:
对此可以看出,经过属性聚类的三支概念事实上是对本身严格的约束条件予以放松处理。但是,该放松处理并不是无限放松,而是有一定限度的。接下来,给出最低约束指数的定义来度量这种放松限度。
根据其性质,也可记为:
显然,eOER的大小与等价类R以及N(m)有关。因此,在进行属性约简时,如果等价类R已确定,可以通过调整N(m)的设定提高eOER;如果N(m)已经确定,可以通过调整等价类R提高eOER。
于是,可知以下性质成立:
性质2 对于AE 概念和AER 概念((X,Y),A),以及指定的对象集合对(X,Y),记由I和确定的属性集分别为A与AR。对于任取[m]R∈AR,必有[m]R∈X*R且[m]R∈,则对于[m]R必须同时满足:
显然,类似于最低OER 约束指数,eAER的大小依然与等价类R以及N(m)有关。因此,在进行属性约简时候,如果等价类R已确定,可以通过调整N(m)的设定来提高eAER;如果N(m)已经确定,可以通过调整等价类R来提高eAER。
例3(续例2)针对例2 给出的四个概念格,计算相应的eOER及eAER。
3 结语
本文是对多粒度属性聚类和三支概念的融合。首先,将属性聚类推广为一般属性聚类、乐观属性聚类与悲观属性聚类三种情况;然后通过对比属性聚类前后三支概念的构成,定义了度量属性聚类对三支概念的放松影响的两个指数;接着研究发现属性聚类过程中等价类的选取以及约束条件的选择是影响指数大小的两个因素,进一步完善了三支概念分析理论。
