多学习行为协同的知识追踪模型

张 凯，覃正楚，刘 月，秦心怡

（长江大学 计算机科学学院，湖北 荆州 434023）

0 引言

智能导学系统（Intelligent Tutoring System，ITS）和大规模在线开放课程（Massive Open Online Course，MOOC）等智慧教育平台逐渐被大众接受，然而智慧教育的初始内禀属性并未包括判断学生的知识状态、预测学生未来的学习表现等功能。

基于上述原因，知识追踪（Knowledge Tracing，KT）成了智慧教育领域的重要研究内容，它通过分析平台收集的学习行为数据判断学生的知识状态，并根据知识状态预测学生未来作答的表现。知识追踪目前被广泛应用于各类在线教育平台，如国家高等教育智慧教育平台、学堂在线、爱学习以及国外的Khan Academy、edX、Coursera 等。当前知识追踪的主要意义和作用在于通过把握学生的知识状态和未来的答题表现，为智慧教育平台提供细粒度的教育策略，为每个学生提供个性化的教育服务。

学习序列由学生的学习记录组成，主要包括学生的学习行为数据。学习行为数据一般可分为学习过程、学习结束和学习间隔数据三类［1］。学习过程数据主要包括学生尝试作答次数和请求提示次数等；学习结束数据主要包括学生作答的习题及作答的结果等；学习间隔数据主要包括学生相邻两次学习的时间间隔和学习某概念的次数等。图1 展示了学习过程行为、学习结束行为和学习间隔行为及其先后关系。

图1 学习行为及其先后关系Fig.1 Learning behaviors and their sequential relationship

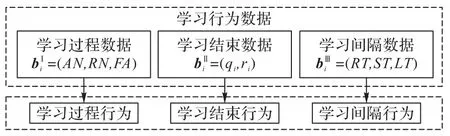
图2 学习行为及其数据的对应关系Fig.2 Correspondence between learning behaviors and their data

经典的知识追踪模型［2-4］仅使用学习结束数据。这类模型一般通过分析学生的学习结束行为判断学生的基本知识状态，但学习结束数据只包含了学生答对或答错某道习题的信息，无法更加准确地追踪学生的知识状态。例如，学生A、B 的学习结束数据相同，但学习过程数据不同，在经典知识追踪模型中无法表示学生A、B 不同的知识状态。

学生的学习记录中还包括学习过程行为和学习间隔行为，这些行为也是学生知识状态发生变化的映射。有研究者利用学习过程和学习结束数据追踪学生的知识状态［5］，用学习间隔数据建模学生的遗忘行为［6-7］，但都没有考虑学习行为的多类协同性，即学习序列中多种类型学习行为的相互作用。

为了更加准确地追踪学生的知识状态，本文的主要工作有：

1）描述学习行为的同类约束性。首先，选取三类学习行为数据的集合作为输入；然后用多头注意力机制获取输入数据的注意力权重，表示单一类型学习行为在时间序列上的约束关系，用来描述学习行为的同类约束性。

2）描述学习行为的多类协同性。首先，拼接三类学习行为数据的集合作为输入；接着用通道注意力机制获取三类学习行为的全局信息；最后将全局信息映射为学习行为之间的注意力权重，表示多种类型学习行为的相互作用，用来描述学习行为的多类协同性。

3）提出多学习行为协同的知识追踪（Multi-Learning Behavior collaborated Knowledge Tracing，MLB-KT）模型。首先，使用编码器融合学习行为的同类约束性和学习行为的多类协同性；然后使用解码器通过输入不同的查询向量来获取学生的学习向量和遗忘向量；最终达到更准确地追踪学生知识状态的目的。

1 相关工作

1.1 知识追踪

1.1.1 基于学习结束行为的知识追踪模型

贝叶斯知识追踪（Bayesian Knowledge Tracing，BKT）［2］首先提出知识追踪的概念，并用概率计算解决知识追踪的任务。BKT 以学习结束数据为输入，定义初始学会某概念的概率P(L0)、未学会状态到学会状态的转移概率P(T)、未掌握概念但猜对的概率P(G)、掌握概念但答错的概率P(S)等，并使用隐马尔可夫模型（Hidden Markov Model，HMM）［8］建模上述四个概率的关系，从而预测学生的未来学习表现。

深度知识追踪（Deep Knowledge Tracing，DKT）［3］首次使用深度序列模型来解决知识追踪的任务。类似于BKT，DKT仍使用学习结束数据作为输入，以循环神经网络（Recurrent Neural Network，RNN）［9］或长短 期记忆（Long Short-Term Memory，LSTM）网络［10］的隐藏状态来表示学生的知识状态，最终以全连接层预测学生的未来学习表现。

动态键值记忆网络（Dynamic Key-Value Memory Network，DKVMN）［4］受标准记忆增强网络的启发［11］，提出用记忆矩阵的方法解决知识追踪的任务。DKVMN 仍使用学习结束数据作为输入，用一个键（key）矩阵存储概念，一个值（value）矩阵存储学生对概念的掌握状态；模型通过两个矩阵判断学生每次学习时对各个概念的掌握状态，最终以全连接层输出学生未来学习表现的概率。

在后续的研究中，研究者仍仅用学习结束数据作为模型的输入建模学生的知识状态：Käser 等［12］在BKT 的基础上提出了动态贝叶斯知识追踪模型，建模不同概念之间的依赖关系；Su 等［13］在DKT 的基础上为模型的输入添加了习题信息；Abdelrahman 等［14］在DKVMN 的 基础上使用了Hop-LSTM 网络结构，使模型能够捕获学生学习记录中的长期约束性。这类模型的变种还有：TLS-BKT（Three Learning States Bayesian Knowledge Tracing）［15-16］、PDKT-C（Prerequisite-driven Deep Knowledge Tracing with Constraint modeling）［17］、HMN（Hierarchical Memory Network for knowledge tracing）［18］等。

BKT、DKT 和DKVMN 是经典的知识追踪模型，这些模型为后续的研究奠定了坚实的基础；但它们在追踪学生的知识状态时仅用学习结束数据建模学习行为的同类约束性，没有使用学习过程数据和学习间隔数据建模学习行为的多类协同性，所以无法为表示学生的知识状态提供更加充分的支撑。

1.1.2 基于学习间隔行为的知识追踪模型

部分研究用到了学习间隔数据：Nagatani 等［6］受艾宾浩斯遗忘曲线［19］的启发，在DKT 模型的基础上增加了学习间隔数据作为输入，他们认为学习间隔数据是影响遗忘行为的因素，通过向模型增加学习间隔数据作为输入能够建模遗忘行为，提出了DKT-F（DKT+Forgetting）模型；李晓光等［7］受艾宾浩斯遗忘曲线和记忆痕迹衰退说［19-20］的启发，提出了学习与遗忘融合的深度知识追踪模型，该模型不仅考虑了上述学习间隔数据，还考虑了学生概念掌握状态对遗忘的影响。

虽然上述两个模型在使用学习结束数据的基础上增加了学习间隔数据并取得了较好的效果，但仍仅建模学习行为的同类约束性，忽略了建模学习行为的多类协同性。

1.1.3 基于学习过程行为的知识追踪模型

部分研究用到了学习过程数据：Cheung 等［5］用学习过程数据输入分类和回归树模型预测学生能否正确作答习题，然后将预测结果与真实结果组合，最后将组合的数据与学习结束数据输入DKT 模型预测未来答题情况，提出了DKT-DT（Deep Knowledge Tracing with Decision Trees）模型。该方法将学习过程数据作为学习结束数据的一种补充，改进建模学习行为同类约束性的方法，但尚未建模学习行为的多类协同性。

总的来说，大部分研究在追踪学生的知识状态时仅用学习结束数据作为输入，或引入两种类型的学习行为数据作为输入，也有引入全部三种类型学习行为数据作为输入［21］，但均未建模学习行为的多类协同性。针对上述问题，本文提出了多学习行为协同的知识追踪模型，在建模学习行为同类约束性的同时，对学习行为的多类协同性也进行建模，为表示学生的知识状态提供更充分的支撑。

1.2 注意力机制

从生物学的角度看待注意力机制，它的原理是人类基于非自主性提示（Nonvolitional cue）和自主性提示（Volitional cue）有选择地引导注意力的焦点［22］。非自主性提示指的是人没有认知和意识的驱动来获取信息；自主性提示指的是人有认知和意识的驱动来获取信息，其中，查询是自主性提示，键和值是非自主性提示。添加自主性提示的好处是使注意力机制的输出偏向于某些输入数据，而不是对输入数据全盘接收。

例如在判断学生的知识状态时，学生S 在某次学习中答对了有关概念C 的习题。如果没有认知和意识的驱动，仅以学习结束数据为标准，教师的注意力由非自主性提示引导并判断学生S 对概念C 的掌握状态；但如果有了认知和意识的驱动，在学习结束数据的基础上，教师还会注意到学生的学习过程数据和学习间隔数据，注意力由自主性提示引导并判断学生S 对概念C 的掌握状态。

Ghosh 等［23］提出了 AKT（context-aware Attentive Knowledge Tracing）模型，用注意力机制构建习题qt和结果rt的上下文感知表示，总结学生过去的表现来解决知识追踪任务。邵小萌等［24］提出融合注意力机制的时间卷积知识追踪（Temporal Convolutional Knowledge Tracing with Attention mechanism，ATCKT）模型，用注意力机制建模学生学习的习题对各时刻知识状态不同程度的影响。注意力机制的输入是查询（query）、键（key）以及值（value），输出是值的加权和，注意力权重通过计算查询和键的相似度获得。自注意力机制是注意力机制的变体，它的输入来自同一数据，由于没有外部数据的输入，所以更擅长捕捉数据内部的相似性，减少了对外 部数据 的依赖。Pandey 等［25］提出了SAKT（Self-Attentive model for Knowledge Tracing）模 型，首次将Transformer 模型［26］应用到知识追踪领域，通过描述输入在时序上的约束关系来完成知识追踪任务。Transformer 模型的主要结构是多头注意力机制，由多个注意力机制或自注意力机制并行组成，其中的全连接层将输入数据映射到不同的子空间，能够基于相同的机制学习到不同的权重，用来描述学习行为的同类约束性。

多头注意力机制使用学习过程、学习结束以及学习间隔数据作为自主性提示，它的缺点在于不同的学习行为在追踪知识状态时被视作具有相同的权重。通道注意力机制能解决这一问题［27-30］，将三类学习行为数据作为通道注意力机制的输入，“挤压”操作收集三类学习行为数据的全局信息，“激励”操作将全局信息转化为注意力权重，表示多种类型学习行为的相互作用，用来描述学习行为的多类协同性。

2 多学习行为协同的知识追踪模型

2.1 模型提出的思想

学习序列包括不同类型的学习行为，如学习过程、学习结束、学习间隔等行为。本文使用学习过程数据bI、学习结束数据bII、学习间隔数据bIII分别描述上述三类学习行为，其中：bI主要包括学生的尝试作答次数和请求提示次数等数据；bII主要包括学生作答的习题及作答的结果等数据；bIII主要包括学生相邻两次学习的时间间隔和学习某概念的次数等数据。我们发现，学习行为具备同类约束性和多类协同性的特征。具体说明如下：

根据文献［31］，学生知识状态的变化受其已有知识状态的约束，表现为学习行为的同类约束性，即知识状态的变化在某一学习行为上的反应是平缓的。具体地，学习过程数据bI的同类约束性可能表现在，针对某一习题学生的尝试作答次数在相邻时间步的变化是平缓的；学习结束数据bII的同类约束性可能表现在，针对某一习题学生的作答结果的变化也是平缓的；学习间隔数据bIII的同类约束性可能表现在，若干次相邻的学习时间间隔的变化同样是平缓的。从模型角度上来说，对三类学习行为数据的表征应考虑其各自的同类约束性，以此来反映学生知识状态的客观变化，这是当前研究所忽略的。

根据文献［32］，学习序列中多种类型学习行为存在相互作用，表现为学习行为的多类协同性。具体地，学习过程数据bI和学习结束数据bII的多类协同性可能表现在，针对某一习题学生尝试作答次数较多时作答结果正确的概率较低，尝试作答次数较少时作答结果正确的概率较高；学习间隔数据bIII和学习结束数据bII的多类协同性可能表现在，针对某一习题学生学习时间间隔较长时作答结果正确的概率较低，学习时间间隔较短时作答结果正确的概率较高。从模型角度上来说，对三类学习行为数据的表征应考虑其多类协同性，以此来反映学生知识状态的客观变化，这是当前研究所忽略的。

BKT 使用学习结束数据bII追踪学生的知识状态。但bII只包含了学生答对或答错某道习题的信息，且没有表示出学习结束行为在时间序列上的约束关系，即学习结束行为的约束性。虽然后续的研究［12-15］仍旧仅使用学习结束数据bII，但多使用深度模型，所以在建模学习结束行为的约束性方面有一定的进展。随后，部分研究者向模型的输入增加学习过程数据bI［5］和学习间隔数据bIII［6-7］，提高了模型的性能。虽然这些研究验证了学习过程和学习间隔行为的有效性，但是没有建模出学习序列中多种类型学习行为的相互作用，即学习行为的多类协同性。

综上所述，在追踪学生的知识状态时，综合考虑多类学习行为数据是有利的，这能使知识追踪模型更准确地预测学生的未来表现。然而在建模学习行为时，应综合考虑学习行为的同类约束性和多类协同性。

本文使用多头注意力机制自适应地分配每类学习行为数据自身的权重，以此建模学习行为的同类约束性；使用通道注意力机制自适应地分配不同类型学习行为数据之间的权重，以此建模学习行为的多类协同性。

2.2 学习行为数据定义

2.3 多学习行为协同的知识追踪模型架构

本文提出了多学习行为协同的知识追踪（MLB-KT）模型，整体流程如图3 所示。MLB-KT 模型由输入模块、编码器、解码器以及预测模块组成：输入模块嵌入表示若干连续的学习行为数据；编码器建模学习行为的同类约束性和多类协同性；解码器生成学生的学习和遗忘向量，并更新状态矩阵图3 中的虚线表示预测模块根据前一时刻的状态矩阵、概念矩阵以及当前时刻作答的习题qt预测学生的答题情况；Mk表示概念，Mv表示学生的概念掌握状态，这两个矩阵随着学习序列而动态更新。

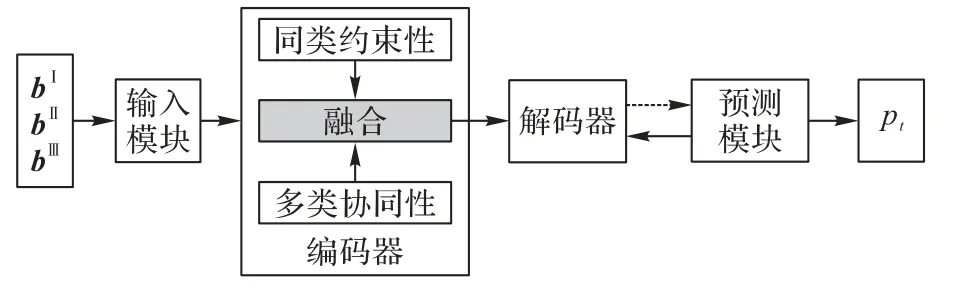
图3 MLB-KT模型的整体流程Fig.3 Overall flowchart of MLB-KT model

2.3.1 输入模块

取连续n条嵌入表示的学习行为数据，再根据学习行为类型分别组合得到3 个大小为n×dv的矩阵BI、BII、BIII作为多头注意力机制的输入；将这3 个矩阵拼接成一个大小为3 ×n×dv的三维数组Xt作为通道注意力机制的输入，其中3表示数组Xt包含三类学习行为；n表示数组Xt包含连续n条学习行为；dv是学习行为数据向量表示的维度。图4 展示了输入模块的设计细节。

图4 输入模块Fig.4 Input module

2.3.2 编码器

数组Xt由矩阵BI、BII、BIII拼接组成，这三个矩阵各自均包括了n条连续的学习行为数据，这些学习行为数据分别表示三类不同的学习行为：学习过程、学习结束和学习间隔等行为。

1）建模同类约束性。每一类学习行为在学习序列上均存在对后续同类行为的约束性，即学习序列中相同类型学习行为在时间序列上的约束关系。因为多头注意力机制能够定位学习序列上的相似信息，并转化为序列中学习记录的相对权重，所以使用多头注意力机制来建模上述同类约束性，具体流程如图5 所示，其中h表示多头注意力机制的层数。

图5 建模同类约束性Fig.5 Modeling homo-type constraint

首先使用参数v∈R1×n作为位置编码，表示连续n条学习行为数据在时序上的相对位置，加入到输入矩阵BI、BII、BIII中，形成含有时序上相对位置信息的学习行为矩阵：

其次将学习行为矩阵BI*、BII*和BIII*分别输入多头注意力机制，通过计算各学习行为间的相似性获得注意力权重，用于建模学习行为的同类约束性，注意力权重的大小表示学习行为约束关系的强弱。输出矩阵和分别表示学习过程行为、学习结束行为以及学习间隔行为的同类约束性：

2）建模多类协同性。多类学习行为之间存在相互的协同性，即学习序列中多种类型学习行为的相互作用。因为通道注意力机制能够捕获多种类型学习行为的全局信息，并转化为各个学习行为的相对权重，所以使用通道注意力机制建模学习行为的多类协同性，具体流程如图6 所示。

图6 建模多类协同性Fig.6 Modeling multi-type collaboration

将数组Xt作为通道注意力机制的输入，通过收集三类学习行为的全局信息进而获得注意力权重，用于建模学习行为的多类协同性，注意力权重的大小表示学习行为协同的程度。挤压（squeeze）操作收集学习行为的全局信息，激励（excitation）操作通过全连接层将上述全局信息转化为不同学习行为间的注意力权重s：

其中：Sigmoid(xi)=1/(1+)；全连接层的权重矩阵为W；RC(·)表示逐行卷积；Cov(·)表示计算协方差矩阵，协方差矩阵用来表征三类学习行为的相关程度。

输出的注意力权重s表示学习行为的多类协同性，将其与数组Xt进行通道乘法，改变数组Xt特征值的表达，得到数组XC：

将表示学习行为同类约束性的数组XB和表示学习行为多类协同性的数组XC相加得到数组X＇，通过全局平均池化获得学习行为同类约束性和多类协同性的全局信息：

将全局信息向量g∈R1×3用线性整流函数（Rectified Linear Unit，ReLU）激活，得到特征向量z∈

其中：ReLU(x)=max(0，x)；Wz∈。向量z用于生成同类约束性数组XB和多类协同性数组XC的融合权重：

其中：αB∈R1×3、αC∈R1×3是同类约束性数组XB和多类协同性数组XC的融合权重；R∈、Q∈表示数组XB和数组XC的软注意力矩阵。

加权融合同类约束性数组XB和多类协同性数组XC，并用3 × 1 ×dv的卷积核对融合数组进行逐行卷积，得到编码器的输出XE∈表示学习行为的同类约束性和多类协同性：

2.3.3 解码器

解码器由两个h层的多头注意力机制组成，通过矩阵XE分别生成学习向量和遗忘向量，结构如图7 所示。首先，以第t次学习结束数据作为查询输入，从h个空间维度表示学习向量lt；其次，以第t次学习间隔数据作为查询输入，从h个空间维度表示遗忘向量ft；最后，根据向量lt和ft更新概念掌握状态矩阵Mv。

图7 解码器Fig.7 Decoder

将矩阵XE输入Tanh 函数激活的全连接层获得解码向量ut∈，是矩阵XE的降维表达：

其中：Tanh(xi)=Wu、bu分别是全连接层的权重矩阵和偏置项。解码向量ut含有学习行为的同类约束性和多类协同性，将其作为图6 中多头注意力机制L、F 中键和值的输入。

在多头注意力机制L 中，以向量作为查询输入，获得学习向量lt：

在多头注意力机制F 中，以向量作为查询输入，获得遗忘向量ft：

其中：WF、bF分别是全连接层的权重矩阵和偏置项。向量是经过处理后的学习间隔数据，该向量描述的是学生相邻两次学习的时间间隔和学习某概念的次数等学习行为，用它做解码过程的查询输入可以得到学生因遗忘而引起的概念掌握状态的变化情况。

学习向量lt和遗忘向量ft以及关联权重wt用于更新当前时刻的概念状态矩阵

关联权重wt将在预测模块中描述。

2.3.4 预测模块

预测模块用于预测学生未来的答题情况，结构如图8所示。

图8 预测模块Fig.8 Prediction module

首先，将习题qt转换为one-hot 编码，与嵌入矩阵A∈相乘，得到维度为dk的习题嵌入向量kt，描述习题qt的相关信息。

其次，将kt与存储概念的矩阵Mk∈相乘，并通过Softmax 函数转化为关联权重wt，用来描述习题qt所包含的概念。

然后，将关联权重wt与矩阵相乘，得到向量nt，表示学生对习题qt所包含概念的掌握状态：

考虑到习题间存在一定的差异，如难度系数不同，将向量nt与向量kt进行拼接，并输入至带Tanh 激活函数的全连接层，得到向量it。向量it既包含了学生对概念的掌握状态又包含了习题信息：

最后，利用一个带有Sigmoid 激活函数的输出层，将it作为输入，用来预测学生对习题qt的表现情况：

2.4 损失函数

本文选择交叉熵损失函数来最小化预测值pt和真实标签rt之间的差异性。

3 实验与结果分析

3.1 数据集和实验环境

本文相关实验在3 个真实数据集ASSISTments2012（简记 为Assist12），ASSISTments2017（简记为Assist17）和JunyiAcademy（简记为Junyi）上进行，其中，每个数据集70%的数据作为训练集，30%的数据作为测试集。上述数据集的基本信息如表1 所示，包括学生数、学习记录数以及概念数。本文实验具体软硬件配置如表2 所示。

表1 数据集的基本信息Tab.1 Basic information of datasets

表2 实验环境Tab.2 Experimental environment

3.2 模型性能对比

使用曲线下面积（Area Under Curve，AUC）分析和评价MLB-KT 模型的性能。AUC 是受试者工作特征曲线（Receiver Operating Characteristic curve，ROC 曲线）与横坐标轴围成图形的面积，该面积的取值为［0.5，1］，若AUC 的值为0.5，说明模型是随机预测模型；AUC 的值越大，说明模型预测性能越好。

MLB-KT 模型的核心是以三类学习行为作为输入，使用多头和通道注意力机制分别建模上述学习行为的同类约束性和多类协同性。基于上述情况，在选择对比模型时本文主要考虑如下三个条件：一是被广泛接受且性能表现属同类最好的模型；二是输入各类学习行为数据的模型；三是建模同类约束性或多类协同性的模型。

根据上述三个条件，本文选用的对比模型为：仅使用学习结束数据作为输入的单学习行为模型DKT［3］、DKVMN［4］、ATCKT［24］、SAKT［25］以及CL4KT（Contrastive Learning framework for KT）［33］；在使用学习结束数据作为输入的基础上，引入其他学习行为数据的多学习行为模型DKT-DT［5］、DKT-F［6］。主要原因在于，这些模型均以部分或全部学习行为数据为输入，并建模了同类约束性或多类协同性。具体地，DKT、DKVMN 和CL4KT 使用学习结束数据作为输入，使用序列模型建模同类约束性；SAKT 和ATCKT 同样使用学习结束数据作为输入，还使用注意力机制建模同类约束性；DKT-F 和DKT-DT 在使用学习结束数据的基础上，分别增加了学习间隔和学习过程数据作为输入，使用序列模型建模同类约束性，未建模多类协同性。性能对比实验的结果如表3所示。

表3 不同模型的AUC对比Tab.3 AUC comparison of different models

单学习行为模型中的ATCKT 在三个真实数据集上的AUC 值分别到达了0.762、0.793 和0.847，属同类最高，整体表现良好，5 个单学习行为模型虽均使用学习结束数据作为输入，但由于建模学习行为同类约束性的方法不同，模型性能存在差异。

多学习行为模型中的DKT-F、DKT-DT 引入其他学习行为数据作为输入，虽未改进建模学习行为同类约束性的方法，但改进了模型的输入，与单学习行为模型相比均有更好的表现。与DKT 和ATCKT 模型相比，MLB-KT 在Assist17 数据集上的AUC 值分别提升了12.26%、2.77%，且MLB-KT 的AUC 值在3 个真实数据集上均优于其他模型，分别达到了0.768、0.815 和0.864，说明了在建模学习行为同类约束性的基础上建模多类协同性的有效性。

3.3 学习行为对比

模型性能对比结果表明引入其他学习行为数据作为输入能够带来模型性能的提升。为了进一步对比分析三类学习行为在模型中的重要程度，本文调整缺省MLB-KT 模型的输入：MLB-e 表示模型仅以学习结束数据bII作为输入；MLB-pe 表示模型以学习过程数据bI和学习结束数据bII作为输入；MLB-ei 表示模型以学习结束数据bII和学习间隔数据bIII作为输入。表4 给出了上述模型以及它们在3 个数据集上的AUC 值。

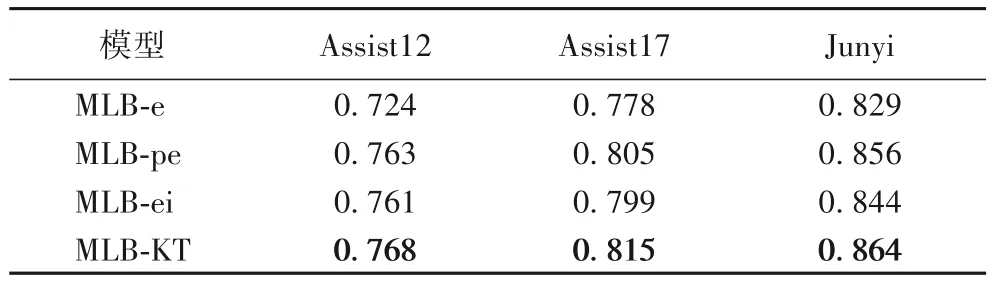
表4 不同输入数据对模型AUC的影响Tab.4 Influence of different input data on AUC of model

由表4 可以看出，在3 个真实数据集上，MLB-e 模型的AUC 最低，说明仅分析学习结束行为及其同类约束性能够基本判断学生的知识状态，但由于bII仅包含学生答对或答错的学习结束数据，包含的信息有限，无法更准确地建模同类约束性；MLB-pe 和MLB-ei 模型的AUC 值高于MLB-e，说明在将学习结束数据作为输入的基础上，还引入其他学习行为数据作为输入，并同时建模学习行为的同类约束性和多类协同性能够提高模型的性能；但这两个模型的AUC 值低于MLB-KT，说明在建模学习行为同类约束性和多类协同性的基础上，模型分析的学习行为越全面则模型的性能越高。

3.4 编码器消融

为了分析学习行为的同类约束性和多类协同性，本文分别熔断编码器中建模同类约束性和多类协同性的注意力机制：MLB-B 表示模型仅建模了学习行为的同类约束性；MLB-C 表示模型仅建模了学习行为的多类协同性。表5 给出了上述模型以及它们在3 个数据集上的AUC 值。由表5可以看出，MLB-KT 模型在3 个数据集上的AUC 值均优于其他两个模型，说明在综合考虑三类学习行为时分析其同类约束性和多类协同性是有效的；MLB-C 模型在三个数据集上的AUC 值要低于MLB-B 模型，说明仅建模学习行为的多类协同性而忽略同类约束性，会导致模型丢失学习行为在时间序列上的约束关系，无法提高模型的性能；而MLB-B 模型在三个真实数据集上的AUC 值要低于MLB-KT 模型，说明仅建模学习行为的同类约束性而忽略多类协同性，会导致模型丢失多种类型学习行为的相互作用，同样也无法提升模型的性能。

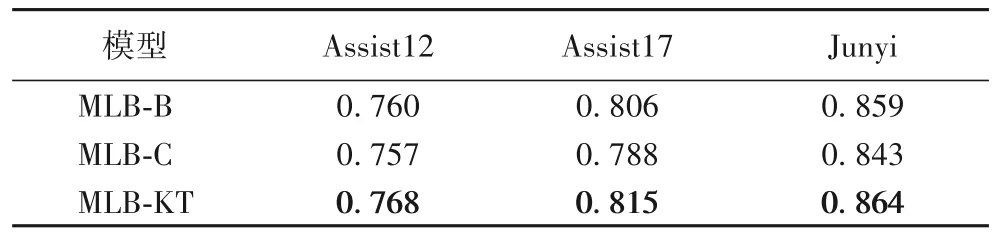
表5 编码器的消融实验结果Tab.5 Ablation experiment result of encoder

3.5 模型表示质量对比

模型的表示质量指模型在实际应用中预测结果与实际结果的总体差异情况。例如，知识追踪模型KT 由某个真实数据集训练且具有良好的预测性能。现将KT 应用于实际教学环境中，若KT 预测有40%的学生答错有关概念C 的习题，但实际结果显示只有10%的学生答错有关概念C 的习题，这表明KT 在实际应用中的预测结果与实际结果总体差异较大，表示质量有待提高。

上述示例中KT 虽然有良好的预测性能，但实际应用的表现情况较差，无法在实际教学环境中应用，这表明模型既需要较高的预测性能，同时其表示的质量也至关重要。一般使用校准曲线［33］测量预测概率和观测概率之间的一致性，使用基准对齐线x=y衡量各个模型的表示质量，校准曲线更贴近基准对齐线则说明模型预测概率更加接近观测概率，即模型的表示质量较好。

为了更好地展示模型与基准对齐线的距离，本文取模型的校准曲线与基准对齐线的差值，得到差值对齐线y=0（Baseline），模型的校准曲线与差值对齐线越接近则表示模型的表示质量越好。图9 是各个模型的校准曲线与差值对齐线的位置关系（以Assist12 为例）。

图9 各个模型的校准曲线与差值对齐线的位置关系（以Assist12为例）Fig.9 Position relation between calibration curve of each model and difference alignment line（taking Assist12 as an example）

如图9 所示，首先，无论在观测概率较低还是观测概率较高时，MLB-KT 模型差值线都更接近基准线，说明在与对比模型的比较中，MLB-KT 模型的表示质量更优。其次，SAKT、ATCKT 以及CL4KT 模型的差值线虽也接近基准线，但这些模型的差值线相较于MLB-KT 的差值线表现出更为剧烈的起伏，即整体上看，MLB-KT 模型的表示质量较为稳定。图9 的结果表明，MLB-KT 考虑多种学习行为并建模学习行为的同类约束性和多类协同性是有效的，这使模型不会显示严重的偏差，并获得更好的表示。

4 结语

本文提出了一个多学习行为协同的知识追踪模型MLBKT，用于解决现存知识追踪模型无法准确地描述单一类型学习行为在时间序列上的约束关系，或无法准确地描述多种类型学习行为相互作用的问题。MLB-KT 模型使用多头注意力机制表示学习行为的同类约束性；使用通道注意力机制表示学习行为的多类协同性；融合同类约束性和多类协同性，完成对不同类型学习行为的协同表示。MLB-KT 模型与7 个对比模型在3 个真实数据集上的实验结果显示，MLB-KT 模型性能较为突出，同时验证了同类约束性和多类协同性的有效性，而且本文的模型在表示质量方面也优于对比模型。未来将继续深入研究学习行为的同类约束性和多类协同性对知识追踪模型带来的影响。