基于事件触发机制的神经网络同步控制

葛 超，常晨蕾，姚 征，苏 皓，2

（1.华北理工大学 电气工程学院，河北 唐山 063210；2.华北理工大学 唐山市半导体集成电路重点实验室，河北 唐山 063210）

0 引言

神经网络（Neural Network，NN）是一种典型的神经元互连形成的复杂系统，表达一种类似于人脑的思维计算过程，因此，被广泛用作计算工具。在过去的十几年中，NN 已被应用于生物系统、化学反应、组合优化等领域［1-3］。但是在实际的应用中，不可避免地会出现时滞［4-6］、攻击［7-9］等问题，导致系统性能恶化，不稳定的情况也时有发生。例如，文献［10］中研究了一类具有离散时滞的神经网络控制，构造了一个新颖的泛函，利用杰森不等式处理积分项，推导其稳定性条件，由于杰森不等式涉及的信息较少，结果保守性较大。文献［11］中研究了在线性系统中控制器增益摄动存在的情况和离散时滞对线性系统性能的影响，利用杰森不等式来处理泛函求导过程中的积分不等式缩放问题，但该方法使系统过于理想化。

另外，大多数的系统都进行周期采样，传统的采样会传输所有的采样数据，导致资源浪费。为了解决资源浪费的问题，提出了一种新的触发机制——事件触发机制［12-14］，只有满足设定的触发条件，采样数据才会被传输。因此，事件触发机制的提出具有重大意义。文献［15］中同时考虑了连续时间和离散时间事件检测器，减少了资源的浪费，但是没有考虑到非脆弱对控制器的影响。文献［16］中考虑了离散和分布时滞对系统的影响，并且构造了一个新颖的李雅普诺夫泛函；但它采用周期采样，没有考虑事件触发机制，因此仍会发生资源浪费的现象。

受上述工作的启发，本文研究了一类在采样控制下具有离散和分布时滞的神经网络指数同步问题。使用一个具有伯努利分布的变量来描述控制器增益摄动的发生是随机的。利用采样时刻锯齿波信息，提出了一个新颖的双边泛函，并利用改进的不等式和凸优化来处理积分问题，得到了保守性较低的稳定性准则。

1 问题描述和事件触发机制

1.1 问题描述

考虑具有混合时滞神经网络的系统模型：

将式（1）视为主系统，则它的从系统可以用式（2）表示：

在实际应用中，不能保证所有的状态变量到控制器的信号都是连续的，所以本文考虑采样控制系统，u(t)为控制输入，采样瞬间为0 ＜t1＜t2＜… ＜tk＜tk+1＜… ＜∞，在传感器上成功传输的采样序列表示为γ={0，t1h，t2h，…，tkh}，h为采样周期，定义r(t)=y(t) -x(t)，进而得到主从同步误差系统：

其中：f(r(t))=g(y(t)) -g(x(t))。

考虑到控制器参数摄动，本文构造如下非脆弱控制器：

其中：K为控制器增益矩阵；ΔK(t)为控制器增益摄动，满足ΔK(t)=HF(t)B，H、B为常数矩阵，F(t)是未知矩阵，满足FT(t)F(t) ＜I；φ(t)满足伯努利分布，见式（5）。

当φ∈[0，1]，可以获得：

1.2 事件触发机制

本文引入事件触发机制，确定采样数据是否通过事件触发传输方案在通信网络上进行传输，通过事件发生器检测采样瞬间与最后触发的时间之间的采样数据误差。

事件触发条件定义为：

其中：e(ikh)=r(ikh) -r(tkh)，表示状态误差；ikh=tkh+ςh(ς∈N)表示当前采样时刻；r(tkh) ≜r(t-τ(t)) -e(ikh)，并且λ∈(0，1)为常数；ψ为正的加权矩阵。当满足式（7）时，将生成一个传输事件。

将零阶保持器中的保持间隔划分为一个子集Mζ=[ikh+τk，ikh+h+τk+1]，M=∪Mζ(ζ=0，1，2，…)。其 中：τ(t)=t-ikh，t∈Mζ。则式（4）被改写为：

当t∈Mζ，分段线性函数满足以下条件：

事件触发机制比传统的时间触发机制节省网络资源，它不需要连续检测。另外，最小传输间隔包含至少一个采样周期，防止芝诺行为的发生。

将控制器式（4）代入系统式（3）中，可得到如下同步误差系统模型：

本文的目的是考虑非脆弱的控制器参数摄动，设计非脆弱控制器，使误差系统稳定，进而实现主从同步控制。

1.3 引理、定义及假设

引理1［17］存在对称矩阵M和适当维数矩阵Y1、Y2，对于所有连续可微函数，满足以下不等式条件：

引理3存在一个矩阵H满足H=HT，具有相同维度的矩阵U1、U2，以下不等式成立：

对于所有满足FT(t)F(t) ≤I，则存在一个标量ρ＞0，使以下不等式成立：

定义1如果误差系统式（10）是指数稳定的，则主系统式（1）和从系统式（2）将实现指数同步。存在两个常数α和β使

2 控制器设计

本章建立了与时滞相关的指数稳定条件。为了简化书写，定义了以下式子，其中：diag {…}为对角矩阵，I表示有适当维数的单位阵。

考虑控制器存在参数摄动的情况，通过以下定理得到控制器的设计方法。

定 理1给定标 量λ∈(0，1)，τM＞0，d＞0，α＞0，φ＞0，ω1和ω2，如果存在矩阵P＞0，Rm＞0(m=1，2)，ψ＞ 0，Sm＞0(m=3，4)，Zm＞0(m=1，2，3)，Vm＞0(m=1，2)，Q＞0，G、L、S1、S2、M1、M2、Y1、Y2是具有合适维度的矩阵，则在非脆弱控制器式（4）下，保证误差系统的稳定，从而实现主系统式（1）和从系统式（2）的指数同步。

其中：定义Sym{A}=A+AT；row {…}为矩阵的行。

此外，本文设计的采样控制器增益矩阵可以通过K=G-1L给出。

证明

对泛函进行求导，得到如下结果：

由引理2 可以得到：

根据假设1，对于任何合适的对角线矩阵V1、V2，都可以获得如下不等式：

给定标量ω1、ω2和适当维数矩阵G，利用自由加权矩阵技术和式（6），很容易得到：

联合式（11），得到：

由于定理1 和文献［16］中的结论，可以很清楚地得到：

因此，给定正标量β，容易得到：

也可以等价为：

误差系统式（10）随衰减率α呈指数稳定，这表明主系统式（1）和从系统式（2）是呈指数同步的。

本文构造了一种新颖的泛函，不仅包括常规泛函，还包括双边泛函，S1、S2不一定是正定的，不仅考虑了区间[0，τ(t)]，还考虑了区间[τ(t)，τM]，推导出更严格的稳定性判据。

现在文献的工作中，大多数考虑在混合时滞下的非脆弱控制器同步控制，事件触发尚未在此领域得到充分发展，在定理1 中，提出了一种随机发生参数摄动的非脆弱控制器，服从伯努利分布。本文应用事件触发机制降低对网络资源的浪费，节省带宽，通过LMI 工具箱求得控制器增益矩阵K和触发参数ψ。

当控制器参数摄动消失时，可以得到如下的误差系统：

推 论1 给定标 量λ∈(0，1)，τM＞0，η＞0，d＞0，α＞0，ω1，ω2，存在矩 阵P＞0，Rm＞0(m=1，2)，ψ＞0，Sm＞0(m=3，4)，Zm＞0 (m=1，2，3)，Vm＞0 (m=1，2)，Q＞0；G，S1，S2，M1，M2，Y1，Y2是具有适当维数的矩阵，满足以下LMI：

在无参数摄动的控制器下，保证误差系统式（24）指数稳定从而实现主从同步。此外，采样控制器增益矩阵K通过K=G-1L给出。

该推论的证明过程和定理1 类似，故省略。

当系统简化为式（24）时，推论解决了文献［16］包含的问题，并且得到了比文献［16］更优的结果。它们的推论也很容易在本文中得到。

3 数值例子

例1 考虑以下参数时滞的神经网络：

误差状态响应如图1 所示，控制输入如图2 所示，可以看出误差系统最终趋于稳定，所设计的带有参数摄动的事件触发控制器是有效的。从图3 可以看出，当h=0.1，在8 s 内只需向控制器发送44 个采样信号，传输速率为55%，很容易看出，并不是所有信号都被传输。事件触发机制可以减少传输点的数量，以节省通信资源。

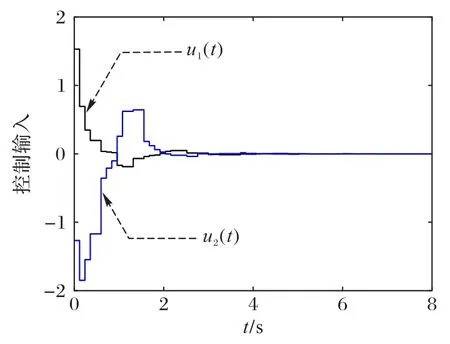
图2 例1的控制输入曲线Fig.2 Control input curve of example 1

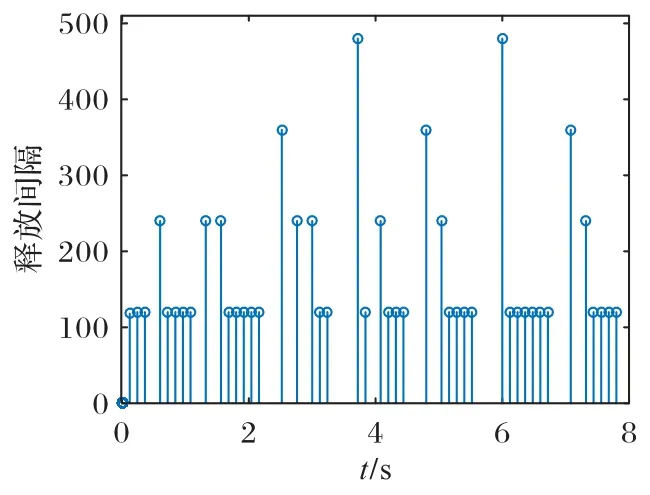
图3 例1的传输瞬间和释放间隔Fig.3 Transmission instants and release interval of example 1

例2 使用时滞神经网络系统的一个实际应用模型，称为四罐系统，参数如下：

在本例中不考虑非脆弱性，利用推论，事件触发机制被考虑为时间触发机制，当W4=0 时，可以得到最大的α为2.37，与文献［19］相比，指数衰减系数提升了0.16。控制器增益矩阵K为：

控制输入信号和误差状态响应信号如图4 和图5 所示。在图4 中，在控制器的作用下，误差信号迅速趋近于零，这说明本文提出的方法是有效的。

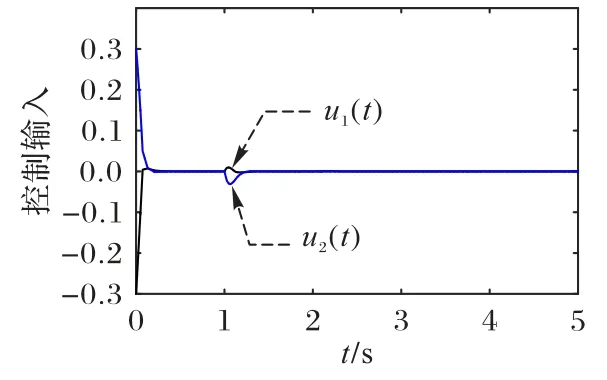
图4 例2的控制输入曲线Fig.4 Control input curve of example 2

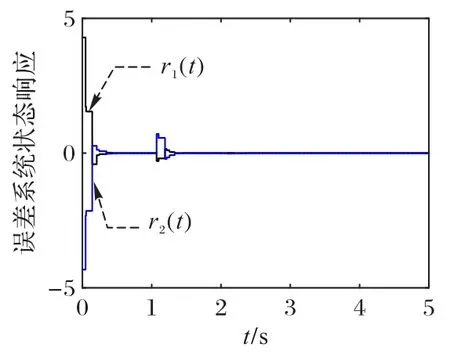
图5 例2误差系统状态响应曲线Fig.5 Error system state response curve of example 2

4 结语

本文研究了一类具有离散和分布式时滞的神经网络在非脆弱事件触发控制下的指数同步问题，提出了一种新的双边泛函，考虑了更多关于神经网络系统的状态特征信息。此外，利用改进的不等式和凸组合，得到了较不保守的同步准则。目前，基于动态事件触发的神经网络同步控制的研究还不够成熟，特别是动态事件触发的切换神经网络，是我们今后研究的主要内容。