航天器碰撞规避单脉冲切向控制最优策略
2023-05-12蔡立锋吴凌九张国云李冰冰孙振江
蔡立锋 吴凌九 张国云 李 智 李冰冰 孙振江
中国西安卫星测控中心,航天器在轨故障诊断与维修重点实验室,西安 710043
0 引言
随着低轨航天器日益增多,尤其是我国低轨互联网星座计划实施以后,在轨航天器的碰撞规避事件将快速增长[1-2]。这就要求地面卫星操控中心快速确定规避控制最优策略。由于卫星控制系统设计、载荷应用、测站可见性等约束,绝大多数规避控制均是实施一次单脉冲切向控制。单脉冲切向控制规避策略需要确定碰撞交会前的控制时刻和控制量两个变量,实现控后两星最近距离大于某一安全距离;其中控制时刻是由测控条件、卫星载荷应用需求、卫星平台工作状况、地面工作规划等诸多条件约束,控制量要求尽可能小,以减少燃料消耗,尽量少偏离卫星工作轨道。本文研究单脉冲切向碰撞规避最小控制量确定方法。
碰撞规避方式按照交会目标轨道测量手段分为近距离自主测量和地面测量两种。文献[3]研究了在地面预警的基础上,通过星上自主测量设备在交会前十几秒开始测量两星相对运动参数,通过机动改变交会时刻视线转率的方式规避碰撞风险,虽然近距离自主测量精度较高,但是轨道机动后轨道位置演化的时间太短,目前仍需要消耗更多的燃料,且会增加星上负担。所以目前碰撞规避仍是依赖地面测量数据提前较长时间进行规避机动的方式。
地面提前规避有高度规避方法和沿迹规避方法。文献[4-7]研究了受威胁卫星机动后自身在高度或沿迹方向上的变化,未考虑受威胁卫星不机动轨道、机动轨道、威胁目标三者在空间的位置关系,以及机动控制量与规避距离的单调性问题。文献[8]基于相对位置速度的线性方程研究了提前几轨点火机动的优化问题,但是对卫星的机动能力和燃料消耗要求较高。
规避策略的确定还涉及到碰撞风险评估方法问题,碰撞风险评估方法分为Box区域方法(Box Method)和碰撞概率两种方法。碰撞概率方法计算两目标碰撞的概率,需要获知两目标在交会时刻的位置误差协方差矩阵,通过减少碰撞概率进行规避策略的确定,理论上已有很多研究[9-13]。在实际工程应用中,仍主要采用Box区域方法作为规避控制安全门限。由于对空间目标的确定和预报均存在一定的误差,Box区域方法就是设定危险目标的接近范围,当最小接近距离小于该范围,就提前实施控制,使得最小接近距离大于该范围。本文推导了小偏心率轨道卫星切向控制后的轨道相对原轨道的相对运动方程,分析空间接近几何关系,给出Box区域方法限定的空间接近距离和交垂线方向距离约束情况下控制时刻对应的最小控制量的计算方法和函数曲线,证明控制量与规避距离的单调性关系,并讨论控制时刻对控制效果的敏感性。
1 控后相对运动方程
假设t0时刻获知某卫星A与空间飞行物体B有碰撞风险,在交会时刻ts最小接近距离为d,或者两星速度交垂线方向(两星交会时刻速度的叉乘方向)最小距离为h,小于对应的允许门限值d0或者h0,需要提前在tc时刻对A星实施单脉冲切向控制,以实现在交会点d≥d0或者h≥h0。设a、e、w和f分别为卫星轨道半长轴、偏心率、近地点辐角和真近点角,e1=ecosw,e2=esinw,卫星距升交点的角距为θ=w+f。假设在tc时刻,实施了切向脉冲控制,半长轴控制量为δa,则同时对轨道半长轴a和偏心率e的改变效果为[14]:
(1)
式中:θc为控制时刻的θ。定义卫星轨道坐标系oXYZ,Z轴由卫星质心指向地心,X轴在轨道平面内与Z轴垂直,指向卫星运动的方向,Y轴与Z、X轴成右手螺旋关系。设实施控制后的卫星为A1星,设A1相对于A星在A星轨道坐标系中相对位置为ρ=[xyz]T,则[15]:
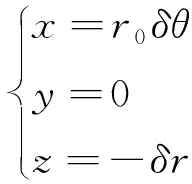
(2)
式中:r是卫星径向距离,r0是A星径向距离。设小偏心率情况下,e和地球带谐项J2同一量级,则式(2)θ展开式为:
θ=λ+2esinM+o(e2)=λ+
2e1sinλ-2e2cosλ+o(e2)
(3)
式中:λ=w+M,M为平近点角。一阶近似情况下,可以将式(2)中δθ和δr表示如下:
(4)
式中:a0是A星平半长轴。一般控制量δa为1km量级,一阶近似下δλ可以表示为:
(5)
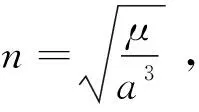
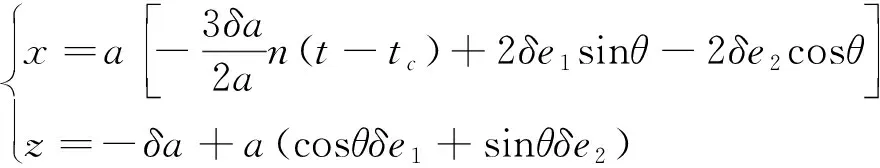
(6)
当t=ts,式(6)即为交会时刻ts时,A1与A星的相对位置。设θs为控交会时刻的θ值,u=θs-θc为从控制时刻tc到交会时刻ts卫星转过的角度,以下称相位差。将式(1)代入式(6),并利用近似关系n(ts-tc)=u,可得:

(7)
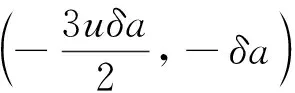
在A星轨道坐标系中观察,A星不动,飞行物体B与A星接近。对于绝大多数碰撞规避事件,相互接近的A、B两星星轨道面相差并不很小,在相互接近的短暂时间内,两星相对速度较大,可以视为在相互接近的几秒钟时间内,B在A星轨道坐标系中进行直线运动,则接近最小距离即为A星与该直线的最近距离。现在定义接近坐标系。设在互相接近的短暂时间内,A星的速度矢量为vA,B星的速度矢量为vB,定义接近坐标系oXjYjZj的Zj轴为vA×vB所确定的方向,Xj轴为vA确定的方向。接近坐标系是A星轨道坐标系绕Y轴转过一个角度β,使得新的X轴与vA重合,再绕新的Y轴旋转α角得到。设轨道坐标系到接近坐标系的转换矩阵为Loj,则:
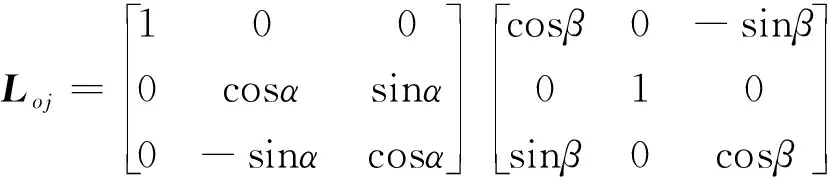
(8)
实际上β即为卫星沿轨道飞行的飞行角,可由开普勒根数表示为[14]:
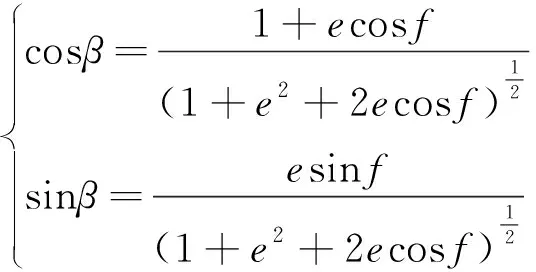
(9)
可见,在小偏心率情况下,cosβ≈1,sinβ=o(e)。角α可以由接近坐标系定义的方向余弦及式(9)确定的角β得到。
由式(7)可知,接近坐标系下,A1星相对于A星的位置向量PA1为:
(10)
式中:S为:
(11)
问题变为求解A1星相对于A星空间椭圆轨迹,与B星在接近坐标系中运动直线之间的最小距离的问题。
2 最优策略确定方法
2.1 最近距离约束情况下的最小控制量确定
B星相对于A的速度在惯性坐标系表示为vBi-vAi;设交会时刻A、B星在惯性系中的位置为分别为PAi、PBi,则B星相对于A星速度和位置转换到接近坐标系为:
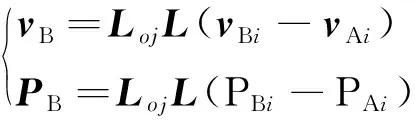
(12)
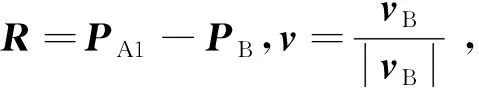
(13)
以下将d(u,δa)称为接近距离。允许的接近距离为d0,求解方程d-d0=0的根,即可求得对应的半长轴控制量δa和相位差u,相位差u对应着唯一的控制时刻tc。现固定某控制时刻,讨论对应的控制量与接近距离的关系。此时有:
(14)
定义函数撇号上标表示对δa求导,由式(10)可知R′=S,v随δa的变化与β角有关,由式(9)可知,小偏心率情况且δa为km量级情况下,可以近似认为v′=0,对式(14)的δa求导可得:
(15)
先对交会前一段时间的控制时刻进行遍历,通过式(14)和(15),使用牛顿迭代法可以很快计算得到满足d-d0=0的条件的每个控制时刻tc对应的控制量δau。
下面证明解的单调性。令式(15)的d′=0,对应的控制量为:
(16)
可见,极值δam是唯一的。设δam对应的接近距离为dm。由(dd′)′=d′d′+d″d可得在δam处,有:
(17)
式(17)说明d(δa)在δam处为最小值,仅当d>dm才有解δau,且一个d对应的解δau必然是成对出现的。规避控制的目标必然要求d≥d0>d(δau=0)≥dm。因此当控制量δa的绝对值|δa|大于|δau|时,其对应的接近距离d(δa)一定大于允许的接近距离d0,|δau|即是tc时刻控制且满足接近距离大于允许接近距离d0的最小控制量。
2.2 最近交垂线约束情况下的最小控制量确定
上面讨论了通过接近距离隔离,下面讨论通过交垂线距离隔离。空间交会接近的两颗卫星,在速度方向上误差传播较快,且误差较大;而与两颗卫星速度都垂直的方向上误差较小,因此交垂线方向隔离允许的最小距离较小。交垂线的方向即为接近坐标系中的Zj轴方向,设式(12)中PB的Zj分量为PBz,而A1星相对于A星在Zj方向的分量为式(10)的Zj分量,则A1星相对于B星在Zj方向的距离为:
(18)
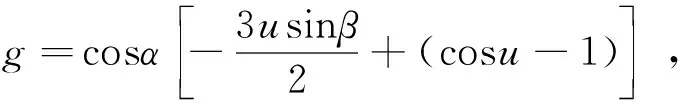
3 算例校验及控制时刻的敏感性分析
现在以一个算例来说明单批次切向脉冲最优规避策略的计算方法。设ts时刻A、B两星相对距离最近,A、B两星均为近圆轨道,轨道高度为500km附近。设B星在A星的接近坐标系中的相对位置和速度分别为PB=[PBxPByPBz]T,vB=[vBxvByvBz]T,如表1所示。

表1 两星碰撞预警信息
在接近坐标系中,A1星、A星和B星在交会点的空间几何关系如图1表示。图中A点表示A星的位置,B点表示B星的位置,波动曲线由式(10)确定,表示A1星在不同控制时刻tc对应的时间间隔ts-tc的位置变化,图中的A1点表示在交会时刻前24小时实施了半长轴增加0.05km的切向单脉冲控制后,A1星运行至交会点时刻的位置。在交会点附近,B星相对A星作直线运动,BC为B星的直线运动轨迹,AB⊥BC,是不控情况下,A、B两星的最近距离;CA1⊥BC,是提前24h时刻进行切向脉冲控制,半长轴增加0.05km情况下,A1、B两星的接近距离;A1点的坐标是(-7.08,0,-0.001)。由于BC与A星的切向运动方向夹角较小,所以虽然单脉冲控制情况下在切向方向改变了7.08km,但是接近距离仅为2.55km。如果两星相对运动方向夹角更小,会出现控制量已经很大,且很早实施了控制,仍不能在接近距离上规避碰撞风险的情况。有时候,可能更适合考虑在Zj方向即双星速度矢量的交垂线方向进行规避控制。
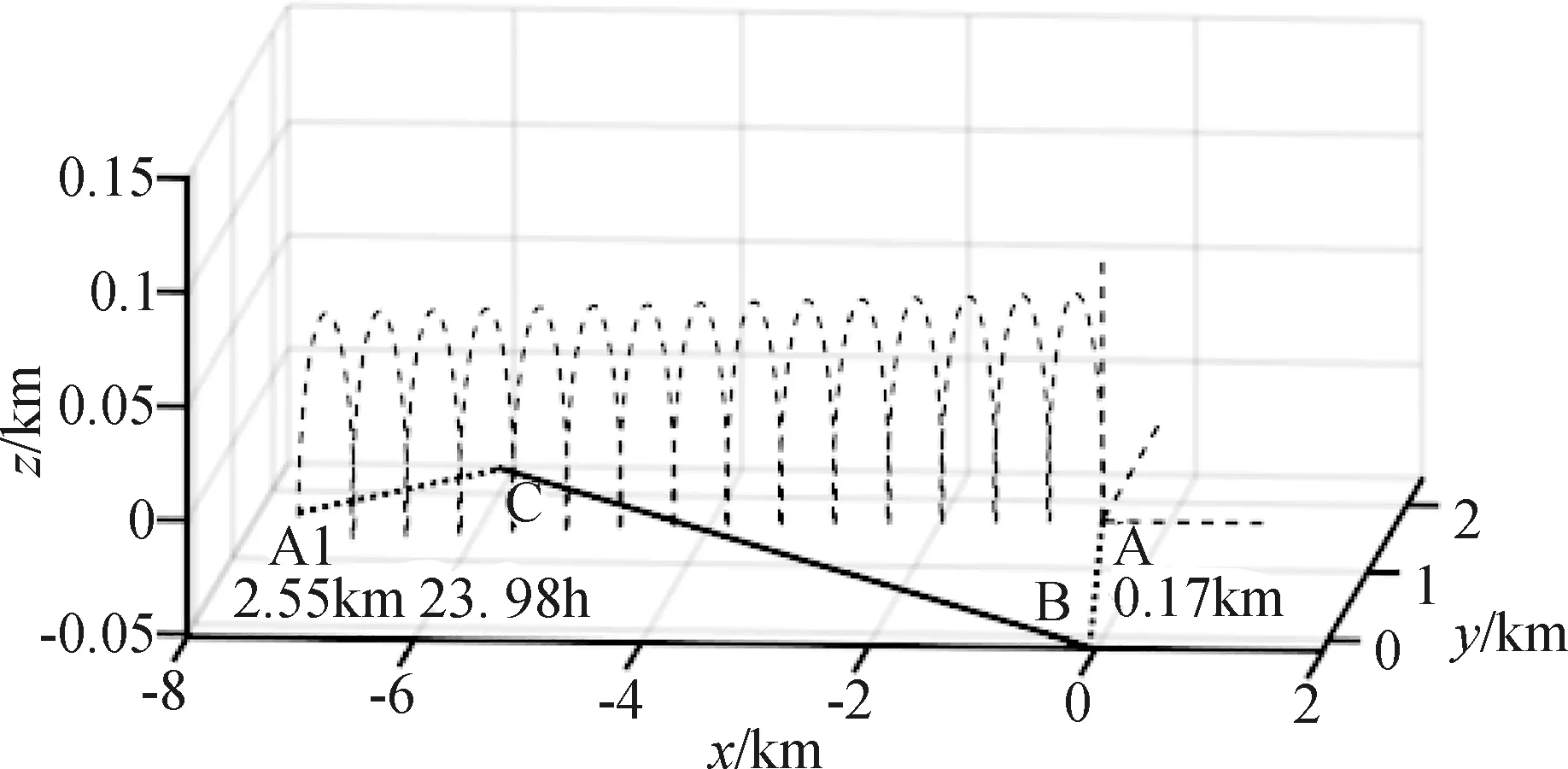
图1 接近场景示意图
首先,假设允许接近距离d0=2km。由式(13)和(14),用牛顿迭代法计算不同控制时刻对应的最小控制量的δa-t函数曲线(图2)。图2绘制了d0=1.8km、2km和2.2km三个允许接近距离对应的δa-t曲线。其次,假设允许的最小交垂线距离h0=100m,由式(18)计算不同控制时刻和控制量的函数曲线(图3)。图3绘制了h0=90m、100m和110m三个允许最小交垂线距离对应的δa-t曲线。可以看到曲线分为左右两支,同一控制时刻,对应正负2个控制量。
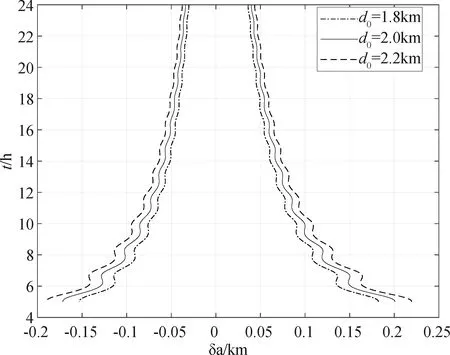
图2 最小接近距离约束δa-t曲线
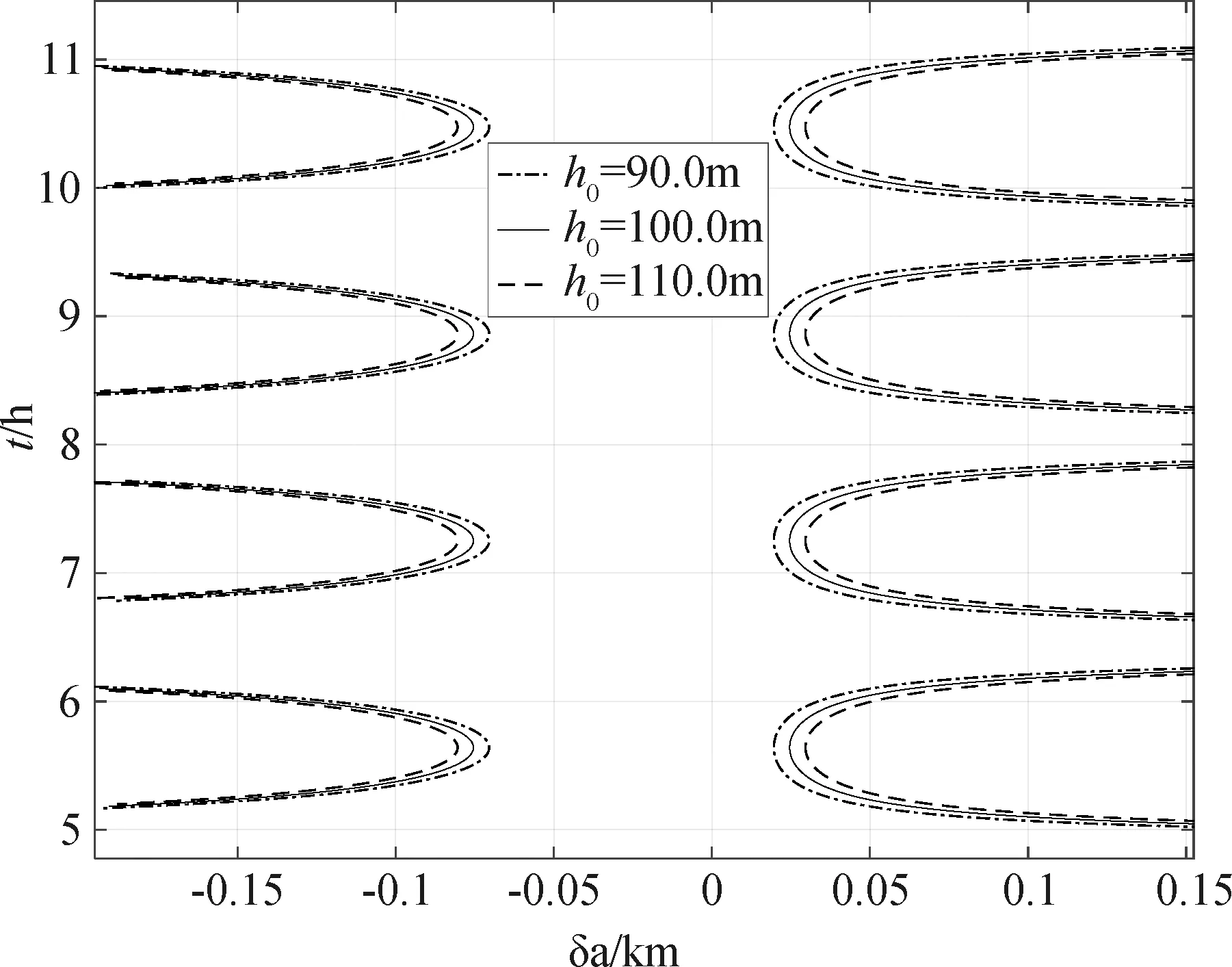
图3 最小交垂线距离约束δa-t曲线
为便于分析,将图2和3合并绘制如图4。图4中实线即表示每一控制时刻,分别由距离约束和交垂线约束确定的控制量中的较小值。据图4,可以确定满足规避约束条件的最小控制策略。首先确定控制时刻。考虑载荷应用、测控条件、卫星状况的诸多工程约束条件的限制,结合图4给出的δa-t曲线,确定控制时刻。其次确定控制时刻对应的最优控制量。半长轴机动方向受卫星推力器的安装位置和卫星姿控设计约束,为了节省燃料及尽量少偏离卫星工作轨道,半长轴控制量一般越小越好。图4中标出了A、a、B、b四个点,A、a纵坐标为交会前21小时的控制时刻,B、b纵坐标为交会前12小时的控制时刻。横坐标分别为对应时刻实施控制的最优控制量。在交会前21小时实施控制,会有A、a两个控制点,控制量分别为-39.3m和46.0m。从节省燃料和尽量少偏离卫星工作轨道的角度选择A点为最优控制点,即降低半长轴39.3m。如果因为卫星推力器设计不便于降低半长轴控制,可以采取抬高半长轴46.0m的策略;此时主要采取距离隔离的方式进行规避。在交会前12小时实施控制,会有B、b两个控制点,控制量分别为27.2m和-69.1m。从节省燃料和尽量少偏离卫星工作轨道的角度选择B点为最优控制点,即抬高半长轴27.2m;此时主要采取交垂线方向隔离的方式进行规避。将以上A、a、B、b四个点的控制策略采用高精度轨道控制及预报模型进行验证,满足距离隔离和交垂线隔离的要求,且是对应的最小控制量。
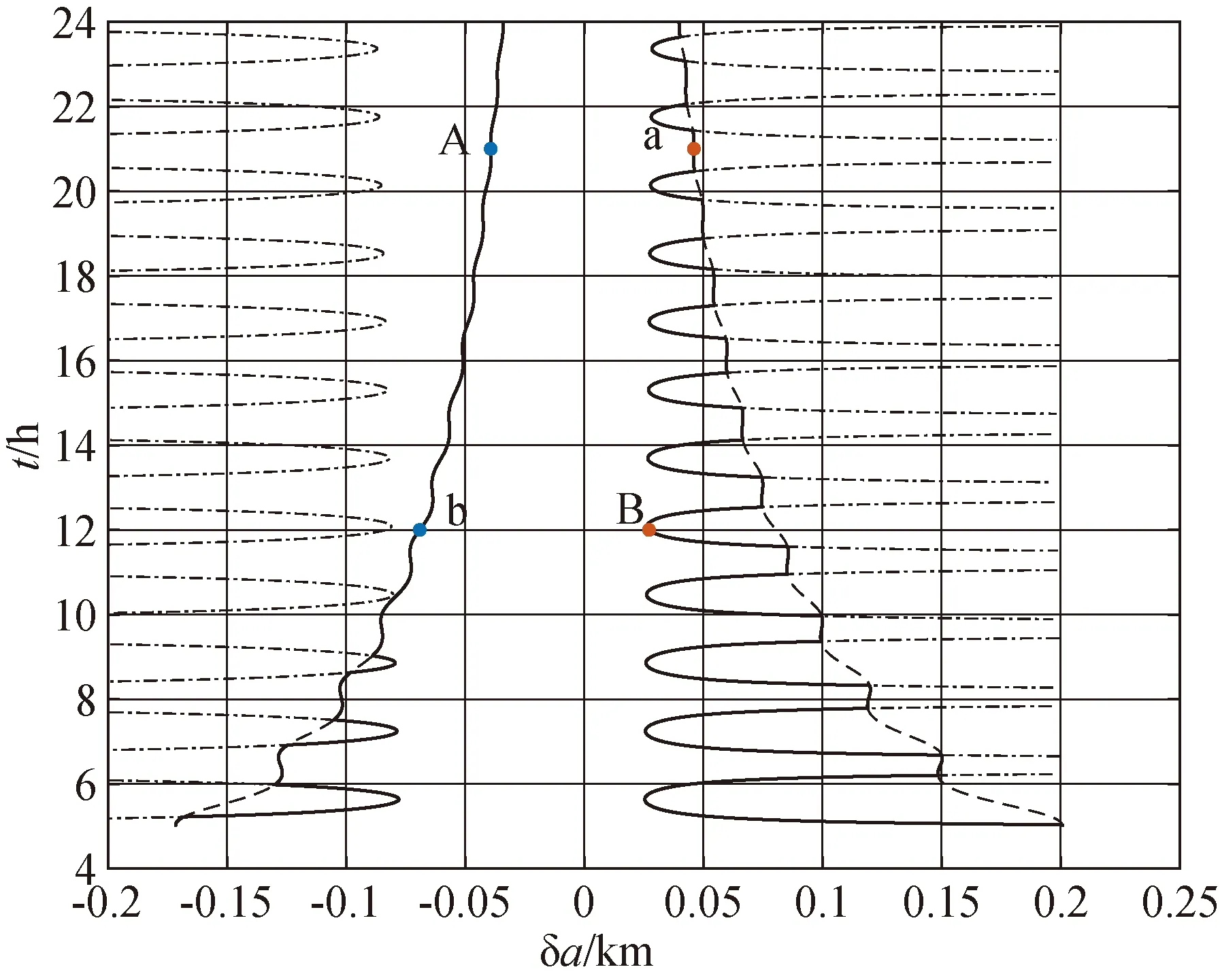
图4 接近安全约束下δa-t曲线
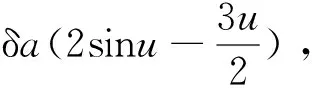
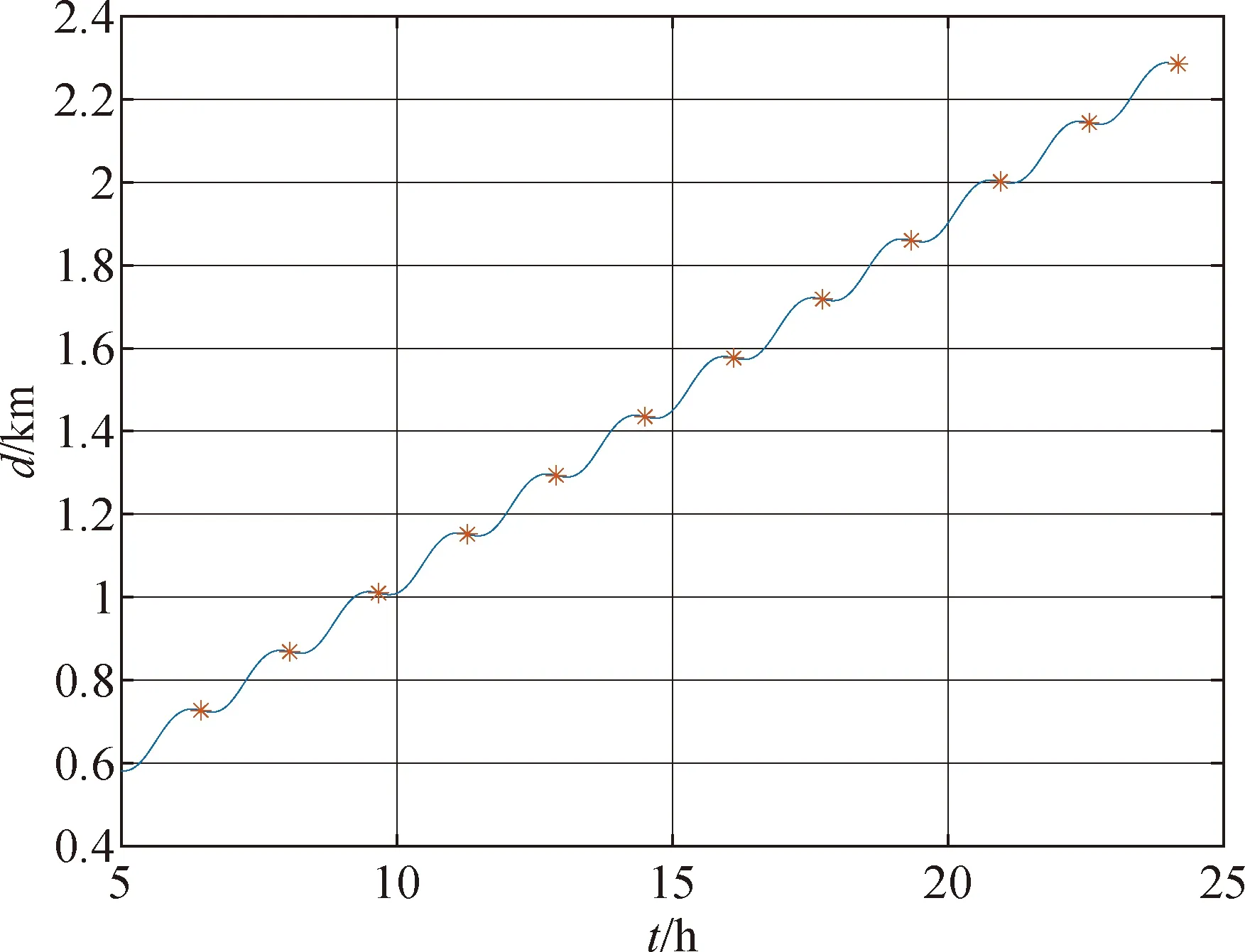
图5 控制时刻与接近距离函数曲线
对于交垂线隔离的情况,由式(18)可见,当相位差uk=(2k+1)π时,交垂线隔离距离需要的控制量最小。图4中B点确定的控制量为27.2m,在该控制量情况下,控制时刻与交垂线距离的关系如图6,图中星号表示的相位差是uk=(2k+1)π对应的控制时刻。
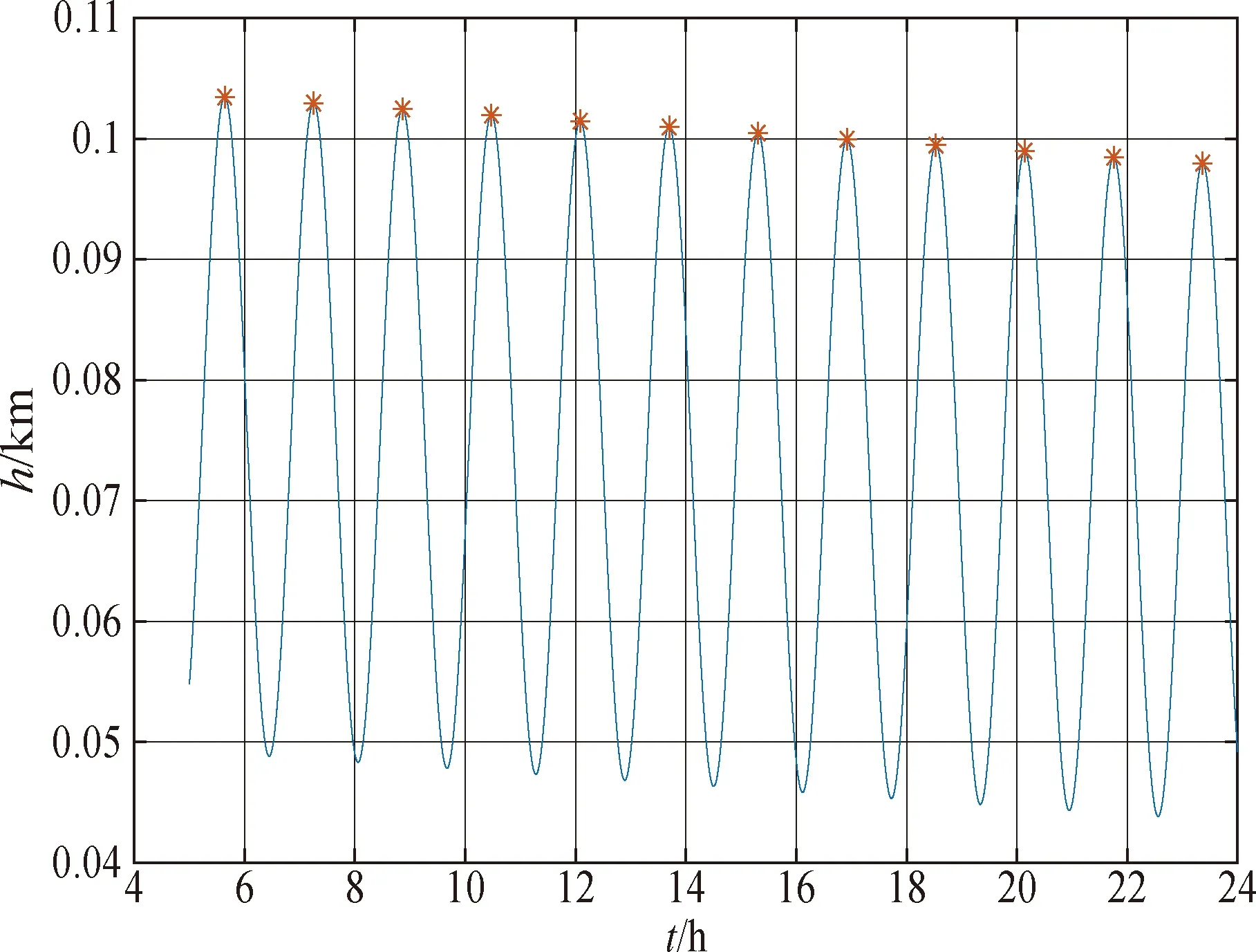
图6 控制时刻与交垂线距离函数曲线
4 结论
针对低轨航天器碰撞规避单脉冲切向最小控制量确定问题,采用相对轨道动力学理论方法,推导单脉冲切向控制情况下控后轨道与不控轨道的相对运动方程。定义了接近坐标系,在该坐标系中分析了碰撞预警交会点附近的相对几何关系,讨论了在最小接近距离约束、最小交垂线距离约束两种情况下,指定控制时刻对应的最小单脉冲切向规避控制量的确定方法,证明了控制量与规避距离的单调性关系。最后,通过算例给出了工程上可以应用的最小控制量确定流程,并讨论了控制时刻对控制效果的敏感性问题。分析表明,仅考虑对距离约束影响效果情况下选择控制时刻,在实施接近距离约束控制时,当控制点相位在交会点相位前后20分钟内,对接近距离的敏感性较小;当实施交垂线距离约束控制时,在距离交会点相位差180°位置控制,交垂线距离拉开效果最好;在控制时刻确定的情况下,前述两种距离约束确定的最小控制量是唯一的。大于该控制量的控制,均会使接近距离或者交垂线距离更大,满足预警解除的要求。以上单脉冲切向碰撞规避最小控制量的确定方法,可以适用于未来大数量在轨卫星对于日益增多的碰撞规避控制策略的需求,即仅需要交会点的空间接近信息和主星的空间速度信息,就可快速确定单脉冲切向规避最优控制量。
