复合干扰影响下战斗机大机动改进动态面控制*
2023-05-12李秋妮刘棕成张文倩
秦 川 陈 勇 李秋妮 刘棕成 张文倩
1. 空军工程大学,陕西 西安 710038 2. 中国人民解放军93793部队,北京 102100
0 引言
具备大机动能力的战斗机在现代空战中可以快速抢占有利位置、先敌开火,同时在遭到敌方武器锁定时能快速机动摆脱不利态势,从而显著提高战斗机的作战效能和生存能力[1]。战斗机在进行大机动飞行时,气动力和力矩呈现明显的非线性特性,三轴动力学严重耦合[2],同时阵风、紊流等外界扰动也会引起气动参数变化,导致飞机动力学模型存在较大的不确定性,给飞行控制系统设计带来巨大挑战。
反步法(Backstepping)作为非线性系统控制中常用的一种方法,在航空航天领域有着广泛的应用。文献[3]针对弹性吸气式高超声速飞行器控制问题,在反步法的框架下引入干扰观测器对复合干扰进行估计补偿,设计了一种鲁棒控制方案。文献[4]以反步法为基础,结合神经网络设计了高超声速飞行器的鲁棒自适应控制器。文献[5]将反步法与滑模控制相结合,为卫星姿态控制系统设计了容错控制器。文献[6-7]将反步法用于飞机的飞行控制器设计,取得了良好效果。然而,传统反步法需要对虚拟控制信号进行反复求导,导致控制律过于复杂,产生“微分爆炸”问题[8]。针对反步法的这一固有缺陷,文献[9]提出了动态面控制方法,通过引入一阶低通滤波器得到虚拟控制信号的一阶微分近似值,避免了对虚拟控制信号的直接求导,简化了控制律。动态面控制的核心是利用滤波器得到中间虚拟控制信号的一阶微分近似值,因此选择其他性能更优的滤波器代替一阶低通滤波器有助于改进动态面的控制效果。
神经网络对非线性函数具有良好的逼近能力,常用于处理系统中的不确定性,将动态面和神经网络结合,许多模型含有不确定性的飞行控制问题就能得到解决[10-14]。然而,用神经网络逼近未知函数需要清楚未知函数由哪些变量构成,当变量信息不足时,神经网络无法实现对函数的估计。由于实际飞行系统极其复杂,飞行器在飞行过程中所受干扰不确定,无法精确得知飞行器模型的不确定部分由哪些变量构成,因此神经网络方法存在一定的局限。此外,将模型不确定性作为复合干扰的一部分,基于干扰观测器进行控制器设计也是一种有效的方法[15-18]。但是,常规干扰观测器常需要假设干扰可导甚至慢时变[19-22]。这一假设在实际应用时过于严苛,因为实际被控系统很可能会受到死区、齿隙等不可导干扰的影响。而对于战斗机这样的对控制性能要求很高的复杂系统,考虑不可导干扰是很有必要的。文献[23]提出了一种新型干扰观测器,可有效处理不可导干扰,但是文中设计的干扰观测器结构复杂,需要调整的参数较多,不利于工程实现。
为此,本文针对含有不确定复合干扰的战斗机非线性模型,提出了一种改进动态面控制方案。利用改进的一阶滑模微分器估计虚拟控制信号的一阶微分,避免“微分爆炸”;同时基于文献[23]的思想提出了一种结构更简单的干扰观测器,对系统未知复合干扰进行估计和补偿;最后通过控制分配算法得到最终控制信号。将设计的控制器用于飞机大机动仿真以验证其有效性。
1 模型建立与问题描述
本文以某型战斗机六自由度非线性模型为研究对象,控制目标是实现对迎角、侧滑角和滚转角的跟踪控制,因此主要考虑姿态控制系统,数学模型如式(1)[6,10]。
(1)
式中:状态变量x=[φαβpqrθ]T分别表示滚转角、迎角、侧滑角、滚转角速度、俯仰角速度、偏航角速度和俯仰角,控制输入u=[δelδerδalδarδlefδtefδr]T分别表示左右升降舵、左右副翼、前后缘襟翼和方向舵7个相互独立的控制舵面,其余参变量含义与文献[10]相同。
定义x1=[φ,α,β]T,x2=[p,q,r]T,x3=θ则可将模型式(1)转换为如下形式[10]:
式中:y为系统输出;f1(x1,x3)、f2(x)、G1(x1,x3)和G2(x)为标称系统的向量或函数矩阵;d1(x,t)和d2(x,t)为复合干扰,d1(x,t)=Δf1+ΔG1x2+Δ1(t)、d2(x,t)=Δf2+ΔG2u+Δ2(t),式中Δf1、Δf2、ΔG1和ΔG2为系统未建模动态或飞机气动参数摄动引起的非线性不确定部分,Δ1(t)、Δ2(t)为外部干扰。


引理1[24]:对于一阶滑模微分估计器:
(3)
式中:φ1、φ2和ζ1为系统状态,h(·)为系统输入,选择合适的参数r1、r2和μ,则存在任意ϖ>0,使得以下不等式成立:
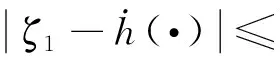
(4)
2 飞行控制器设计
2.1 控制律设计
控制律设计分为3步:1)设计虚拟控制律x2d;2)设计虚拟控制指令v;3)利用控制分配算法将虚拟控制指令v转换为实际控制指令u。为了得到虚拟控制律x2d的微分信号,基于动态面思想,本文采用式(3)所示的一阶滑模微分估计器对x2d的微分进行估计。一阶滑模微分估计器基于一阶滑模微分器[25]改进而来,利用双曲正切函数代替一阶滑模微分器中的符号函数,相比一阶低通滤波器具有更快的收敛速度并且克服了一阶滑模微分器输出不连续的问题。
首先定义跟踪误差变量:
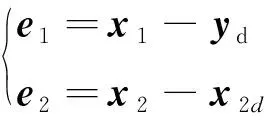
(5)
第1步:沿式(5)对e1求导得:
(6)
设计虚拟控制律x2d为:
(7)
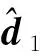
第2步:沿式(5)对e2求导,结合式(2)可得:
(8)
设计虚拟控制指令v:
(9)

第3步:控制分配
对于多操纵面飞机而言,虚拟控制指令v的维度小于操纵面的个数。为此采用控制分配技术实现虚拟控制指令v向多操纵面飞机各个舵面的指令分配。考虑操纵面偏转量的权值为优化指标,建立加权伪逆控制分配模型:
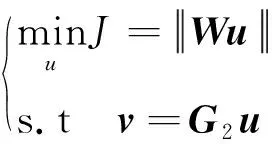
(10)
式中:W为正定对称权值矩阵,通过合理选择W可以协调各操纵面的偏转量,实现舵偏范围内的最优控制。根据最小二乘法,模型(10)的最优解为[26]:
(11)
2.2 干扰观测器设计
飞机模型(2)中的未知复合干扰项由气动参数摄动、未建模动态和外部干扰等多种因素引起。本文提出了一种结构简单,物理意义明确的干扰观测器来估计系统的未知复合干扰。
考虑如下系统:
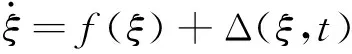
(12)
式中:Δ(ξ,t)为未知干扰,ξ为可测量的系统状态。
定义误差变量eξ=ξ-ξd,ξd为ξ的设计值,则有:
(13)
对上式整理可得:
(14)

(15)
根据上述分析,为获得d1和d2的估计值,构建如下干扰观测器:
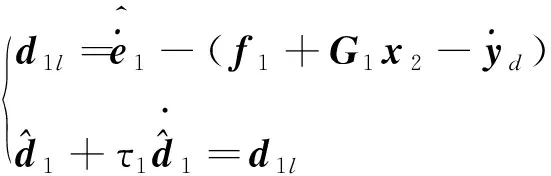
(16)
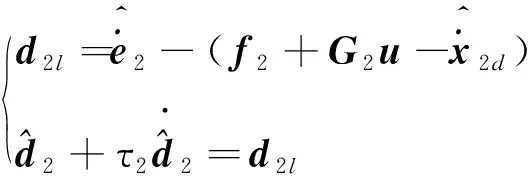
(17)
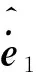
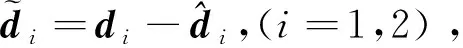
(18)
注1.之所以对d1l和d2l进行滤波,既为了得到较为平滑的控制信号,也为了避免出现“循环设计”。因为根据式(9)和(17)可以看出d2l和G20u相互耦合,利用一阶低通滤波器的延迟特性可以实现两者解耦。而将滤波器时间常数设置为递减的变化形式,可以加快滤波器初始阶段的收敛速度,并保证稳态误差不至于过大。
3 稳定性分析
定理1.考虑由式(2)表示的飞机数学模型,在满足假设1和2的条件下,设计基于干扰观测器式(16)和(17)构造的虚拟控制律式(7)和(9)以及基于控制分配算法构造的实际控制律式(11),通过选择适当的设计参数,能保证闭环系统半全局有界且使系统跟踪误差e1=x1-yd收敛到任意小。
证.定义Lyapunov函数:
(19)
将式(7)代入式(6),结合式(5)得:
(20)
将式(9)代入式(8)得:
(21)
对V求导得:
(22)
将式(20)和式(21)代入式(22)得:

(23)
由引理1结合Young不等式得:
(24)
由式(18)结合Young不等式得:
(25)
将式(24)和式(25)代入式(23)得:
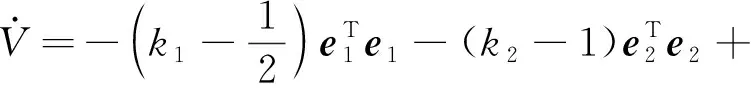
(26)
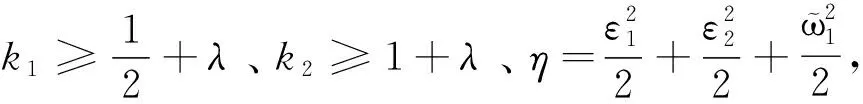
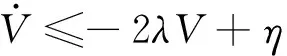
(27)
根据不变集原理[7-8],闭环系统所有信号半全局一致终结有界。
对式(27)两边积分得:
(28)
结合式(19)可得:
(29)
通过选择适当的一阶滑模微分估计器参数使η充分小,同时增大λ,则可使跟踪误差e1任意小。证毕。
4 大迎角机动仿真与分析
为验证本文方法的有效性,利用文献[27]中F-18战斗机相关气动参数取值进行仿真验证。初始条件为:高度h=914.4m,马赫数Ma=0.7,配平状态的迎角和俯仰角分别为α0=3.902°,θ0=3.902°。飞机各操纵舵面最大偏转角限定为±30°。假设飞机模型中气动参数存在0.3sin(0.5t)的变化量,即具有30%的周期性摄动。外部干扰设置为:

(30)
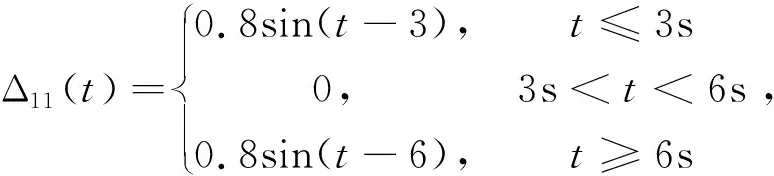
易知Δ11(t)、Δ12(t)和Δ13(t)是不可导的连续函数,所以复合干扰d1(x,t)是不可导的。
控制器参数选择为:k1=15、k2=15,所用到的一阶滑模微分估计器的参数均选择为:r1=20、r2=1、μ=0.1,干扰观测器参数选择为:p=0.1、w=1、q=0.2。采用两种方案对比仿真。
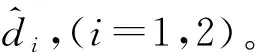
方案Ⅱ:引入本文设计的干扰观测器对复合干扰进行补偿。
由图1~3的姿态角(迎角、侧滑角、滚转角)响应曲线可以看出,在无扰观测器时,姿态角跟踪误差较大,而引入本文所设计的干扰观测器后姿态角能迅速跟踪参考信号,动态响应较好,跟踪精度明显提高,能够理想的完成飞机大机动动作。

图1 迎角响应曲线
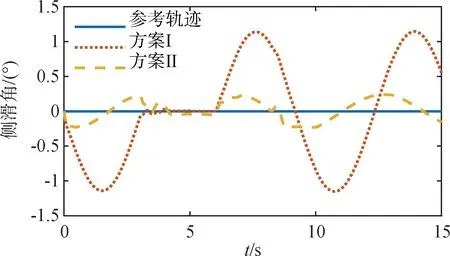
图2 侧滑角响应曲线
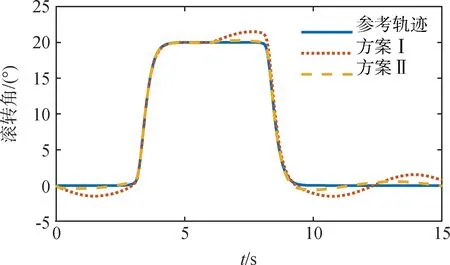
图3 滚转角响应曲线
5 结论
针对多操纵面战斗机飞行控制问题,考虑模型不确定性和外部干扰的影响,设计了基于干扰观测器的改进动态面控制方案。该方案能有效应对未知复合干扰,在气动参数具有较大不确定性和不可导外部干扰的情况下,所设计的控制器依然能够准确跟踪参考信号。控制器结构简单,易于实现,具有良好的鲁棒性。
