空间配试目标在轨释放与高精度轨道预报技术

谢文杰 唐启超 艾赛江 蔺博宇

中国人民解放军 63611部队,库尔勒 841001

0 引言

在航天装备研制和使用过程中,需要利用空间靶标配合完成试验鉴定、在役考核、跟瞄训练等任务。使用在轨工作卫星作为靶标,其目标特性和测量条件不能完全满足测试需求,既存在难以全面验证装备能力的问题,也存在损伤昂贵卫星的风险。航天装备试验和训练迫切需要各类经济性好、逼真度高的卫星替代物。空间配试目标(以下简称目标)是一种专门用于航天装备试验和训练的合作靶标,它采用卫星批量搭载方式进入预定轨道,受地面指令控制从卫星中释放,在空间展开成型后能够模拟典型空间目标的运动、光学、辐射、几何等特性,并与卫星协同配合完成试验训练任务的监视和测量。通过运用目标模拟真实太空环境,可以有效提高航天装备试验和训练的质量,加速航天装备的研制进程,同时在一定程度上降低试验训练活动的风险和成本。

从卫星上释放一个目标的变轨操作离不开轨道机动技术的支撑。根据动力的性质,轨道机动可分为脉冲推力、连续推力和连续小推力3种模型[1-3],大多数航天器都采用脉冲推力机动方式[2]。文献[4]实现了航天器空间悬停控制的多脉冲方法,解决了连续推力假设下对航天器控制推进系统要求较高、工程上实现困难的问题,提高了悬停精度。文献[5]利用基于摄动模型的非线性方程,规划脉冲变轨控制策略,实现了航天器高精度交会任务。文献[6]建立横向脉冲推力模型,得到与星下点轨迹有关的4个轨道要素和横向速度增量的关系,适于推力方向与卫星瞬时速度方向一致的机动应用。文献[7]根据航天器分离机构四根分离推杆作用机理,建立复杂的刚柔耦合动力学模型,为空间站、载人航天、探月工程等对分离姿态要求高的重大项目提供分析方法。从以上分析看,脉冲推力机动在理论和技术上比较成熟,可以满足多种空间任务需求。与上述应用场景不同,由于目标的质量远小于卫星,卫星只需提供很小的推力就能瞬间实现分离,并且对目标运动状态和轨道根数的改变很小。在小推力假设下,可以利用摄动模型研究脉冲式机动问题,并将复杂的非线性微分方程线性化,建立轨道六要素变化与速度增量的关系。

本文研究了目标在轨释放、初轨确定、高精度轨道预报问题,给出了相关的运动方程和数学模型,并利用某航天器仿真软件分析了目标释放分离规律和轨道衰减规律。本文对目标在轨释放过程的建模与星上分离机构的具体形式无关,分离后目标初始轨道确定计算过程简单,后续运动轨道预报能够满足工程应用精度要求。在航天任务中,目标在轨释放与轨道预报技术可为太空操控、态势感知、航天测控等装备进行任务规划和指挥控制提供支持。

1 目标在轨释放与初轨确定

空间配试目标随卫星一起在工作轨道运行,在适当时机由星上弹射装置提供推力,产生速度增量,使目标与卫星安全分离并进入目标轨道。要使地面能够精确控制目标在轨释放和确定目标轨道初始参数,必须建立速度增量Δv与轨道要素变化量Δσ之间的变化关系。

航天器瞬时运动特性可以用RTN(Radial-Track-Normal)轨道坐标系描述。该坐标系以航天器质心为原点,径向(R方向)由地心指向航天器质心方向,横向(T方向)在轨道面内与R正交,并指向航天器运动方向,法向(N方向)为轨道面法向,与R、T成右手系[8]。航天器轨道可以用经典轨道要素σ=(a,e,i,Ω,ω,M)描述,其中的分量分别为半长轴、偏心率、倾角、升交点赤经、近地点幅角和平近点角。

星上弹射装置对目标推力作用时间非常短,符合脉冲推力机动模式特征[2-3,9]。如果把推力也视为摄动,就可以用高斯型摄动运动方程来研究目标机动变轨[2-3]。由于小推力瞬间产生的速度增量较小,引起轨道要素微小的改变,所以可以将摄动运动方程线性化得到近似描述目标分离过程的数学模型[3,10]。

(1)

式中:ΔvR、ΔvT、ΔvN是RTN坐标系3个方向上的速度增量,a、e、i、Ω、ω、M为目标机动前轨道要素,Δa、Δe、Δi、ΔΩ、Δω、ΔM为冲量导致的轨道要素变化量。n为平运动角速度,f为真近点角,E为偏近点角,u为纬度幅角,这些轨道参数可以通过已知参数及换算关系获得,具体方法参考文献[3]和文献[11]。

已知原轨道和分离瞬时速度增量,根据如下关系可以计算出分离后目标初始轨道。反之,也可以由轨道根数的变化得到目标R、T、N方向上的速度变化,这样就可以由分离前后的轨道根数计算得出需要的速度增量。

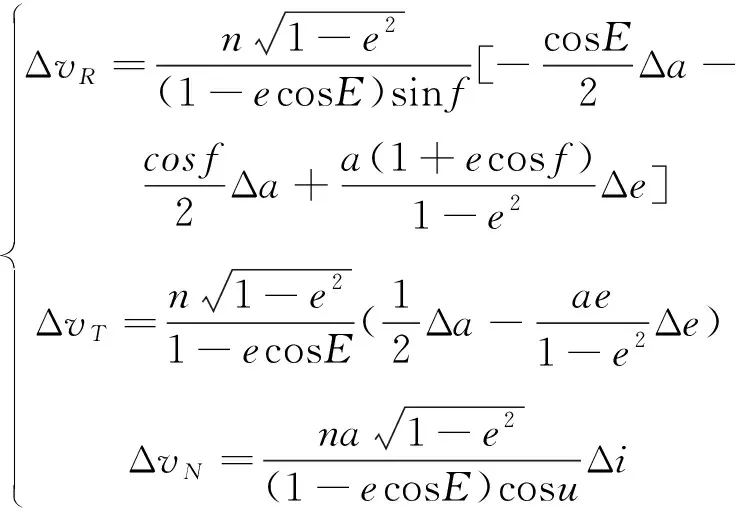
(2)

在式(1)和(2)中,包含e、sin(i)的项出现在某些方程的分母上,当e=0和i=0时计算会引起数值问题。对于近圆轨道,近地点定义本身不完备[11],轨道的微小变化会引起近地点位置的较大改变,在求解E时会有奇异。上述现象是由经典轨道要素定义的奇异性引起的[3,11],可以选择一组无奇点轨道要素来避免奇异现象。采用春分点轨道要素[3,11]建立的摄动运动方程如下:

(3)

式中:a、h、k、p、q和λ为春风点轨道要素,Δa、Δh、Δk、Δp、Δq和Δλ为春分点轨道要素变化量,r为航天器到地心的距离。真经度L=f+ω+Ω,偏经度F=E+ω+Ω,春分点要素的定义如下[3,11]

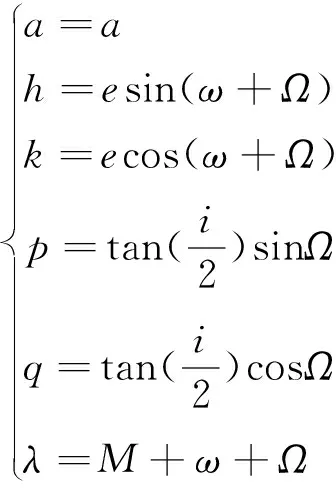
(4)

根据式(3)和(4)可以推导出反向计算速度增量和经典轨道要素的公式,这里不再列出。经典轨道要素能够直观地表示轨道大小、形状、方位特性,并且比春分点轨道要素表示的公式形式简单,所以用式(1)和(2)分析速度增量对轨道的影响更加方便。

2 目标高精度轨道预报

空间配试目标从卫星上分离出来以后开始做无动力自由飞行,即进入受摄开普勒运动阶段。目标上一般未安装测控通信载荷,为保障测控系统跟踪测量和航天装备试验训练任务规划,需要对目标进行高精度轨道预报。解决航天器运动问题,首先要建立符合实际的航天器动力学方程。在牛顿物理框架下,考虑轨道摄动时航天器运动的微分方程可以表示为

(5)

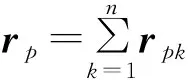
2.1 地球的引力势

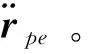
(6)

(7)

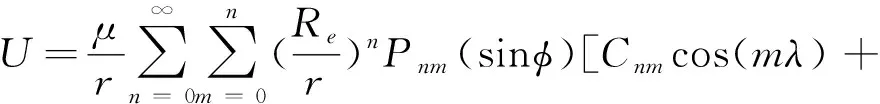
Snmsin(mλ)]

(8)

式中:Re为地球的赤道半径,λ和φ为经度和地心纬度,Pnm为n阶m次缔合勒让德多项式,球谐系数Cnm和Snm描述了地球内部质量分布关系,具体定义参考文献[11]。由于地球内部质量分布未知,球谐系数不能直接计算得到,使用卫星跟踪、陆基重力计以及高度计测量来间接确定地球引力场,一组球谐系数往往称为一种引力场模型。目前建立了一系列不同复杂度的引力场模型,如戈达德地球模型(Goddard Earth Model,GEM)、联合重力场模型(Joint Gravity Model,JGM)、EGM96(Earth Gravity Model 96)地球重力场模型等。

2.2 大气阻力摄动

大气阻力是作用在低轨航天器上的最大的非引力摄动[8,11],方向与航天器相对于气流运动速度方向相反,其产生的航天器加速度计算公式为

(9)

式中:CD为无量纲阻尼系数,在距离地面180km以上的大气中可以看作常数,取值在2.2附近[3,8]。m为航天器的质量,将A/m称为航天器的面质比,vr是航天器相对于大气的速度,单位矢量ev=vr/|vr|。ρ是航天器所在位置的大气密度。航天器轨道确定和预报需要使用复杂的大气模型,常用的有Harris-Priester密度模型、Jacchia 1971密度模型、Jacchia-Roberts密度模型等[11]。

2.3 第三体引力摄动

第三体引力摄动主要考虑太阳和月亮的作用,并且把第三体作为质点。航天器在地心惯性坐标系下的第三体引力摄动加速度为

(10)

式中:r、st分别为航天器和天体的地心位置矢量,Mt为天体的质量。

2.4 太阳光压摄动

在太阳光照射下的航天器会受到光子吸收或者反射所产生的微小力的作用。太阳光压引起的加速度依赖于航天器的质量和表面积,其大小为

2εcos(θ)n]

(11)

式中:1AU表示日地平均距离,Ps为太阳光压常数,rs为太阳地心位置矢量,A是航天器吸收或反射光子的有效横截面积,θ为太阳光子入射方向与有效横截面法向单位矢量n的夹角,es为指向太阳方向的单位矢量,ε为航天器表面材料反射系数,CR=1+ε为光压系数。太阳光压对面质比大于2.5m2/kg的航天器影响尤为明显[3]。

以上列出4种主要摄动加速度的解析表达式,可以用数值积分方法求解式(5),得到航天器在任意时刻的位置和速度。对微分方程有龙格-库塔法、多步法、外插法等多种数值积分方法,其中龙格-库塔法适用范围广,用法简单。实际应用表明,只有高阶龙格-库塔类方法才可以满足轨道计算精度要求,而RKF7(Runge Kutta Fehlberg 7)是Fehlberg给出的7阶著名方法[11]。在航天器轨道预报中,总的计算时间主要取决于实际动力学模型,积分开销反而可以忽略[11]。对于地球引力场、大气密度需要合理确定模型复杂程度,以降低计算量和系数存储需求。

3 仿真分析

使用某航天器仿真软件对空间配试目标在轨释放和自由飞行轨道进行仿真和分析。在仿真场景中模拟1颗太阳同步轨道卫星S,初始轨道根数σS0=(6991.137km,0,97.748°,234.005°,0°,0.07°)T,卫星具有轨道保持能力,所以假定其运动符合二体运动模型。星上搭载3个轻质目标T1、T2和T3,它们展开后的面质比分别为0.5m2/kg、1.5m2/kg和3.0m2/kg。利用软件轨道机动功能模块中的跟随(Follow)、轨道机动(Maneuver)、轨道外推(Propagate)组件实现目标在轨释放前后各个飞行阶段的轨道仿真[12]。仿真开始时间为2021年7月1日0时(UTC),结束时间为2022年7月1日0时(UTC),仿真软件轨道机动功能模块的主要模型参数见表1。

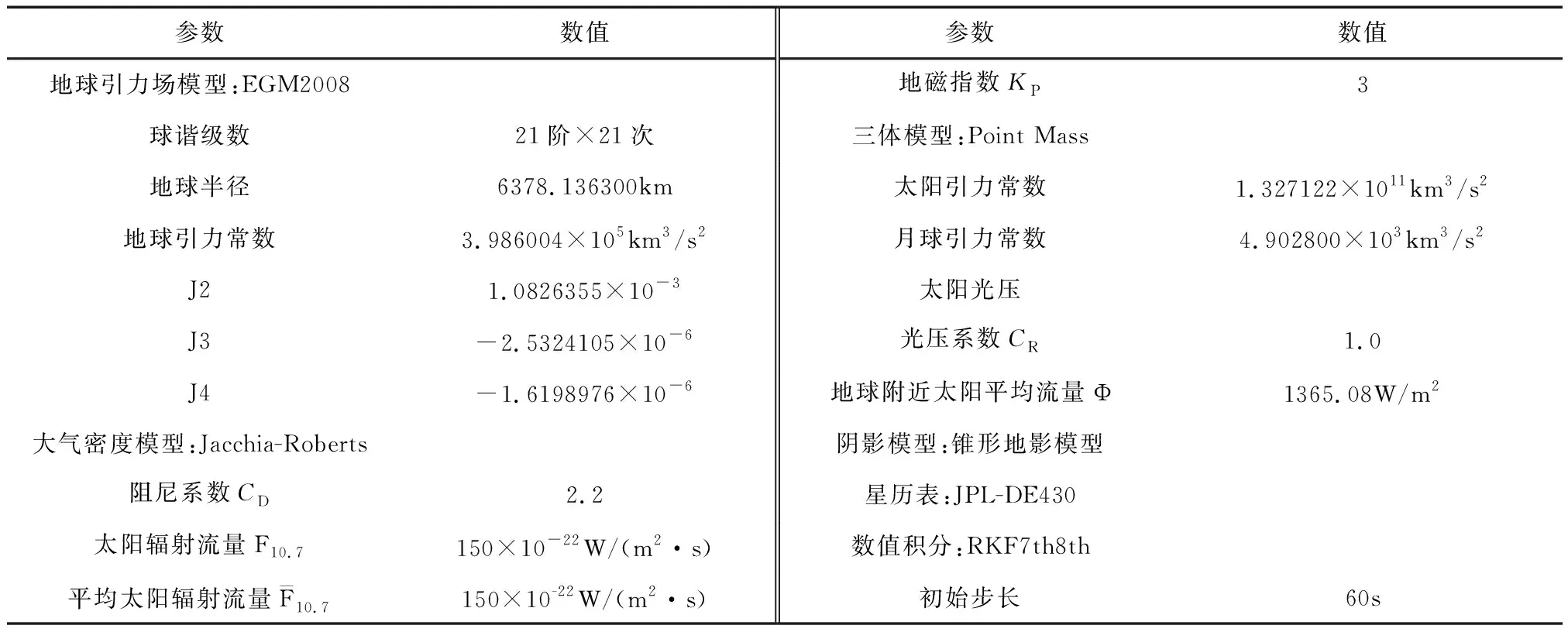
表1 软件轨道机动功能模块模型参数

T1、T2和T3首先与S一起在轨运行,在2021年7月3日8时(UTC)与S分离。使用脉冲机动模型模拟目标在轨释放,在分离点沿目标运动方向施加一个速度增量Δv1=(0m/s,0.5m/s,0m/s),从而使目标安全脱离卫星进入预定目标轨道。某航天器仿真软件计算的轨道要素变化量为Δσ1=(926.029000m,0.000132,0.000000°,0.000000°,235.638000°,128.075000°),根据式(3)和(4)计算的结果为Δσ2=(925.876010m,0.000132,0.000000°,0.000000°,231.925000°,128.136883°)。反之,由仿真工具软件确定的目标分离前后轨道,根据式(3)和(4)反向计算得到速度变化量为Δv2=(-0.064546m/s,0.500083m/s,0.000000m/s)。可见,Δv1与Δv2、Δσ1与Δσ2之间的误差较小,分离后目标轨道初始值相对误差不大于1.576%,说明上述公式描述的脉冲机动速度增量与轨道要素变化的关系是正确的。

目标与卫星分离之后开始进入无控飞行阶段。根据软件确定的目标初始轨道,使用轨道预报功能计算每一时刻目标的瞬时轨道根数,直到距离地面200km高度停止外推。图1～2是T1、T2和T3的轨道半长轴a1、a2和a3随时间变化曲线。从图1可以看到,在各种摄动力的作用下,引起目标轨道半长轴周期性变化,一个轨道周期内在波峰波谷之间转换4次,最大振荡幅度约20km。图2反映了大气阻力导致目标轨道高度不断下降,目标面质比越大,轨道高度下降的速度越快。T1、T2和T3保持轨道高度550km(半长轴约6928km)以上时间分别为84d、32d和16d,平均每天轨道高度衰减分别为0.908km、2.384km和4.716km。

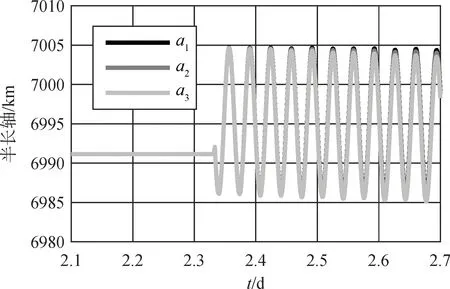
图1 摄动力对目标轨道的影响

目标与卫星分离之后,相互之间可视距离随时间变化关系如图3～4所示。历时约11.5个卫星轨道周期(1116.432min)后,目标与卫星分开的距离就达到1000km,并且在目标生命周期的绝大部分时间相距遥远,仅在地球两极上方因轨道交叉而短暂靠近。可见满足卫星对目标观测距离条件的时间很少,除了在轨分离之后的极短时间,卫星必须具备强大的机动能力才能主动接近目标,以利于观测空间试验任务状况。

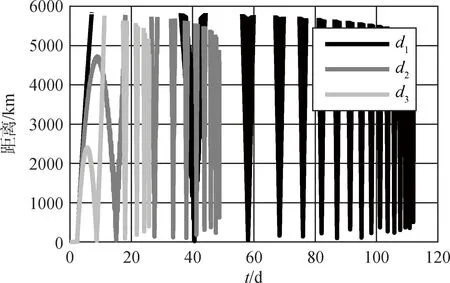
图3 目标相对卫星可视距离的变化

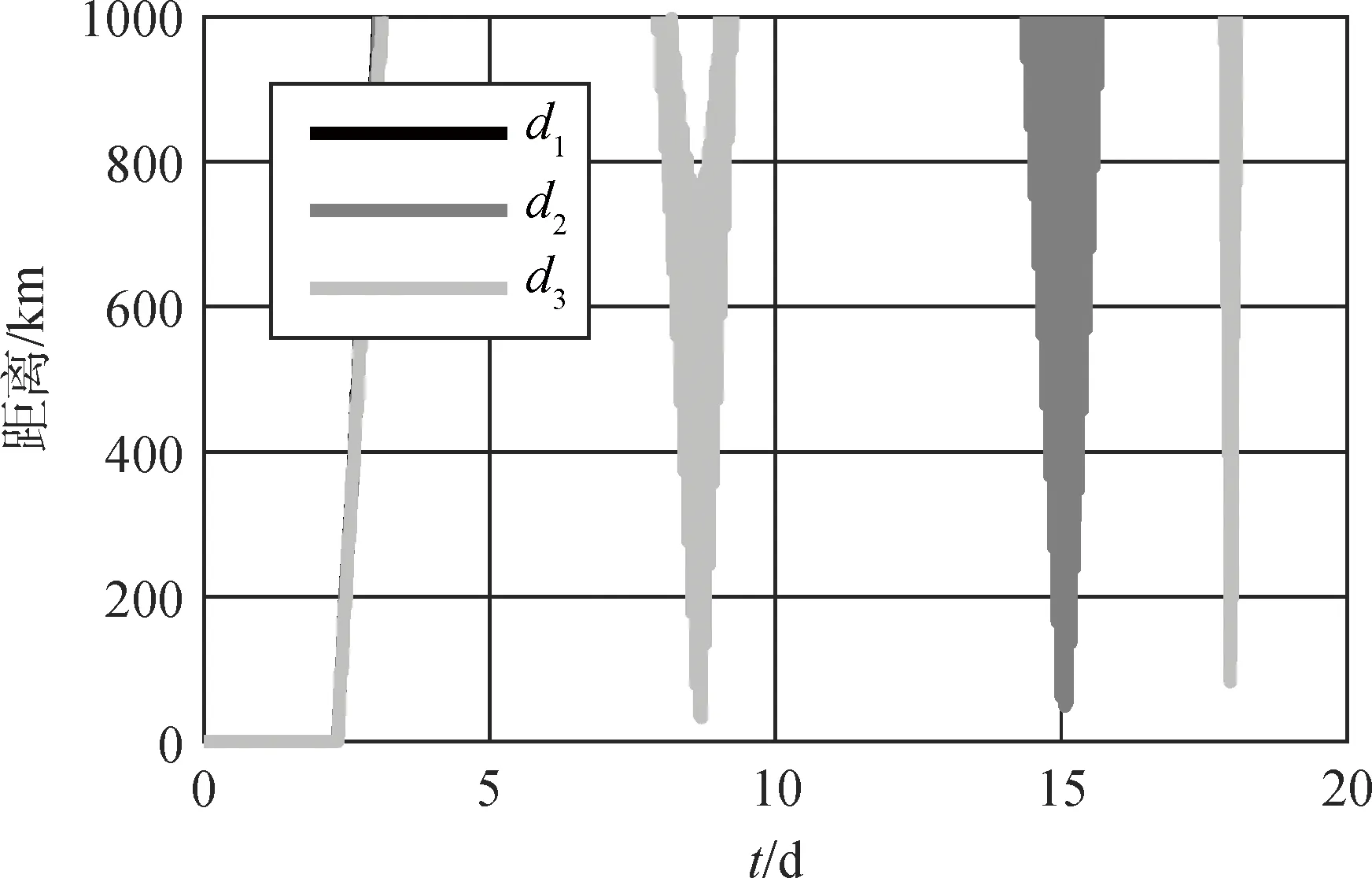
图4 目标相对卫星可视距离变化的局部放大

4 结束语

空间配试目标是开展航天装备试验和训练的重要资源,可以达到大型试验结果可测、风险可控,效费比提高等目的。本文给出了目标在轨释放、初轨确定和高精度轨道预报方法,并利用某航天器仿真软件进行计算,经结果分析得到以下结论:1)目标轨道高度衰减很快,不会长期在轨影响空间环境;2)不同面质比的目标维持一定高度轨道的能力不同,对空间任务规划有重要影响;3)目标与卫星可视距离一般较远,卫星需要较强的机动变轨功能才能实现对目标的监控。此外,目标在轨分离前后是执行空间任务难得的有利时机,后续考虑测控、通信、光照等约束条件,计算确定最佳分离点的位置和时刻。