一种离子型稀土矿体渗透性空间分布的计算方法

王明照 ， 龙平， 胡世丽 ， 王观石 ， 罗嗣海， 洪本根*,2

（1. 江西理工大学土木与测绘工程学院，江西 赣州 341000； 2. 龙岩市稀土开发有限公司，福建 龙岩 361000）

0 引 言

中重稀土是国防军工装备和高精尖产品不可缺少的元素[1-3]，离子型稀土矿床是其主要资源类型。 现阶段离子型稀土矿床主要采用原地浸矿工艺进行开采，以硫酸铵、硫酸镁等电解质做浸矿剂[4-6]。 大量实践研究证实[7-9]，渗透系数对浸矿剂的消耗和稀土的浸取效率有重要影响。 通常，渗透系数越大，浸矿剂消耗越少，稀土的浸取效率也越高[10-11]。 因受到不同成矿地质条件及环境因素等影响， 渗透系数常常具有明显的空间变异性，因而，合理确定稀土矿体渗透系数的空间分布， 成为精准开采离子型稀土矿床的重要前提[12]。

确定矿体渗透系数空间分布的方法主要有2 类：①原位测试渗透系数。 如，文杰等[13]将瞬间剖面法推广至原位渗透系数的测试， 较好地确定了4 m 深度范围内矿体的渗透系数；林鸿州等[14]则采用双环法测试了原位黄土的渗透系数。这2 种方法均适用于表土渗透系数的测试，而离子型稀土矿埋深和矿层的厚度大多在10 m 以上，因而难以用于大埋深矿体渗透系数的确定。②现场取样和室内测试渗透系数。这类方法通过建立矿土易测的物理力学参数与渗透系数的关系，进而间接计算出试样的渗透系数。如，赵茜等[15]通过矿土级配研究，查明了渗透系数各向异性的变化规律；许多学者建立了级配、孔隙比与渗透系数的关系[16-17]，仅需现场取样，结合室内测试级配和渗透系数即可估算原位渗透系数及其分布；张昭等[18]还从理论层面提出了孔隙半径的计算方法，并基于泊肃叶公式提出了非饱和渗透系数函数的预测方法；刘一飞等[19]提出一个包含级配参数的渗透系数计算公式。然而，离子型稀土矿床因其较为特殊的地质产出特性， 虽然砂粒含量较多，但富含结构差异性极大的黏粒，颗粒级配连续性较差，如龙南等矿床最具代表性[20]。 因而直接采用现有的渗透系数确定均会出现较大误差， 导致其代表性差而难以有效指导矿床的精细化开采。

本文通过室内试验研究颗粒级配和孔隙比对离子型稀土矿土渗透系数的影响规律，建立根据级配和孔隙比计算渗透系数的数学模型，并经与试验数据对比验证其合理性，结合普通克里金法，建立一种离子型稀土矿体渗透系数空间分布的计算方法，为精准开采离子型稀土矿床提供重要参数。

1 试验方法

1.1 矿土级配

试验用矿土取自福建省某离子型稀土矿床。矿土中的粗粒采用GZS-1 型高频振筛机 （浙江德东电机股份有限公司）测试级配，筛网孔径从上到下依次为2、1、0.5、0.25、0.1、0.075 mm， 小于 0.075 mm 的细粒采用BT-2022 型激光粒度仪 （丹东百特仪器有限公司）测试级配（加入偏磷酸钠作为分散剂）。 经统计分析，获得矿土的粒径累积曲线图（见图1）。

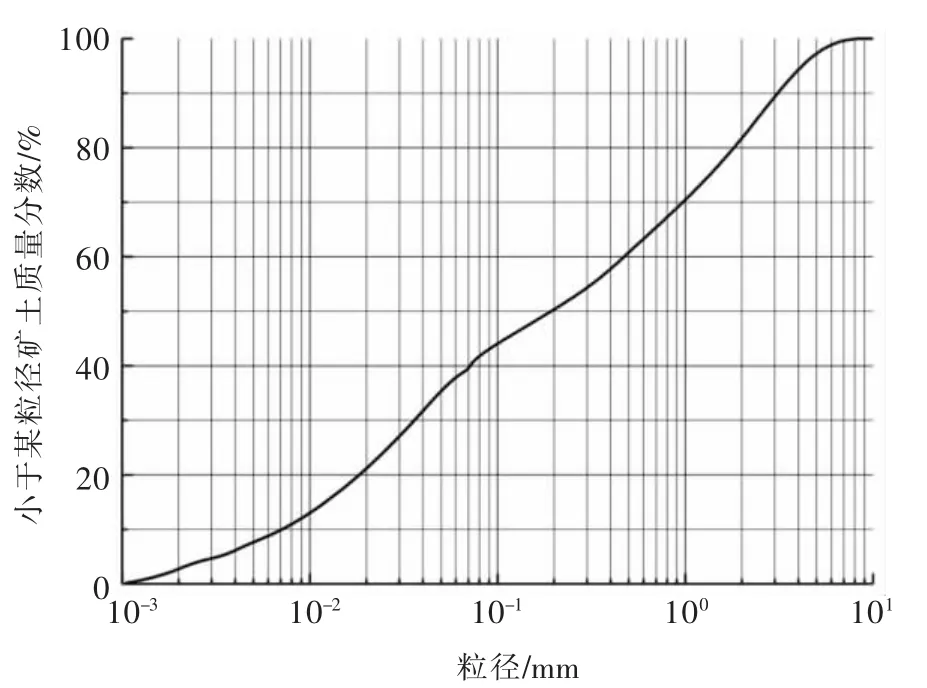
图1 矿土的粒径累计曲线Fig. 1 Cumulative curve of particle size of mine soil

1.2 渗透系数测试试验

用 《土工试验方法标准》（GB/T 50123—2019）[21]提出的变水头试验测试矿土的渗透系数；设置含水率为10%（质量分数），往矿土中加水湿润，充分搅拌并静置一天后，用直径6.16 cm、高度4.00 cm 的环刀，按干密度分别为 1.35、1.40、1.45、1.50、1.55、1.60 g/cm3装入矿土， 对应的孔隙比依次为 1.00、0.93、0.87、0.80、0.75、0.69，将装好矿土的环刀装入TST-55 型渗透仪（南京土壤仪器有限公司生产）中。

为了分析级配对渗透系数的影响，对部分矿土样品进行筛分，筛网的孔径为0.075 mm，将原矿土与小于0.075 mm 的矿土进行不同比例的混合，以此配置不同级配的矿土，矿土按如表1 所列比例混合，依次用S0—S6表示。 采用变水头试验确定不同级配矿土的渗透系数。

表1 矿土的混合比例Table 1 Mixed proportion of mine soil

1.3 矿体的颗粒级配测试

在上述试验矿体布置13 个取样孔，依次编号为1#—13#，取样孔位置如图2 所示，每个取样孔每隔1 m取一个样，每个样约1.0 kg，取样深度直至洛阳铲无法继续往下打为止。对每个矿土样放入温度为105 ℃的烘箱中烘10 h，待冷却后，先采用高频振筛机对矿土进行筛分 （筛网孔径从上至下依次为 2、1、0.5、0.25、0.1、0.075 mm），对小于 0.075 mm 的矿土采用偏磷酸钠溶液分散后， 通过激光粒度仪测试级配，即可得到各个取样点的矿土的粒径累计曲线。 去除取样孔附近的0.5 m 的表土， 采用环刀法测试矿土的孔隙比。

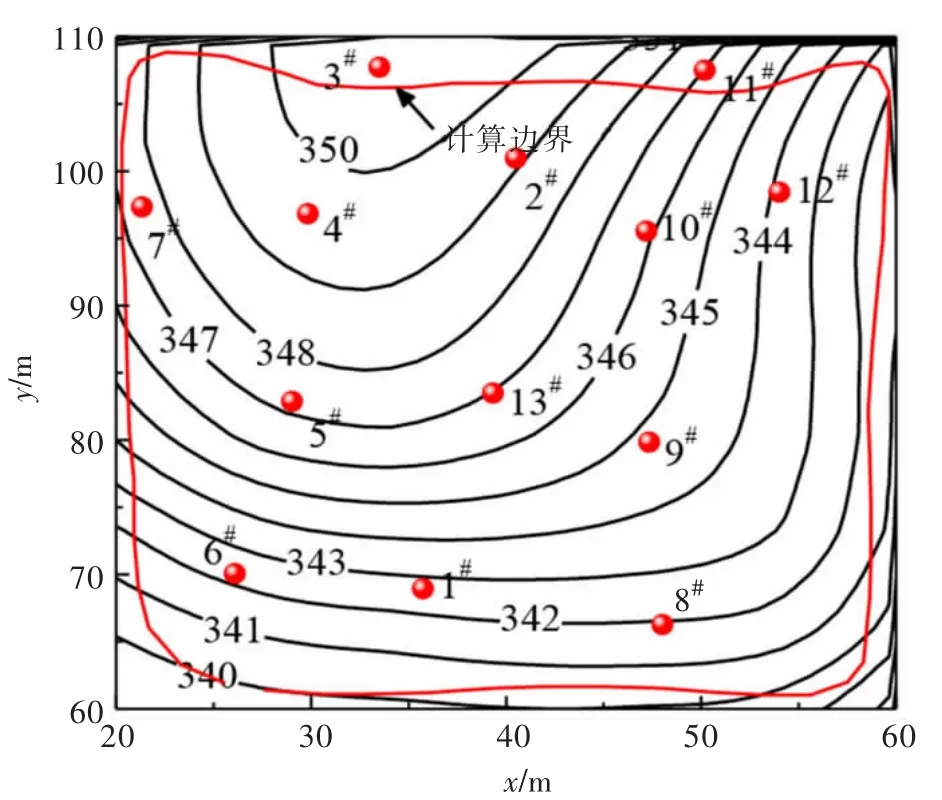
图2 取样点位置Fig. 2 Location of sampling points

2 结果分析

2.1 矿土的分类

根据图1 所示的粒径累积曲线，可以得到试验矿土中巨粒（d＞60 mm）、粗粒（0.075 mm＜d≤60 mm）和细粒（d≤0.075 mm）的占比分别为36.79%、21.37%和 41.84%，其中粉粒（0.005 mm＜d≤0.075 mm）和黏粒（d≤0.005 mm）占细粒组的比重分别为81.19%和18.81%，根据《土的工程分类标准》（GB/T 50145—2007）[22]，本次研究的矿土为粉土质砂类土。 根据图1，可以计算出 d10、d30和 d60（d10、d30和 d60分别为小于某粒径土重累积百分数为10%、30%和60%） 分别为0.007、0.036、0.475 mm，不均匀系数 Cu（Cu=d60/d10）和曲率系数 Cc（Cc=d302/d10/d60） 分别为 66.63 和 0.385，Cu≥5，Cc＜1，表明本次研究矿土的粒度级配不良。

2.2 渗透系数与 e、d10 和 Cu 的关系

影响粉土质砂渗透系数的主要因素为d10、 不均匀系数（Cu）和孔隙比（e）[23]，根据图 1 和表 1，可以得到 S0—S6矿土的 d10、d60和 Cu，结果见表 2 所列。

表2 矿土的 d10、d60 和 Cu 的计算结果Table 2 Calculation results of d10、d60 and Cu in mine soil

由前述渗透系数试验， 可得到渗透系数随e、d10和 Cu变化的测试结果， 分别如图 3、 图 4 和图 5 所示。 由图 3—图 5 可知，lgk 与 e、d10和Cu均具有良好的线性关系。 分别采用线性函数 lgk-e、lgk-d10和lgk-Cu的数学关系进行量化计算， 其关系分别为式（1）—式（3）：

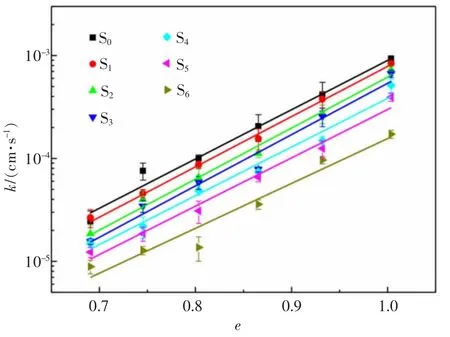
图3 渗透系数（k）随孔隙比（e）的变化情况Fig. 3 Variation of permeability coefficient （k）with void ratio （e）

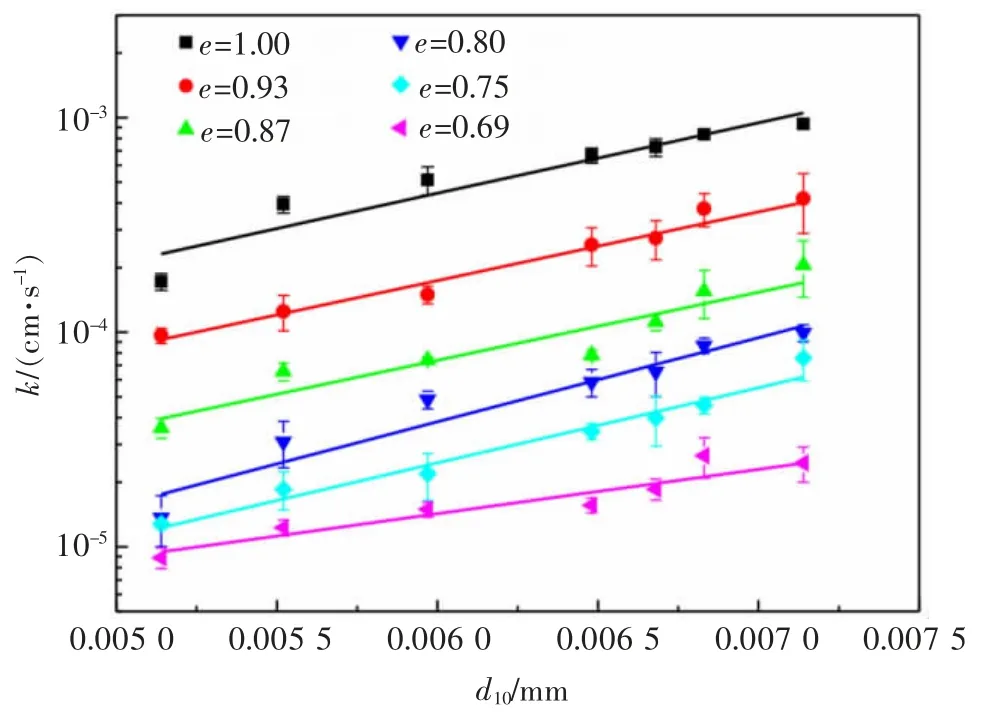
图4 渗透系数（k）随d10 的变化情况Fig. 4 Variation of permeability coefficient（k）with d10

图5 渗透系数（k）随Cu 的变化情况Fig. 5 Variation of permeability coefficient （k） with Cu

式（1）—式（3）中：k 为渗透系数；e 为孔隙比；d10和 d60分别为小于某粒径土重累计百分数为10%和60%对应的粒径 ；Cu=d60/d10；a1、a2和 a3为斜率；b1、b2和 b3为截距。

采用式（1）—式（3）分别拟合图 1—图 3 的试验数据，拟合结果列于表3。 结果显示，对于lgk-e 数据和lgk-d10数据， 采用线性函数拟合的决定系数均大于0.830；而对于lgk-Cu数据，拟合效果稍差，但决定系数均在0.750 以上。 由此可见，可以采用线性函数分别描述 lgk 与 e、d10和 Cu的关系。

表3 拟合结果Table 3 Fitting results

图3—图5 中拟合直线斜率的均值（μ）和标准差（σ）结果列于表 3。 同时，根据 Cv=σ/μ 确定变异系数Cv，k-e 结果的变异系数为 4.4%， 远小于 20.00%，说明d10和Cu对k-e 直线的斜率影响较小。 k-e 结果和k-Cu结果的变异系数分别为19.4%和19.6%，均小于20.0%。 这说明，孔隙比对k-d10直线斜率与k-Cu直线斜率的影响均较小。 总体上看，可以将e、d10和Cu对渗透系数k 的影响视为线性相关，因而e、d10和Cu与k 的关系可以采用式（4）描述：

式（4）中：b 为待定常数。

3 粉土质砂类土渗透系数的估算方法

3.1 估算方法

以 a1、a2、a3和 b 作为基本未知量， 利用式（4）拟合图3—图5 的数据，得到各个参数的结果分别为：a1=5.16，a2=240.97，a3=9.72×10-3，b=-10.51，将其代入式（4），即可得到 e、d10和 Cu与 k 的数学关系为：

采用式（5）计算得到的不同 e、d10和 Cu对应的渗透系数，结果如图6 所示。 常用干砂土渗透系数估算的 Amer 模型（式（6））[16]的计算结果见图 6。

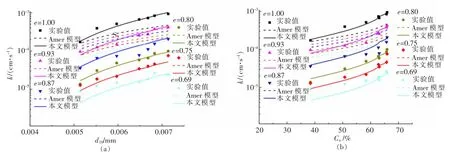
图6 渗透系数计算结果的对比Fig. 6 Comparison of calculation results of permeability coefficient

式（6）中：C2为常数，以 C2为基本未知数，采用式（5）拟合图 6 的实验值确定 C2为 6.36×10-4。

分别采用式（7）和式（8）计算决定系数和平局相对误差，以量化评价计算误差。

式（7）—式（8）中：i 为实验数据的编号，i=1，2，3，…，I， I 为总实验点数；ki和分别为渗透系数的实验值和估算值；为渗透系数实验值的平均值；R2为决定系数；δ 为平均相对误差。

经计算， 本文提出方法和AMER 模型计算的决定系数分别为0.986 和0.707， 平均相对误差分别为15.1%和260.7%。 可见，本文提出方法的精度明显优于Amer 模型，估算离子型稀土矿（土）渗透系数的精度较高。

3.2 渗透系数的空间分布估算及合理性分析

采用环刀法测试得到1#—13#取样孔的孔隙比e依 次 为 0.84、0.86、0.86、0.84、0.80、0.79、0.80、0.80、0.75、0.77、0.81、0.76、0.82，每个取样点的 d10和 Cu值如图 7 所示。把 e、Cu和 d10值代入式（5），即可得到每个取样点处稀土矿（土）的渗透系数（图8）。

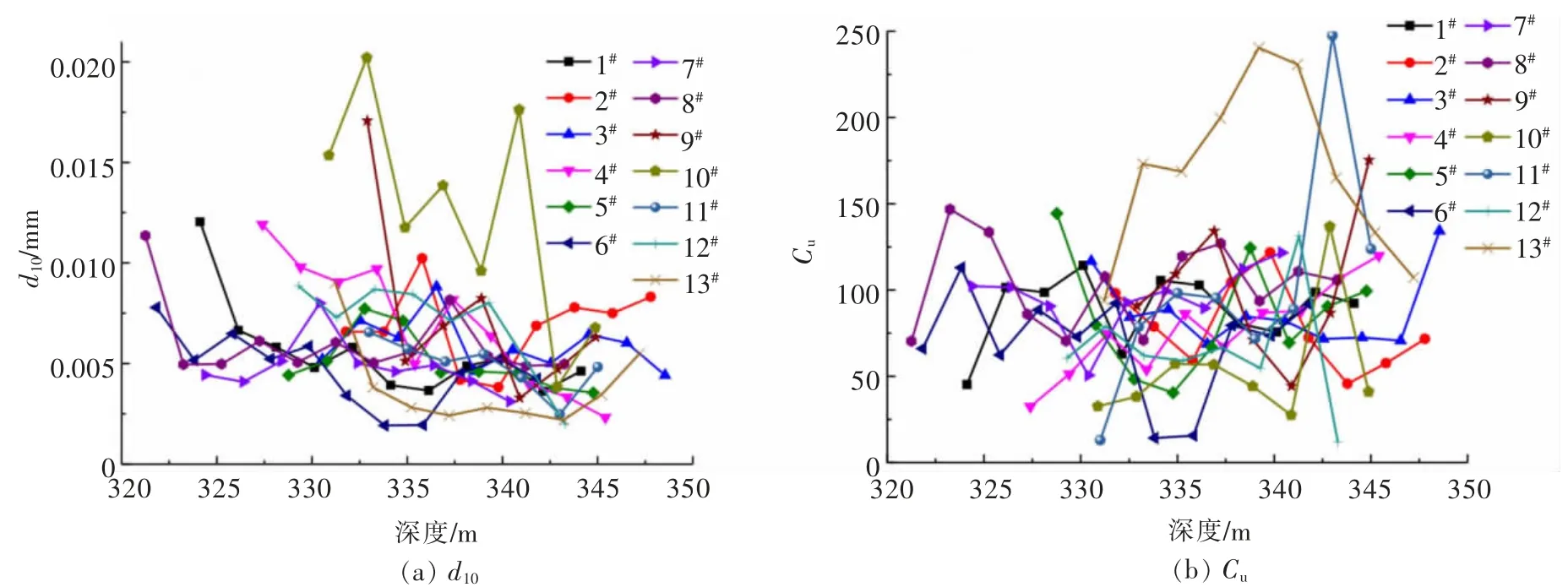
图7 离子型稀土矿土d10 和Cu 测试结果Fig. 7 The test results of d10 and Cu in ionic rare earth ore

以图8 的计算结果为基础，分析变异函数（γ）随两点间距（h；步长取10 m）的关系，结果如图9 所示。从图9 中可知，变异函数的块金值不为0，且渗透系数自相关范围小于40 m。 采用常用的线性有基台模型、球状模型、指数模型和高斯模型[24-25]（模型的表达式依次为式（9）—式（12））分别拟合图 9 中 h＜40 m的数据。

图8 取样点处渗透系数的估算结果Fig. 8 Estimation results of permeability coefficient at sampling points

式（9）—式（12）中：γline（h）、γspherical（h）、γexp（h）和 γgauss（h）分别表示线性有基台模型、球状模型、指数模型和高斯模型的变异函数；C0为块金值；C0+C 为基台值；a为变程。

经拟合计算，结果列于表4 和图9。其中，球状模型拟合效果较好，决定系数R2达0.931；而高斯模型的拟合效果较差，其决定系数R2仅为0.727。 可见，采用球状模型作为计算渗透系数空间分布的变异函数是较优的。

图9 变异函数（γ）随取样点间距（h）的关系Fig. 9 Relationship between variation function（γ） and sampling point spacing （h）

表4 变异函数拟合结果Table 4 Fitting results of variance function

3.3 研究实例分析

以球状模型作为变异函数，采用上述建立的渗透系数空间分布计算方法 （计算流程如图10 所示），基于图8 所示取样点的渗透系数，采用普通克里格法计算渗透系数的空间分布（图11）。 可知，渗透系数具有明显的空间变异性； 平均渗透系数的平面分布（图12）也显示，在地形右上角的区域，矿体的渗透性较好；在相同情况下，该区域的浸矿剂消耗量明显少于低渗透性区域。

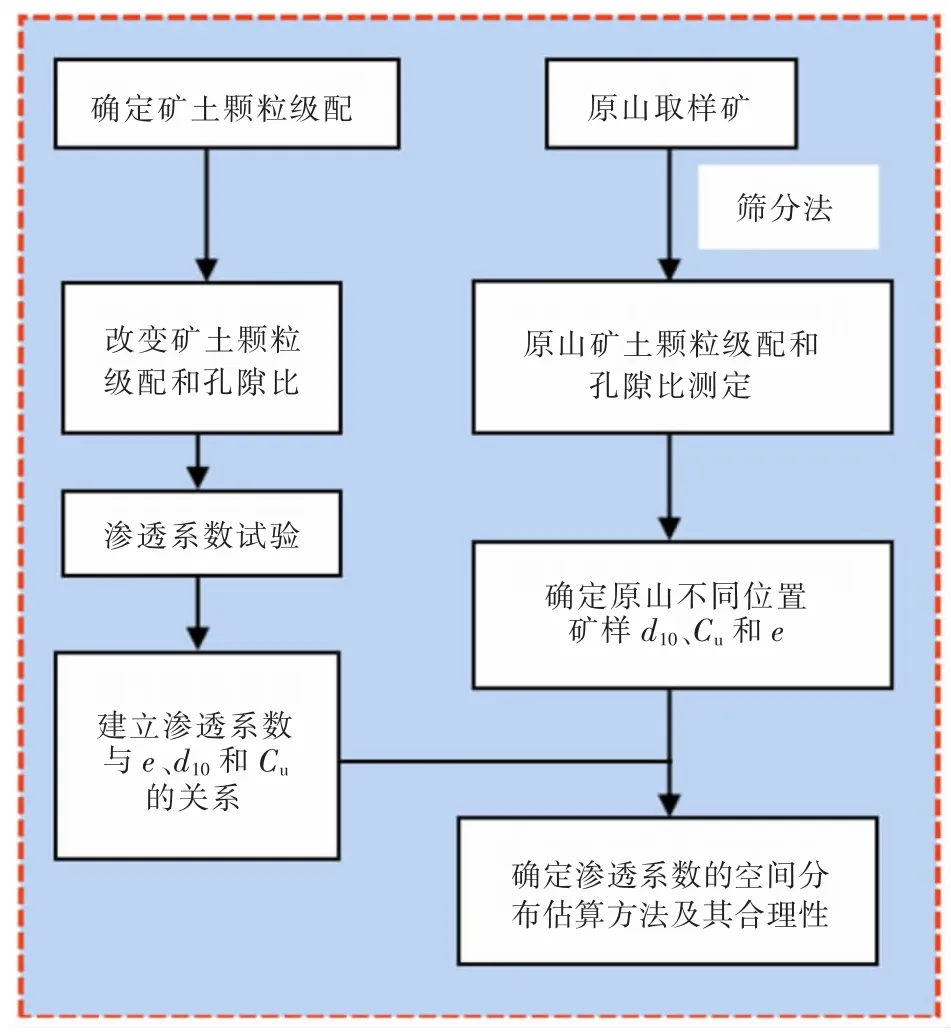
图10 矿体渗透系数空间分布计算流程示意Fig. 10 Calculation flow chart of spatial distribution of permeability coefficient of ore body

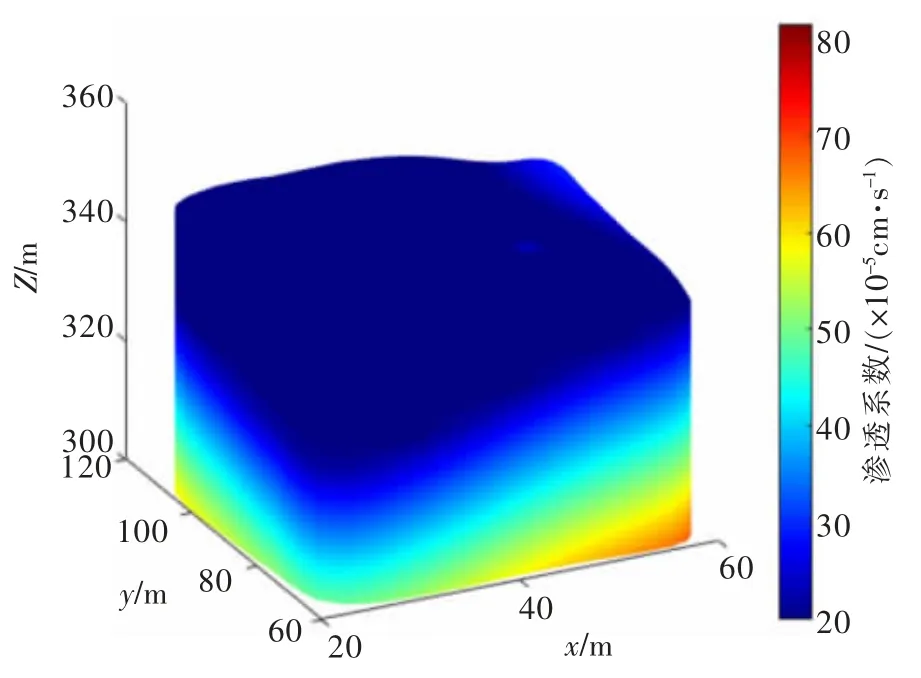
图11 渗透系数的空间分布Fig. 11 Spatial distribution of the permeability coefficient

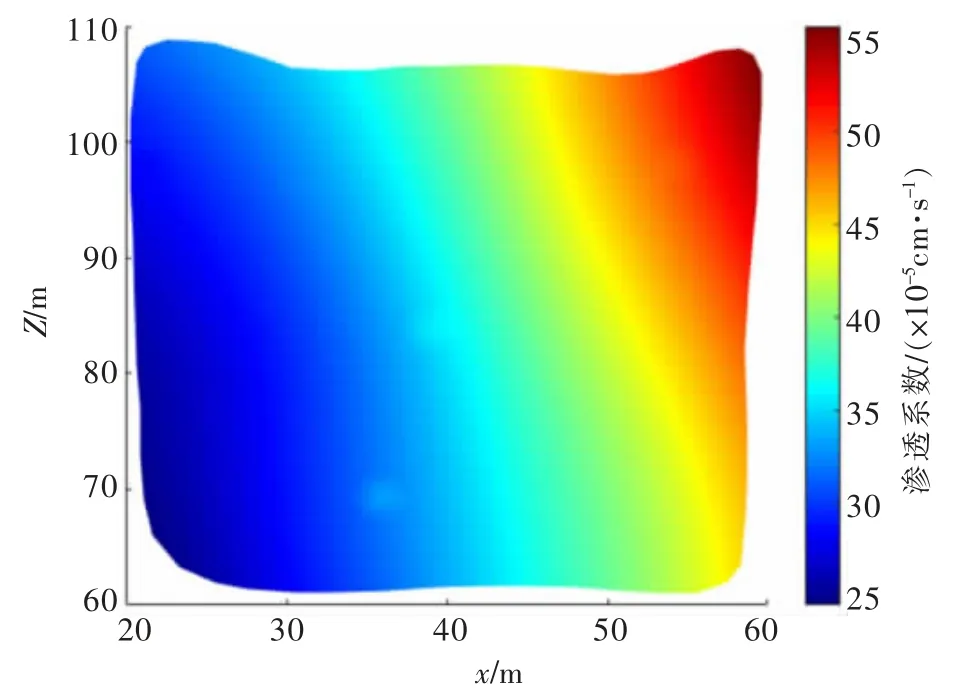
图12 平均渗透系数的分布Fig. 12 Distribution of the average permeability coefficient

4 结 论

1） 稀土矿（土）渗透系数（k）的对数随孔隙比（e）、d10和不均匀系数（Cu）的变化性均可以采用线性函数进行量化表征， 拟合的决定系数均大于0.800，且e、d10和Cu相互间对斜率影响的变异系数小于20.0%，这3 个参数是线性相关的。

2） 本次建立的渗透系数计算模型为k=105.16e+240.97d10+9.72×10-3Cu-10.51，相比于试验数据，计算渗透系数的相对误差仅为15.1%，反映本模型是合理的。

3） 建立了渗透系数空间分布的计算方法， 指出普通克里格法的球状模型计算变异函数的精度较高。 经实例分析证实，该方法计算的渗透系数与实际吻合较好。