生命表法在古人口学中的应用误区

侯侃

摘要：生命表是古人口学发展早期的常用方法，但历来受到许多质疑。其问题主要有：死亡率误区和队列假设的影响，静止人口假设或稳定人口假设问题，模型生命表存在的问题，人骨年龄估计问题和抽样缺陷问题。生命表的意义主要在于其可以直观展示古人口的死亡过程和计算古人口的预期寿命。目前在古人口学中，生命表已逐渐趋于淘汰，而以风险模型为代表的其他方法成为了研究古人口死亡模式的新方法。

关键词：古人口学；生命表；死亡模型

1 引言

生命表（life table） 是一种现代人口学中常见的人口统计方法，是利用模型思想以人口的死亡率为核心构建的人口死亡模型。生命表记录了同一个队列（cohort） 的人口从出生到死亡的整个生命过程，反映出人口随着年龄增长的死亡过程，所以也被称为死亡表。同时，它也反映人口的寿命过程，可用于计算人口的平均寿命，因而还被称为寿命表[1]。

生命表在古人口学中的应用有着较长的历史，是早期的主要方法。1969 年LawrenceAngel 发表了对古人口学方法论的认识，从此在体质人类学中开创了古人口学这一分支学科，此文中最早提到了生命表法，但并未予以实践。从20 世纪70 年代起，古人口学界主要在两个方面开展工作，一是将人口学理论应用于古代人类，二是把生命表作为解读考古出土人骨样本死亡年龄数据的一个重要工具[2]。1970 年，匈牙利人口学家Gyo?rgy Acsa?di 和人类学家Ja?nos Nemeskéri 合著的《人类寿命和死亡率的历史》[3]，将生命表正式应用于古人口学实践中，并且建立了早期生命表的研究范式。他们依据出土人骨鉴定所得性别、年龄数据，编制了欧洲上百个遗址的生命表，并由此得出中欧地区新石器时代人类预期寿命呈增长趋势这一认识。这部专著不仅是古人口学中生命表应用的开山之作，更是古人口学乃至体质人类学发展史上里程碑式的作品，一经问世便引起学界高度关注并纷纷效仿，成为很长时间内古人口学研究的模板。在美国，生命表从20 世纪70 年代起流行起来，众多学者陆续对此展开讨论[4-10]。

在中国，直到20 世纪90 年代才出现古人口学的专门研究，例如辛怡华对元君庙仰韶墓地人口结构的研究[11] 和陈铁梅对新石器墓葬成年人骨性别比异常问题的研究[12]。使用生命表则始于20 世纪末潘其风、韩康信和朱泓等学者各自撰写的人骨研究报告[13-15]，当时是非常新颖的方法，后来被广泛应用[16-19]，所使用的生命表编制方法一直未变，直至近年来才有学者使用模型生命表对编制方法进行了改进[20]，另外还有学者对生命表在古人口学中的应用和局限性进行了探讨[21，22]。

生命表这种方法由Angle 在1969 年首先引入到古人口学研究中，虽然同时他也表达了一些质疑，但其后还一度成为研究古人口死亡模式最有用的方法[23]。在1975 年人口学家Peterson 对古人口学进行全面批评[24] 后，这类质疑开始变得不绝于耳，20 世纪80 年代中期以后质疑之声就更多了[25，26]。本文旨在回顾和总结生命表在古人口学发展历程中受到的种种质疑，并简要介绍古人口学研究方法的发展和改革，以供参考。

2 死亡率误区与队列假设的影响

生命表的编制一般采用的是假设队列方法，而不是真的去追踪一个人群从生到死的整个过程。“队列”（cohort） 是人口学中的一个关键概念，指的是特定时期内共同经历某个人口事件的所有个体的集合，在生命表中用到的是出生队列的概念，即同一时期内出生的个体的集合[27]。

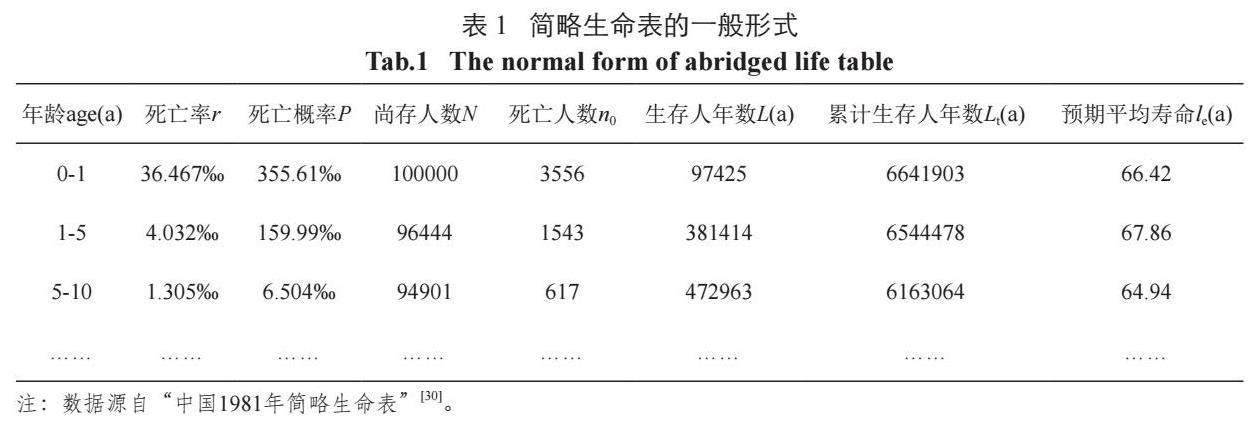
在假设中，需要假定生命表中各年龄组死亡率等于某一时期的各年龄组死亡率。表1 所示的是简略生命表（即以5 岁为一个年龄组的生命表）的一般构成，编制生命表的过程即在上述假设的基础上按照从左至右的顺序填充该表格的过程[28]。年龄别死亡率r=（n0/n）×1000‰，其中，n0 为某年龄组的死亡人数，n 为某年龄组的平均人数。年龄别死亡概率P=（n0/N）×1000‰；

其中P 指的是一批人在一个年龄段死亡的概率，N 指的是尚存人数。n0 和N 都是未知的，因此不能直接计算死亡概率，需要用死亡率来推算，公式为

P=r/[1+（1-l）r]×1000 ‰ （1）

式（1） 中，l 是1 年期间死亡人口的平均寿命。对于1 岁及1 岁以上组，通常假定死亡分布是均匀分布，则l=d/2，d 是年龄组的跨度；对于0 岁组，则通常将平均寿命l 取其他的数值，方法很多，各有不同[29， 30]。

在完成对年龄别死亡概率的估算后，可继续对剩余指标进行计算，在此不一一详述，读者可参阅各类人口统计学教材。需要指出的是，其中尚存人数N、死亡人数n0 的计算都需要用到P 这一数值，而生存人年数L 则又需代入l 的数值来计算。累计生存人年Lt要用L 数据来计算，预期平均寿命le 用Lt 除以N 得到。可见，死亡率r 在整个生命表的编制中有着不可替代的核心地位，如果该数据缺失，则生命表将无法编制；如果该数据有误差，则整个生命表都将出现误差。由于我们无法观察一批人从出生到全部死亡的全过程，因此在编制生命表时，依据的都是某一年或几年平均的死亡率。如此一来，生命表就成了假定有一批人在一生中的各个年龄都按照某一死亡率死亡所出现的结果[31]。

那么古人口学中一般是如何获知死亡率数据的呢？死亡率表示的是一个人口的死亡强度，是一个人口年内死亡人数与年人口均数或年中人数之比[32]。

生命表中每个年龄组的死亡率从理论上讲应该通过人口调查统计得到，用该年龄组的死亡人数除以该年龄组的年均人口数（即某年内某个时点的人口平均数），然而这在进行人口调查时一般是难以获取的，因此一般用年中人口数来代替。然而，在古人口学中，如何计算死亡率就成了一个难题，因为我们只知道一个年龄组的死亡人口数，却不知道该年龄组的存活人口数，相当于只知道死亡率计算式的分子，却不知道分母。

前文曾提到国内学者数十年来基本上都沿用相同的生命表编制方法。在他们的实践中，通常不计算死亡率，而是直接计算死亡概率P，做法是将人骨样本中某年龄组死者个体数作为n0，将人骨样本中此年龄组之后的个体数的总和作为N。这样一来，n0 和N 都不是通过死亡率计算出来的，而被认为是已知数值，大大地简化了生命表的编制过程。其中，0-1 岁组在计算生存人年数时没有考虑到d≠1/2，而是还将其当作1/2 来计算，这显然是错误的。这直接造成了出生时预期寿命的计算结果不等于平均死亡年龄，且前者均高于后者。实际上，我们所做的这种生命表相当于是建立在静止人口假设的前提下的（后文会详述此问题），静止人口的出生时预期寿命必然等于平均死亡年龄[33]。

古人口学研究的对象一般是一个墓地或遗址中出土的人骨的总和，这些人骨可以被视为人口学研究中的死者，但不符合队列的概念（他们的出生年代跨度可能非常大，这取决于该墓地或遗址的使用时长）。在人口学中，同批人出生的“同时”通常只能涵盖一个较短的时间段，一般是一年，因此用来编制生命表的对象一般都是某年的某人群，至少是同一代人。而常见的年代跨度较大的考古样本，相当于是把若干代人合并成了一个“队列”（至少也是把出生年份差距较大的人合并成了一个“队列”）。在这种情况下，一个人骨样本中某年龄组死者个体数可能是不同代的死者，而其中每一代死者死亡时还存活着多少人（即N）是无法得知的[34]。综上所述，死亡率的构建是基于队列假设为现代人口统计开发的方法，在考古样本中难以获得。

3 关于静止人口或稳定人口假设

静止人口指的是人口没有增减，或者增减保持平衡，每年的出生人口数恒等于死亡人口数[35]。只有当人口是静止且封闭的情况下，将骨骼样本的死亡年龄分布视为等效的n0 列才是合理的，在这种情况下，每年在每个年龄组中死亡的人数和比例保持不变，死亡年龄分布保持不变，并且所得的骨骼样本可以被视为出生队列[36]。在二十世纪六七十年代，许多古人口学家就是在静止人口假设的前提下进行的生命表重建。例如Acsa?di 和Nemeskéri 的研究认为，在人类历史的大部分时间里，人口的长期增长率非常接近于0[3]。

在古人口学发展的早期，生命表的静止人口假设就已经被认为是有问题的[37]，因为如果忽视增长率，将死亡年龄数据直接转换为年龄别死亡率，不去独立地验证静止人口假设是否为真，就是武断的、有误导性的做法，会严重歪曲研究结果[35，38]。考古样本往往只是一个上百例甚至不足百例的小规模人口，而人口规模越小则增长波动会越大。比如对近现代狩猎采集人群的人口学调查发现，小规模人口增长的短期潜力通常很高，其人口增长率每年可以高达0.5%～2%[39]。许多古人口学家也表示质疑：如果所有的古人口都一直保持静止，那么人类如何能发展到现在这么多？显然这一前提条件几乎不可能符合实际[33]。在1992 年，“骨学悖论”一文中详述了人口的非静止性[40]，自此以后古人口学研究再也不用静止人口假设了。

另一种假设是稳定人口假设，也是生命表最常用的假设。稳定人口指的是人口总数每年按固定比例增加或减少，即出生率和死亡率保持恒定 [34]。有学者认为，稳定人口假设可能更适合古人口，因为其所受各种条件限制要比静止人口少得多，即便是生育率和死亡率发生变化，且存在人口迁移的情况下，大部分人口仍会在任意时间点都非常接近稳定人口的状况，这种特征被称为稳定人口具有“弱遍历性”，确保了基于稳定人口假设的模型总能得到良好拟合，除非人口样本正在经历异乎寻常的快速且剧烈的变化[41]。

稳定人口假设同样存在明显缺陷。首先，人口增长的稳定态是难以保证的。Angel 早在1969 年就指出假设人口在墓地使用期间保持稳定是错误的[23]，人口的增长波动尤其在小规模人口中更显著，其原因与质疑静止人口假设的原因相同。其次，人口增长一旦有波动，哪怕这种波动非常小，也会对生命表造成显著影响。Moore 等人发现，人口的自然增长率对生命表的影响很大，他们通过对给一组人口数据设定不同的增长率，发现即便增长率的差异只有1%，也会使计算所得的预期寿命出现显著差异，这种差异在越小的年龄组越明显，出生时预期寿命的差异是最大的，同时这也造成了在统计学意义上有显著差异的生命表的死亡率有可能相同[9]，如此便失去了对不同人口的生命表进行对比的意义。Bonneuil研究17 世纪的人口记载后发现，稳定人口假设并不适用于过去的人口，因为人口的生育率和死亡率是显著可变的[42]，而且人口的变化经过长期累积也不能产生与稳定人口相似的死亡年龄分布[43]。对若干现代狩猎采集人群的研究同样发现了死亡率的可变性，即便两个人口出生时预期寿命差距不大，45～49 岁组的预期寿命仍可出现显著差异[44]，这种情况暗示了不同年龄段的死亡率可以不同，因此假设死亡率恒定并不现实。

4 模型生命表存在的问题

在人口学中，模型生命表用于估计人口统计数据不完整或有缺陷的情况下的死亡率，即在模型生命表中找到一个n0 列与样本中观察到的死亡年龄分布相匹配的生命表，然后就可借用该模型的其他人口统计指标（比如死亡率、增长率等），作为样本的相应指标，进行生命表的编制。模型生命表建立在稳定人口假设之上。Bennet[5] 和Weiss[6] 最早提出了基于稳定人口假设的模型生命表，前者使用了Carrier 建议采用的1956 年联合国模型生命表[45]，数据源自对现代人口的统计调查；后者使用了根据民族学调查所得的原始族群生命表，和根据历史文献记载所得的部分西方地区古代和近代的历史人口生命表。后来，学者们陆续开始使用联合国后续发布的模型生命表，主要代表为Coale-Demeny 模型生命表，一般选用其中的西区模型生命表。

从理论角度来看，用模型生命表拟合古人口样本建立在人口的均变论假设之上。

Howell 认为，史前人口的模型生命表和生育时间表可用于插值或修匀生育率和死亡率数据，这是因为与生育率和死亡率有关的生物学过程在不同的人口当中都是相似的，遵循一致的自然规律[46]。人口的均变论假设是古人口学的核心假设，一直备受质疑[47]，质疑者认为采用均变论假设是一种“自我实现的预言”（self-fulfilling prophecy）[48]。当使用骨骼形态特征来估计骨骼遗骸样本的死亡年龄时，由此产生的年龄分布往往显示青壮年和中年占比较大，60 岁以上占比则明显较小。这种异常模式不见于现代人口模型生命表中，也没有在现代的狩猎采集或原始农业群体中表现出来，这种情况暗示均变论假设不一定适用于史前人口[49]。

从实践角度来看，单个古人口的死亡年龄分布通常可以匹配多个模型生命表，它们可能具有差别很大的死亡率、生育率和增长率，并不一定能确定哪种模型生命表是最合适的[50]，而且模型生命表对古人口样本而言也未起到很好的拟合效果。早在1977 年，Bocquet-Appel 就发现，人口统计学家根据现生人口调查数据所得的模型生命表不适合前工业化时代人口的死亡率特征[51]，后来许多学者也有类似结论[52-54]。民族志人口统计[55]和历史人口统计[56，57] 的结果证实了这一点。

模型生命表实质上是一种非参数模型，与参数模型之间的差距在于其不包含参数，而是给定了一组死亡率作为常数，因此减少了可能性。如果模型生命表是可靠的，那么它所包含的多种死亡模型中必须有一种能很好地吻合待研究人口的实际情况，这显然是成功概率很低且无法验证的[58]。另一方面，这种方法相当于指定某种模型作为被研究的古人口的死亡模式，而如果将这种模型统一选定为一种，比如前面提到过的Coale-Demeny 西区模型生命表，就相当于是把古人口都固定成了同一种死亡模式。但是我们研究古人口就是为了探索过去不同人口发展模式的差异，将之与其他考古学资料相结合来探讨考古学问题，若是为了“较科学地”获取生命表数据，就将不同人口的死亡模式锁定成一种，那我们研究的意义何在呢？模型生命表所代表的死亡率模式的多样性显然是不够的，它们是从有限数量的现生人口中得出的，可能对样本人口赋予了不符合实际的人口模式[22，59]。比如在Coale-Demeny 模型生命表中，只有7% 的人口数据是1870 年以前的，且没有一个是欧洲以外的[60]。

5 人骨年龄估计误区

人骨的年龄估计是古人口学的一个关键问题，依据考古出土人骨鉴定得到的年龄数据是研究的基础。影响生命表编制的年龄估计问题有三个：

第一是成人骨骼的年龄鉴定不可靠。未成年人的骨骼和牙齿生长发育遵循的是基因规律，鉴定的准度和精度相对成人较高[61]，所以只要未成年骨骼保存情况较好，鉴定结果一般都能达到编制简略生命表的需求。然而成人骨骼的年龄鉴定存在很大问题，比如“年龄的模拟效应”[62] 造成了年龄的低估倾向，会使计算所得预期寿命被缩短[26]。

第二是老年人年龄无法准确估计。一方面，年龄越大的个体，年龄估计的误差范围就越大[63]，容易造成估计结果的区间范围超过5 岁；另一方面，现有的各种常用的形态观察法，例如用耻骨联合面、髂骨耳状关节面[64]、颅骨骨缝[65]、肋骨末端[66] 等部位来判断年龄的各种标准，都无法准确地判断60 岁以上老人的年龄，一般只能以“60 岁以上”这样的开区间年龄段作为鉴定结果，这种数据显然不能用于生命表的编制。在古人口学编制生命表的过程中，经常把60 岁以上个体全部纳入末尾的60～65 岁年龄组，这并不符合实际。有的个体很可能超过65 岁，这会导致低估老年人的年龄，进而降低成年人的预期寿命，造成古人口的年轻化假象[67]。此外，这种方式不仅会造成生命表计算结果失真，还会对解释古人口造成严重影响，因为老年人的存在对研究亲属关系、居住模式、儿童保育和知识的传授具有重要意义[68]。

第三，鉴定所得的年龄段不是一个固定的区间，且区间宽度往往难以符合生命表的需求。简略生命表至少需要不大于5 岁的年龄区间，而实际鉴定所得结果往往区间范围过大（比如30～40 岁、20～40 岁），这种数据无论怎么处理都会对生命表的客观性构成显著影响。

6 抽样缺陷误区

人骨样本的形成本身就是一个抽样过程，主要分为五个步骤：第一是从活着的人到死尸；第二是从死尸到被埋葬者，有些尸体不会被埋葬；第三是从被埋葬者到人骨遗存，有一些被埋葬者是无法留下人骨遗存的；第四是从人骨遗存到考古出土人骨，即考古发现人骨并发掘的过程；第五是从考古出土人骨到被研究的人骨，因为许多可能的原因，研究者不一定有机会研究出土的全部人骨[22，34]。上述五个步骤，每一步都是抽样的过程，而且不一定是随机抽样。

第一步过程中存在的抽样问题是由“骨学悖论”中提出的“有选择的死亡”效应所造成的，即成为死者的个体是存活人群中“最容易死”（或者说是最脆弱）的个体[38]。这造成了古人口学研究的每个年龄段都是当时存活的人群中该年龄段最容易死的那些人组成的，而相对不容易死的个体则活到了之后的年龄段。这一点虽不会对生命表的编制造成影响，但是会对解释生命表构成影响。例如对预期寿命的解释，由“脆弱者”构成的人口的预期寿命比对现生人口调查所得的预期寿命短就成了正常趋势。

第二步反映的是古人的埋葬习俗。不论古今，均存在着将具有不同属性的人埋葬在不同地点的习俗，例如不在公共墓地埋葬婴幼儿。另外还存在不土葬死者，而是用火葬、水葬、天葬等方式处理尸体的行为，这些现象都会造成这部分个体在生命表中的缺失。

第三步指的是尸体的埋藏过程。骨骼样本保存的数量和质量会对人口样本的抽样造成影响，这是古人口学自诞生之日起就难以解决的困难[69]。在不同的埋藏环境中，尸体遭到的破坏是不同的，但相同的是，骨骼细小脆弱的婴幼儿个体最容易遭到破坏，最终使人骨样本中这部分个体缺失，加上上述埋葬习俗的影响，共同造成“婴幼儿缺失”现象[23]。无视这一现象去编制生命表的话，会产生一定的误差[9]。

第四、五步是考古工作者所造成的，这类抽样过程大多是非随机的。例如部分考古工作中只将保存相对较好的骨架予以收集或研究，实际上就是主观筛除了保存相对较差的个体，是具有明确筛选条件的非随机抽样。一些发掘者经验有限，无法辨识出细小的婴幼儿骨骼，或者由于工作不够细致，未能以细筛筛选出婴幼儿骨骼[70]，这两种因素也都是非随机抽样，会加剧“婴幼儿缺失”问题。

样本量问题也属于抽样问题。人口学研究的对象相对于古人口学来说是规模很大的人口样本，这导致研究中存在这样一种倾向：哪怕是非常微小的数据变化也是有意义的。如果样本量太小，比如古人口学中常见的最多只有几百人规模的样本，可能就会因为样本量小更容易出现数据的随机波动而令误解产生。Moore 等通过计算机模拟发现，编制古人口样本的生命表是一个概率问题，小样本人口死亡概率的标准误与样本量成反比，如果不能降低这个标准误，就会使不同生命表之间的差异只能体现出数据的随机波动，而不能反映任何有意义的问题，比如文化因素或其他生物学因素[9]。Paine 用年龄已知的人骨材料模拟出的180 个样本分析发现，无论是在生存人口结构还是死亡模式上，小样本（样本量小于100）都会服从于随机分布，随机过程的影响与样本规模成反比，而绝大多数考古发现的骨骼群体都属于“小样本”[71]。Hoppa 和Saunders 同样进行了类似的随机抽样模拟实验，评估不同样本量下随机人口的死亡年龄分布，发现由100 人以下的个体组成的样本的死亡年龄分布的变异度非常高。若对模拟人口分性别进行统计，则会发现当样本量小于100 时，两性平均死亡年龄与真实数值的差异会相当大，甚至达到15 岁之多，因此认为少于100的样本量不能可靠地反映人口的真实情况[72]。

7 生命表的意义及克服缺陷的策略

对于考古学研究来说，生命表并不能为考古学研究提供直接有效的信息，因为我们无法确定是哪些因素导致不同古人口的生命表数据出现了差异，但它可以作为一种基于稳定人口假设的人口模型，并纳入到尺度更大的生态和文化过程模型之中，成为一种研究手段[9]。

对于古人口学来说，生命表的意义主要有两点：第一，直观展示古人口的死亡过程，了解到一个古代人群不同年龄段的死者比例，进而结合其他考古信息讨论其成因。第二，计算古人口的预期寿命。这个预期寿命不同于死亡年龄的概念，我们经常计算的平均出生时预期寿命也不同于平均死亡年龄，前者指的是用死亡率数据估计出来的一个生存队列出生后剩余生存年数的预期值的平均数，后者则是一个人口中死者年龄的平均数。在人口学当中，一般认为后者意义较小，因其不能反映人口的死亡率水平，而死亡率水平才是衡量人口寿命高低和健康水平的关键指标。

对生命表的诸多误区或缺陷来说，如何克服它们是该方法发展多年来学者们的迫切任务，近三十年来在克服年龄估计缺陷方面的进展尤多。关于克服年龄鉴定中存在的年龄区间不确定问题，Ubelaker 认为可以用加权的方法对各年龄段的生存人数进行调整，具体操作是：将年龄鉴定较可靠、年龄区间较窄的个体在各年龄段所占比例作为权重，附加于年龄鉴定结果的区间超过5 岁的个体之上，把这些个体的计数按上述权重分配到生命表的各年龄组中[73]。这种操作方法虽然简单，但显然存在无法验证的问题，可能不仅没有正面效果，反而会更加背离实际。还有学者提出，可以借用蒙特卡罗模拟的思想在每具人骨鉴定所得的年龄范围中随机提取一个年龄数值，用以构建生命表，只要重复抽取的次数够多，就可以构建具有较强稳健性的生命表的可能范围（即哈雷带“Halley band”）[74]。另一方面，为了克服年龄的模拟效应，过渡分析（transition analysis） 应运而生，它同时也能解决老年人年龄估计结果不确切的问题[75]。不过，如何获取死亡率、队列假设和稳定人口假设等问题则是无法解决的，因为这些问题都根植于生命表的本质，是生命表中不可或缺、无法替代的基本要素和编制生命表的前提。

死亡年龄分布是我们从人骨样本中能直接得到的，它主要受到了生育因素而不是死亡因素的影响。换句话说，人口死亡年龄分布的主要成因是生育水平而不是死亡率水平。死亡力（the force of mortality） 在所有年龄范围内都起作用，而生育率的影响则集中在出生这一刻。古人口学界最晚自20 世纪80 年代起就知道了这一点[33，36，76]。生命表的本质是死亡率的数学模型，是死亡因素的集中体现。那么显然，由人骨样本所得到的死亡年龄分布与生命表的关系因此就变得十分疏离。如今国际古人口学界已经更多地倾向于对古人口的生育水平进行研究[37，77]，也正是基于这一原因。

总的来说，生命表在古人口学中的意义颇具局限性，再加上本文所述诸多误区，故而生命表在古人口学中的重要性越来越低，已不属于当前的主流方法。目前国际上对死亡模式研究的改革，主要是用到了参数模型，这可以替代传统的生命表方法。这种方法用多种死亡率模型（如Gompertz 模型、Gompertz-Makeham 模型、风险模型等）来估计出生队列死亡年龄的概率密度函数和生存函数，进而推导出年龄别死亡率[78]。其中风险模型（hazard model） 受到了一些学者的推崇，成为替代生命表的主流方法[79，80]，TimothyGage[81，82]、James Wood 等[83] 对其进行了详细介绍。比较常见的风险模型是Siler 五参数竞争风险模型[84]，可以用它对生命表做出改进，即对原始生命表进行模型拟合，用最小二乘法或最大似然法进行参数估计。该模型的死亡率函数为：

rt=r1exp（-R1t）+r2+r3exp（R3t） （2）

式（2） 中，rt 是年龄为t 时的瞬时死亡率，或者称为由公式右侧三项竞争风险因素造成的年龄为t 的队列的死亡率，它由三部分组成，即等号右侧由加号相连接的三个部分。第一部分代表了这一队列在未成熟期的死亡率，其中r1 是出生时的死亡率，R1 是未成熟期死亡风险随年龄增长而降低的比率；第二部分，即r2，是不随年龄增长而改变的恒定的死亡率，这部分一般称为死亡率的残差，它被作为Gompertz 死亡率模型中的附加部分；第三部分是Gompertz 死亡率模型，这里被扩展用于修匀和改善成年期的死亡率估计，代表了死亡力的老年部分，其中r3 是老年期的死亡率，R3 是老年期死亡风险随年龄增长而增加的比率。这种模型模拟了所有已知的人类死亡率的年龄模式，即死亡率会在生命的最初几年迅速且持续地下降，到10～15 岁时达到最低值，之后又持续上升[46]。全人类乃至各种哺乳动物，其死亡率的年龄模式都遵循这一普遍模型[80，85]，不同地域的人群或不同物种在相同年龄层的死亡率变化基本模式一致，只不过死亡率曲线的起伏程度有所不同，因此这种模型具有极其广泛的普适性，是整个人口学界普遍认可的规律，被称为Gompertz-Makeham 死亡率定律[86]。根据Gage 对三组古人口样本的实践检验，发现这种方法不会在人口数据上施加特定的死亡率，并能较好地还原古人口真实的死亡模式，主要优点在于其可以帮助修正有缺陷的数据，并修匀由于样本量小而导致的特定年龄段死亡率的随机波动，并且可以借助此方法直接根据古人口性别年龄数据估计死亡率和生存率等人口学指标[80]。根据用Coale-Demeny 模型生命表进行的拟合优度检验结果，证实这种模型具有很高的拟合度[81]。陆续有学者对此法进行了实践[87-91]，其中在Nagaoka 对日本中世纪考古遗址人骨的实践中，发现该方法很好地修正了因为婴幼儿缺失造成的低龄阶段死亡率偏差[88]。

其他新方法还有Cox 比例风险模型[92] 等半参数模型，这种方法可以估计死亡风险和各种因素对死亡风险的影响。还有一些非参数方法，例如Kaplan-Meier 生存分析和使用模拟退火（simulated annealing） 优化算法来估算人口学参数的方法等，前者可以被应用于比全参数方法所需的样本量更小的样本上，一些学者[89， 93-97] 对此方法进行了成功实践；后者则用非常复杂的数学方法使分析不稳定的人口变得可能，但该方法由于难度过大，目前只有提出者进行过实践[43]。

由于样本的特殊性，古人口学研究必须建立在一定的假设上，基本假设即生物均变论[46] 和人骨样本具有代表性（称为Whopper 假设）[23]。生命表则需建立在静止或稳定人口假设之上，为其又增一重假设。假设越多，结果就越不可靠，这是自然之理。时至今日，这些都是困扰学界的难以满足的假设条件。由于多重假设和误差的存在，我们应十分审慎地看待古人口学的研究结果。在《古人口学21 世纪宣言》一文中，French 等学者强调要采取多学科、多方法相结合的方式发展古人口学，认为古人口学参数可以从各种来源获取，包括生物人类学、基因组学、历史学和考古学，若干个指标的集合可以弥补单个指标的局限性，同时也建议我们应该重视对古人口学基本假设和人口模型的讨论，毕竟如果假设或模型本身就有问题的话，研究也将是误导性的[98]。

在古人口学研究的具体方法上，需要重视抽样问题和人骨样本与现代人口调查样本在诸多属性上的不对等所带来的负面影响，两者都可能造成许多人口统计学方法和人口学理论的不适用，抽样问题还会造成材料不一定能客观、全面地反映实际。为了解决这些问题，学界主要从两个角度对研究方法予以发展：第一是研发专用于古人口学的、有别于已有的人口统计学方法的新方法，例如许多学者提出的一些与生育率等动态参数强相关的指标[99]，用以规避婴幼儿缺失和老年人年龄估计不准问题，以及采用重新抽样（resampling）[100]和计算机模拟[101] 等数学方法处理样本量较小的材料；第二是将目光从单个遗址的个案研究转向更大的时间、空间尺度下的大规模研究。Konigsberg 提醒我们：“相当多的努力短视地集中在单个遗址或一小组遗址所构成的古人口上，往往试图将生命表参数的微小变化与生存或健康的变化联系起来。这些个案历史本身很有趣，但只有在更广泛的分析水平上，我们才能开始看到古人口学的共性”[102]。这是重视扩展研究尺度的一种观点，以Bocquet-Appel 为代表的学者对新石器时代人口变化的研究[103] 非常符合这一理念，成果得到了考古学界的广泛关注。

在此，本文呼吁学界能够更多地关注古人口学研究中的理论与方法问题，而不只是将关注点放在材料和结论上，尤其要避免预设结论的研究，加强对方法的思考，加强多学科合作，否则我们对材料的解读就可能是有很大问题的。

致谢：感谢两位匿名审稿人的建设性意见，他们为本文的完善做出了重要贡献。

参考文献

[1] 郭未．人口学[M]．北京：社会科学文献出版社，2018， 248-250

[2] Hoppa RD. The Once and Future Palaeodemography[M]. Toronto： University of Toronto， 2001

[3] Acsádi G， Nemeskéri J. History of Human Life span and Mortality[M]. Budapest： Akademiai kiado， 1970

[4] Lallo J. The Paleodemography of Two Prehistoric American Indian Populations from Dickson Mound[D]. Amherst： University ofMassachusetts， Amherst， 1972

[5] Bennett KA. On the estimation of some demographic characteristics on a prehistoric population from the American Southwest[J].American Journal of Physical Anthropology， 1973， 39（2）： 223-231

[6] Weiss KM， Wobst HM. Demographic models for anthropology[J]. Memoirs of the society for American Archaeology， 1973， 27： 1-186

[7] Howell N. The feasibility of demographic studies in “anthropological” populations[A]. In： Crawford M， Workman P （Eds）. Methodsand Theories of Anthropological Genetics[M]. Albuquerqu： University of New Mexico Press， 1973： 249-262

[8] Green S， Green S， Armelagos GJ. Settlement and mortality of the Christian site （1050 AD-1300 AD） of Meinarti （Sudan）[J]. Journalof Human Evolution， 1974， 3（4）： 297-311

[9] Moore JA， Swedlund AC， Armelagos GJ. The use of life tables in paleodemography[J]. Memoirs of the Society for AmericanArchaeology， 1975， 30： 57-70

[10] Lovejoy CO， Meindl RS， Pryzbeck TR， et al. Paleodemography of the Libben site， Ottawa county， Ohio[J]. Science， 1977，198（4314）： 291-293

[11] 辛怡华．仰韶文化人口自然结构初探：从元君庙墓地看仰韶文化的人口自然结构[J]．人口研究，1990， 6： 48-52

[12] 陈铁梅．中国新石器墓葬成年人骨性比异常的问题[J]．考古学报，1990， 4： 511-522

[13] 潘其风．大甸子墓葬出土人骨的研究[A]．见：中国社会科学院考古研究所（ 编）．大甸子：夏家店下层文化遗址与墓地发掘报告[M]．北京：科学出版社，1998， 224-322

[14] 韩康信．山东兖州王因新石器时代人骨的鉴定报告[A]．见：中国社会科学院考古研究所．山东王因：新石器时代遗址发掘报告[M]．北京：科学出版社，2000， 388-413

[15] 朱泓．建新遗址新石器时代人骨的鉴定报告[A]．见：山东省文物考古研究所．枣庄建新：新石器时代遗址发掘报告[M]．北京：科学出版社，1996， 221-223

[16] 张君，王根富．江苏金坛三星村新石器时代墓葬中的人口统计与研究[J]．文物，2004， 2： 54-60

[17] 李法军．河北阳原姜家梁新石器时代人骨研究[D]．长春：吉林大学，2004

[18] 张燕，赵东月，刘化石，等．四川会理县猴子洞遗址2017 年出土人骨研究[J]．四川文物，2021， 6： 104-116

[19] 韩如月．陕西咸阳蒲家寨墓地出土人骨研究[D]．西安：西北大学，2022

[20] 李楠．“区域模型生命表”在古人口学研究中的应用[J]．人类学学报，2019， 38（1）： 98-106

[21] 宋先杰．基于生命表法的大汶口文化时期古人平均预期寿命初探[D]．济南：山东大学，2011

[22] 李法军．生物人类学（第二版）[M]．广州：中山大学出版社，2020， 456-457

[23] Angel JL. The bases of paleodemography[J]. American Journal of Physical Anthropology， 1969， 30（3）： 427-437

[24] Petersen W， Braidwood RJ， Dobyns HF， et al. A demographer's view of prehistoric demography （and comments and replies）[J].Current Anthropology， 1975， 16（2）： 227-245

[25] Frankenberg SR， Konigsberg LW. A brief history of paleodemography from Hooton to hazards analysis[A]. In： Buikstra JE， BeckLA （Eds）. Bioarchaeology： The Contextual Analysis of Human Remains[M]. London： Routledge， 2006， 227-261

[26] Wilson JJ. Life table analysis[A]. In： Varela SLL （Eds）. The Encyclopedia of Archaeological Sciences[M]. New York： John Wiley& Sons， 2018， 1-3

[27] 塞缪尔·普雷斯顿，帕特里克·霍伊维兰，米歇尔·吉略特．人口统计学：人口过程的测量与建模[M]．北京：社会科学文献出版社，2012， 15-16

[28] 郭未．人口学[M]．北京：社会科学文献出版社，2018， 254-255

[29] 翟振武．简略生命表中A 值的研究[J]．人口研究，1988， 3： 40-44

[30] 张羚广，蒋正华，林宝．人口信息分析技术[M]．北京：中国社会科学出版社，2006， 49

[31] 查瑞传．生命表[J]．人口研究，1981， 3： 55-61

[32] 马瀛通．数理统计分析人口学[M]．北京：中国人口出版社，2010， 414-415

[33] Sattenspiel L， Harpending H. Stable populations and skeletal age[J]. American Antiquity， 1983， 48（3）： 489-498

[34] Milner GR， Wood JW， Boldsen JL. Paleodemography： problems， progress， and potential[A]. In： Katzenberg MA， Grauer AL （Eds）.Biological Anthropology of the Human Skeleton[M]. Hoboken： Wiley-Blackwell， 2018， 593-633

[35] 查瑞传．静止人口和稳定人口[J]．人口研究，1981， 1： 44-49

[36] Johansson SR， Horowitz S. Estimating mortality in skeletal populations： influence of the growth rate on the interpretation of levelsand trends during the transition to agriculture[J]. American Journal of Physical Anthropology， 1986， 71（2）： 233-250

[37] McFadden C. The past， present and future of skeletal analysis in palaeodemography[J]. Philosophical Transactions of the RoyalSociety B， 2021， 376（1816）： 20190709

[38] Séguy I， Buchet L， Bringé A. Model life tables for pre-industrial populations： first application in palaeodemography[A]. In：Bocquet-Appel JP （Eds）. Recent Advances in Palaeodemography[M]. Dordrecht ： Springer， 2008， 83-117

[39] Chamberlain A. Archaeological demography[J]. Human biology， 2009， 81（3）： 275-286

[40] Wood JW， Milner GR， Harpending HC， et al. The osteological paradox： problems of inferring prehistoric health from skeletalsamples [and comments and reply][J]. Current anthropology， 1992， 33（4）： 343-370

[41] Lopez A. Problems in Stable Population Theory[M]. Office of Population Research， Princeton University， 1961， 66-68

[42] Bonneuil N. Turbulent dynamics in a XVIIth century population[J]. Mathematical Population Studies， 1990， 2（4）： 289-311

[43] Bonneuil N. Fitting to a distribution of deaths by age with application to paleodemography： The route closest to a stablepopulation[J]. Current Anthropology， 2005， 46（S5）： 29-45

[44] Page AE， French JC. Reconstructing prehistoric demography： What role for extant hunter-gatherers？[J]. EvolutionaryAnthropology： Issues， News， and Reviews， 2020， 29（6）： 332-345

[45] Carrier NH. A note on the estimation of mortality and other population characteristics given deaths by age[J]. Population Studies，1958， 12（2）： 149-163

[46] Howell N. Toward a uniformitarian theory of human paleodemography[J]. Journal of Human Evolution， 1976， 5（1）： 25-40

[47] French JC， Chamberlain AT. Demographic uniformitarianism： the theoretical basis of prehistoric demographic research and itscross-disciplinary challenges[J]. Philosophical Transactions of the Royal Society B， 2021， 376（1816）： 20190720

[48] Gage TB， Dewitte SN， Wood JW. Demography part 1： Mortality and migration[A]. In： Stinson S， Bogin B， O'Rourke DH （Eds）.Human Biology： An Evolutionary and Biocultural Perspective[M]. Chichester： John Wiley & Sons， 2012， 693-755

[49] Lovejoy CO， Meindl RS， Pryzbeck TR， et al. Paleodemography of the Libben site， Ottawa county， Ohio[J]. Science， 1977，198（4314）： 291-293

[50] Meindl RS， Mensforth RP， Lovejoy CO. The Libben site： A hunting， fishing， and gathering village from the eastern late woodlandsof North America. Analysis and implications for palaeodemography and human origins[A]. In： Bocquet-Appel JP （Eds）. RecentAdvances in Palaeodemography[M]. Dordrecht ： Springer， 2008， 259-275

[51] Bocquet-Appel JP. Paléodémographie： ce que nous apprend la Nubie soudanaise[J]. Annales. Histoire， Sciences Sociales， 1977， 32（1）： 54-69

[52] Lovejoy CO， Meindl RS， Mensforth RP， et al. Multifactorial determination of skeletal age at death： a method and blind tests of its accuracy[J]. American Journal of Physical Anthropology， 1985， 68（1）： 1-14

[53] Mensforth RP. Paleodemography of the Carlston Annis （Bt-5） late archaic skeletal population[J]. American Journal of PhysicalAnthropology， 1990， 82（1）： 81-99

[54] Bocquet-Appel JP， Bacro JN. Brief communication： Estimates of some demographic parameters in a neolithic rock-cut chamber（approximately 2000BC） using iterative techniques for aging and demographic estimators[J]. American Journal of PhysicalAnthropology， 1997， 102（4）： 569-575

[55] Howell N. Demography of the Dobe！ Kung[M]. New York： Academic Press， 1979

[56] Woods R. On the historical relationship between infant and adult mortality[J]. Population Studies， 1993， 47（2）： 195-219

[57] Wrigley EA， Davies RS， Oeppen JE， et al. English Population History from Family Reconstitution， 1580-1837[M]. Cambridge：Cambridge University Press， 1997

[58] Meindl RS， Russell KF. Recent advances in method and theory in paleodemography[J]. Annual review of Anthropology， 1998， 27： 375-399

[59] DeWitte SN. Paleodemography[A]. In： Trevathan W. The International Encyclopedia of Biological Anthropology[M]. Hoboken：Wiley-Blackwell， 2018， 1119-1126

[60] Coale AJ， Demeny P. Regional Model Life Tables and Stable Populations[M]. Princeton： Princeton University Press， 1966， 7

[61] Crews DE. Biological anthropology and human aging： some current directions in aging research[J]. Annual Review ofAnthropology， 1993， 22（1）： 395-423

[62] Bocquet-Appel JP， Masset C. Farewell to paleodemography[J]. Journal of Human Evolution， 1982， 11（4）： 321-333

[63] Nawrocki SP. The nature and sources of error in the estimation of age at death from the skeleton[A]. In： Latham KE， Finnegan M（Eds）. Age Estimation of the Human Skeleton[M]. Springfield： Charles C Thomas Publisher， 2010， 79-101

[64] Lovejoy CO， Meindl RS， Tague RG， et al. The senescent biology of the hominoid pelvis： its bearing on the pubic symphysis andauricular surface as age-at-death indicators in the human skeleton[J]. Rivista di Antropologia， 1995， 73： 31-49

[65] Ruengdit S， Case DT， Mahakkanukrauh P. Cranial suture closure as an age indicator： a review[J]. Forensic science international，2020， 307： 110-111

[66] Dudar JC， Pfeiffer S， Saunders SR. Evaluation of morphological and histological adult skeletal age-at-death estimation techniquesusing ribs[J]. Journal of Forensic Science， 1993， 38（3）： 677-685

[67] Howell N. Village composition implied by a paleodemographic life table： the Libben site[J]. American Journal of PhysicalAnthropology， 1982， 59（3）： 263-269

[68] Willey P， Mann B. The skeleton of an elderly woman from the Crow Creek site and its implications for paleodemography[J]. PlainsAnthropologist， 1986， 31（112）： 141-152

[69] Baker PT， Sanders WT. Demographic studies in anthropology[J]. Annual Review of Anthropology， 1972， 151-178

[70] Mcfadden C， Muir B， Oxenham MF. Determinants of infant mortality and representation in bioarchaeological samples： A review[J].American Journal of Biological Anthropology， 2022， 177（2）： 196-206

[71] Paine RR， Harpending HC. Assessing the reliability of paleodemographic fertility estimators using simulated skeletaldistributions[J]. American Journal of Physical Anthropology， 1996， 101（2）： 151-159

[72] Hoppa R， Saunders S. The MAD legacy： how meaningful is mean age-at-death in skeletal samples[J]. Human Evolution， 1998， 13（1）： 1-14

[73] Ubelaker DH. Weighting of age interval values in life table construction[J]. Anthropologie， 2001， 39（1）： 9-14

[74] Luy MA， Wittwer-Backofen U. The Halley band for paleodemographic mortality analysis[A]. In： Bocquet-Appel JP （Eds）. RecentAdvances in Palaeodemography[M]. Dordrecht： Springer， 2008， 119-141

[75] Getz SM. The use of transition analysis in skeletal age estimation[J]. Wiley Interdisciplinary Reviews： Forensic Science， 2020， 2（6）： e1378

[76] Horowitz S， Armelagos G， Wachter K. On generating birth rates from skeletal populations[J]. American Journal of PhysicalAnthropology， 1988， 76（2）： 189-196

[77] McFadden C， Oxenham MF. The D0-14/D ratio： A new paleodemographic index and equation for estimating total fertility rates[J].American Journal of Physical Anthropology， 2018， 165（3）： 471-479

[78] Wood JW， Holman DJ， OConnor KA， et al. Mortality models for paleodemography[A]. In： Hoppa RD， Vaupel JW （Eds）.Paleodemography： Age Distributions from Skeletal Samples[M]. Cambridge： Cambridge University Press， 2008， 129-168

[79] Boldsen JL， Milner GR， Ousley SD. Paleodemography： From archaeology and skeletal age estimation to life in the past[J].American Journal of Biological Anthropology， 2022， 178（S74）： 115-150

[80] Buikstra JE， DeWitte SN， Agarwal SC， et al. Twenty-first century bioarchaeology： Taking stock and moving forward[J]. AmericanJournal of Biological Anthropology， 2022， 178（S74）： 54-114

[81] Gage TB. Mathematical hazard models of mortality： an alternative to model life tables[J]. American Journal of PhysicalAnthropology， 1988， 76（4）： 429-441

[82] Gage TB， Dyke B. Parameterizing abridged mortality tables： The Siler three-component hazard model[J]. Human Biology， 1986， 275-291

[83] Wood JW， Holman DJ， Weiss KM， et al. Hazards models for human population biology[J]. American Journal of PhysicalAnthropology， 1992， 35（S15）： 43-87

[84] Siler W. Parameters of mortality in human populations with widely varying life spans[J]. Statistics in Medicine， 1983， 2（3）： 373-380

[85] Siler W. A competing-risk model for animal mortality[J]. Ecology， 1979， 60（4）： 750-757

[86] Castellares F， Patrício S， Lemonte AJ. On the Gompertz-Makeham law： A useful mortality model to deal with human mortality[J].Brazilian Journal of Probability and Statistics， 2022， 36（3）： 613-639

[87] Gurven M， Kaplan H. Longevity among hunter-gatherers： a cross-cultural examination[J]. Population and Development review，2007， 33（2）： 321-365

[88] Nagaoka T， Hirata K. Reconstruction of paleodemographic characteristics from skeletal age at death distributions： perspectivesfrom Hitotsubashi， Japan[J]. American Journal of Physical Anthropology， 2007， 134（3）： 301-311

[89] Dewitte SN. Modeling the second epidemiologic transition in London： Patterns of mortality and frailty during industrialization[J].Modern environments and human health： Revisiting the second epidemiologic transition， 2014， 35-53

[90] Redfern RC， DeWitte SN， Pearce J， et al. Urban–rural differences in R oman D orset， E ngland： A bioarchaeological perspective onR oman settlements[J]. American Journal of Physical Anthropology， 2015， 157（1）： 107-120

[91] Kieffer CL. Modeling， simulating， and comparing biased archaeological mortuary assemblages[J]. International Journal ofPopulation Studies， 2021， 7（2）： 80-92

[92] Betsinger TK， Dewitte S. Trends in mortality and biological stress in a medieval polish urban population[J]. International Journalof Paleopathology， 2017， 19： 24-36

[93] Boldsen JL. Leprosy and mortality in the Medieval Danish village of Tirup[J]. American Journal of Physical Anthropology， 2005，126（2）：159-168

[94] Walter BS. Paleodemographic and biochemical analysis of urbanization， famine， and mortality[D]. Columbia： University of SouthCarolina， 2017

[95] Walter BS， DeWitte SN. Urban and rural mortality and survival in Medieval England[J]. Annals of Human Biology， 2017， 44（4）： 338-348

[96] Kelmelis S， DeWitte SN. Urban and rural survivorship in pre-and post-Black Death Denmark[J]. Journal of ArchaeologicalScience： Reports， 2021， 38： 103089

[97] Zoeller GE， Drew BL， Schmidt CW， et al. A paleodemographic assessment of mortality and fertility rates during the seconddemographic transition in rural central Indiana[J]. American Journal of Human Biology， 2022， 34（1）： e23571

[98] French JC， Riris P， Fernandez-Lopez de Pablo J， et al. A manifesto for palaeodemography in the twenty-first century[J].Philosophical Transactions of the Royal Society B， 2021， 376（1816）： 20190707

[99] Buikstra JE， Konigsberg LW， Bullington J. Fertility and the development of agriculture in the prehistoric Midwest[J]. AmericanAntiquity， 1986， 51（3）： 528-546

[100] Lesnik JJ， Sams AJ. Using resampling statistics to test male interment bias： Applications for looted and commingled prehistoricremains in Peru and the reassessment of Neandertal burials[J]. PaleoAnthropology， 2014： 463-469

[101] Duering A. Modelling massacres. The agent-based modelling of catastrophic events using skeletal data from archaeologicalexcavations[J]. Anthropologischer Anzeiger， 2019， 76（3）： 217-221

[102] Konigsberg LW， Frankenberg SR. Paleodemography： “Not quite dead”[J]. Evolutionary Anthropology： Issues， News， andReviews， 1994， 3（3）： 92-105

[103] Bocquet-Appel JP. When the worlds population took off： the springboard of the Neolithic Demographic Transition[J]. Science，2011， 333（6042）： 560-561