截割间距对镐型截齿破岩特性影响的试验研究

刘滨 李雪峰

摘要：鎬型截齿是掘进机、采煤机等矿山机械上应用最广泛的截齿类型。在实际截割过程中，镐型截齿主要工作于多齿耦合截割工况下，截割间距是该工况下的重要参数。针对截割间距对破岩过程影响的研究未考虑干涉截割的弱化作用的问题，提出一种多齿耦合截割时截割力的计算方法。针对石灰岩、红砂岩和2种模拟岩样开展了全尺寸单齿截割试验，对比分析自由截割和干涉截割的破岩过程。试验采集了截割力数据并进行了降噪处理，同时收集了截割碎屑，分析了截割间距对截割载荷、截割碎屑粒度、截割能耗、截割沟槽的影响规律。试验结果表明：①截齿截割力随截割间距增加而增大，并逐渐接近自由截割状态，且干涉截割与自由截割条件下的截割力比值与截割间距/截割深度之间存在较好的线性关系，相关系数均大于0.95。说明干涉截割条件下截齿的截割载荷可利用自由截割载荷进行估算，进而得到了基于已有峰值截割力模型的干涉截割条件下的截割力估算方程。②分别采用碎屑粒度指数（CI）和截割比能耗（SE）评价截割试验的碎屑粒度分布和截割能耗。随截割间距增大，CI呈先增大后减小的趋势，而 SE呈先减小后增大的趋势。③当截割间距较小时，截割沟槽干涉显著，截割沟槽间残余岩脊较小，截割载荷较小，但由于截割沟槽干涉会产生较多细小碎屑，消耗较多能量，所以能耗升高；随着截割间距增大，残余岩脊增大，截割力增大，但由于已有截割沟槽对岩石的弱化作用且截割沟槽间干涉较少，形成的大块碎屑占比增大，所以截割能耗降低；随着截割间距进一步增大，截割沟槽间无干涉，且已有截割沟槽对岩石的弱化作用降低，截割力增大，碎屑粒度减小，截割能耗上升，截割状态逐渐趋近于自由截割。

关键词：螺旋滚筒；煤岩截割；镐型截齿；截割间距；干涉截割；自由截割；截割沟槽；截割深度中图分类号： TD421.5    文献标志码： A

Experimental study on the influence of cutting distance on the rock-breaking features of pick-shaped cutter

LIU Bin， LI Xuefeng

（College of Mechanical Engineering， Nanjing Vocational University of Industry Technology， Nanjing 210023， China）

Abstract： The pick-shaped cutter is the most widely used cutter type in mining machinery such as roadheader and coal mining machine. In the actual cutting process， the pick-shaped cutter mainly works under the multi-tooth coupling cutting condition. The cutting distance is an important parameter under this working condition. At present， research on the influence of cutting spacing on the rock-breaking process has not considered the weakening effect of interference cutting. A calculation method for cutting force during multi-tooth coupling cutting is proposed to solve the above problem. Full-size single-tooth cutting tests are carried out on limestone， red sandstone and two simulated rock samples， comparing and analyzing the rock-breaking processes of free cutting and interference cutting. The experiment collects cutting force data and conducts noise reduction processing and collects cutting debris to analyze the impact law of cutting spacing on cutting load， cutting debriscoarseness， cutting energy consumption， and cutting grooves. The experimental results show the following points.① The cutting force of the cutter increases with the increase of cutting distance and gradually approaches the free cutting state. Moreover， there is a good linear relationship between the cutting force ratio under interference cutting and free cutting conditions and the cutting distance/cutting depth. The correlation coefficients are greater than 0.95. The cutting load of the cutter under interference cutting conditions can be estimated using the free cutting load. The cutting force estimation equation under interference cutting conditions based on the existing peak cutting force model is obtained.② The coarseness index （CI） and specific energy （SE） are used respectively to evaluate the particle size distribution and cutting energy consumption of the cutting experiment. As the cutting distance increases， CI shows a trend of first increasing and then decreasing. SE shows a trend of first decreasing and then increasing.③ When the cutting distance is small， the interference between the cutting grooves is significant， the residual rock ridges between the cutting grooves are small， and the cutting load is small. However， due to the interference between the cutting grooves， more small debris is generated. It consumes more energy and increases energy consumption. As the cutting distance increases， the residual rock ridge increases， and the cutting force increases. However， due to the weakening effect of existing cutting grooves on the rock and less interference between cutting grooves， the proportion of large debris formed increases， and the cutting energy consumption decreases. As the cutting distance further increases， there is no interference between the cutting grooves. The weakening effect of the existing cutting grooves on the rock decreases. The cutting force increases， the coarseness decreases， and the cutting energy consumption increases. The cutting state gradually approaches free cutting.

Key words： spiral drum; coal rock cutting; pick-shaped cutter; cutting distance; interference cutting; free cutting; cutting grooves; cutting depth

0 引言

采掘装备的截割能效问题是采矿行业研究的永恒课题，而截齿是截割机具上直接接触、破碎岩石的关键零件，截齿破岩过程是采掘装备最主要的能耗环节。镐型截齿具有结构简单、自磨刃等特点，成为应用最广泛的截齿类型。影响镐型截齿破岩效率的主要因素包括截齿安装参数（如截割间距、截割冲击角、歪斜角）、截齿形状参数（如齿尖锥角、合金头直径、齿身锥角）、采掘装备工况参数（如截割速度、截割深度、岩石特性、地应力）等[1-6]。其中截割间距决定了多齿耦合截割的干涉状态，是影响截齿截割效率、截割碎屑粒度、截割载荷及截齿磨损的重要因素之一。

为便于表述，本文将单齿截割和不同间距下的截割分别称为自由截割和干涉截割。针对截割间距对破岩过程的影响，学者们进行了大量研究。文献[7]通过实验对比研究了刀型截齿、镐型截齿和刀盘的截割效率，分析了截割比能耗和碎屑粒度与截割间距之间的关系。文献[8]通过单齿截割实验分析了截齿破岩机制及截割间距对破岩效果的影响。文献[9]在截割实验数据的基础上，通过统计学分析研究了截割载荷与截割间距和截割厚度之间的关系。文献[10]采用数值模拟方法研究了截割间距对截割载荷的影响规律，为优化截割间距与截割深度比值提供依据。在截割理论研究方面，学者们基于不同的力学准则提出了自由截割条件下截齿破岩机理和截割力计算模型。基于最大拉应力准则提出的镐型截齿截割力模型[11]及其改进模型[12-14]得到广泛认可。文献[15]基于莫尔?库伦准则提出了刀型截齿的截割模型。文献[16]基于断裂力学分析了截割破碎过程中层理、节理的失稳破裂机理，建立了刀型截齿截割力模型。文献[17]认为截齿截割峰值力出现在裂纹起裂阶段，基于格里菲斯断裂理论建立了镐型截齿截割峰值力模型。而在干涉截割条件下，已有截割沟槽不仅改变了齿尖受力状态，且对岩石起到不同程度的弱化作用，其截割力无法直接采用已有理论模型进行估算。滚筒扭矩是多齿耦合截割载荷的叠加结果，而已有滚筒载荷计算模型主要基于单齿截割力理论模型计算单齿截割力后进行简单叠加[18-19]，而没有考虑截割间距对多齿耦合截割过程中截割力的影响。

针对已有截割理论未考虑干涉截割的弱化作用的问题，本文开展了截割间距对截齿载荷影响规律的试验研究，提出一种多齿耦合截割时截割力的计算方法。通过全尺寸岩石线性截割试验对比分析自由截割和干涉截割破岩过程，研究2种截割工况下截割力的统计关系，建立干涉截割条件下截割力的计算方法，基于已有截割力理论模型得到不同截割间距下的单齿截割力，进而得到考虑多齿耦合的滚筒载荷计算方法。

1 截割试验装置及岩石试样制备

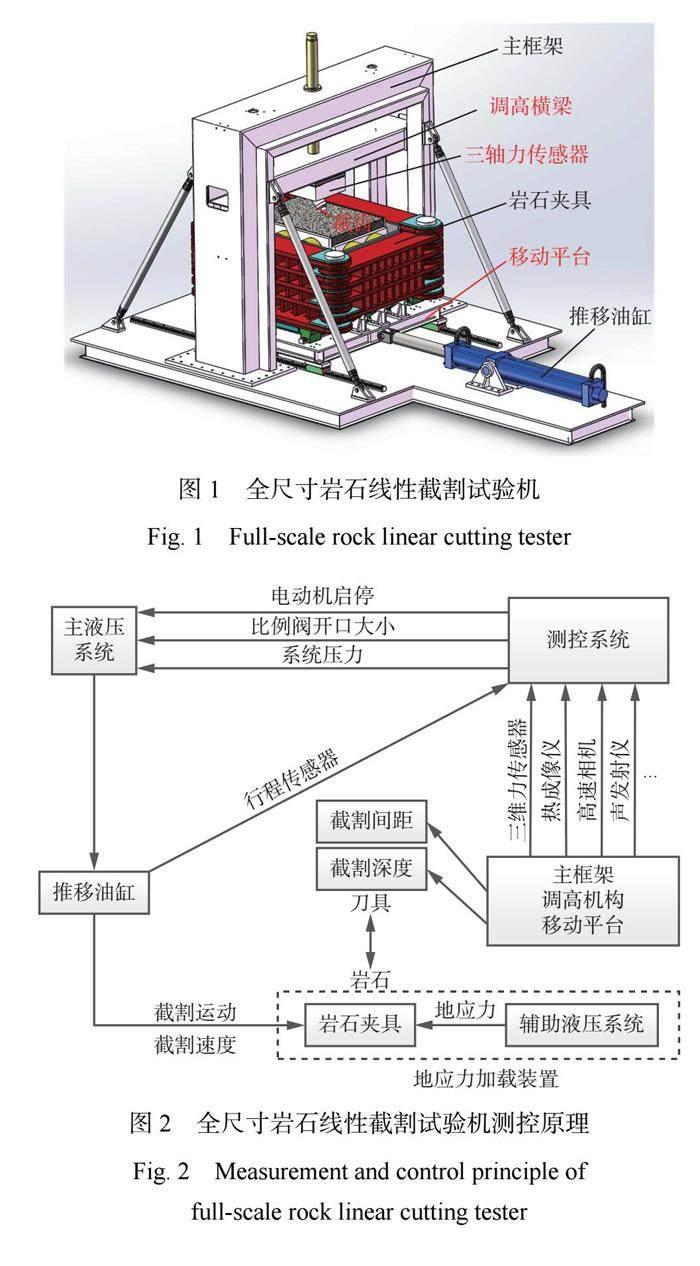
为降低岩石边界对截割过程的影响，采用全尺寸岩石线性截割试验机（图1）开展煤岩截割试验，该试验机由主框架、推移油缸、岩石夹具、测控系统、液压系统等组成。其测控原理如图2所示，主框架的调高机构和移动平台实现截齿截割深度和截割间距的调节，推移油缸实现截割运动，测控系统实现截割力和截割速度的采集。该试验机能够夹装的最大岩石尺寸为1 m×0.7 m×0.7 m，装配有三轴力传感器采集截齿三向力（图3），其中 FX 为截割力，FY 为侧向力，FZ 为法向力，三轴量程均为±500 kN，截割速度调节范围为0～0.3 m/s。针对截割间距的试验方案如图4所示，其中，d 为截割深度，s 为截割间距。首先单截齿截割岩石表面形成沟槽，即先行截齿，而后截齿偏移固定间距后截割岩石，即后行截齿，从而通过单齿截割试验模拟不同截割间距的破岩过程，截割间距调节范围为0～300 mm。

本文截割试验用到的岩石样品有石灰岩、红砂岩和2种模拟岩样，岩石试样尺寸均为1 m×0.5 m×0.5 m，如图5所示。通过岩石单轴压缩试验和巴西劈裂试验测得岩样的单轴抗压强度、抗拉强度、弹性模量和泊松比，测试结果见表1，可看出表明所选岩样的单轴抗压强度为13.3～116.4 MPa。

本文截割试验所用 U135?25镐形截齿，试验设置截齿冲击角为50°， 截割速度为50 mm/s，截齿齿尖锥角为90°。截割间距 s 和截割深度 d 为试验变量，参数设置见表2。

2 截割力数据处理

受到试验环境噪声、传感器和数据采集卡性能等因素的影响，实验过程中采集到的截割力数据包含较多高频噪声成分，无法直接用于截割力数据分析。降噪前截割三向力曲线如图6所示，可看出噪声波动较明显，覆盖了截割力曲线特征，尤其对 Y 方向截割力的影响最为显著。因此，在截割力分析之前须对截割数据进行降噪处理。

采用经验模态分解（Empirical Mode Decomposition，EMD）对截割载荷数据进行降噪处理。 EMD 方法将原始信号按照频率成分分解为多个本征模态函数（Intrinsic Mode Function，IMF），理想状态下每个 IMF具有单一频率，能够反映信号在频域中的局部特征[20]。基于 EMD 分解结果，剔除噪声成分后进行信号重构，达到降噪的目的。 EMD 分解的具体步骤如下：

1）获得原始信号 z（t）的所有极大值和极小值点，记为 x（t），t 为时间。

2）采用插值法得到极值点，形成上包络线emax（t）和下包络线emin（t）。

3）计算原始信号与上、下包絡线均值 a（t）的差值 h（t），即

4）如果 h（t）的极值点数量和过零点数量相等或相差1，则 h（t）为一个 IMF 分量。否则，将 h（t）作为原始信号重复步骤1）—步骤4），当差值分量满足上述条件时得到 IMF 分量，并标记该分量为 y（t）。

5）将原始信号 z（t）与 y（t）的差值 z1（t）作为下一循环的原始信号进行分解，直到循环次数满足要求，得到残余分量 r（t）。

将原始信号分解成 N 个 IMF 分量和1个残余分量。截割力 FX 的分解结果如图7所示，该数据包含13个 IMF 分量和1个残余分量。可看出 IMF1? IMF5为高频噪声成分，在信号重构时去除噪声成分从而实现降噪。从降噪后的截割三向力曲线（图8）能够更清晰地看出截割力曲线的波动特性，其中 X 方向截割力波动较剧烈，且波谷接近0，这是由于截割过程中随碎屑崩落，截齿在截割方向上瞬间卸载；Y 方向截割力为截齿的侧向力，围绕0点波动； Z 方向截割力波动特性与 X 方向相近，但波动幅度较小，这是由于截割过程中齿尖在竖直方向始终与岩石接触。

3 试验结果与分析

根据截割间距及截割深度参数设置开展了一系列全尺寸截割试验，试验采集了截割力数据并完成降噪处理，同时收集截割碎屑，分析截割间距对截割载荷、截割碎屑粒度、截割能耗、截割沟槽的影响规律。

3.1 截割间距对截割载荷的影响

以模拟岩样 II（d=15 mm）为例，不同截割间距条件下截割三向力的均值见表3，截割载荷均值随截割间距的变化如图9所示。可看出截割力 FX 和法向力 FZ 的均值随截割间距的增加而增大。由于已有截割沟槽降低了截割沟槽两侧岩石表面的强度，从而降低了截齿截割载荷，但随着截割间距增大，截割沟槽间的干涉效果减弱，截割载荷增大，截割状态逐渐趋近于自由截割。而侧向力 FY 均为负值且绝对值随截割间距增加而减小。因为在干涉截割条件下，已有截割沟槽降低了齿尖一侧的载荷，且随着截割沟槽干涉效果的减弱，齿尖受力趋于对称，侧向力 FY 趨于0。

为进一步得到干涉截割条件下截割力的估算方法，分析了干涉截割和自由截割条件下截割载荷均值的比值fr随截割间距与截割深度比值 s/d 的变化关系，结果如图10所示。可看出 X 方向和 Z 方向的fr均与 s/d 之间存在较好的线性关系，相关系数 R2均大于0.95。因此，利用自由截割条件下截割载荷估算干涉截割条件下的截割载荷是可行的。

为进一步建立可靠的干涉截割与自由截割的截割力关系，对不同岩样的截割试验结果进行了统计分析，见表4。fr随 s/d 的变化趋势如图11所示，可看出两者具有较好的线性关系。

基于上述实验数据，采用线性回归分析建立干涉截割条件下单齿截割力均值估算方程，其相关系数为 R2=0.674。通过置信水平为95%的方差分析，得到截割峰值力 P 为0，说明该线性回归关系具有较高的可信度。已有研究结果表明[21]，自由截割工况状态下的截齿截割力均值与峰值力存在线性关系。因此可基于已有截齿截割峰值力理论模型[11-17]得到干涉截割条件下的截割力，进一步得到考虑多齿耦合截割影响的滚筒截割扭矩的理论计算方法。

式中：F1为干涉截割工况状态下的截割力均值，N； g 为截割间距影响系数；F0为自由截割工况状态下的截割力均值，N；a 为截割力均值与峰值系数， a=0.45[21]；M 为滚筒扭矩，N·m；i为参与截割的截齿编号；D 为滚筒直径， m。

3.2 截割间距对碎屑粒度和比能耗的影响

为进一步分析截割间距对截齿截割性能的影响，本文选用截割比能耗（Specific Energy， SE）和碎屑粒度指数（Coarseness Index， CI）2个定量评价指标分别对截割能耗和碎屑粒度分布进行评价。其中，SE 是指破碎单位体积岩石所消耗的能量[5]。CI 是碎屑粒度筛分后各等级质量百分比的累计值[7]， CI 值越大，说明大块碎屑的比例越高，可用于评价截割碎屑粒度分布。

式中：E为截割比能耗；Fˊ为平均截割力；L 为截割距离；m 为截割碎屑质量；ρ为岩样密度。

以截割模拟岩样 II（d=15 mm）为例，试验过程收集了不同截割间距时的碎屑，对其进行称重和粒度筛分，如图12所示。不同截割工况下计算得到的 CI 和 SE 汇总见表5。可看出当截割间距为20 mm 时，CI 值最小且 SE 最大，是包括自由截割在内的最差截割参数，说明截割间距过小时更多的能量被用于研磨而产生细小碎屑，导致截割能耗增大。

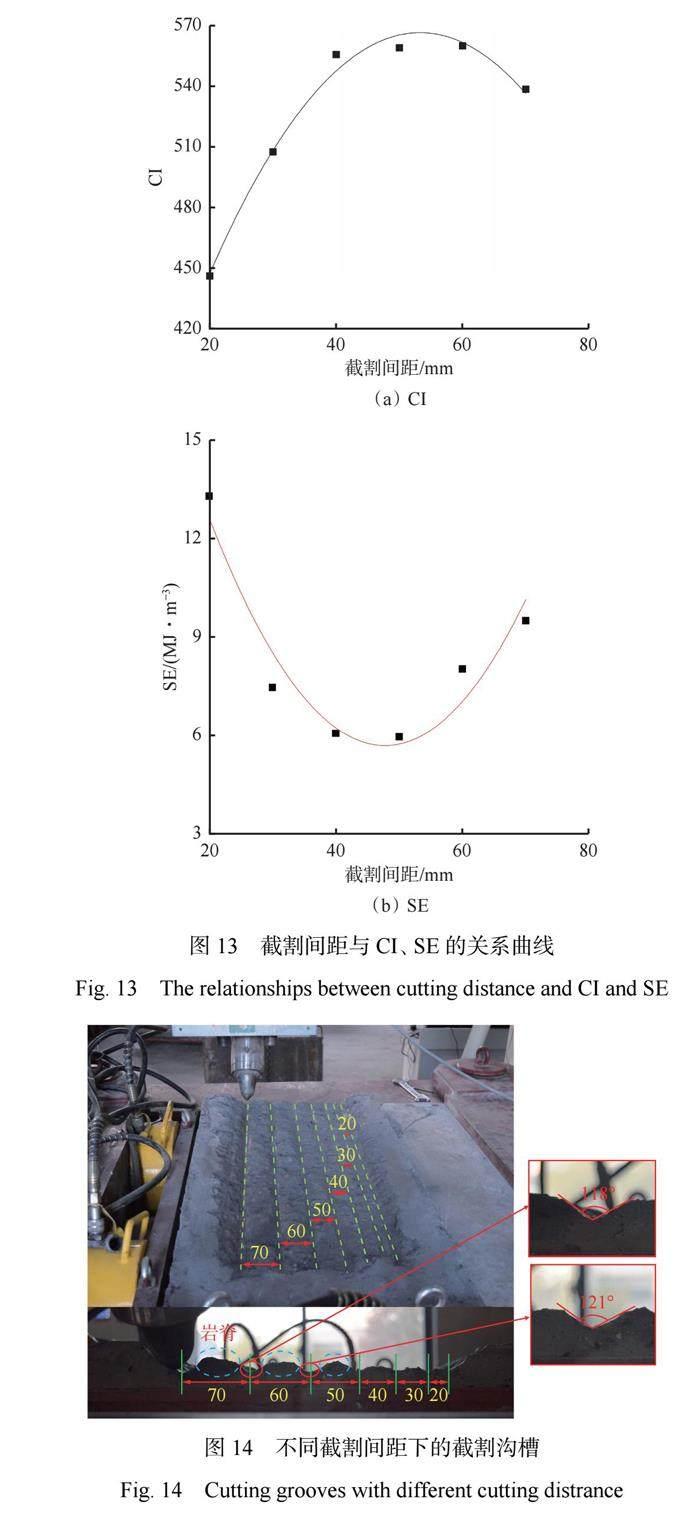
CI 和 SE 随截割间距的变化曲线如图13所示。可看出随截割间距增大，CI 呈先增大后减小的趋势，而 SE 呈相反的变化规律。说明随着截割间距增大，大块碎屑占比增多，截割能耗降低，且存在最优的截割间距约为50 mm；而随着截割间距进一步增大，截割性能下降并趋于稳定，截割状态趋于自由截割。

3.3 截割间距对截割沟槽的影响

不同截割间距下截割模拟岩样 II（d=15 mm）的截割沟槽如图14所示。可看出，随着截割间距增大，截割沟槽截面间干涉减少，而残余的岩脊增多。

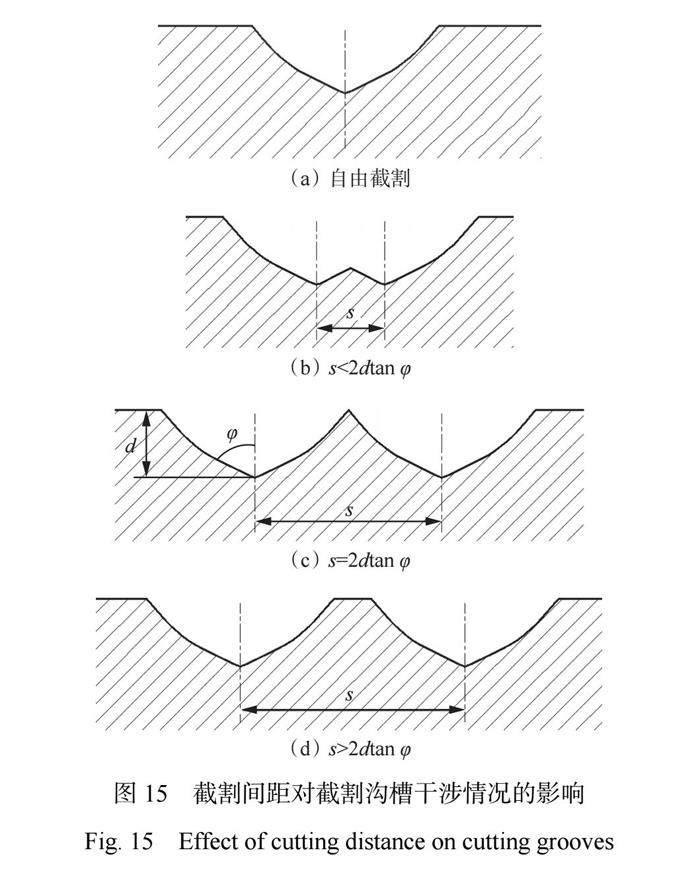
截割间距对截割沟槽干涉情况如图15所示。当截割间距较小时，截割沟槽干涉显著，截割沟槽间残余岩脊较小，截割载荷较小，但由于截割沟槽干涉会产生较多细小碎屑，消耗较多能量，所以能耗升高；随着截割间距增大，残余岩脊增大，截割力增大，但由于已有截割沟槽对岩石的弱化作用且截割沟槽间干涉较少，形成的大块碎屑占比增大，所以截割能耗降低；随着截割间距进一步增大，截割沟槽间无干涉，且已有截割沟槽对岩石的弱化作用降低，截割力增大，碎屑粒度减小，截割能耗上升，截割状态逐渐趋近于自由截割。

因此截割沟槽恰不干涉时为最优截割条件，该条件下最优截割间距为

式中φ为截割崩落角。

在模拟岩样 II 的干涉截割试验条件下（d=15 mm），截割崩落角约为60°， 最优截割间距约为51.9 mm，与试验结果（50 mm）较接近。

4 结论

通过全尺寸岩石线性截割试验，分析了截割间距对截割载荷、截割碎屑粒度、截割比能耗及截割沟槽的影响规律。

1）截齿截割力随截割间距增加而增大，并逐渐接近自由截割状态。干涉截割与自由截割条件下的截割载荷均值比值与 s/d 之间存在较好的线性关系，得到了基于已有峰值截割力模型的干涉截割时截割力的估算方程。

2）采用 CI 和 SE 分别评价截割试验的碎屑粒度分布和截割能耗，随截割间距增大，CI 呈先增大后减小的趋势，而 SE 呈先减小后增大的趋势。

3）当截割间距较小时，截割沟槽干涉显著，截割沟槽间残余岩脊较小，截割载荷较小，但由于截割沟槽干涉会产生较多细小碎屑，消耗较多能量，所以能耗升高；随着截割间距增大，残余岩脊增大，截割力增大，但由于已有截割沟槽对岩石的弱化作用且截割沟槽间干涉较少，形成的大块碎屑占比增大，所以截割能耗降低；随着截割间距进一步增大，截割沟槽间无干涉，且已有截割沟槽对岩石的弱化作用降低，截割力增大，碎屑粒度减小，截割能耗上升，截割状态逐渐趋近于自由截割。

参考文献（References）：

[1] WANG Xiang，WANG Qingfeng，LIANG Yunpei，et al. Dominant cutting parameters affecting the specific energy of selected sandstones when using conical picks and the development of empirical prediction models[J]. Rock Mechanics and Rock Engineering，2018，51（10）：3111-3128.

[2] LIU Songyong，CUI Xinxia，DU Changlong，et al. Method to determine installing angle of conical point attack pick[J]. Journal of Central South University of Technology，2011，18（6）：1994-2000.

[3] HEKIMOGLU O Z. Suggested methods for optimum rotativemotion of point attack type drag tools in terms of skew angles[J]. International Journal of Mining Reclamation & Environment，2019（1）：1-19.

[4] BAO Ronghao，ZHANG Liangchi，YAO Qingyu，et al. Estimating the peak indentation force of the edge chipping of rocks using single point-attack pick[J]. Rock Mechanics and Rock Engineering，2011，44（3）：339-347.

[5] BALCI C，TUMAC D. Investigation into the effects of different rocks on rock cuttability by a V-type disc cutter [J]. Tunnelling  and  Underground  Space Technology，2012，30：183-193.

[6] 劉春生，宋杨.不同楔入角的镐齿破岩截割力模型与仿真[J].黑龙江科技学院学报，2012，22（3）：277-281，205.

LIU Chunsheng， SONG Yang. Development and simulation of cutting force model on conical pick cutting rock at different wedge angles[J]. Journal of Heilongjiang Institute of Science and Technology，2012，22（3）：277-281，205.

[7] TUNCDEMIR H，BILGIN N，COPUR H，et al. Control of rock cutting efficiency by muck size[J]. International Journal of Rock Mechanics and Mining Sciences，2008，45（2）：278-288.

[8] 张倩倩，韩振南，张梦奇，等.截齿破岩机制及截线间距优化试验研究[J].岩土力学，2016，37（8）：2172-2179，2186.

ZHANG Qianqian，HAN Zhennan，ZHANG Mengqi，et al. Experimental study of breakage mechanisms of rock induced by a pick and associated cutter spacing optimization[J]. Rock and Soil Mechanics，2016，37（8）：2172-2179，2186.

[9] 梁运培，王想，王清峰.截割厚度与截线距对镐型截齿破岩力学参数的影响[J].振动与冲击，2018，37（3）：27-33.

LIANG Yunpei， WANG Xiang， WANG Qingfeng. Effects of cut depth and cut spacing on tool forces acting on a conical pick in rock cutting[J]. Journal of Vibration and Shock，2018，37（3）：27-33.

[10] 逯振国，李长江，王洪斌，等.截线间距与截齿截深的比值对截齿截割力的影响[J].煤炭技术，2022，41（2）：203-205.

LU Zhenguo，LI Changjiang，WANG Hongbin，et al. Effect of ratio of intersecting distance to cutting depth of pick on cutting force of pick[J]. Coal Technology，2022，41（2）：203-205.

[11] EVANS I. A theory of the picks cutting force for point- attack picks[J]. International Journal of Mining Engineering，1984，2（1）：63-71.

[12] GOKTAN R M， GUNNES N. A semi-empirical approach to cutting force prediction for point-attack picks[J]. South African Institute of Mining & Metallurgy，2005，105（2）：257-263.

[13] 王立平，蔣斌松，张翼，等.基于Evans截割模型的镐型截齿峰值截割力的计算[J].煤炭学报，2016，41（9）：2367-2372.

WANG Liping，JIANG Binsong，ZHANG Yi，et al.Calculation of peak cutting force of conical picks based on Evans' cutting model[J]. Journal of China Coal Society，2016，41（9）：2367-2372.

[14] 王立平，蒋斌松，张强.镐型截齿截槽非对称的峰值截割力计算[J].煤炭学报，2016，41（11）：2876-2882.

WANG Liping， JIANG Binsong， ZHANG Qiang. Calculation of peak cutting force of conical picks under conditions of dissymmetrical slotting[J]. Journal of China Coal Society，2016，41（11）：2876-2882.

[15] NISHIMATSU Y. The mechanics of rock cutting[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1972，9（2）：261-270.

[16] 牛东民.煤炭切削力学模型的研究[J].煤炭学报，1994，19（5）：526-530.

NIU Dongmin. Mechanical model of coal cutting[J]. Journal of China Coal Society，1994，19（5）：526-530.

[17] LI Xuefeng，WANG Shibo，GE Shirong，et al. A theoretical model for estimating the peak cutting force of conical picks[J]. Experimental Mechanics，2018，58（5）：709-720.

[18] 张强，张晓宇.不同卸荷工况下采煤机滚筒截割性能研究[J].河南理工大学学报（自然科学版），2022，41（1）：91-99，158.

ZHANG Qiang，ZHANG Xiaoyu. Research on cutting performance of shearer drum under different coal unloading condition[J]. Journal of Henan Polytechnic University（Natural Science），2022，41（1）：91-99，158.

[19] 麻晓红，于信伟，芦玉梅，等.复杂煤层采煤机滚筒载荷的数值模拟[J].黑龙江科技学院学报，2012，22（1）：42-46.

MA Xiaohong，YU Xinwei，LU Yumei，et al. Numerical simulation of shearer drum loads on complex coal seam [J]. Journal of Heilongjiang Institute of Science and Technology，2012，22（1）：42-46.

[20] YASER D，MASOUD S，VAHID C. Empirical mode decomposition and fourier analysis of caspian sea level's time series[J]. Ocean Engineering，2022，252（15）：1-10.

[21] BILGIN N， DEMIRCIN M A， COPUR H， et al. Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results[J]. International Journal of Rock Mechanics & Mining Sciences，2006，43（1）：139-156.