图论模型与算法在航天器下行数据故障诊断知识循环依赖缺陷检测中的应用

王 蕊 沈 星* 吴 伟 潘顺良

(1.南京航空航天大学航空学院, 南京 210016; 2.北京东方计量测试研究所, 北京 100094;3.北京空间飞行器总体设计部, 北京 100094)

1 引言

为确认在轨航天器的运行状态,保障飞行任务的正常开展,地面飞控人员需要实时监测航天器下行的遥测参数,并对其正确性进行诊断。随着航天器构造越来越复杂,下行遥测速率也越来越高。得益于中国第二代中继卫星天地测控通信系统的建设,目前天和核心舱的下行遥测速率已经达到了1.2 Gbps[1],较天舟系列货运飞船提升了1 个数量级[2],较神舟系列载人飞船提升约3 个数量级[3]。中国空间站构造复杂,并常驻航天员,其下行遥测参数的故障诊断不能简单地依靠若干门限,必须考虑各遥测参数以及上行遥控指令之间的依赖关系。

中国空间站等航天器从地面电性能测试开始就配套故障诊断系统[4],并最终在轨应用。航天器下行数据故障诊断系统属于专家系统[5-7]的一种,其核心在于专家知识库和推理引擎[8-9]。故障诊断推理引擎根据存在于知识库中的诊断知识,依据下行遥测参数和上行遥控指令,得出各遥测参数是否正常的结论,并发布给地面飞控人员。对于专家系统而言,知识获取是制约其应用的瓶颈问题[10]。虽然研究人员针对航天器下行数据故障诊断系统录入了大量的诊断知识,但其中依然存在缺陷的诊断知识,其中较为典型的一类知识缺陷是循环依赖,比如遥测参数A 的诊断知识依赖于遥测参数B,而遥测参数B 的诊断知识又和遥测参数A 相关。

图论[11-12]是应用数学的重要分支,从经典的哥尼斯堡七桥问题[13]、哈密顿圈问题[14]等,到现代的机器学习算法[15-18],图论都发挥了重要的作用。本文将遥测参数诊断知识中蕴藏的依赖关系抽象为有向图中的顶点和有向边,把诊断知识中的循环依赖检测问题抽象为有向图中的环搜索问题,应用经典拓扑排序算法、Kosaraju 算法[19]、Tarjan 算法[19]及本文提出的改进Tarjan 算法开展诊断知识的缺陷检测。

2 诊断知识分析

2.1 故障诊断知识库

为实现航天器下行数据的故障诊断,中国空间站等航天器采用了基于脚本的故障诊断系统。对于每个遥测参数,都可以录入一段诊断脚本,描述遥测参数所属设备或子系统的运行状态以及切换过程,并明确该遥测参数在不同状态下的值域判断逻辑,如图1 所示。

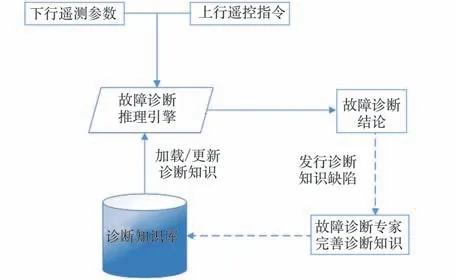
图1 航天器下行数据故障诊断系统示意图Fig.1 Schematic diagram of spacecraft downlink data fault diagnosis system

图2 是其中一个典型的诊断知识示例,描述了某电压量遥测参数A001 的诊断知识。其状态切换与SBKJ、SBGJ、QBF、QZF 等上行指令相关,而其值域则与某电流量遥测参数A002 相关,即遥测参数A001 的诊断知识脚本中描述了如何根据SBKJ、SBGJ、QBF、QZF 等上行指令确定当前参数所属设备的运行状态,再根据不同的状态得出正常值域的范围(所述值域与遥测参数A002 相关)。

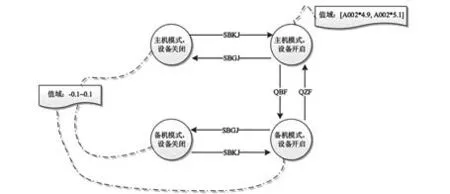
图2 遥测参数A001 的诊断知识示意图Fig.2 Schematic diagram of diagnostic knowledge of the telemetry data A001

由图2 可知,遥测参数A001 的诊断知识脚本中出现了相关指令和遥测参数A002。由于对所有的下行遥测参数均可以书写对应的故障诊断知识脚本,因此诊断知识中存在大量的不同下行遥测参数间的依赖关系。

2.2 循环依赖缺陷

在图2 所示遥测参数A001 的诊断知识中,其值域与参数A002 相关。若参数A002 的诊断知识如图3 所示,即参数A002 的状态切换过程与遥测参数A001 一致,其值域与参数A001 相关。由于参数A001 的值域也与参数A002 相关,这样就构成了一组循环依赖的诊断知识。显然出现循环依赖的参数A001 的诊断知识和参数A002的诊断知识是不完备的,因为若在设备开启且主机模式下这2 个遥测参数同时异常,但其遥测值依然满足大于4.9 且小于5.1 的比值关系,则故障诊断系统并不会诊断出异常。

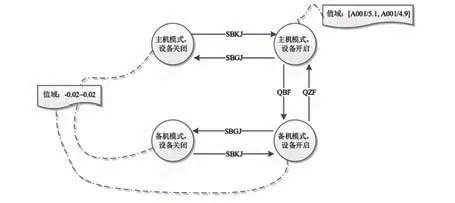
图3 遥测参数A002 的诊断知识示意图Fig.3 Schematic diagram of diagnostic knowledge of the telemetry data A002

即使对遥测参数A002 的诊断知识按图4 所示进行加强改进,即当参数A002 遥测值＜2 时,可以诊断出异常。但通过分析可知,其与参数A001之间的比值关系判断是冗余的,因为在参数A001的诊断知识中已经进行了该比值关系的判断。

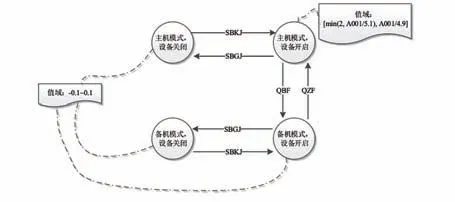
图4 改进后的遥测参数A002 诊断知识示意图Fig.4 Schematic diagram of improved diagnostic knowledge of the telemetry data A002

因此,若不同遥测参数的诊断知识中出现了循环依赖,一般而言意味着出现如下诊断知识缺陷:①故障诊断知识中可能存在不完备的表述;②故障诊断知识中可能存在冗余。

3 有向图模型及经典图算法

3.1 有向图模型构建

有向图D是指一个二元组(V(D),E(D)),其中V(D)表示顶点的集合,E(D)表示有向边集合;在有向图D中,E(D)中的每一个元素(即1 个有向边)对应于V(D)中的1 对有序元素(即2 个顶点)e=(x,y),其中x为1 个有向边的起点,y为这个有向边的终点;此外,用顶点出度表示起点为该顶点的有向边的数量,用顶点入度表示终点为该顶点的有向边的数量[20]。本文所述的有向图D不考虑2 个顶点之间存在多个有向边的情况,即有向图D为有向简单图。

当至少存在1 条路径可以由顶点xs到顶点xe,则称顶点xs至顶点xe可达。若有向图D中存在2 个顶点相互可达,则称有向图D中存在环。而若一个有向图D中的任意2 个顶点相互可达,则称有向图D是强连通(Strongly Connected);有向图D的极大强连通子图称为有向图D的强连通分量(Strongly Connected Components, SCC)。

针对本文所述航天器下行数据故障诊断系统中的诊断知识库,构建有向图Df= (Vf(D),Ef(D)),其中Vf(D)中的每个顶点对应1 个独立的遥测参数,而Ef(D)中的每一个有向边则表示其起点对应遥测参数的诊断知识与该有向边终点对应的遥测参数相关。

至此,遥测参数故障诊断知识中的循环依赖检测问题,就可抽象为有向图Df中的环搜索问题。对于本文构建的有向图Df,所有故障诊断知识中的循环依赖都对应于有向图Df中的环,且这些环都存在于有向图Df的SCC 中。

3.2 经典算法

3.2.1 拓扑排序算法

当拓扑排序算法[21]应用于诊断知识的循环依赖检测问题时,其运算步骤如下:

1)根据Vf(D)和Ef(D),统计出Df中所有顶点的入度,记录在列表List(Vf(D))中,此列表的元素个数为Vf(D)中的顶点个数,且每个元素中有对应顶点的入度信息。

2)扫描List(Vf(D))中所有入度为0 的元素,对于每个入度为0 的元素l,找到其对应的顶点x,并根据Ef(D)找出所有起点为x的有向边e,将所有e指向的终点对应的List(Vf(D))中元素的入度减去1;从List(Vf(D))中删除元素l。

3)反复执行步骤2,若列表List(Vf(D))已空,或者执行步骤2 后的列表List(Vf(D))与执行前相同,则执行步骤4。

4)若列表List(Vf(D))为空,则诊断知识中不存在循环依赖;否则List(Vf(D))中的每个元素所对应的遥测参数都处于循环依赖中。

上述拓扑排序检测算法通过执行1 次广度优先搜索,即可得出诊断知识中是否存在循环依赖的结论,其算法的时间复杂度为O(V+E),其中V代表Vf(D)中的顶点数目,而E代表Ef(D)中的有向边数目。

3.2.2 Kosaraju 算法

Kosaraju 算法[22]通过正反2 次深度优先搜索过程确定有向图中的SCC,也可以用于诊断知识的循环依赖检测,运算步骤如下:

1)对有向图Df中的所有顶点Vf(D),根据Ef(D)以后序深度优先搜索方式进行遍历入栈(栈Stack),所述后序深度优先是指先递归访问起点为当前顶点的有向边指向的终点,再入栈当前顶点;记录每个顶点的入栈时间。

2)将Ef(D)中的每个有向边反序,得到反序有向图D′f=(Vf(D),E′f(D))。

3)将Stack 中栈顶的顶点出栈,若该顶点已被步骤3 处理过,则执行步骤4;若该顶点未被步骤3 处理过,则由该顶点在反序有向图D′f中对应的顶点开始,根据E′f(D)进行深度优先搜索,记录由该顶点能够遍历到的所有顶点,这些顶点就构成了有向图Df的一个SCC,并标记这些顶点已被步骤3 处理过。

4)若Stack 已空,则算法结束;否则,继续步骤3。

Kosaraju 算法通过执行2 次深度优先搜索,可以得出有向图Df中的所有SCC,其算法的时间复杂度也为O(V+E)。

3.2.3 Tarjan 算法

Tarjan 算法[23]可以仅通过1 次深度优先搜索过程就确定有向图中的SCC,从而实现诊断知识的循环依赖检测。与Kosaraju 算法类似,Tarjan算法对图Df中的所有顶点Vf(D),根据Ef(D)以先序深度优先搜索方式进行遍历入栈,所述先序深度优先是指先访问当前顶点,再递归访问起点为当前顶点的有向边指向的终点,每次访问时执行如下步骤:

1)访问顶点时首先记录1 个该顶点的入栈时间,并初始化另一个称为可达最小入栈时间的值为同一时间;在Ef(D)中找出所有以该顶点为起点的有向边,对于每个有向边(x,y)执行步骤2;随后判断,若该顶点的入栈时间与可达最小入栈时间相同,则执行步骤3。

2)若y对应的顶点尚未入栈,则对y执行步骤1,并将x的可达最小入栈时间更新为x的可达最小入栈时间和y的可达最小入栈时间中的较小值;若y对应的顶点已入栈,则将x的可达最小入栈时间更新为x的可达最小入栈时间和y的入栈时间中的较小值。

3)执行出栈操作,直至步骤1 的当前访问顶点出栈,这些顶点构成有向图Df的1 个SCC。

Tarjan 算法仅通过1 次深度优先搜索,即可得出有向图Df的中的所有SCC,其算法的时间复杂度也为O(V+E)。

3.3 改进算法

引入图论模型后,可以应用上述拓扑排序、Kosaraju、Tarjan 等经典算法来检测故障诊断知识中的循环依赖缺陷,但考虑到航天器下行数据故障诊断系统的诊断知识会经常迭代,为了在迭代时提示用户所更新的诊断知识是否存在循环依赖的缺陷,就需要在每次诊断知识迭代时开展缺陷检测,这个检测过程会引入较大的运算量,对于中国空间站这种复杂航天器,该检测过程的运算量将更加庞大,甚至会影响知识更新的实时性。因此,本文在分析故障诊断知识迭代特点的基础上,提出了一种改进Tarjan 算法,以降低循环依赖缺陷检测的运算量。

3.3.1 故障诊断知识的迭代由于故障诊断知识的迭代是以各遥测参数为单位进行的,用户往往针对某个特定的少量遥测参数进行诊断知识的更新,而无需对所有的遥测参数进行故障诊断知识迭代。若可以在对所有遥测参数的诊断知识进行全范围循环依赖缺陷检测前,对一些无需进行全范围搜索即可得出结论的情况进行过滤,就可以极大降低系统的开销。

3.3.2 改进Tarjan 算法

改进Tarjan 算法的核心思想是首先判断某次诊断知识的迭代更新是否改变了有向图Df的SCC 特性,如不改变,则不再进行诊断知识的缺陷检测;同时在每次全范围搜索后,保留各SCC 的记录,并优先检测所迭代遥测参数所属的SCC 是否依然全连通,从而降低进行全范围搜索的可能性。

具体算法如下:

1)初始化时,对有向图Df利用Tarjan 算法搜索得到所有SCC,并记录其中顶点数量≥2 的部分,记录为Qf;

2)当1 个遥测参数的诊断知识更新时,若其旧版诊断知识已检测出存在循环依赖缺陷,则执行步骤3,否则执行步骤5;

3)比对新版诊断知识与旧版诊断知识中相关遥测参数的范围,若范围增大或者保持不变,则提示依然存在循环依赖缺陷,否则执行步骤4;

4)在遥测参数所属SCC 中,再次进行小范围的Tarjan 算法,若依然保持全连通性,则直接提示依然存在循环依赖缺陷,否则执行步骤6;

5)比对新版诊断知识与旧版诊断知识中相关遥测参数的范围,若范围缩小或者保持不变,则提示正常,否则执行步骤6;

6)对有向图Df利用Tarjan 算法重新搜索1 次所有SCC,并将其中顶点数量≥2 的部分更新为Qf,若本遥测参数对应的顶点在更新后的Qf中,则提示存在循环依赖缺陷,否则提示正常。

由上述步骤可知,改进Tarjan 算法并未影响单次Tarjan 执行过程,而是通过步骤3 和步骤5来避免后续较为复杂的Tarjan 执行过程,从而达到降低运算量的目的。

4 算法对比及验证

4.1 算法对比

拓扑排序算法、Kosaraju 算法和Tarjan 算法都 以O(V+E)的时间复杂度判断有向图Df中是否存在环,但Kosaraju 算法和Tarjan 算法还可以得出Df中的所有SCC,这在实际的诊断知识缺陷检测中十分有用,可提示用户进行针对性调整。在不考虑空间复杂度时,由于Tarjan 算法仅需进行1 次深度优先搜索,而Kosaraju 算法则需要进行2 次深度优先搜索,因此Tarjan 算法的执行效率优于Kosaraju 算法。

综合对比后,Tarjan 算法在诊断知识的循环依赖检测中的综合表现更优;而本文提出的改进Tarjan 算法可以有效减少具体执行Tarjan 过程的次数,带来更低的运算开销。

4.2 仿真结果

构造包含500 000 个顶点的有向图,其中分别有6‰、12‰、18‰、24‰、30‰、36‰、42‰、48‰、54‰和60‰的顶点存在循环依赖问题,仿真200 次,其中本文提出的改进Tarjan 算法有1%的可能仅执行步骤3 或步骤5 即可得出结论,则各算法执行时间的对比图如图5 所示。

由图5 可知,拓扑排序算法的耗时最少,但是由于其无法得出Df中的所有SCC,因此无法在实际工作中实际应用;Tarjan 算法耗时优于Kosaraju算法,而本文提出的改进Tarjan 算法较Tarjan 算法更优,且循环依赖越严重,降低运算开销效果越明显。

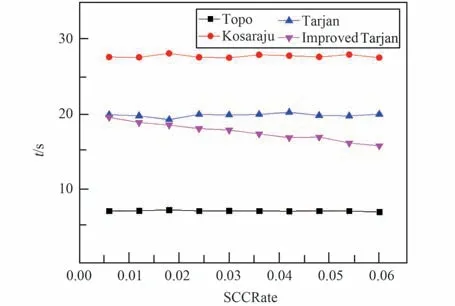
图5 不同算法执行时间对比Fig.5 Comparison of execution time of various algorithms

4.3 改进Tarjan 算法的执行效果验证

将改进Tarjan 算法实际应用于某型号,统计一段时间内仅执行步骤3 或步骤5(无需执行步骤4 和步骤6)即可得出结论的次数,计算得到这些次数相对于总诊断知识迭代次数的比率,如表1 所示。

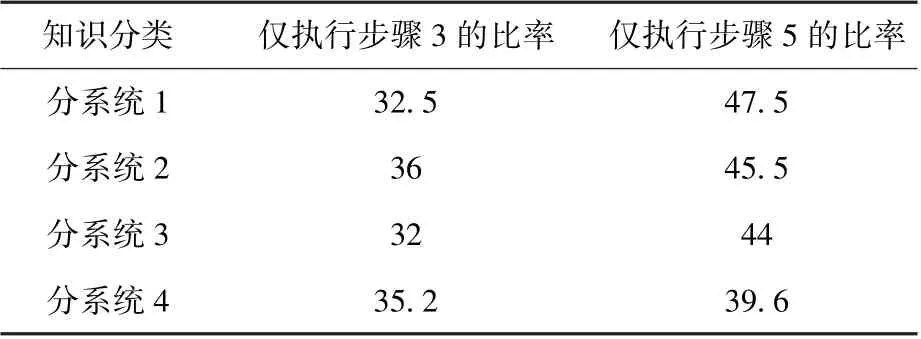
表1改进Tarjan算法仅执行步骤3或5的比例Table 1Therateofstep3onlyandstep5onlyofthe improvedTarjanalgorithm单位:%

如表1 所示,改进Tarjan 算法在实际运行中避免了70%以上的全范围或小范围Tarjan 搜索过程,从而大幅降低了系统的计算开销。

5 结论

航天器下行数据故障诊断系统作为专家系统的一种典型实现,存在知识获取瓶颈。经过分析,一类典型的诊断知识缺陷是不同遥测参数的诊断知识中存在循环依赖。本文通过将诊断知识中的循环依赖检测问题抽象为有向图中的环搜索问题,从而得以应用经典的拓扑排序算法、Kosaraju算法和Tarjan 算法开展诊断知识的缺陷检测,并结合诊断知识经常迭代更新的特点,提出了一种改进Tarjan 算法。

1)将拓扑排序、Kosaraju 算法、Tarjan 算法等经典算法引入问题解决过程,对比发现了Tarjan算法的优势;

2)考虑到诊断知识的迭代以单个遥测参数为单位进行,在Tarjan 算法执行前,对无需执行Tarjan 核心步骤即可得出检测结论的部分进行过滤,设计的改进Tarjan 算法在有效检测诊断知识的循环依赖缺陷的同时,可大幅降低了系统的运算开销。