基于部件级模型修正的某发动机整机动态特性计算

2023-04-26叶莺樱耿斌斌邹宜霖

载人航天 2023年2期

张帆叶莺樱耿斌斌王慧邹宜霖

(1.北京航天动力研究所, 北京 100071; 2.航天科技集团低温推进技术重点实验室, 北京 100071;3.首都航天机械有限公司, 北京 100071)

1 引言

随着中国航天事业持续向深空推进,登月、探火等重大工程有序进行[1],作为空间站新一代载人运载火箭的上面级发动机,高性能氢氧火箭发动机具有不可或缺的战略意义。相较于NASA 等国外机构模拟-试验-修正模拟的多重动强度设计,国内液体动力设计仍停留在以静强度分析考核为主、以故障实例为导向的动强度试验考核为辅的研制流程[2]。这不仅导致发动机推重比较低,而且不能体现结构的薄弱区域。因此,发动机的整机仿真与试验技术已经成为大推力液体火箭发动机研究的主要动力学问题之一[3]。

大型有限元仿真是解决此类问题行之有效的途径[4]。通过预先构建各零部组件模型,再以自由度耦合、弹簧单元等方式对各组件进行耦合连接,形成整机计算模型[5]。优化模型的主要手段就是试验修正,分为基于子结构模态的修正与基于缩比模型的修正[6]。其中基于子结构模态的修正为部件级模态模型修正,对涡轮泵、推力室等零部组件进行模态试验,通过试验结果修正有限元模型,如MC-1 发动机通过喷管延伸段的自由模态试验,以800 Hz 以内的主要频率为目标修正喷管模型[7];基于缩比模型的修正为缩比模型修正,该技术主要应用于火箭、飞机等整体型结构。

现行的模型修正主要分为矩阵法与元素法,矩阵法基于摄动理论建立模型的特征方程,以此修正模型的质量与刚度矩阵[8-9];而参数法更为直接,以材料参数(主要是密度、杨氏模量等)为变量,以模型的静、动特性(主要为位移、应力、模态等)为目标函数,对结构模型进行修正[10-11]。

研制初期受制于加工周期与成本,难以完成整机级振动试验或模态试验,本文提出一种基于部件级的模型修正方案,从部件级的全尺寸三维模型入手,以模态试验或精细计算结果为目标,利用多目标优化修正关键零部件的简化结构,最后拼装成整机计算模型,以提高计算精度。

2 简化模型建立及修正方法

液体火箭发动机结构复杂,涉及加筋旋转壳体、空间桁架、异形壳体等三维结构,且存在管路、转子等局部结构。为避免整机频率淹没在众多局部频率之中,要求既可真实反映结构组成、描述主要特征,又不过多关注细节,保持适中大小的模型。

模型修正引入优化算法,简化模型受简化原则的局限性,动特性误差难以避免。精细化三维模型若应用整机则导致有限元模型过大,计算效率低且不能突出整机频率。因此可采用精细化零部件模型计算结果为优化目标,修正其简化模型,进而搭建整机简化模型。

2.1 简化单元等效方法

为建立大小适中的有限元模型,就要使用低阶、低维单元。某三机并联液体火箭发动机由3 台单机和1 个机架组成,其中每台单机含氢、氧涡轮泵各1 台和2 根零位拉杆。主要使用弹簧单元、梁单元、壳单元、六面体单元、四面体单元与集中质量单元,共6 种单元类型。

整机模型中各组件使用的单元类型见表1。其中氢、氧摇摆软管使用弹簧单元模拟其弯曲刚度,集中质量单元模拟其质量特性,推力室与喷管延伸段使用多层壳单元建模。

表1 整体模型中使用的单元类型Table 1 Element types used in the overall model

2.2 基于多层壳单元的简化准则

对液体火箭发动机,最为重要的简化结构为推力室和喷管延伸段。推力室和喷管延伸段的实际结构并非都是单壁壳体,需用多层壳单元等效。

该发动机推力室身部包括圆柱段、拉瓦尔喷管段以及尾部扩张段,均为3 层结构,内层有沟槽冷却结构,材料为锆铜,外侧为电铸镍身部,如图1(a)所示。

喷管延伸段分为2 段,其中上段管束为变截面设计,管束截面见图1(b),采用管束式排放冷却,主要结构为管束式焊接组件、法兰、进、出口集合器以及一些加强结构(肋板、加强箍等);下段为单壁金属段,上游区域铣有网格,见图1(c),下游设置2 处类工字梁加强箍。

为对各类结构进行统一,使用相同的简化准则,见图1(d)所示,将2 层壁面间的局部结构根据质量和刚度等效原则,通过修改材料参数将中间层等效为连续结构。

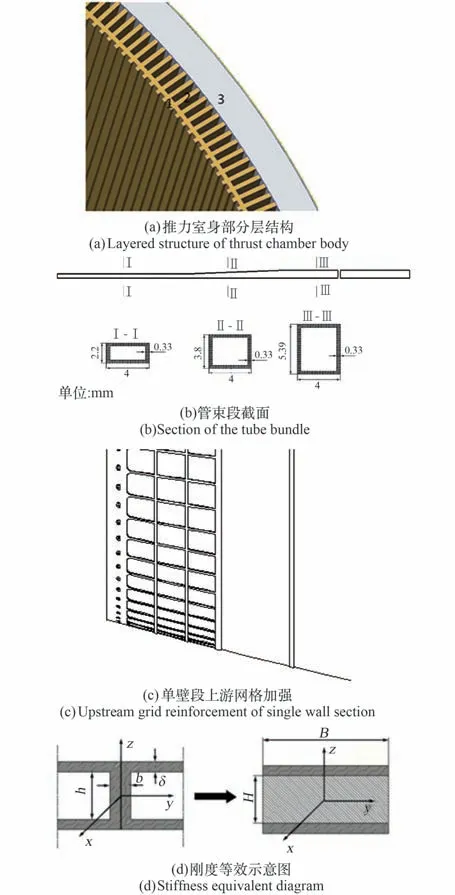
图1 推力室与喷管刚度等效Fig.1 Equivalent thrust chamber and nozzle stiffness

其中密度等效公式如式(1)、(2)所示:

式中,m为总质量,b、h为结构等效前宽与高,H、B为结构等效后宽与高(见图1(d)),ρ、ρd分别为结构等效前、后的结构密度,l为结构长度。

弹性模量等效公式如式(3)所示:

式中,E为结构等效前弹性模量,Ed为结构等效后弹性模量,一般情况下H=h。

2.3 基于MOGA 优化算法的模型修正

多目标优化算法(Multi-objectives Genetic Algorithms,MOGA)是在目标函数受控下找到可接受的优化函数的解,而遗传算法由于其间断性、多峰性以及处理复杂优化问题的有效性,被认为是多目标优化的最优算法[12]。

利用多目标优化遗传算法,以精细化零部件模型计算结果或部件级模态试验结果为修正目标,对零部件简化模型进行修正。其数学模型见式(4):

式中,X为设计变量;F(X)为目标函数;[f1(x),f2(x),…,fn(x)] 为目标函数向量集;gj(x)与hk(x)分别为不等式与等式约束。对于喷管的模型修正问题,使用遗传算法优化的流程图,如图2 所示。

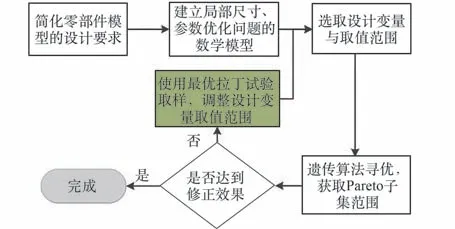
图2 修正模型多目标优化流程图Fig.2 Multi-objective optimization flow chart of the modified model

对于一组最优解集,若这个集合中的解是相互非支配的,则称该集为Pareto 集。若选取设计变量范围内能得到满足状态变量的Pareto 子集,则可以在子集中挑选满意解,若子集为空集,则可以先使用最优拉丁试验进行取样,调整设计变量的取值范围。

利用修正后的零部件模型对整机级/系统级简化模型进行重构。本文计算对象为多机并联液体火箭发动机,对推力室、喷管延伸段等对整机频率影响较大的零部件进行精细化模型修正。

3 大面积比喷管延伸段模型修正

现行可利用的结构简化准则[13]在实际建模过程中存在一些问题。如基于刚度等效的模型简化存在误差,在低频段(100 Hz 以内)吻合较好,高频段难以准确描述。而现有的模型修正方法依赖于大量的模态试验,在发动机研制初期难以实现。

作为目前国内面积比最大的喷管延伸段,该部件特性尚未完全掌握。因此从喷管延伸段入手,建立其未经简化的全尺寸有限元模型,计算其模态频率,以前三阶呼吸频率以及第一阶弯曲频率为优化目标,对简化的喷管延伸段模型进行修正。

3.1 推力室及喷管延伸段简化模型建立

根据式(1)～(3)的简化原则,对推力室、喷管延伸段进行多层壳单元简化。其中推力室从头部沿轴线往下依次为圆柱段、拉瓦尔喷管段与扩张段。圆柱段与扩张段的中间层均为周向分布的288 个肋,拉瓦尔喷管段为周向分布的144 个肋。喷管延伸段的管束段由248 根宽4 mm,壁厚0.33 mm 的变截面矩形螺旋管子组成,根据截面变化可分为3 段。将推力室身部肋结构、管束段中间层进行刚度等效,结果见表2。

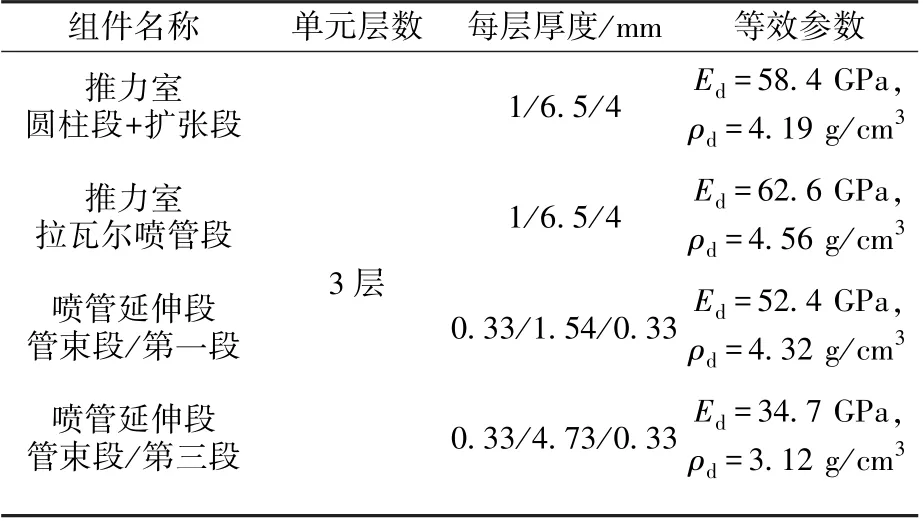
表2 整机模型关键简化参数Table 2 Key simplified parameters of the engine model

3.2 喷管延伸段的计算与试验

分别建立喷管延伸段的全三维有限元模型与简化有限元模型,如图3 所示。在全三维模型中,管束段采用壳单元建模;为模拟焊接状态,在管束外壁面采用共节点建模,内壁面使用2 个节点;喷管法兰、类工字梁加强箍等均采用实体建模。简化喷管模型则完全使用壳单元等效简化,简化模型参数见3.1 节。

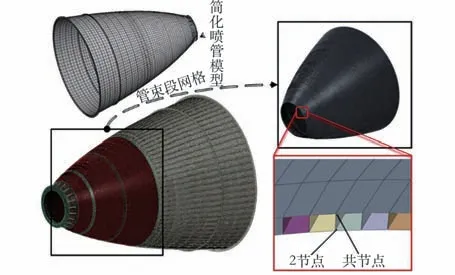
图3 喷管全尺寸有限元网格Fig.3 Full-scale finite element of nozzle

为验证计算结果,对实物喷管进行振动试验,获取其模态频率与振型。

在喷管轴向与周向共分布8 层128 个振动测点,获得喷管前三阶呼吸与一阶弯曲模态信息见图4 所示。在喷管法兰固支条件下简化模型、三维模型计算与振动试验结果对比见表3,振型对比见图5。从对比可以看出,振动试验结果与全三维模型计算结果吻合良好,频率仅存在极小误差,振型吻合。但喷管简化模型除一阶呼吸频率吻合较好外,一阶弯曲、二、三阶呼吸频率均有10%左右的误差,该误差是由于刚度等效过程中刚度偏差不协调引起的。若不对喷管模型进行修正,则在整机计算中会造成整机频率与振型的计算误差。

图4 喷管在振动台试验结果Fig.4 Test results of nozzle on shaker table

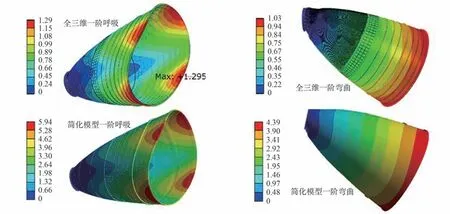
图5 2 种模型喷管模态振型对比Fig.5 Comparison of modal shapes of two model nozzles

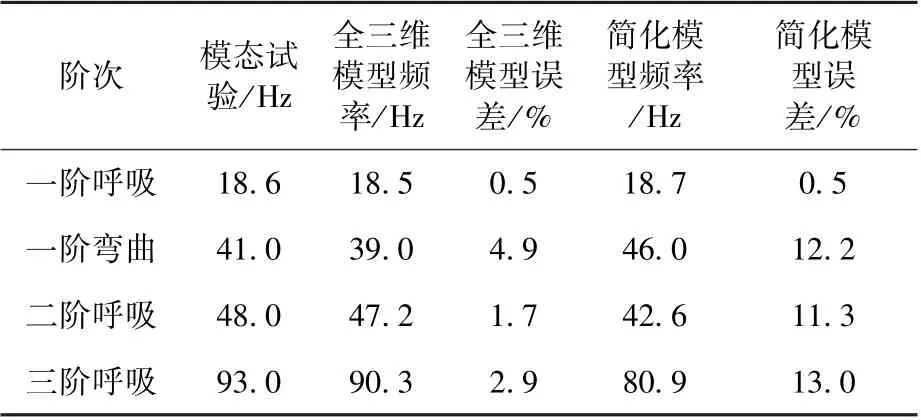
表3 模态频率对比Table 3 Comparison of modal frequencies

3.3 喷管延伸段模型修正

模型修正往往为多轮修正迭代,第一轮以精细化三维模型为目标,第二轮以部件级模态试验结果为目标,第三轮以整机模态试验或热试车结果为目标。从3.2 节的计算结果可以看出一阶弯曲与二、三阶呼吸频率均需修正,若修正整体材料参数会影响一阶频率,故挑选对呼吸频率敏感的局部结构参数工字梁等效厚度与对弯曲频率敏感

的推力室法兰加强壁板厚度作为修正参数。根据2.3 节所述修正方法,结合研制阶段,以精细化三维模型为修正目标,建立喷管延伸段模型修正的数学模型,如式(5)所示:

式中,ω1～ω4为前四阶模态频率,t1、t2为喷管延伸段大端2 处类工字梁加强筋等效厚度,d1、d2为推力室法兰加强壁板厚度。

目标函数为修正模型与全三维模型前四阶频率差值的最小值,状态变量同样为前四阶频率ω1～ω4。从3.1 节的频率对比可以看出修正模型的弯曲模态与呼吸模态均需要调整,因此将设计变量设置为2 处类工字梁加强筋的等效厚度t1、t2与推力室法兰加强壁板厚度d1、d2。

本文模态优化对计算精度要求不高,残差要求较低,可以较快得到不同残差精度下满足要求的几组优化结果,见表4 所示。从表中优化对比结果可以看出,3 组模型修正结果均与原模型较好吻合,综合误差在2.5%以内,挑选误差最小的第1 组作为修正模型值,将修正后的喷管延伸段模型与其他部件进行组合建模,建立优化后的整机模型。

表4 不同残差精度下几组优化结果Table 4 Several groups of optimization results under different residual precisions

4 发动机整机动态特性计算

本文重点关注某三机并联发动机的低频整机特性,在建模中忽略导管、转子、涡轮泵的局部特征,保留推力室、喷管、机架的整体结构。

4.1 整机修正后简化模型建立

从航天飞机主发动机(Space Shuttle Main Engine,SSME)的优化经验看[14],经过组件级模态试验后优化的整机模型动态特性能得到一定改善。本文在喷管延伸段模型修正后,重新搭建整机简化模型,如图6 所示。在该模型中,三机机架与零位拉杆使用梁单元,承力锥与常平座使用实体,推力室、涡轮泵与喷管延伸段均使用壳体建模。该简化后模型结构简单,能反映整机特性,适合求解整机级的动态特性。

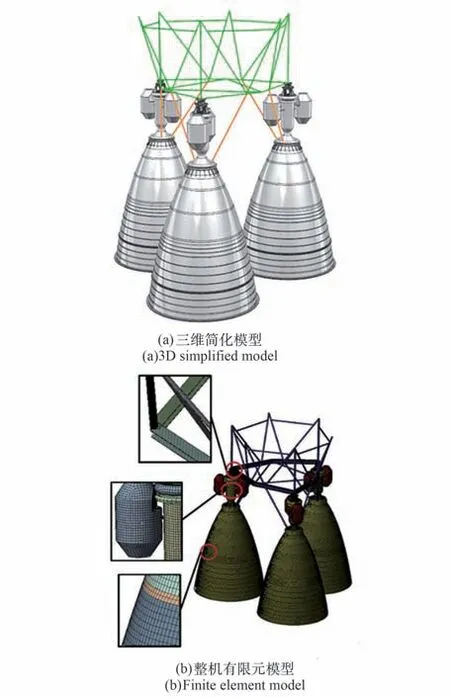
图6 整机装配模型Fig.6 Engine assembly model

将气瓶、燃烧装置等对整机动态特性影响较小部件通过集中质量施加,质量分布见表5。考虑到摇摆软管对发动机模态的影响,借鉴某上面级发动机的摇摆软管建模[13]。摇摆软管为柔性部件,将其简化为弹簧单元,弯曲刚度为38.2 N/mm。

表5 主要部件质量分布Table 5 Mass distribution of main components

需要指出的是,全机除常平座外均为绑定约束,常平座通过自由度耦合,释放沿十字轴轴向的转动自由度,以实现十字轴的自由转动。

4.2 发动机整机模态计算

约束三机机架的6 个上接头位置,计算该边界条件下发动机的模态特性,计算结果见表6 所示,部分典型模态振型见图7 所示。从表6 可以看出,在上述边界下,该三机发动机的整机频率较低,在100 Hz 以内分布大量频率,其中喷管与整机摆动频率均集中在50 Hz 以下,机架频率集中于50～100 Hz,扭转频率分布在5 ～60 Hz,呼吸频率在频率区间均布。从图7 可以看出整机模态振型可以分为单机摆动、单机扭转、整机摆动、整机扭转、机架扭摆以及喷管呼吸等几大类。

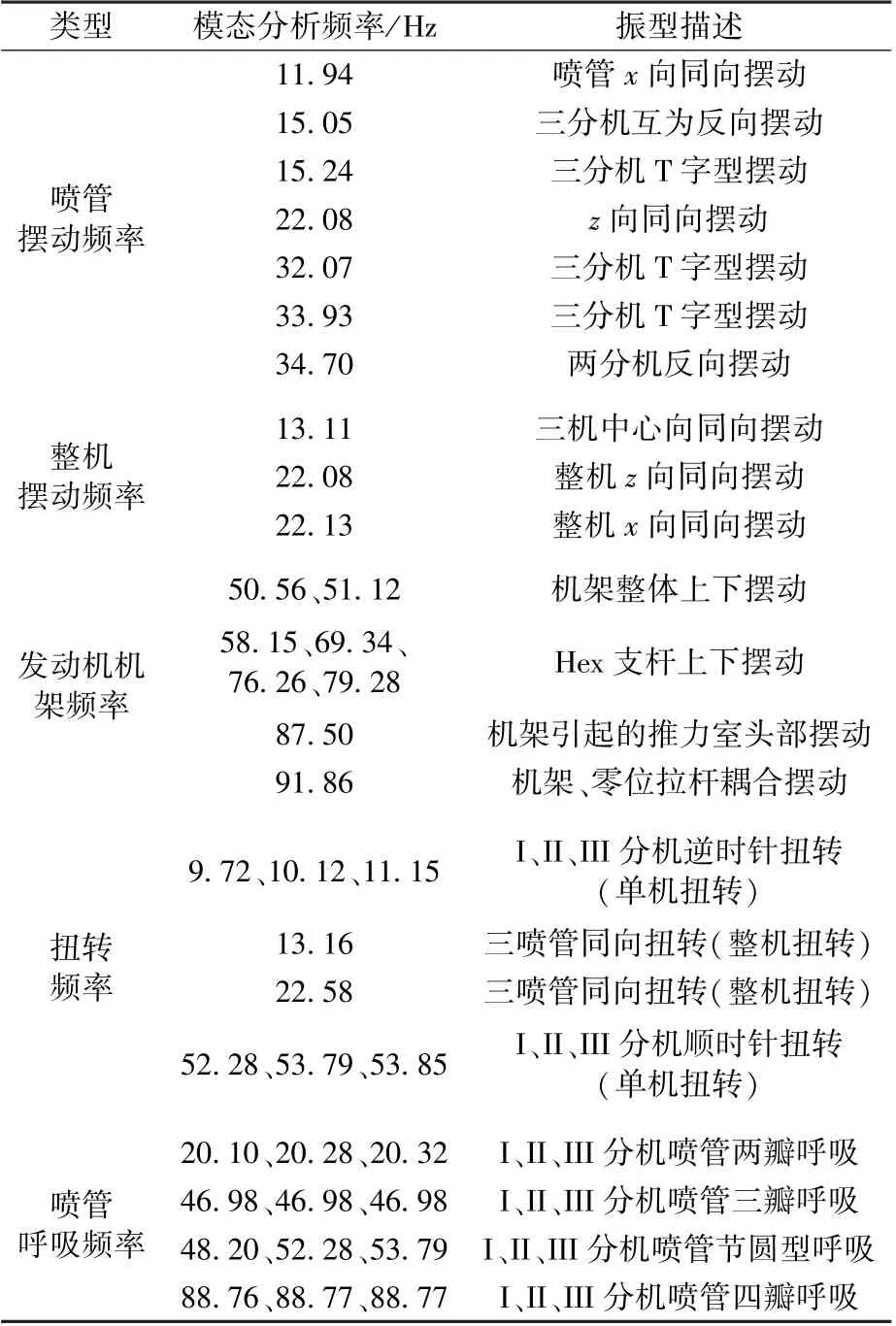
表6 整机模态分析结果Table 6 The modal analysis results of the whole machine

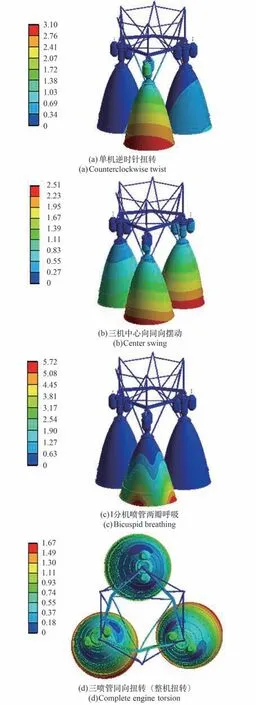
图7 三机部分典型模态振型Fig.7 Typical modal shapes of parts of three engines

经过计算发现,零位拉杆刚度、推力室喉部刚度分别对发动机一阶、二阶摆动频率影响较大。如零位拉杆外径增加1 mm,整机前两阶摆动频率分布提高2 Hz、5 Hz;而考虑推力室喉部加强环前后的三机中心向同向摆动频率从10.28 Hz 提高到13.11 Hz。整机安装状态下,大喷管呼吸频率与喷管法兰固支下的频率基本相同,通过与某上面机发动机对比,发现喷管面积比的增大会造成喷管的呼吸频率、整机摆动频率都往更低频集中,增加加强肋、类工字梁加强箍等喷管壁面加强结构可以解决该问题。

4.2 关键点位正弦扫描(谐响应)计算

根据模态计算结果,取8 ～100 Hz 范围内共64 阶模态,结构阻尼比取0.02。在8 ～100 Hz 范围内在整机轴向施加鉴定级正弦扫描试验条件,幅值为2.0g。并且参照某上面级发动机测点位置,绘制机架各类拉杆端点、推力室头部以及喷管延伸段等部件的频响特性曲线,见图8 所示。

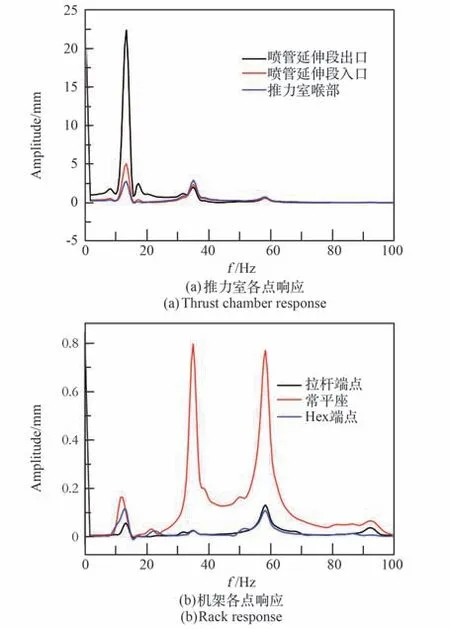
图8 部分测点位置频响特性曲线Fig.8 Frequency response characteristic curve of some measuring points

从图8 可以看出,推力室+喷管的响应主要集中在13.34 Hz 附近,根据柱坐标下的分响应可判断此频率为整机的摆动频率,此时喷管延伸段出口最大位移幅值为22.34 mm,其中径向分量为17.4 mm,由于发动机内部的结构非线性,实际响应应低于此值。此外,在35.0 Hz 与58.4 Hz 均有较小量级的响应峰,喷管延伸段入口、推力室喉部的峰值频率与延伸段出口基本相同,幅值较小。机架选取各类拉杆端点,因此整体响应幅值较小,其中机架与常平座对接接头处有较大响应,主要响应频率有11.67 Hz、35.0 Hz、58.4 Hz 等。幅值最大约为0.8 mm,而机架的响应较推力室明显在更高频区域集中。