多平台协同侦察定位技术研究

程 翔

(海军装备部驻扬州地区军代室,江苏 扬州 225101)

0 引 言

无源侦察定位系统是在自身不发射电磁波的情况下,利用辐射源目标发出的辐射信号进行测量,来获取辐射源的位置,具有电磁静默、战场生存能力强、复杂电磁环境适应能力强等特点。在现代战场环境中,无源侦察定位技术的使用不仅增强了我方的作战能力,同时也提高了我方平台的生存能力。现代战争的战法正在由单一平台和单一传感器向多平台及多传感器的方向发展,无源侦察定位技术在电子战中有着广泛的应用并发挥了重要作用,备受各国的重视并在现代战争中占据着重要的地位。各国都在不断提高侦察定位系统在复杂环境下的适应能力,目前使用较多的多平台定位方法为交叉定位法和时差定位法。

测向交叉法又称三角定位法,通过高精度的测向设备在2个或2个以上的观测站对辐射源进行测向,然后根据各观测站测得的数据以及观测站之间的距离,经过几何的三角运算便可确定出辐射源的位置。测向交叉定位系统至少由2个观测站组成,每个站都配有精密的测向系统,每个站测到的辐射源方位角构成了平面上连接辐射源与观测站的直线,2条直线的交点就是辐射源所在位置,定位精度主要取决于测角误差、站址误差、平台位置关系等。

时间差测量定位系统则是利用多个位置的接收机接收某个未知位置的辐射源信号来确定该辐射源的位置。多平台时间差测量定位技术的基本问题是:给定一组平台及其时间差测量值,如何快速、有效和准确地确定目标的位置[1]。

1 协同定位原理及误差分析

1.1 测向交叉定位原理及误差分析

1.1.1 测向交叉定位原理

测向交叉技术又称三角定位法,在各种平台上均有实现应用,是一种经典而成熟的无源定位技术。相对而言,在当前愈加密集复杂的电磁环境下测向交叉法也是一种比较稳定可靠的定位技术,因为在复杂电磁信号环境中目标辐射源的方向角是一个缓慢变化的参数。在测向交叉中,对目标到达角的测量是实现目标定位的先决条件,辐射源位置以及测向观测站的位置如图1所示。

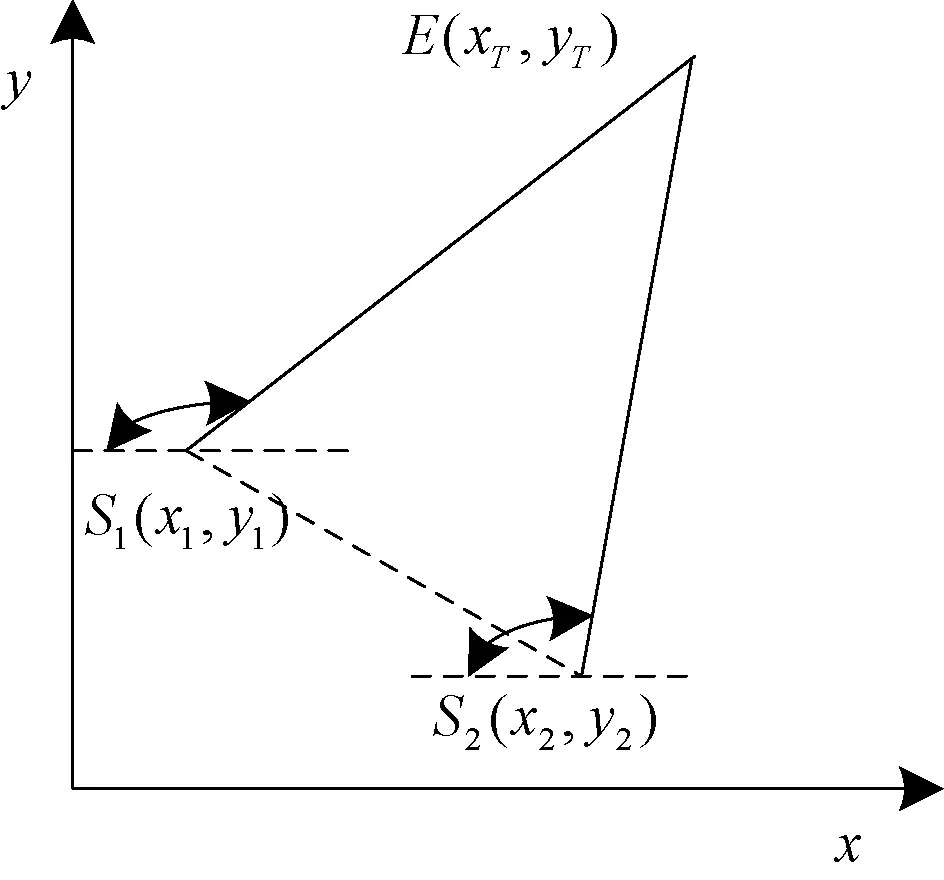
图1 辐射源与测向观测站的位置分布

若以X轴的负向为测向基准,由图1可得到几何关系为:

(1)

式中:θ1是目标E相对于S1的方位;θ2是目标E相对于S2的方位。

求解方程组可以得到:

(2)

1.1.2 协同定位误差描述方法

协同定位误差的大小分布与具体的定位场景、可观测性、定位方法、参数测量误差等密切相关,是协同侦察定位系统的重要指标之一。由于目标辐射源的位置不同,即使相同的测角误差在不同位置所交的区域也不相同。如果测向观测站的站址固定,定位误差还是目标位置的函数,为了更好地描述这种关系,工程上定义为定位误差的几何稀释度,或者称为定位误差的集合分布[2],如公式(3)和(4)所示,分别表示二维和三维情况:

(3)

(4)

几何精度因子(GDOP)描述的是定位误差的分布,它既可以用均方根误差来表示,也可以用圆概率误差来表示。为了更直观地表示目标定位误差的分布,通常将一个区域的定位误差分布GDOP描绘成等高线图的形式,并在其上面标示等高线数值。

由于引起定位误差的因素是多方面的,根据中心极限定理,定位误差一般服从正态分布,它们的统计性质往往可以利用分布函数的一、二阶矩阵来表示。所以可以利用联合高斯分布来近似描述定位误差的分布,对于二维定位的情况,假定定位误差服从二维正态分布,其概率密度函数为:

(5)

每次使用复杂的概率密度函数来描述定位误差过于繁琐,为了进一步简化定位误差的描述,可以用一个与概率p相联系的置信椭圆(称为概率误差椭圆)来描述定位误差。该椭圆的大小和形状说明了定位误差的情况,椭圆越大定位误差越差。在实际应用过程中,描述一个椭圆需要长轴、短轴和方向等参数,使用不便,所以在无源定位的误差分析中,还是用定位误差圆来描述定位误差,如图2所示,概率误差椭圆的来源如图3所示。

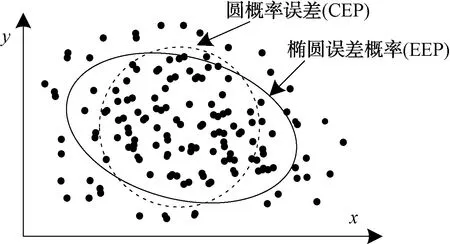
图2 椭圆概率误差与圆概率误差分布图

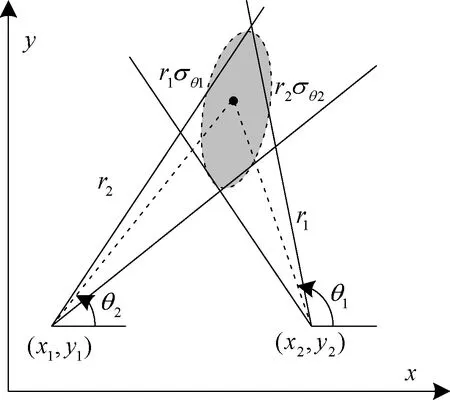
图3 概率误差椭圆

圆概率误差是指以定位估计点的均值为圆心,且定位估计点落入其中的概率为0.5的圆的半径[3],定义为:

(6)

在误差不大于10%的情况下,CEP可近似表示为:

(7)

利用定位误差圆的半径可说明定位误差的大小,但不能说明定位误差的分布情况,而GDOP则可以说明定位误差的分布情况。

1.1.3 测向交叉定位误差分析

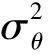
(8)

利用各个单项误差的标准差合成计算总的标准差具有简单的优点,同时还不用考虑各个误差的概率分布,由误差合成理论可得到:

(9)

取50%圆概率误差,则CEP可表示为:

(10)

若以两基站连线所在直线为水平参考轴,则上述公式可以简化为:

(11)

交叉定位精度与多种因素有关,除了与测向精度有直接关系外,还与目标和2个观测站构成的三角形形状有很大关系。

1.2 时差定位原理及误差分析

1.2.1 时差定位原理

时差定位是根据同一辐射源信号脉冲到达各个观测站的时间差来对该辐射源进行定位的,由于观测站无法直接接收到辐射源信号脉冲的发射时间,因此只能通过测得辐射源信号相同脉冲到达不同观测站的时间差来进行定位。通常需要3个或3个以上的观测站得出2个或多个时差,来构成多个双曲面。当只有3个观测站时,需要加入地球球面方程这个约束条件来构成定位方程组进行求解定位。而对于四站时差定位系统,3个时差方程构成了3个双曲面,这3个双曲面相交于一点,该点即为所求辐射源位置[5]。三站时差定位的原理框图如图4和图5所示。辐射源信号到达主站C、辅站B与到达辅站A的时间差为:

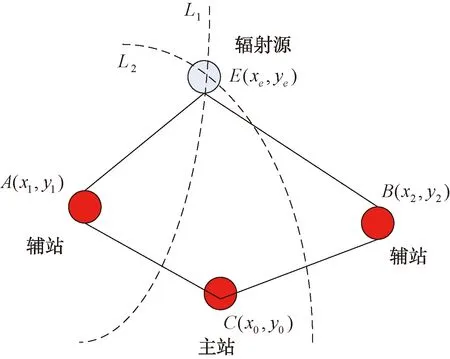
图4 时差定位观测站布置框图

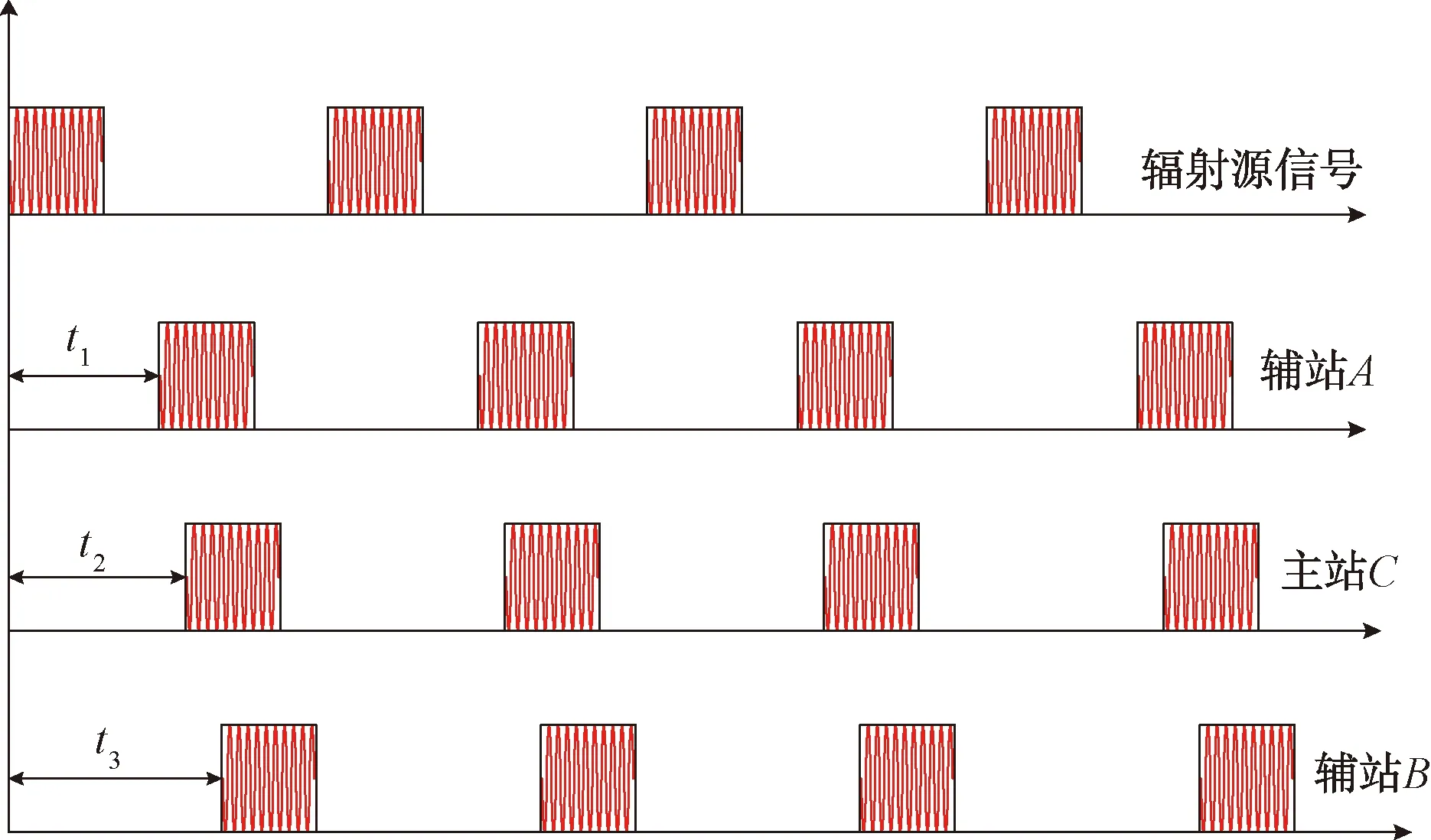
图5 辐射源信号到达各个观测站的时序框图

(12)

平面上的2个观测站收到同一雷达发射脉冲的时差可以确定1条双曲线,平面上的3个观测站时差定位可以产生2条双曲线,双曲线的交点即为目标的位置。时差定位的定位精度远高于测向交叉定位,但是时差定位的定位精度受时差测量精度和观测站间的集合位置关系限制。

假设空间3部接收机的位置为(xi,yi)T,i=0,1,2,其中i=0表示主接收机,i=1,2表示辅接收机,辐射源的位置为(x,y)T,则定位方程表示为:

(13)

式中:i=0,1,2;ri表示辐射源与第i个接收机的距离;ri0表示辐射源到第i个接收机与其到主接收机之间的距离差;Δti表示目标辐射源到达第i个接收机与到达主接收机的时间差。

1.2.2 时差定位精度分析

时差定位是根据同一辐射源信号脉冲到达各个观测站的时间差来对该辐射源进行定位的,由于观测站无法直接接收到辐射源信号脉冲的发射时间,因此,只能通过测得辐射源信号相同脉冲到达不同观测站的时间差来进行定位。时差定位的定位精度主要与接收机测量的到达时精度相关,在外部同步时钟稳定的情况下,接收机到达时的测量精度主要与接收机内部时钟稳定度、噪声引起的测量误差、接收检测处理带来的测量误差等相关:

(14)

式中:σ为不考虑同步精度的到达时间(TOA)测量误差;σ1表示接收机内部时钟稳定度带来的TOA测量误差;σ2表示由噪声引起的TOA测量误差;σ3表示由接收机检测处理带来的TOA测量误差。

时钟稳定度带来的测量误差:如果时钟采用铷钟,时钟的稳定度可以达到10-11,每秒钟的稳定度可以达到10 ps,如果外部同步时钟进行秒复位,则由内部时钟带来的TOA测量误差为10 ps,基本可以忽略不计。如果时钟采用晶振,时钟的稳定度可以达到10-7,每秒钟的稳定度可以达到100 ns。如果外部同步时钟进行秒复位,则由内部时钟带来的TOA测量误差为1 μs。所以在进行高精度到达时测量时,需要选用时钟稳定度更高的铷钟。

噪声引起的TOA测量误差:大多数接收机采用过门限时刻作为TOA的测量值。接收机热噪声以及外部环境引入的传输噪声将导致理想脉冲波形受随机噪声的影响,引起过门限时刻的测量误差。在高信噪比条件下,该误差项可表示为:

(15)

式中:tr为脉冲上升沿时间(脉冲前沿包络从脉冲幅度的10%增加到90%过程的持续时间),tr的典型值为10～100 ns;σSNR为信噪比。

可以看出,脉冲上升越快,信噪比越高,则测量误差σ1越小;反之σ1越大。通过仿真分析可知,噪声引起的TOA的测量误差通常小于5 ns。

检测处理带来的计算误差:接收机的检测处理带来的计算误差主要与采样率及快速傅里叶(FFT)算法积累的点数等相关,目前高精度到达时的检测算法带来的计算误差通常小于5 ns。

在分析计算时,TOA的测量误差体现的就是目标与观测站的位置误差,为了分析方便,把式(13)写成如下形式:

(16)

对上式中的ri0=ri-r0=c(ti-t0)等号两边取x,y,xi,yi的微分,得到差定位的误差公式:

dri0=dri-dr0=

(17)

2 协同定位误差仿真分析

2.1 交叉协同定位误差仿真分析

假设两站侦察设备对目标观测的测向精度均为1°,则当两站相距为25 km 时,圆概率相对误差的分布情况分别如图6所示。图中黑线为与两基站法线夹角±30°的位置。

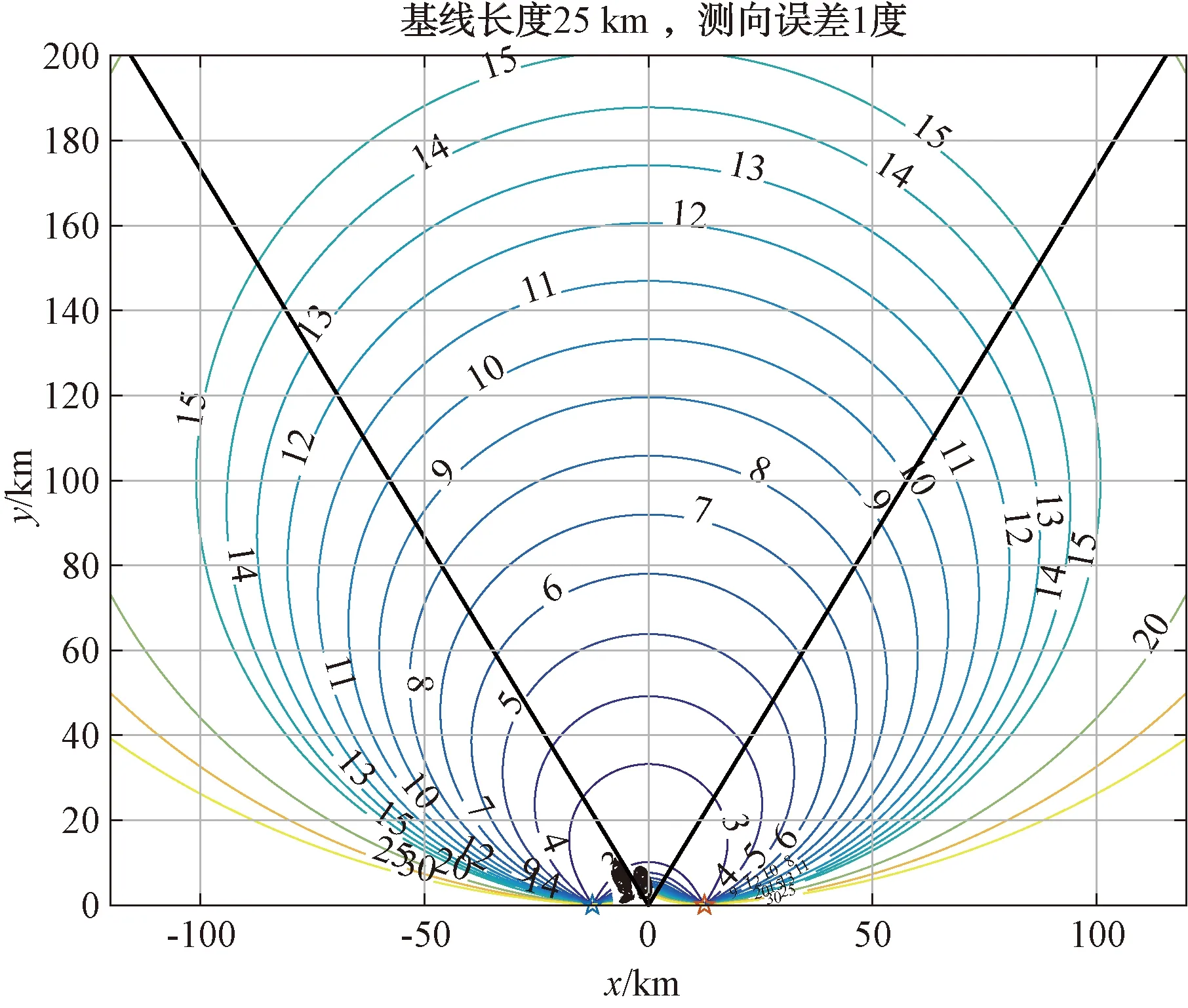
图6 两站相距25 km对目标定位情况

首先考察目标位置与定位基线间的几何关系对定位精度的影响。设定仿真条件:定位系统的测向误差为0.5°,两观测站位置分别设于S1(-30 km,0),S2(30 km,0)。目标E的位置沿着与x轴方向均匀变化,且与x轴距离分别为50 km、80 km和100 km。双站交叉定位误差与x轴方向上的变化曲线如图7所示。

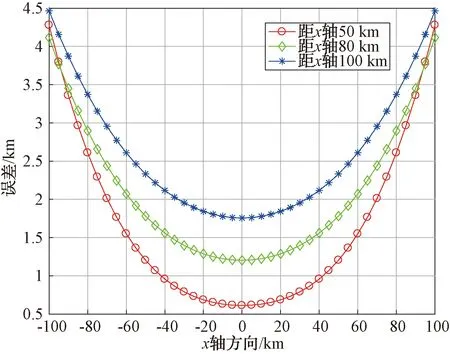
图7 定位误差在x轴方向上的变化曲线

接着仿真分析双站交叉定位精度与侦察距离L、波束夹角的关系。目标位置固定:(0,100 km),两站侦察距离相同,测向误差仍为0.5°,定位误差曲线见图8。

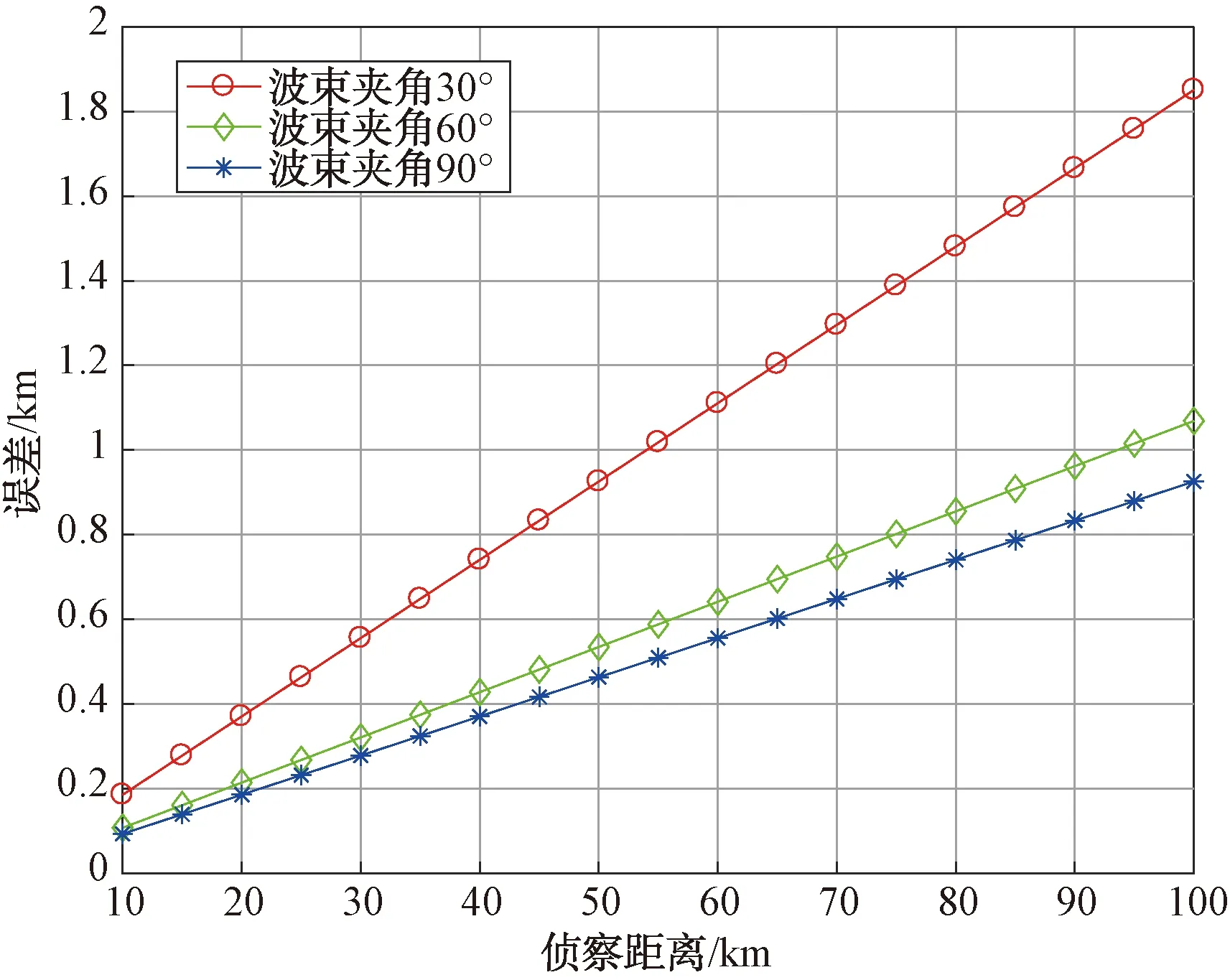
图8 定位误差曲线图

最后分析定位基线长度和测角精度对定位精度的影响,设定目标位置不变,坐标为(0,100 km),分别改变定位基线长度和测向精度,计算相应的误差结果如表1所示。

表1 不同基线长度和测向精度下测向交叉定位的定位误差

分析图6、图7、图8的仿真结果可得到如下结论:

(1)当目标位于定位基线的中垂线方向上时,定位精度最高。

(2)测向精度越高,定位基线长度越大(目标与双站构成的波束夹角不变时),越有利于提高定位精度。

(3)双站测向交叉定位误差大小与波束夹角和侦察距离有关,波束夹角越大(90°范围内),侦察距离越小,越有利于减小定位误差,即抵近侦察时定位精度高。

2.2 交叉协同定位误差仿真分析

本节通过仿真试验验证时差定位算法的性能,分别仿真验证算法的性能和不同位置的GDOP。

首先验证算法的定位效果,三接收站布阵方式为等边三角形,主站位于原点处,边长为40 km,系统测时误差为100 ns,站址误差为10 m,分别验证目标位于点x1(0,100 km)和x2(40 km,100 km)2个点的时差定位效果如图9、图10所示。

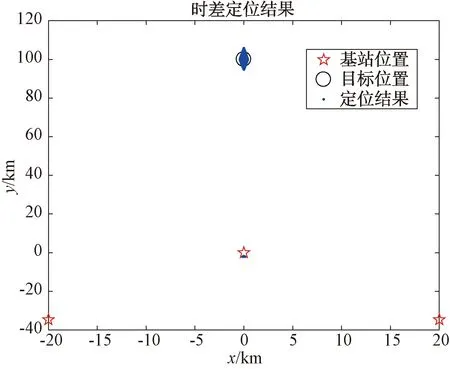
图9 点x1(0,100 km)定位效果

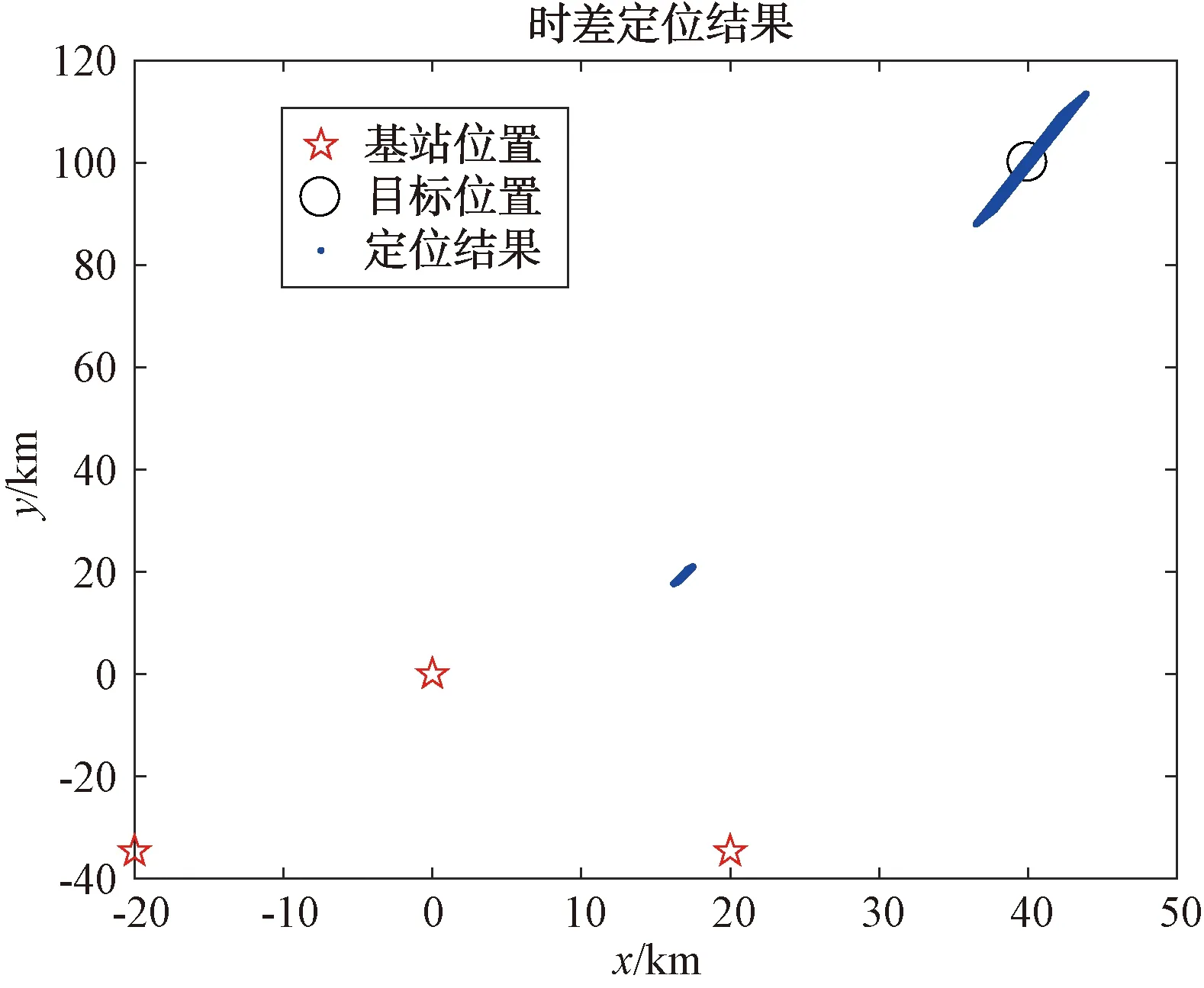
图10 点x2(40 km,100 km)定位效果

从上述仿真结果可以看出,当存在测时误差和站址误差时,目标定位结果落在距离真实位置一定范围内,形成一个菱形区域。对比图9和图10,不难发现,当目标处于三角形中垂线上时,具有较高的定位精度,而当目标位于两接收站延长线上时,此时定位精度较差。

接下来验证时差定位的GDOP,由于布阵方式不同,形成的GDOP分布图也相差较大。图11为直线布阵时的GDOP,图12为三角形布阵的GDOP,图13为y轴上2种布阵的GDOP对比。

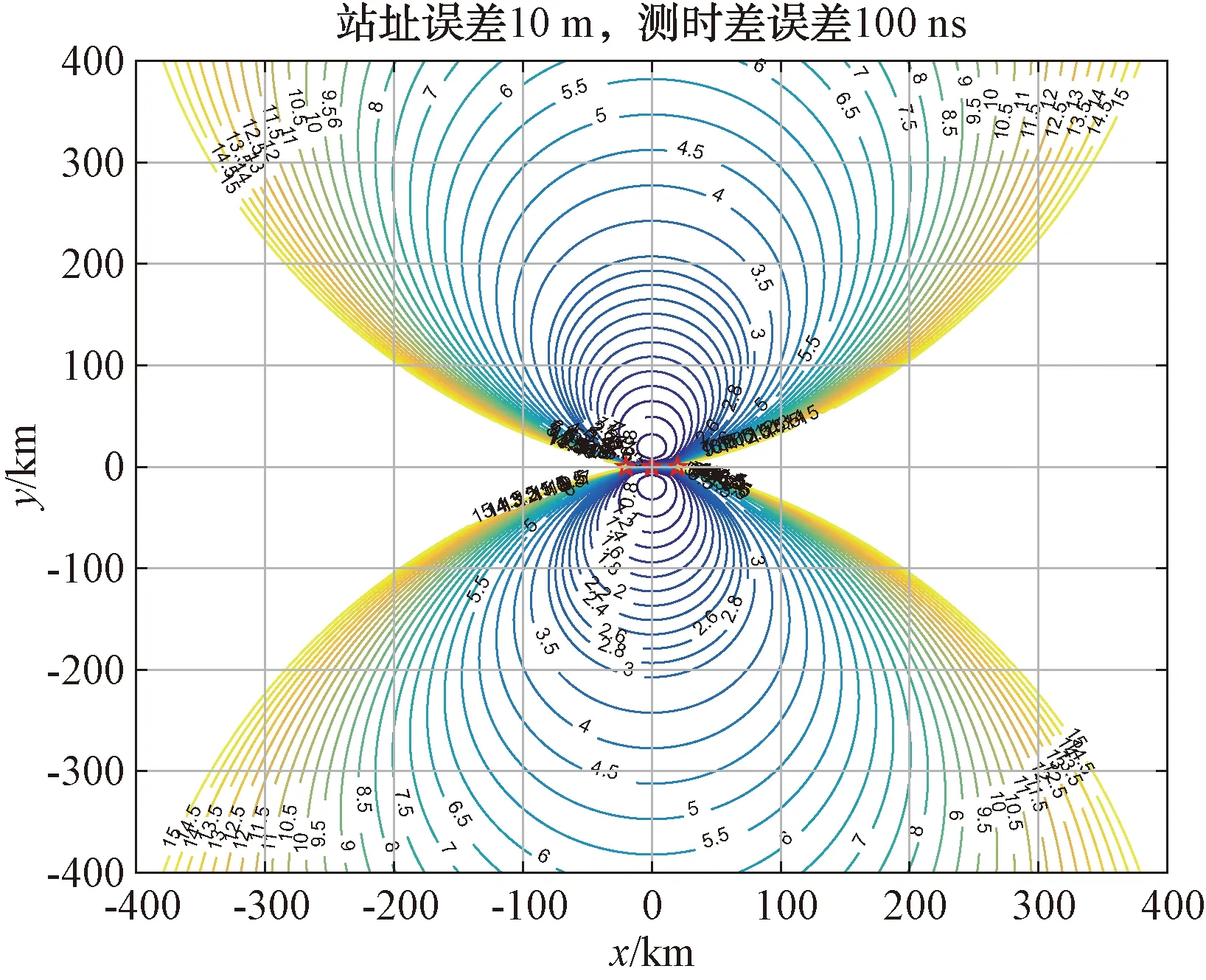
图11 直线型布阵

图12 等边三角形布阵

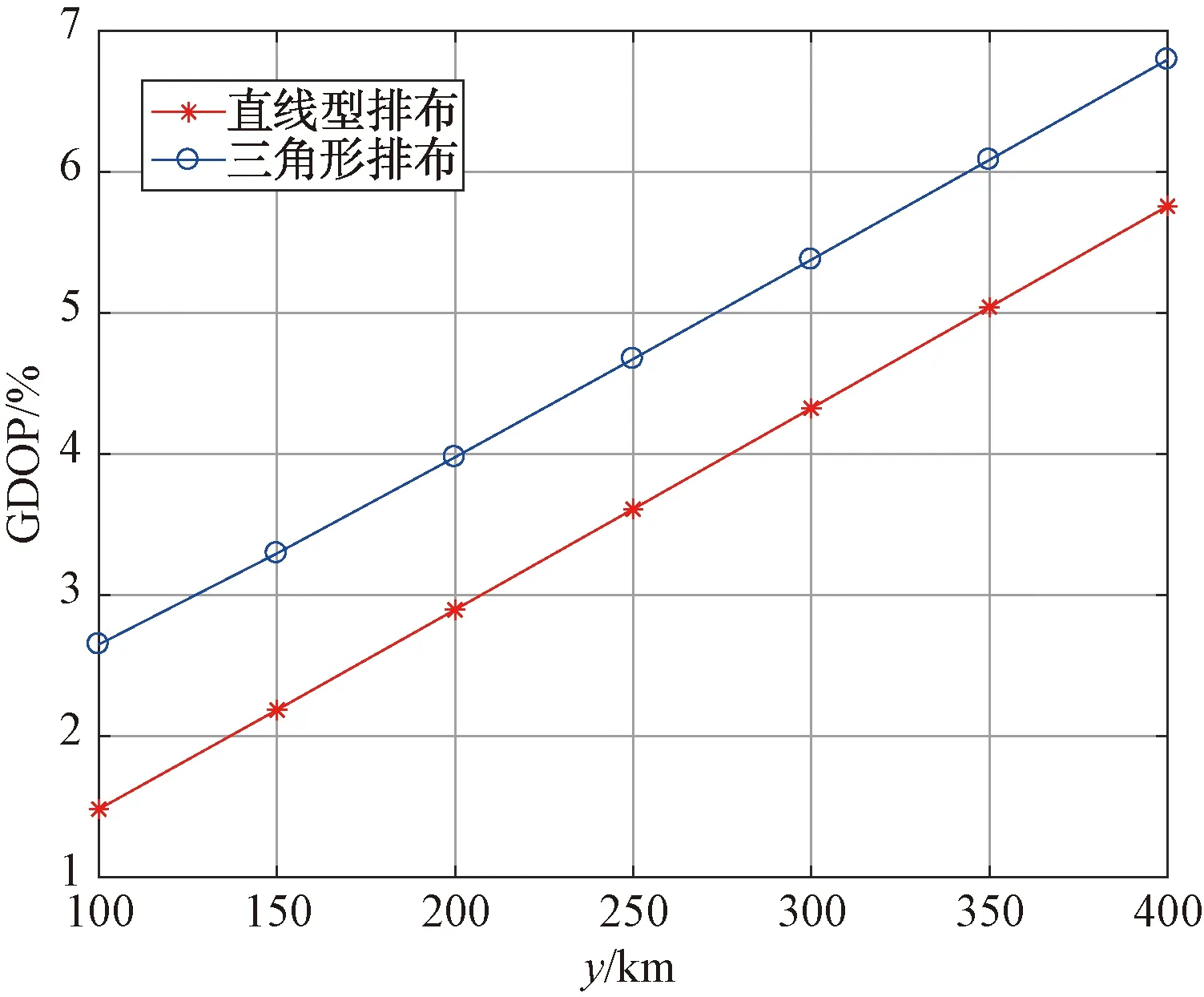
图13 2种布阵GDOP对比

由图11、图12仿真结果可知,当进行三基站时差定位时,定位误差分布和三接收站中两两接收站连线所形成的夹角密切相关,在该夹角区域内,定位精度较高,而在每2个接收站连线延长线所在的区域,无法进行时差定位。从主接收站的角度来看,当其与2个辅接收站连线所形成的夹角越大,则主接收站前方连续定位区域越大,且定位精度较高。因此,在进行编队作战时,编队的布局应该根据战术需求制定。例如,当侦察目标侧重于某地域一侧时,那么编队布局可以选择近似直线布置方式,以便在侦察区域获得定位精度较高且作用地域较广的区域。

最后验证时间同步精度对时差定位精度的影响,时间同步精度分别取50 ns、100 ns、150 ns和200 ns,站址误差为10 m,布阵采用三角形布阵方式,对比距离主站不同位置处的GDOP,仿真分析如图14所示。

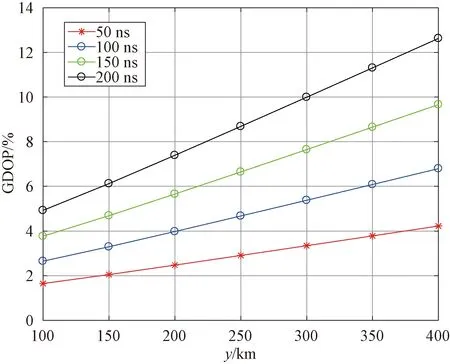
图14 不同时间同步精度下的GDOP

从图14不难发现,随着侦察距离越来越远,时差定位精度也缓慢下降,距离主站400 km、时间同步精度为50 ns时,时差定位精度小于6%R;当时间同步精度为100 ns时,时差定位精度小于9%R;当时间同步精度为200 ns时,时差定位精度小于15%R,满足实际工程应用中的定位精度要求。

从以上分析可以看出,在到达时精度有保障的条件下,时差定位精度要比交叉定位精度高。在工程实现上,交叉定位相对简单,两站就可以实现交叉定位,实现交叉定位可在辐射源描述字(EDW)级别上实现。而时差定位虽然定位精度较高,但是需要三站同时收到相同的脉冲进行时差比对,在实际使用中存在共视问题,使用局限性较大。所以,在工程中可以结合交叉和时差定位的优缺点,采用交叉和时差联合定位方法。

3 结束语

多平台交叉定位和时差定位是无源定位的重要技术手段,在工程中有着广泛的应用。本文研究了多平台交叉定位和时差定位的基本原理,通过仿真验证了交叉定位和时差定位在不同布阵方式、不同测向精度以及不同同步时间精度下的性能。对比分析了交叉定位和时差定位在工程时间中的优缺点,为工程实践提供了一定的参考。后续需要继续研究交叉、时差联合定位方法,时差、频差联合定位方法,解决单一定位方法所带来的局限性。