高速直齿轮齿面有限元网格精准离散方法

2023-04-11黄一伦胡玉梅

重庆理工大学学报(自然科学) 2023年3期

黄一伦,陈旭,胡玉梅

(1.重庆理工大学车辆工程学院, 重庆 400054;2.重庆大学机械传动国家重点实验室, 重庆 400044)

有限元作为一种常用的齿轮啮合仿真分析方法,被广泛应用于齿轮动力学性能的研究,其中齿轮齿面在进行有限元网格离散时,网格的大小对于齿轮啮合有限元仿真结果的正确性影响很大。在过去几十年间,国内外许多学者针对齿轮有限元网格离散的问题展开了研究。刘更等[1-2]通过程序编写出不同的齿廓网格节点生成函数,根据计算得到的节点坐标自动生成轮齿有限元网格。穆慧勇等[3]将斜齿轮齿根中点拉应力值取得平衡时的初始网格密度作为齿面齿向网格密度。张涛等[4]通过ANSYS的参数化程序语言,利用8节点六面体单元对齿轮进行有限元离散。曹雪梅等[5]利用刨齿展成法精确计算出齿面节点坐标,在旋转投影平面上划分网格,最终映射到齿面上。李红勋等[6]综合计算时长、精度和收敛性等因素,将齿面网格细化,而轮毂基体网格设置较稀疏。Coy等[7]提出了一种考虑赫兹变形影响的齿面网格尺寸选择方法。Vijayakar等[8]通过结合曲面积分法和传统有限元分析方法研究了齿轮齿面的有限元网格离散问题。Gonzalez-Perez等[9-11]研究了考虑齿轮扭转变形和轴偏转影响时的有限元网格划分方法。Gonzalez-Perez等[12]提出了一种基于多点约束的齿轮传动有限元模型网格细化策略。

综上所述,国内外学者对齿轮有限元网格离散研究已经取得了丰硕成果,然而这些研究并未考虑齿面有限元网格尺寸在高转速下的适应性问题。随着现代航空航天技术的不断发展,高线速直齿圆柱齿轮作为航空发动机动力传输的关键零部件具有质量轻、转速高和载荷大等特性,其服役过程呈现强烈的非线性和瞬态性,所以对该类齿轮齿面有限元网格离散化的精度提出了更高要求。为此,本课题组用两圆柱滚子曲面接触有限元模型来模拟齿面接触,通过有限元仿真分析不同转速下两圆柱滚子接触产生的滑移能损失,提出一种齿面网格大小能够适应齿面滚滑速度以及曲率半径变化的齿面有限元网格精准离散方法。

1 齿面啮合简化模型

在齿轮啮合过程中,轮齿之间的接触属于2个曲面之间接触,而曲面有限元离散的基本思想是用有限个单元去近似模拟连续光滑的曲面体,要达到同等的离散化精度,曲率半径越小的曲面,所需要的单元网格尺寸也越小。此外,高线速直齿轮转速较高,齿面有限元网格存在较大的离心力,导致齿面有限元模型在参与啮合时会产生单元网格之间的冲击振动,这与实际的齿面接触存在一定误差。所以要想建立精确的齿面接触有限元模型,关键问题是找到在不同转速下齿面有限元网格尺寸与齿面曲率半径之间的最佳倍数关系。

滑移能损失是2个相对滑动的面碰撞所导致的能量交换,不可避免。曲面接触的滑移能损失与摩擦系数及正压力有关,理论滑移能损失E可以表示为:

E=f×F×Vt×t

(1)

式中:f为接触摩擦系数;F为垂直载荷,N;Vt为两接触面的相对滑动速度,m/s;t为时间,s。齿轮啮合过程中的能量损失主要来源于轮齿之间的滑移能损失,所以轮齿之间的滑移能损失在一定程度上能够反映出轮齿之间的接触状态。由于齿面上不同啮合位置处的齿面压力以及相对滑移速度均不相同,所以理论求解齿面滑移能损失存在一定难度。直齿轮的渐开线齿廓本质上是由一系列曲率半径不同的圆弧所组成的光滑曲线,并且齿面接触区宽度远远小于接触区域的曲率半径,因而可以对啮合齿面作适当简化。根据Weck等[13]试验结果表明,在相同工作条件下,啮合轮齿之间的接触状态可以简化为2个圆柱滚子沿其母线方向上的接触,如图1所示。图1中圆柱体滚子的半径R1、R2分别代表齿轮啮合位置处的齿面曲率半径;n1和n2为圆柱滚子的转速,上下圆柱滚子接触点处的线速度分别代表主从轮齿齿面在啮合位置处的切向速度;圆柱滚子垂直向下的压力F代表齿面啮合位置处的法向载荷;b代表齿宽。

图1 圆柱滚子曲面接触模型简图

2 直齿轮啮合几何分析

圆柱滚子曲面接触模型能精准模拟高线速直齿圆柱齿轮齿面啮合的前提是对其施加准确的边界条件以及设置合理的几何参数,其中包括圆柱滚子的曲率半径、转速以及垂直载荷,而这些边界条件和几何参数的值与高线速直齿圆柱齿轮的齿面曲率半径、齿面切向速度、相对滑移速度以及齿面法向载荷的大小密切相关。本课题组根据直齿圆柱齿轮渐开线齿廓的啮合过程,通过理论推导得出这些参数的计算方法。

图2为直齿轮齿廓啮合过程示意图。P为节点,K1点和K2点是啮合线上任意位置啮合点。N1N2为理论啮合线,B1B2为实际啮合线,主动轮从B1点进入啮合并推动从动轮的齿顶旋转,从动轮在B2点与主动轮齿顶脱离啮合。

图2 齿轮齿廓啮合过程简图

根据齿廓啮合过程中的几何关系可知,齿面上任意啮合点的曲率半径等于齿面渐开线的发生线长度,即图2中啮合点距离N1点或N2点的长度,所以任意啮合点在主、从动轮上的曲率半径可以表示为:

(2)

(3)

式中:ρ1为任意啮合点在主动轮上的曲率半径;ρ2为任意啮合点在从动轮上的曲率半径;α为分度圆压力角;r1为主动轮分度圆半径;r2为从动轮分度圆半径;rk为任意啮合点在主动轮上的半径;rb1为主动轮基圆半径。

图2中的V1k、V1t、V1n分别是啮合点K2在主动轮上的绝对速度、切向速度以及法向速度,根据任意啮合点K2在主动轮上的速度矢量三角形与直角三角形⊿K2O1N1的相似关系,主动轮上任意啮合点沿齿面的切向速度V1t可以表示为:

(4)

式中:n1为主动轮转速,r/min;ρ1为任意啮合点K2在主动轮上的曲率半径,mm;V1t为主动轮上任意啮合点K2沿齿面的切向速度,m/s。

图2中的V2k、V2t、V2n分别是啮合点K2在从动轮上的绝对速度、切向速度以及法向速度,根据任意啮合点K2在从动轮上的速度矢量三角形与直角三角形⊿K2O2N2的相似关系,从动轮上任意啮合点沿齿面的切向速度V2t可以表示为:

(5)

式中:n2为从动轮转速,r/min;ρ2为任意啮合点K2在从动轮上的曲率半径,mm;V2t为从动轮上任意啮合点K2沿齿面的切向速度,m/s。

主、从动轮任意啮合点处的相对滑移速度Vt可以表示为:

Vt=V1t-V2t

(6)

利用式(2)(3)计算出主从动轮齿面的最大最小曲率半径大小,并将其作为圆柱滚子曲率半径的确定依据。利用式(4)—(6)计算出最大齿面切向速度和相对滑移速度作为圆柱滚子模型中滚子转速的确定依据。

此外,圆柱滚子的垂直载荷大小应当与航空高速重载直齿圆柱齿轮的齿面法向载荷相对应。直齿圆柱齿轮齿轮从动轮齿受力分析如图3所示,其中d2为从动轮分度圆直径,T为扭矩。为了计算图3中的齿面名义法向载荷Fn,将其在分度圆处分解为圆周力Ft和径向力Fr,根据力平衡条件和各力之间的几何关系,齿面名义法向载荷Fn可以表示为[14]:

(7)

式中:rb2为从动轮基圆半径;P为从动轮输出功率,kW。

图3 直齿圆柱齿轮轮齿受力分析

根据式(7)可以求出齿面法向载荷的大小,并将其作为圆柱滚子模型中滚子垂直载荷的确定依据。

3 建模与仿真分析

以某在研航空发动机齿轮箱为研究对象,根据式(2)—(7)分别计算得出齿轮箱中所有直齿圆柱齿轮的齿面曲率半径、齿面切向速度、齿面相对滑移速度以及齿面载荷,并最终总结得出的航空发动机高速重载齿轮齿面曲率半径、齿面切向速度、齿面相对滑移速度以及齿面载荷的大致范围如表1所示。基于此范围确定圆柱滚子的曲率、转速以及载荷等参数大小。

由于相对滑移速度的大小随着两接触面的切向速度变化而变化,所以为了定量分析齿面切向速度对主从轮齿接触的影响,保持圆柱滚子接触面之间的相对滑移速度Vt为20 m/s。直齿圆柱齿轮理想润滑条件下的齿面摩擦系数为0.01～0.02[15],所以滚子之间的接触摩擦系数固定为0.01。

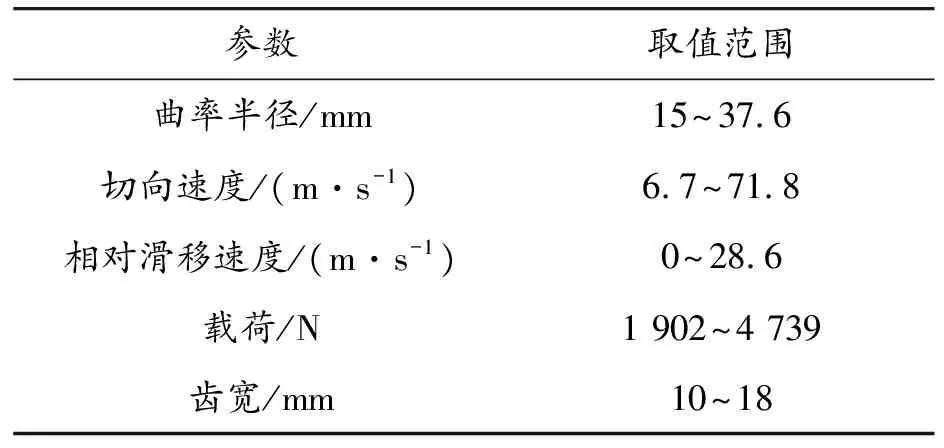
表1 航空发动机高速重载齿轮齿面曲率、速度和载荷等参数范围

分别建立4组接触面切向速度不同的圆柱滚子曲面接触模型,具体参数如表2所示。

表2 圆柱滚子曲面接触模型参数

图4为圆柱滚子曲面接触有限元模型。分别对上下滚子施加大小不同的转速,并在上滚子轴心线的节点上施加竖直向下的均布载荷,最后在上下滚子的接触面之间建立接触。

图4 圆柱滚子曲面接触有限元模型

将模型导入ANSYS软件中使用LS-DYNA求解器仿真计算。对于线速度大于20 m/s的航空发动机直齿圆柱齿轮,单对轮齿的啮合时间往往不超过0.001 s,所以将两圆柱滚子在0.001 s时间内接触产生的滑移能仿真值与理论值之间的百分比误差小于10%作为前提,对比分析得出在不同切向速度下曲面网格尺寸大小与曲率半径之间的最佳倍数关系。

图5分别为表2中4组圆柱滚子曲面接触模型在0.000 2、0.000 4、0.000 6、0.000 8、0.001 s时的滑移能损失误差曲线。

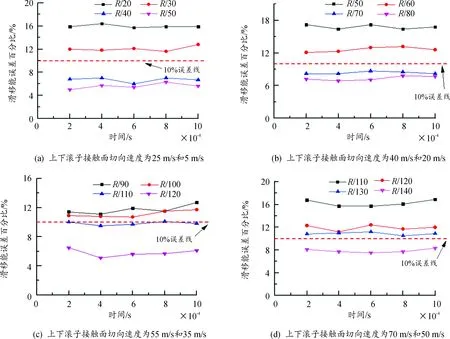
图5 不同切向速度下的圆柱滚子滑移能误差曲线

根据以上仿真结果可知,随着网格的细化,滑移能误差百分比值呈现逐渐减小的趋势,而随着时间的推移,滑移能仿真值与理论值之间百分比误差维持在小范围内波动,基本保持恒定。同时,在相同的网格细化程度下,滑移能误差百分比与2个滚子接触曲面之间最大切向速度的绝对值成正比关系,最大切向速度越大,则滑移能误差百分比值越大。对于最大切向速度为25 m/s的滚子模型,接触面网格尺寸为R/40～R/50时的滑移能百分比误差相对较小,满足建模精度要求。最大切向速度为40 m/s时,接触面网格尺寸为R/70～R/80时的滑移能百分比误差小于10%。最大切向速度为55 m/s时,接触面网格的细化程度最少要达到R/110才能达到建模精度要求。而当最大切向速度为70 m/s的滚子模型,接触面网格的细化程度至少需要要达到R/140,才满足误差小于10%的工程精度要求。综合误差、齿轮齿面参数以及模型计算时间等多方面因素,总结出满足工程建模精度的高速齿轮齿面网格细化准则,如表3所示。

表3 直齿圆柱齿轮齿面网格尺寸确定标准

4 算例与验证

为了证明上述方法的有效性,以某在研航空发动机齿轮箱中的一对直齿圆柱齿轮副为例,根据表3中给出的齿面网格离散准则划分齿轮齿面有限元网格,并分别建立4组不同转速工况下的齿轮啮合有限元模型,对其进行仿真分析。齿轮基本参数如表4所示。

表4 航空发动机齿轮箱中某直齿圆柱齿轮副参数

利用式(2)(3)可以计算出主从轮齿齿面的最小曲率半径分别为24.7 mm和17.2 mm,利用式(4)—(6)计算出4种转速下齿轮副轮齿啮入到啮出过程中的最大齿面切向速度,并根据表3确定出该齿轮副在4种转速下的最佳齿面有限元网格尺寸,如表5所示。

以表5中的第一组工况为例,说明齿轮副啮合有限元模型的建模方法(其余工况除转速、扭矩及齿面网格尺寸不同外,建模流程均相同)。图6为主从轮齿齿面有限元模型。其中齿面体网格均使用六面体网格,齿廓线上的节点间距以及齿向方向的网格节点间距均等于表5中计算得出的齿面网格尺寸。

表5 不同工况下的最佳齿面有限元网格尺寸

图6 主从轮齿齿面有限元模型

如图7所示,分别以对主从动轮施加转速、转矩及接触为边界条件,建立齿轮副啮合有限元模型。最终导入ANSYS中利用LS-DYNA求解器进行仿真求解。

分别提取齿轮接触力稳定阶段时4种不同转速下节点位置处的齿面接触应力,如图8所示。根据仿真结果可知,主从轮齿齿面接触区的应力呈较为理想的椭圆形分布,表5中工况1、工况2、工况3和工况4所对应的最大齿面接触应力分别为608.6、545.2、597.2和666.5 MPa。

图7 齿轮副啮合有限元模型

图8 4种工况下的齿面接触压应力

参考国家标准[16],齿轮使用系数、齿间载荷分配系数及齿向载荷分布系数均取1,而表5中的工况1、工况2、工况3和工况4所对应的动载系数分别取1.65、1.44、1.21和1.06,根据赫兹公式计算得出的最大齿面接触应力理论值分别为557.8、597.3、662.9和706.5 MPa,与仿真值之间的误差分别为9.1%、8.7%、9.9%和5.6%。说明上述高速直齿圆柱齿轮齿面有限元网格离散方法能保证不同转速下的齿轮有限元仿真误差小于10%。

同理,相比于表5中的齿面网格尺寸,在工况1的条件下,分别采用一组更大(主从动轮齿面网格尺寸为0.35 mm)和一组更小(主从动轮齿面网格尺寸分别为0.095 mm)的网格尺寸对齿面进行离散,并采用相同的建模方法建立齿轮啮合有限元模型,并对其仿真分析。分别提取2种不同齿面网格尺寸下节点位置处的齿面接触压应力,如图9所示。根据仿真结果可知,大网格条件下所对应的最大齿面接触应力为340.5 MPa,与理论值之间的误差为39%,仿真精度明显变差;而小网格条件下所对应的最大齿面接触应力为541.3 MPa,与理论值之间的误差为3%,仿真精度有所提高。如图10所示,对比3种网格尺寸下的仿真误差及仿真时间可知,齿面网格尺寸越小,有限元仿真精度越高,但同时仿真时间也会大幅延长。说明采用表3所推荐的齿面网格尺寸,既保证了齿轮有限元仿真的精度,也将仿真时长控制在了可接受范围之内,证明上述高线速直齿圆柱齿轮齿面有限元网格离散方法是正确有效的。