实时性改进LTV-MPC的车辆稳定性控制研究
2023-04-11曾兆枫焦恒超舒红宇
曾兆枫,焦恒超,晋 静,舒红宇
(重庆大学 机械与运载工程学院, 重庆 400044)
车辆稳定性控制是车辆主动安全控制技术中的重要部分,可以通过主动前轮转向(active front-wheel steering,AFS)和直接横摆力矩控制(direct yaw-moment control,DYC)来实现[1-3]。分布式电动汽车具有传动链短且各轮单独可控等优势,为车辆稳定性控制系统执行器的灵活快速响应提供了硬件基础,目前已经引起了学者们的广泛关注[4-5],但更多的控制自由度却使控制器计算负担进一步增加,这对控制系统算法的实时性提出了更大的挑战。
车辆稳定性控制系统是一个高自由度非线性约束系统,对实时性有很高的要求。MPC能够处理多目标优化、多约束问题[6],在结构更为灵活的分布式电动汽车控制系统上体现出了更大的优势,其前馈—反馈的结构特点,能够基于系统状态对未来一段时间内的系统状态进行预测,并且采用滚动时域优化的方法,能及时校正控制过程中出现的各种复杂情况。然而MPC需要不断地在线求解优化问题,控制器计算负担较大,特别是传统非线性模型预测控制(NMPC)求解过程复杂、实时性差[7],故将其应用于车辆稳定性控制系统需要对实时性加以改进。文献[8]采用车辆二自由度模型,并用2条直线来拟合非线性轮胎模型的线性区与饱和区来设计MPC控制器,该方法虽然简化了系统模型,但轮胎模型误差较大,控制效果不佳。文献[9]则是在保留轮胎非线性特性的同时对轮胎力进行形式上的局部线性化,提出一种基于非线性车辆模型的LTV-MPC方法。文献[10]在文献[9]的基础上加以改进,提高了轮胎力的局部线性化精度,但没有对其实时性加以改进,反而增加了控制器的计算负担。文献[11]引入微分平坦度(differential flatness)条件,将问题转换为可以很好表现系统非线性特性的Brunovsky标准型,以改善常规方法中线性化过程的误差积累,有效降低了系统的计算负担。文献[12]在算法上对MPC进行了改进,将非线性规划问题转化为代数方程组进行求解,有效提高了系统实时性,为优化算法提供了一种新的思路。文献[13]则采用分层控制的思路,上层控制器计算理想横摆力矩与理想质心侧偏角,将力矩分配交给下层处理,分层结构能减少上层控制器的输出变量个数,简化计算过程。综上所述,基于MPC的车辆稳定性控制系统还存在预测精度和控制实时性的问题,还有待进一步改进和完善。
本文以分布式电动汽车为研究对象,采用分层控制策略,在LTV-MPC算法的基础上进行实时性改进,提出一种实时性横向稳定控制算法。不同于罚函数法的无约束化过程,本文将不等式约束体现在目标函数的惩罚项中,构造随系统状态变化而变化的时变权重矩阵来实现目标函数求解形式上的“无约束”化,从而参照无约束问题的求解过程对其进行直接求解,此方法可以省去复杂的迭代寻优过程,进一步提高控制系统的实时性。最后通过Carsim与Simulink联合仿真实验验证所提出的控制算法的有效性。
1 车辆动力学模型
本文重点研究车辆在转弯工况下的横向稳定性,故忽略车辆的侧倾运动、俯仰运动以及垂向运动,选用考虑到轮胎非线性特性的整车非线性2自由度模型来描述车辆的动力学特性,如图1所示。以简化模型来表征系统动力特征是提高实时性的有效措施之一。
考虑到前轮转角δf较小,近似认为cosδf=1,车辆的侧向和横摆运动的动力学方程表示为:
(1)
式中:m为整车质量;vx为车辆纵向速度;β为质心侧偏角;ωr为车辆横摆角速度;Fyf和Fyr分别为车辆前轴和后轴所受的侧向力;Iz为整车绕Z轴的转动惯量;a和b分别为车辆质心至前、后轴的距离;ΔM为由4个车轮纵向力差所产生的附加横摆力矩,为:
ΔM=c(Fx2-Fx1)+d(Fx4-Fx3)
(2)
式中:c和d分别为前后轮轮距的1/2;Fxi(i=1,2,3,4)表示轮胎所受纵向力,下标1~4分别对应左前轮、右前轮、左后轮和右后轮。

图1 整车2自由度模型示意图
在极端工况下轮胎力处于非线性区,侧向力接近饱和极限,车辆可能出现失稳的情况。若选用线性二自由度模型中的线性轮胎模型来设计控制器则不能表征轮胎的非线性特性,导致计算所得轮胎力与实际轮胎力误差很大,控制效果不佳。故本文选用可以准确反映轮胎非线性力学特征的魔术轮胎公式,并考虑到路面附着系数对轮胎力的影响,侧向力为:
Fy=μDsin(Carctan(Bα-E(Bα-arctan(Bα))))

(3)
式中:α为轮胎侧偏角;B为刚度因子;C为形状因子;D为峰值因子;E为曲率因子。本文参考文献[9]来设置仿真模型的魔术轮胎参数,ai(i=0,1,2,3,4,5,6),取值如表1所示。

表1 魔术轮胎公式相关参数
前后轮纵向力Fzf、Fzr表示为:
(4)
前后轮侧偏角αf、αr表示为:

(5)
2 基于LTV-MPC的实时性改进控制器
本文设计的控制器采用分层控制策略,并重点对上层MPC算法进行实时性改进研究,上层逻辑结构如图2所示。分层式控制器将ΔM和δf作为上层控制器的优化目标,之后将上层预测得到的最优控制序列传递给下层,下层进一步将力矩优化分配到各执行器[14]。整体式控制器则直接以各执行器的执行量作为优化目标,输出参数较多,控制器计算负担较大[15]。故选用分层控制结构可以有效减少上层MPC控制器的输出变量个数,降低控制器的计算负担,有助于提高系统实时性。
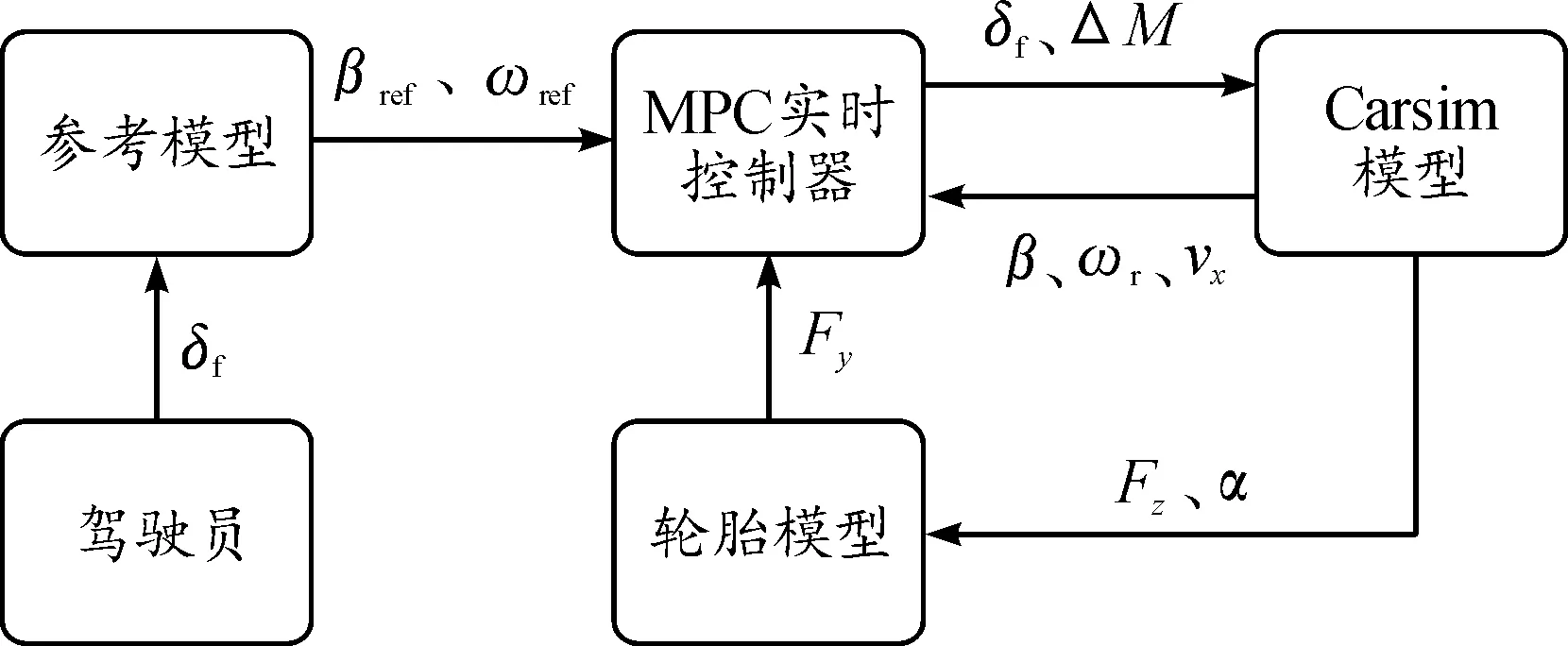
图2 上层控制器逻辑结构框图
2.1 参考模型
本文选用质心侧偏角和横摆角速度作为评价车辆横向稳定性的指标[16],质心侧偏角可以反映车辆跟踪轨迹的能力,横摆角速度则可以反映车辆稳定行驶的能力。参考模型以驾驶员方向盘转角信号和车辆状态为输入,推算出质心侧偏角和横摆角速度的期望值,参考模型如下[17-18]:
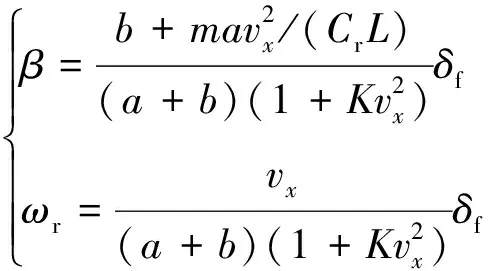
(6)


(7)
2.2 LTV-MPC控制器
魔术轮胎公式虽然能够很好地反映轮胎模型的非线性特性、更好地跟踪实际的轮胎力,但其形式复杂,若直接用于设计控制器算法设计,则不能得到矩阵形式的状态方程,导致控制器过于复杂、计算时间长、实时性较差。想要将非线性轮胎模型应用于实时性更好的LTV-MPC控制器,需要对轮胎力进行线性化。本文在魔术轮胎模型的基础上,针对轮胎侧向力采用一种局部线性化的方式[19],在保留轮胎模型非线性特性的同时将其转化为一种线性表达形式,线性化侧向力方程如下:

(8)

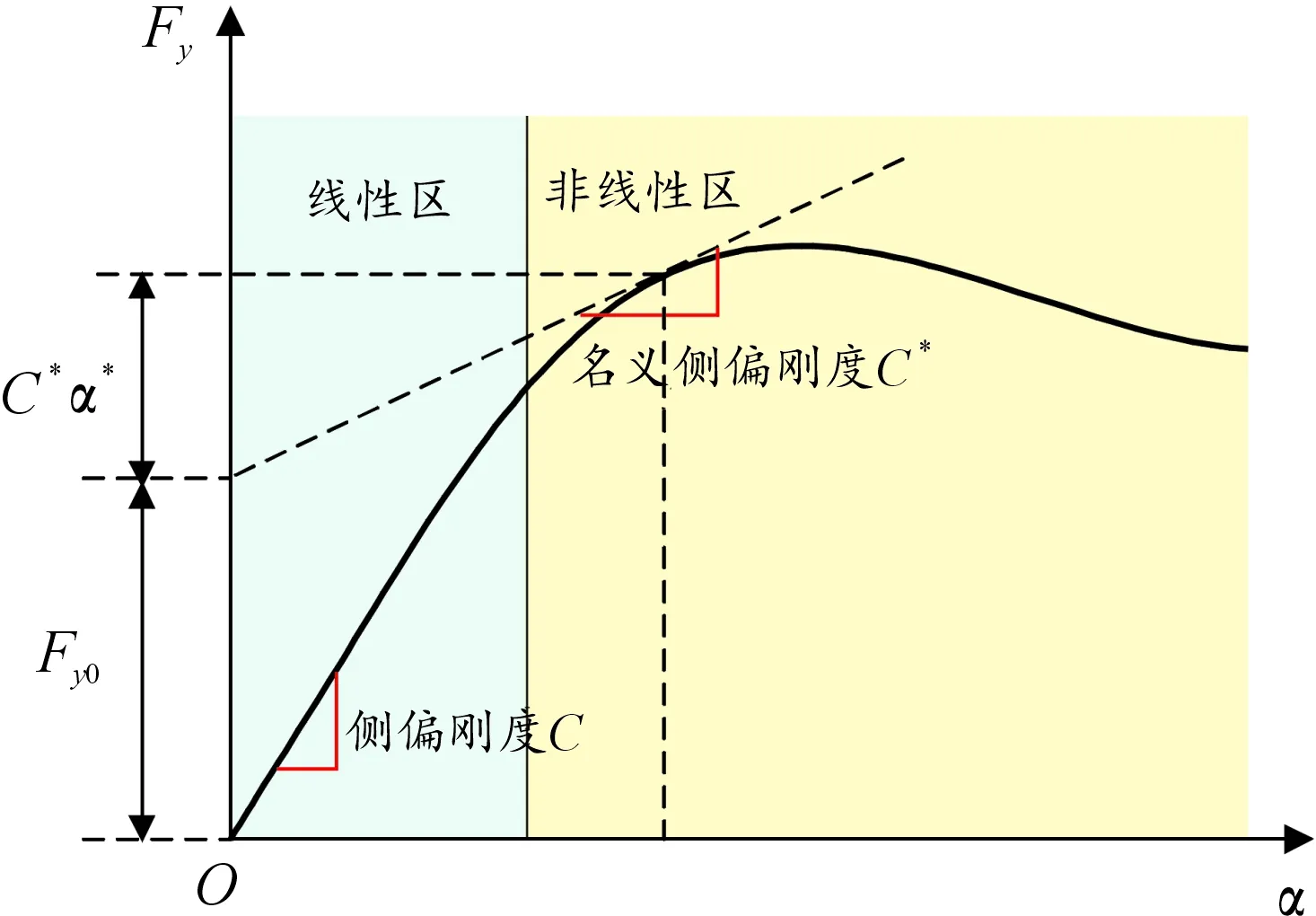
图3 轮胎力局部线性化原理

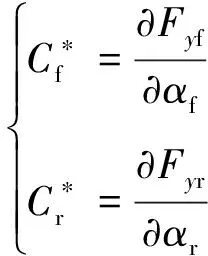
(9)
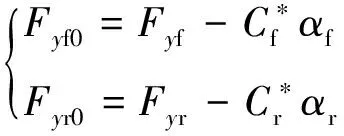
(10)


(11)
式中,各矩阵如下:
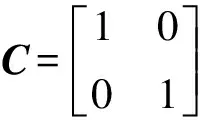
取离散时间步长为Ts,采用单步欧拉法对式(11)其进行离散化处理得到:
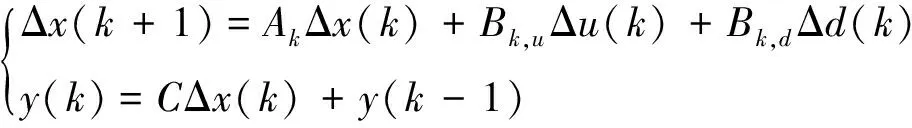
(12)
式中:
Δx(k)=x(k)-x(k-1)
Δu(k)=u(k)-u(k-1)
Δd(k)=d(k)-d(k-1)
Ak=TsA+I,Bk,u=TsBu,Bk,d=TsBd
根据系统当前观测状态来预测系统未来一段时间内的状态是MPC的基本思想,设定预测时域Hp小于控制时域Hc,且控制时域外的控制输入保持不变,即:
全面原则是指网络监测系统对网络信息数据的抓取要尽量全覆盖,全面监测门户网站、博客、论坛、微博等网络载体,不遗漏重要的舆情数据。准确原则是指网络监测系统能够对庞杂的数据进行精确分析,将最有价值的舆情数据筛选出来,进行分类展示,凸显关键舆情信息。及时原则是指网络监测系统能够第一时间抓取到网络数据,第一时间对数据进行分析,第一时间呈现给用户,及时发出预警信号。稳定原则是指网络监测系统要采用先进算法,模块组合合理有效,程序运行顺畅,系统易于扩展,数据处理平稳可靠。
Δu(k+Hc+i)=0,
i=0,1,…,k+Hp-Hc
(13)
基于该假设,可求得预测时域内系统的预测输出:
Y(k+1|k)=SxΔx(k)+SuΔU(k)+
SdΔd(k)+Syy(k)
(14)
式中,k+1|k表示在k时刻对k+1时刻的预测,各矩阵如下:
2.3 实时性改进目标函数设计
构造目标函数时不仅要考虑到控制器对目标输出的跟踪效果,还需要考虑到控制量的波动以及系统的约束限制。通常将约束优化问题转化为QP问题来进行求解,目标函数可表示为:
(15)
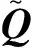
minJ(x(k),u(k))
s.t.δf min<δf<δf max
ΔMmin<ΔM<ΔMmax
(16)

(17)
目标函数(15)改写为:
J=ρTρ
(18)
将式(14)代入式(17)可得:
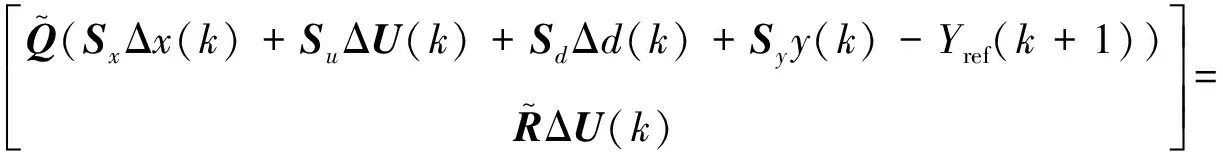
(19)
其中:

(20)
进而,待求解的无约束优化问题可简化为:

(21)

z*=(ATA)-1ATb
(22)
即k时刻的最优控制序列为:
(23)
通过式(23)即可直接求解无约束问题最优解,省去了繁琐的迭代寻优过程,仅需对式中参数进行实施更新便可直接求得最优控制序列,具有很好的实时性。但对于车辆控制系统来说,约束条件是必须要考虑的因素。传统罚函数法是在目标函数后边加上一项约束条件相关的惩罚项,从而将约束问题转换为无约束问题, 针对本文优化问题,则是在目标函数(15)后边加一项关于u(k)的惩罚项。罚函数法虽然能将约束问题转化为无约束问题,但所得到的新目标函数不能转换为类似式(23)所示的解析式,复杂的求解过程依然面临实时性问题。
本文受无约束优化问题求解过程的启发,构造一种能体现系统约束的时变权重矩阵对控制量增量进行惩罚约束,核心思想是通过对控制量增量的约束来实现对控制量的约束,这样即可在不破坏目标函数结构形式的情况下实现优化求解形式上的无约束化,新的目标函数形式如式(24)所示,式中ΓU为关于控制量的时变函数。在整车控制过程中,控制器响应频率高,短时间来看系统状态是渐变的,故本文设置了一个控制量的约束带,将控制过程中控制量所在的区域分为约束区和无约束区,如图4所示。

图4 改进算法原理示意图
当控制量处于无约束区时,认为控制量短时间内不超过实际约束极限,此时不需要对系统加以约束条件限制,Γu不起作用。控制量一旦进入约束区Γu便开始起作用,如图4中的t1时刻。依据在未来时刻施加相同的控制量增量的情况下,当前时刻的控制量越接近系统约束极限,未来时刻的控制量就越容易超过系统约束的基本思想,从约束下界us开始到约束上界ue,应对Δu的限制力度逐渐增大,且在约束上界处达到最大,如图中t2时刻。当控制量欲超过ue时,Γu对Δu的惩罚限制维持在最大值,使得u不超过约束上界,直到u有下降的趋势,在图中t3时刻控制量再次进入无约束区。在极限工况下,此方法求解的并不是问题的最优解,而是牺牲一部分控制精度来提高系统运算速度,得到一个次优解。但因为MPC滚动优化的特性,控制系统会对车辆状态不断地进行优化调整,在整个控制过程中出现一部分次优解依然能够保证控制系统具有一个良好的控制效果。
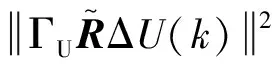
(24)
在k时刻对系统k+1时刻进行预测时,ΓU应该为U(k+1)的函数,但考虑到U(k+1)=U(k)+ΔU(k),在k时刻,U(k)为已知量,ΔU(k)目标函数最优解,故ΓU本质上是关于ΔU(k)的函数。但在k时刻ΔU(k)是未知量,不能对目标函数式(24)进行简化直接求解。为解决此问题,本文采用U(k+1)的估计值来构造ΓU。鉴于在求解k时刻的优化控制序列ΔU(k)时,k-1时刻的优化控制序列来ΔU(k-1)是已知量,故设想采用ΔU(k-1)来预测ΔU(k),因此本文设置实验对此设想进行检验。因为MPC在控制过程中每一时刻只将控制序列的第一项施加于系统,所以重点对优化结果中控制序列的第一项进行观察。k时刻施加的控制量Δu(k+1|k)对应k-1时刻控制序列中的第二项Δu(k+1|k-1),若两者变化趋势相近且对应数值差异不大,便可将Δu(k+1|k-1)作为Δu(k+1|k)的预测值。利用Carsim与Simulink联合仿真平台进行实验,设置在平坦路面上,对方向盘进行120°正弦转角输入,在无加速无制动的情况下,分别以初速72 km/h,路面附着系数0.8(工况1)、初速72 km/h,路面附着系数0.4(工况2)2种工况对控制过程中的Δu(k+1|k)与Δu(k+1|k-1)进行观察,观察结果如图5(a)、(b)、(c)、(d)所示。


(25)

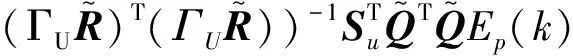
(26)

(27)
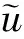

图5 不同工况下控制增量曲线
3 仿真分析
为了验证本文提出的实时性改进MPC控制器的有效性,采用Carsim与Simulink联合仿真平台搭建模型对其进行仿真验证。设置初始车速为72 km/h、方向盘如图6所示施加120°正弦转角输入、纯滑移,分别在路面附着系数为0.8和0.4的2种路面上进行实验,并设置LTV-MPC控制器作为对照。车辆参数如表2所示,控制器参数如表3所示。
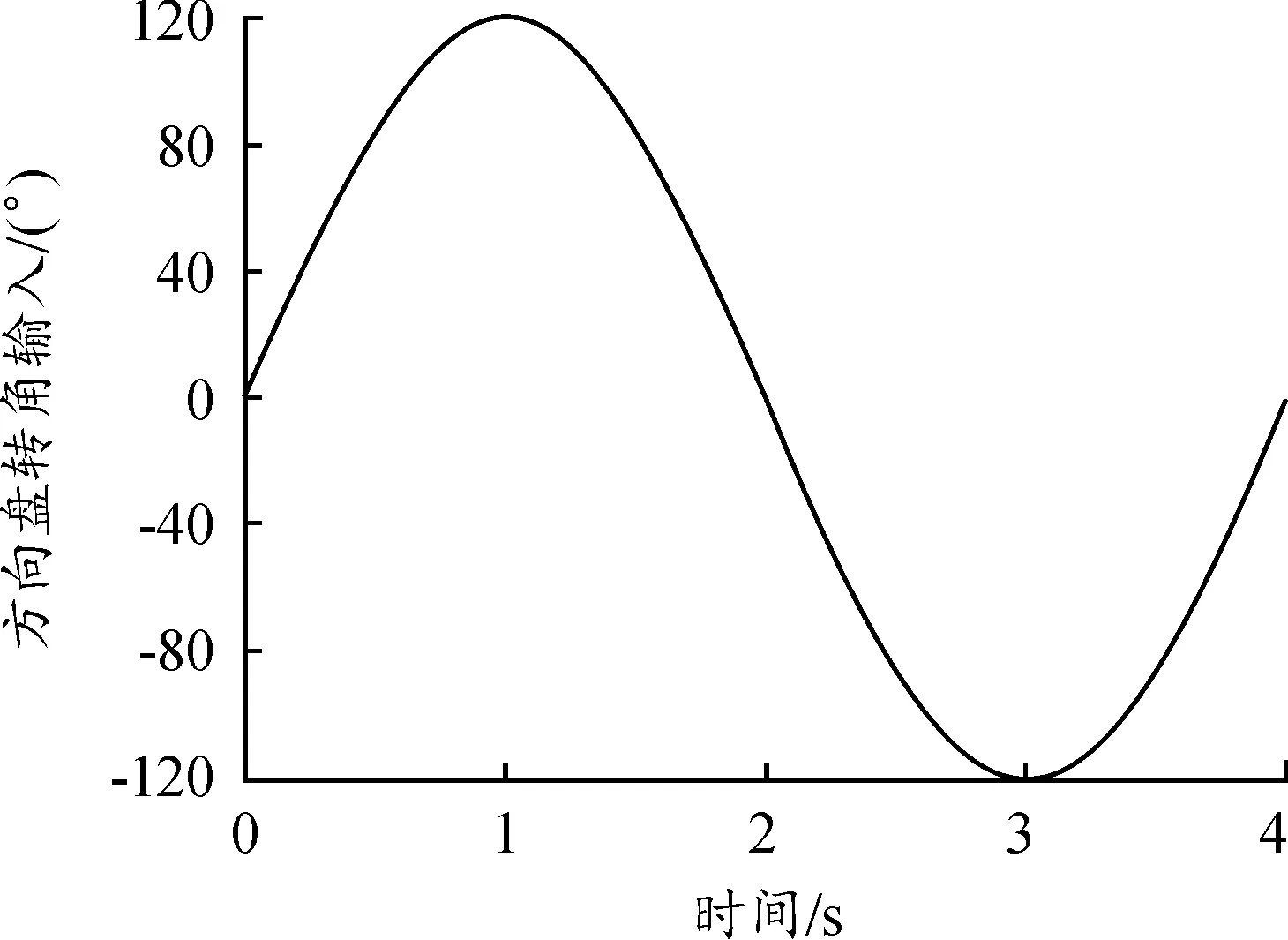
图6 方向盘转角输入

表2 车辆参数

表3 控制器参数
在本文中,设置-0.3 rad<δf<0.3 rad、-2 000 N·m<ΔM<2 000 N·m作为LTV-MPC控制器的系统约束以及改进算法的软约束边界。图7为高路面附着系数(u=0.8)工况下控制器的响应曲线,图8为低路面附着系数(u=0.4)工况下控制器的响应曲线。其中图7(a)和图8(a)为横摆角速度响应曲线,图7(b)和图8(b)为质心侧偏角响应曲线。从图中可以看出,在控制效果方面,本文提出的改进算法在高低附着系数工况下对横摆角速度都有很好的跟踪效果。虽然在控制过程中改进算法相较于LTV-MPC波动较大,但也能很好地跟踪期望值,控制效果良好。实际质心侧偏角与期望值有一定的差异,高路面附着系数下差异较小,低路面附着系数下差异较大。在控制算法中,目标函数权重系数是影响控制效果的关键,而横摆角与质心侧偏角存在着一定的耦合关系,在严格跟踪横摆角速度的同时会对质心侧偏角有一定的制约,导致质心侧偏角与目标值存在一定的差异,如文献[10]中的LTI-MPC控制器是以牺牲横摆角速度的跟踪性能为代价,使得质心侧偏角与期望值的变化差异最小。

图7 高路面附着系数控制器响应

图8 低路面附着系数控制器响应
本文以保证车辆稳定行驶的横摆角速度作为跟踪重点来设置权重系数,故相比于横摆角速度,质心侧偏角与期望值的差异较大,但其变化趋势与期望值一致,并且大部分时刻其实际值小于期望值,实际行驶路径不会与理想路径产生太大的偏差,即在实际控制过程中能保证车辆稳定运行。
为验证改进算法的实时性改进效果,对控制器单次预测运算时间进行对比,仿真实验软硬件配置如表4所示。图9为改进MPC与LTV-MPC控制器在每一个采样时刻进行单次预测的计算时间对比,可以看出采用QP迭代寻优的LTV-MPC控制器计算时间在0.02~0.034 s浮动,而采用解析求解的改进MPC计算时间基本稳定在 0.004 5 s。与LTV-MPC控制器相比,本文提出的改进MPC控制器计算速度提高了4.5~7.5倍,并且计算时间波动较小,有效改善了控制系统的实时性。

表4 仿真软硬件配置

图9 控制器计算时间曲线
4 结论
基于MPC车辆稳定性控制系统的实时性,在LTV-MPC的基础上,在考虑系统的非线性特性前提下,进一步提出了通过时变权重矩阵实现了约束优化问题形式上的无约束化的方法。基于Carsim与Simulink联合仿真试验和分析,验证了该算法可以显著节省计算时间,与LTV-MPC控制器进行对比,求解速度可提高4.5~7.5倍,有效地改进了控制算法的实时性。该方法还有待通过实车实验和车载控制器验证其实际效果。
