具有紧急制动功能的多模式自适应巡航控制策略
2023-04-11林嘉玉杨鄂川韩先胜
欧 健,黄 栋,林嘉玉,杨鄂川,韩先胜
(1.重庆理工大学 车辆工程学院, 重庆 400054;2.重庆工贸职业技术学院 车辆工程学院, 重庆 408000;3.重庆理工大学 机械工程学院, 重庆 400054)
近年来,汽车的保有量逐年增加,据国家公安部统计[1],截至2021年底机动车保有量达3.95亿辆。为了提高驾驶员的行车安全性和便捷性,全世界各汽车行业都在开发高级驾驶辅助系统(advanced driving assistance system,ADAS),特别是自适应巡航控制的研究与开发备受关注[2]。
ACC控制结构会影响到控制器运行的整体效率,通常采用分层设计,包括上、下层控制器[3-5],其中上层控制器将传感器检测到的车辆信息,通过合适的控制方法,输出期望加速度;下层控制器则将上层的输出转化为节气门开度(驱动转矩)和制动压力,从而达到控制目标。针对控制器控制算法,国内外研究人员都做了大量的研究。清华大学的李升波等[6]总结到,目前已有多种算法被用于设计上层控制器:PD反馈控制器、模型预测控制(model predictive control,MPC)、滑模控制(sliding mode control,SMC)、最优控制(linear quadratic regulator,LQR)、线性变参数、强化学习等。下层控制器的设计也是ACC系统中的重要环节。其中,动力总成、制动系统模型以及驱动/制动间的切换策略是主要研究方向。下层控制器模型主要使用逆模型对上层输出量进行跟踪控制[7-8],文献[9-10]则采用基于阈值的驱动制动模式切换策略。在以上控制算法中,PID[11-12]、LQR[13-14]和MPC[15-16]算法在ACC系统中有着更为普及的研究与应用,然而,相较于传统PID的结构简单且鲁棒性好的优点,MPC则具有预测功能以及动态响应好等优点,且在处理多约束多目标问题上具有较大优势。
目前,合理的切换模式和切换策略对整个ACC系统的实现具有重要意义,但关于这方面的研究相对较少。合肥工业大学的孙晓文等[17]将ACC系统分为巡航速度控制和跟车距离控制2种模式,提出的控制策略能够保证ACC车辆的行车安全,但在车距与车速模式之间切换时,加速度会在短时间内超出期望值,降低了舒适性;吉林大学的高振海等[18]根据自车的加速度将ACC分为巡航、稳态跟随和瞬态跟随模式,但并未充分考虑前车加速度变化对ACC系统的影响;清华大学的王建强等[19]基于零期望加速度曲线,将ACC分为定速巡航、车距保持、接近前车和超车模式,较好地解决了模式切换中的加速度突变问题,但超车模式隶属于驾驶员操作,不应存在于系统自动驾驶模式中;南昌大学的刘明春等[20]将ACC划分为5个控制模式,将跟车模式细分为加速接近、稳态跟车、减速接近与紧急跟车4个模式,但文中并未考虑前方紧急工况与驾驶员特性;中国科学院微电子研究所的章军辉等[21]将ACC系统划分出6种工作模式,同时采用模糊推理与加速度加权平均策略,以实现工作模式最佳匹配与平稳过渡,文中虽考虑了部分驾驶员心理,但采用固定时距会在一定程度上降低车辆对环境的适应性能;北京理工大学的裴晓飞[22]将ACC更加详细地划分为8个模式,在处理纵向前车急加速、急减速与紧急工况中,具有良好的性能,但跟车过程太过详细,反而导致整体控制模式太过繁琐,不利于系统的稳定。
针对现阶段ACC系统切换模式较为简单,且未考虑前方突现静止物的复杂交通状况,将ACC系统划分3种主模式和4种子工况,采用分层控制策略设计ACC控制器,其中,定速巡航模式采用模糊PID进行设计,可根据环境变化动态调整PID参数;跟随模式在充分考虑行驶过程中的跟车性、安全性以及舒适性等指标的前提下,采用MPC算法进行设计与优化;基于电机模型设计下层控制器,并选取最大轮缸压力作为接管模式下的制动压力。最后采用CarSim/Simulink进行联合仿真,验证所设计ACC系统的可行性。
1 ACC框架定义
根据前方车辆是否处于自车巡航间距范围,并考虑到紧急工况,本文基于距离和TTC将ACC模式划分为巡航、跟随和接管3种,为提高该控制器对复杂多变环境的适应能力,通过引入指标参数TTC-1,将跟随模式进一步划分为4种子工况:加速、强减速、弱减速、稳态跟随,并设计基于MPC的多目标ACC控制器;基于模糊PID设计定速巡航模式;通过仿真实验选取特定轮缸压力作为紧急制动压力,用于设计接管模式;最后通过搭建下层控制器和仿真环境形成ACC框架,如图1所示。

图1 ACC总体框架示意图
2 模式切换策略与划分设计
切换条件直接影响到整个模型的运行流畅性与逻辑性。距离和TTC由于计算量低且能减少决策时间,而被用于切换判据。
2.1 安全距离设计
2.1.1巡航距离
当前方无车、距离过远或者前方车辆驶出当前车道时,自车进入定速巡航模式。考虑到控制器对复杂工况的适应能力,选取车头时距和自车车速动态计算巡航间距,公式如下:
S=Thvf+d0
(1)
式中:S为巡航间距;Th为车头时距,一般取值范围为5~8 s,设置6 s作为巡航时距;vf为自车速度;d0为最小固定车间距,设置5 m作为最小车间距。
2.1.2接管距离
当前车紧急减速或者前方车辆掉落的障碍物,且满足切换条件时,自车进入接管模式,本车以设定最大制动轮缸压力进行纵向制动避撞。为了减少计算量,基于制动过程搭建纵向安全距离模型,计算接管间距,因此可得纵向安全距离表达式:
S=Sf+d0-Sd
(2)
考虑到紧急工况,选取前车静止与紧急制动2种工况进行分析。
1) 前车静止工况。
当同一车道前方车辆静止时,自车执行紧急制动,制动过程前车位移Sd=0,自车制动位移为Sf。安全距离模型公式如下:
S=Sf+d0=
(3)
式中:t1为加速度从0到amax所需时间;t2为车速从v0减到0所需时间;v0为自车初始速度;Jmax为车辆制动减速度梯度,取Jmax=21 m·s-3。
2) 前车紧急制动工况。
当同一车道前车紧急制动时,自车也执行紧急制动,以避免碰撞。紧急制动下安全距离公式为:
(4)

2.1.3跟随距离
当车间距处于巡航间距和接管间距之间时,自车进入跟随模式。考虑到前车速度变化会影响车头时距,为了使车间距更加贴合实际工况,设计一种可方便预测的VTH策略,其表达式如下:

(5)
式中:th为车头时距值;t0、cv为大于0的常数,其中t0=1.5 s,cv=0.05;vrel为两车相对速度;th_max、th_min分别为车头时距的上、下限值,其中,th_max=2.2,th_min=0.2;ca为大于0的常数,其中ca=0.3;ap为前车加速度。
结合可变车头时距,可得期望跟车间距如下:
S=thv+d0
(6)
2.2 子模式划分策略设计
跟随模式主要针对安全距离下的稳态跟随、加速、强减速、弱减速等工况,因此需对子工况进行划分。基于TTC-1设计子模式,定义如下:
(7)
式中:Δv为两车相对速度,Δv=v2-v1,v2为前车车速,v1为自车车速;d为两车车间距。
当TTC-1接近0时,自车越安全,且稳态跟随前车;当v2大于v1时,两车越安全;反之,两车容易发生碰撞。因此将子模式进行详细的划分:
1) 当-0.05≤TTC-1≤0.05时,车辆为稳态跟随工况,加速度范围为-0.6~0.6 m/s2;
2) 当-0.12≤TTC-1≤-0.05时,车辆为弱减速工况,最大减速度约束为-2 m/s2;
3) 当TTC-1≤-0.12时,车辆为强减速工况,最大减速度约束为-5 m/s2;
4) 当TTC-1≥0.05时,车辆为加速工况,加速度约束范围为0.6~3.5 m/s2。
2.3 整体模式切换策略设计
在2.1节的基础上,设计整体模式控制逻辑如图2所示。
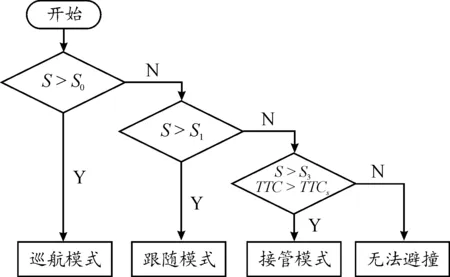
图2 整体模式控制逻辑框图
图2中,S0、S1、S3以及TTCs分别为各种模式的切换条件,其中,定义S0为巡航间距,S1为接管间距,S3为无法避撞间距,TTCs=1.3 s[23],当满足条件时,则进入对应模式,否则继续保持模式不变,其工作流程如下:
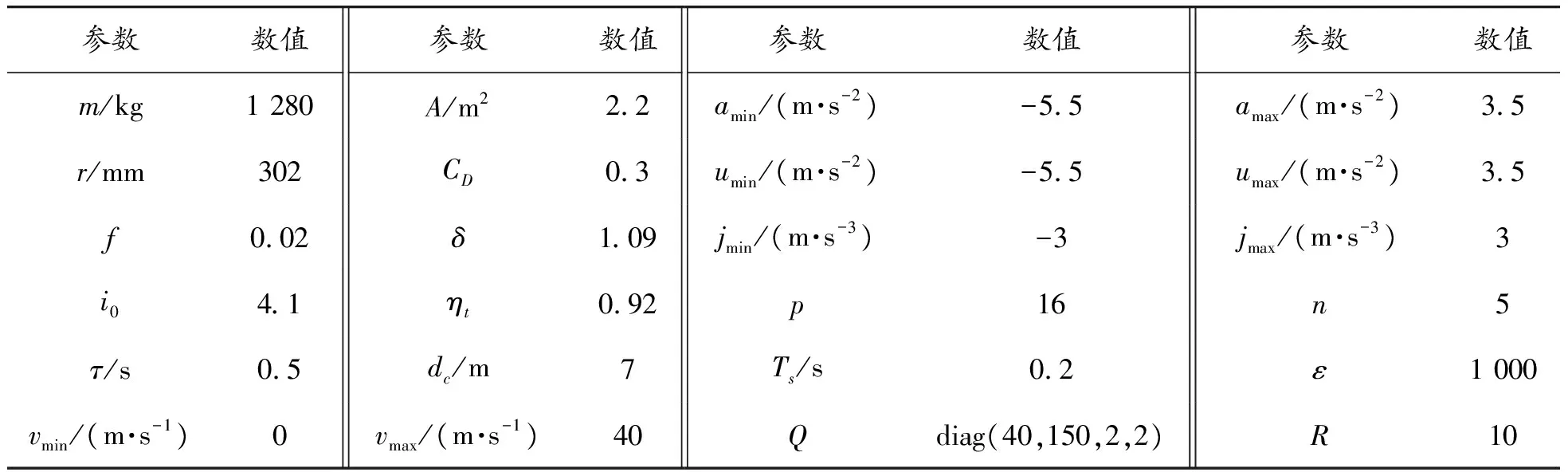
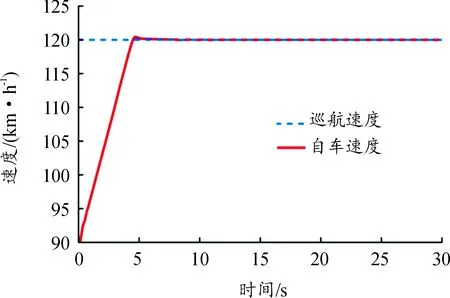
1) 当S0 2) 当S1 3) 当S3 3.1.1定速巡航模式设计 PID控制是通过输入当前状态值与设定值之间的误差,计算变量输出,其形式为: (8) 式中:u(t)为控制器的输出变量;e(t)为当前值与设定值之间的误差;kp、ki和kd分别为比例系数、积分系数和微分系数。 设定模糊PID控制器的输入为当前速度与巡航速度的差值e,以及差值的变化率ec,输出为车辆的期望加速度ades;E、Ec、Kp、Ki、Kd分别为e、ec、kp、ki、kd所对应的模糊值。定义e的基本论域为[-90,90],ec的基本论域为[-8.33,3.5];增益kp的基本论域为[1,10];增益ki的基本论域为[0.001,0.01];增益kd的基本论域为[0,2]。模糊变量均设定7个模糊集:负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)。选用三角函数描述模糊输入变量,如图3所示,输出变量与输入变量隶属度一致,不再赘述。 图3 输入变量隶属度函数曲线 为保证曲线上升时间、超调量、稳定时间、稳态误差合理,需调节增益Kp、Ki、Kd,最终建立模糊规则表,如表1所示,并在Matlab/Simulink中搭建量化因子与比例因子部分,从而控制车辆快速且舒适地跟踪上巡航车速。 表1 Kp、Ki、Kd模糊推理规则 3.1.2跟随模式设计 跟随模式设计的好坏直接影响整体ACC控制器的性能表现,该模式主要功能是对复杂工况做出快速反应,同时兼顾多个优化目标,基于此,设计基于MPC的多目标ACC控制器。 1) 纵向动力学模型设计。 通过分析两车间运动学关系,如图4所示,考虑到自车加速度与加速度变化率,可得自车与前车的运动学公式如下: (9) 式中:Δx为实际车间距;ap为前车加速度;a为自车加速度;v为自车车速;vrel为相对车速;u为期望加速度;j为自车加速度变化率;Ts为采样时间;τ为下层控制器控制时间。 图4 两车运动学关系示意图 选取两车车间距、自车车速、相对车速、自车加速度和自车加速度变化率作为ACC控制系统的状态量[24],即x(k)= [Δx(k),v(k),vrel(k),a(k),j(k)]T。定义x为自车位置,选择w作为系统干扰量,选取y(k)=[δ(k),vrel(k),a(k),j(k)]T作为待优化目标,整理得到纵向运动学状态方程模型: (10) 式中: 式中,th为可变车头时距。 文中引入指数衰减函数作为优化目标的参考轨迹,例如,两车车间距的参考轨迹如下: δref(k+i)=δ(k)+ (11) 式中:δref为车间距误差的参考轨迹;αδ为该参考轨迹的时间常数;同理,相对速度、自车加速度与自车加速度变化率设置同样形式的参考轨迹,将参考轨迹用向量形式表示如下: 每个单元都要有明确目标,特别要突出能力目标。教师要把知识讲授型为主变成知识应用型为主;从以理论思维为主,变成以能力训练为主;从以知识点、定义、语法为载体,变成以完成项目任务为载体;从学生被动听讲,变成学生主动参与课堂,积极参与新知探索;从教师讲解为主,变成由教师积极引导、创造学习的环境条件为主。把课程评价从 “老师讲过”、“老师讲得好”、“老师完成了教学进度”[2]为目的,变成以学生有兴趣、学生的能力明显提高为目的。老师精讲知识,学生强练技能,在技能训练过程中,学生自己学到了知识。 yrel(k+i)=φiy(k) (12) 式中:φ为车间距、相对速度、自车加速度与自车加速度变化率组成的对角矩阵;yrel为优化目标的参考轨迹向量。 2) 控制目的与约束分析。 通过控制两车车间距保证两车安全性,假定xp为前车位置,dc为最小安全间距,其安全性约束如下: xp(k)-x(k)≥dc (13) 车辆间的实际与期望车间距间的误差应保证尽可能地小,且两车在行驶过程中处于相对静止状态,其跟车性约束如下: δ(k)→0,vrel(k)→0 当k→∞ (14) 影响舒适性的主要因素是自车加速度以及加速度变化率jerk2个参数,因此,需要对其进行优化控制,其舒适性约束如下: (15) 此外,还需要对其他状态量进行约束,使求解值在约束下达到最优,因此乘坐舒适性和燃油经济性约束如下: (16) 3) 基于MPC的多目标ACC控制算法设计。 根据式(10),可建立预测时域内的预测方程,定义ex为实际状态量与预测值之间的误差;W(k+p)为p时域内的干扰量集合,且假定每一时刻值相等。整理得到表达式: (17) 增加权重参数Q和R,其中,Q代表跟车性,R代表安全性。整理得到如下函数表达式: (18) 式中:Q=diag(qδ,qv,qa,qj),u(k+i)为k+i采样时刻的加速度控制值。 根据二次规划(quadratic programming,QP)问题的求解规则,整理前述约束条件,得到如下形式: ΩU(k+n)≤T (19) 式中: 其中: 结合式(18)和(19),使用Matlab中积极求解器进行求解,输出控制量序列,取输出序列中的第一个控制量作为下层控制器的输入。 本文采用轮毂电机作为动力源[25],因此,下层控制器便将上层控制器计算得到的期望加速度ades转换为控制整车模型的驱动转矩Tm与轮缸压力Pb。 3.2.1轮毂电机模型 PMSM的数学模型是一个高度复杂的系统,为了使PMSM能更好地工作并施加相关控制,在做一定简化与假设后,建立PMSM的数学模型如下: (20) 式中:Ld和Lq分别为d轴和q轴定子自感系数;id和iq分别为d轴和q轴定子电流;ud和uq分别为d轴和q轴定子端电压;R为定子绕组电阻;ω为转子的电子角速度;ψk为电机定子磁链;Te为电机扭矩;np为极对的数量;J为负载和机械转子的惯性矩;Tl为负载扭矩;B为负载与机械的摩擦系数。 3.2.2车辆驱动模型 为简化车辆行驶过程,在仅考虑纵向阻力下,通过对车辆受力分析,整理得到驱动力矩表达式为: (21) 式中:r为车轮滚动半径;i0为主减速器传动比;ηt为传动系传递效率;CD为空气阻力系数;A为汽车纵向受风面积;v为车速;m为整车质量;f为滚动阻力系数;θ为路面坡度;δ旋转质量换算系数;ades为加速度。 3.2.3车辆制动模型 在制动过程,不考虑加速阻力和驱动力,且假定车辆在平路上行驶,整理可得纵向制动力Fb公式: (22) 在最大纵向制动力Fb约束范围内,车辆的制动力Fb与油压Pb呈线性变化,定义Kb为制动系数[26],Kb=1 286,其表达式如下: (23) 当前车紧急减速时,自车则需比其更大的减速度进行制动,以避免碰撞。在CarSim环境下,选取车速节点80、100、120 km/h作为测试初始车速,然后以特定轮缸压力Pb进行制动,反向得到对应制动减速度ae,如表2所示。经分析对比,最后采用7 MPa作为紧急制动轮缸压力。 表2 各车速、轮缸压力下的制动减速度 3.2.4驱动/制动切换策略 在CarSim软件中进行滑行实验,得到各速度(10~120 km/h)下的加速度阈值a,为保证驱动/制动间的平稳切换,在原曲线基准的上下设置过渡区域Δh,设置Δh=0.1 m/s2,得到驱动/制动切换逻辑。 3.2.5下层控制器控制方法 本文采用简单快捷的PID控制方案设计下层控制器,并在此基础上引入前馈和误差反馈的方式来弥补模型失配的不足,前馈即是通过上层控制器的计算输出作用于ACC车辆的执行机构控制车辆,而误差反馈则是通过实际状态与期望状态的偏差值进行调节,用来补偿线性模型失配带来的控制误差,提升系统的控制精度,利用PID方法使得期望纵向加速度与实际纵向加速度的偏差值迅速收敛为0,实现对ACC车辆的高效控制,运用试凑法,设定PID控制器的控制参数为kp=0.2、ki=1.8。 为了对所设计的模式切换策略以及控制器进行验证,搭建Matlab/Simulink与CarSim联合仿真平台,其仿真参数如表3所示。 表3 主要仿真参数 设置定速巡航、跟随、紧急制动以及混合切换4种工况进行仿真验证,并在CarSim中将前车驾驶设置为驾驶员操作,并应用于所有工况。 4.1.1定速巡航工况 车辆定速巡航时,ACC进入速度控制模式。车辆设置仿真环境如:自车初始车速为90 km/h,巡航车速为120 km/h,且当前车道无前方车辆,其仿真结果如图5和图6所示。 图5 速度变化曲线 图6 加速度变化曲线 从图5中可以看出,当车辆进入巡航模式时,车辆能迅速响应控制器决策,大约在4.8 s时,车速从90 km/h加速至120 km/h,且速度超调量几乎为0,其后车辆以当前设定巡航速度行驶;从图6中可以看出,自车加速度在些许波动后能快速恢复稳定,保证了乘坐舒适性,同时表明控制器具有稳定性。 4.1.2跟随工况 车辆跟随前车行驶时,ACC进入距离控制模式。设置仿真环境如:本车的初始速度为90 km/h,且在0~160 s之间做加速、强减速、弱减速以及稳态行驶动作,两车初始车间距为50 m。其仿真结果如图7—9所示。 图7 速度变化曲线 图8 加速度变化曲线 图9 车间距变化曲线 从图7和图9中可以看出,自车在各种子工况下都能很好地跟随前车速度,且响应迅速,虽存在超调现象,但最终都能稳定跟随前车行驶;在减速期间,自车与前车未发生碰撞,始终保持安全距离行驶;从图8可以看出,自车实际加速度皆在子模式下的加速度约束范围内,整个过程的加速度保持在-5~3.5 m/s2。 4.1.3前车紧急制动工况 当车辆面临紧急工况时,切换至接管模式,ACC进入距离控制模式。设置仿真环境如:自车初始车速为120 km/h,前车初始车速为100 km/h,两车初始车间距为50 m,当车辆行驶到30 s时,前车开始紧急制动约2.7 s,车速降至30 km/h。其仿真结果如图10—12所示。 图10 速度变化曲线 图11 加速度变化曲线 图12 车间距变化曲线 从图10和图11可以看出,在30 s时,前车开始紧急减速行驶,最大减速度为7.2 m/s2,为避免碰撞,自车切换至接管模式,并以7 MPa的制动轮缸压力制动,最大减速度为7.9 m/s2,当控制器判断为非紧急工况时,自车则切换至跟随模式,且切换策略工作流畅,保证了乘员的舒适性;从图12可以看出,在38 s时,两车车间距为6 m,说明两车在紧急工况下仍能保证安全。 4.1.4混合切换工况 为验证所设计切换策略以及控制器,设置混合工况仿真环境如:自车初始车速为70 km/h,前车初始车速为100 km/h,两车初始车间距为40 m;在29 s和63 s时,前车分别切出、切入当前车道,在99 s时,前车在2.7 s内紧急制动至 30 km/h,前车在其他时间段做加速、强减速、弱减速以及稳态行驶。其仿真结果如图13—16所示。 图13 速度变化曲线 图14 加速度变化曲线 图15 车间距变化曲线 图16 Jerk变化曲线 从图13和图14可以看出,在整个仿真过程中,自车速度能很好地跟随前车,且和加速度并未产生不正常突变;在紧急制动过程中,自车能快速反应,最大减速度达7.9 m/s2,在保证安全性的同时,亦能较快吻合前车速度,大部分时间段的减速度均能维持在-5~3.5 m/s2,保证了行驶舒适性;整体模式切换流程从跟随模式至定速巡航模式至跟随模式至接管模式至跟随模式,模式间均能实现稳态切换;从图15中可以看出,在行驶至99 s时,车辆开始紧急制动,最终两车车间距能保持在5.6 m,且未与前车发生碰撞;从图16中可以看出,除了紧急制动工况,其他工况下的jerk基本维持在-3~3 m/s3,再次体现了驾乘舒适性。 本文提出了一种具有紧急制动功能的多模式自适应巡航控制策略。针对目前复杂多变的工况,特别是紧急工况,将整体控制模式划分为巡航、跟随和接管3种模式,并将跟随模式下的工况进行了更加详细的划分;同时,对3种模式进行了详细设计;多种仿真工况结果表明,所设计的ACC控制器能快速且稳定地跟踪前车速度或巡航速度,模糊PID控制下的速度几乎无超调,MPC控制能保持在10 km/h以内,且迅速恢复稳定;除紧急工况,其他情况下的加速度均能保持在-5~3.5 m/s2;在紧急工况下,自车与前车最终能保持5.5 m左右的车间距,其他工况下的车间距可根据相对速度以及加速度参数动态调整;且所有控制模式可根据复杂多变的工况进行快速平稳切换。 所设计的ACC控制策略满足跟随性、安全性、舒适性以及适应性的要求,且切换模式有效平稳,在紧急工况下能通过纵向避撞策略实现紧急避撞。本文不足之处为在研究过程中未考虑不同驾驶员的驾驶特性以及换道工况等,且仅采用了联合仿真进行验证,后续还需进一步研究与进行硬件在环验证。3 ACC分层控制设计
3.1 上层控制器设计
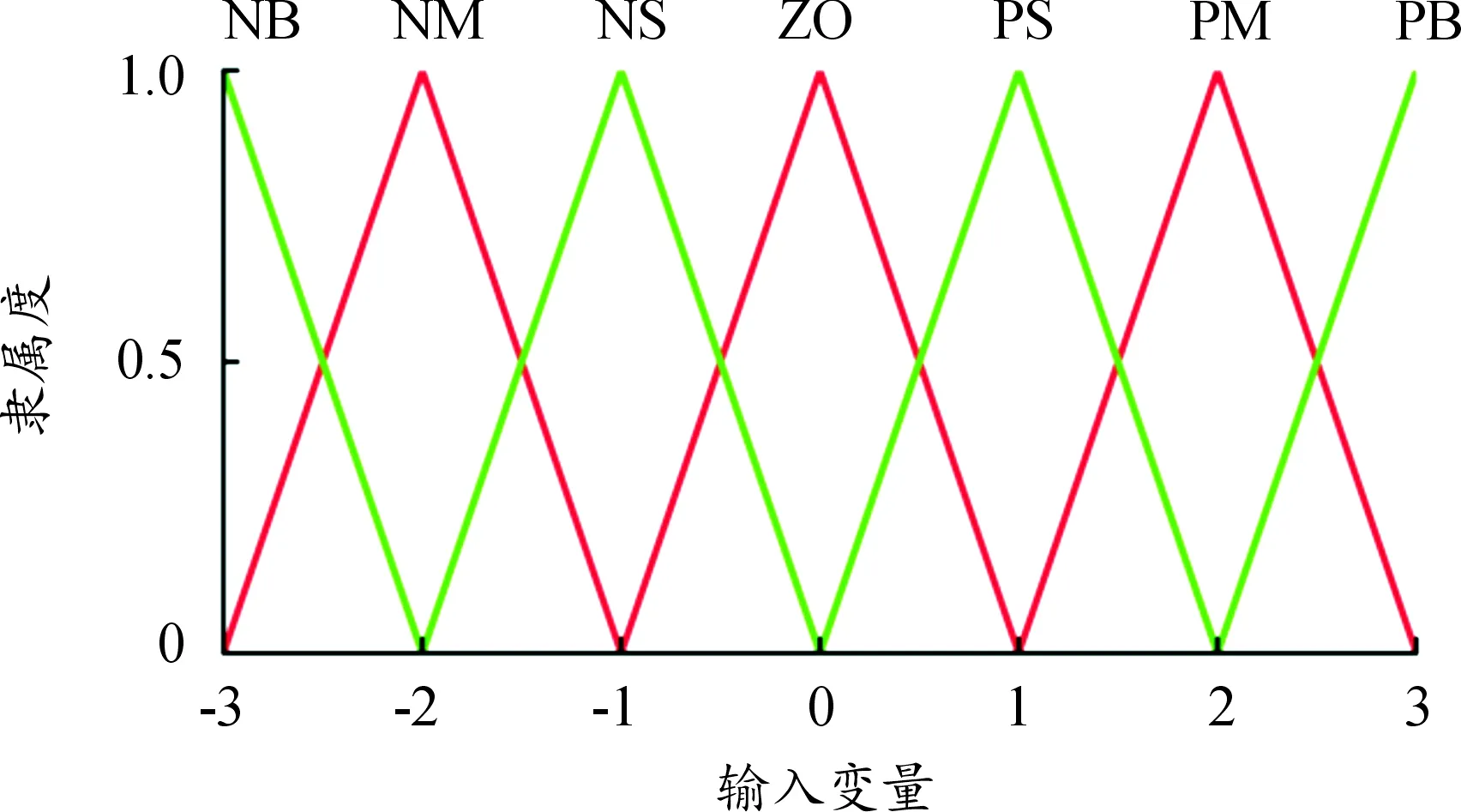
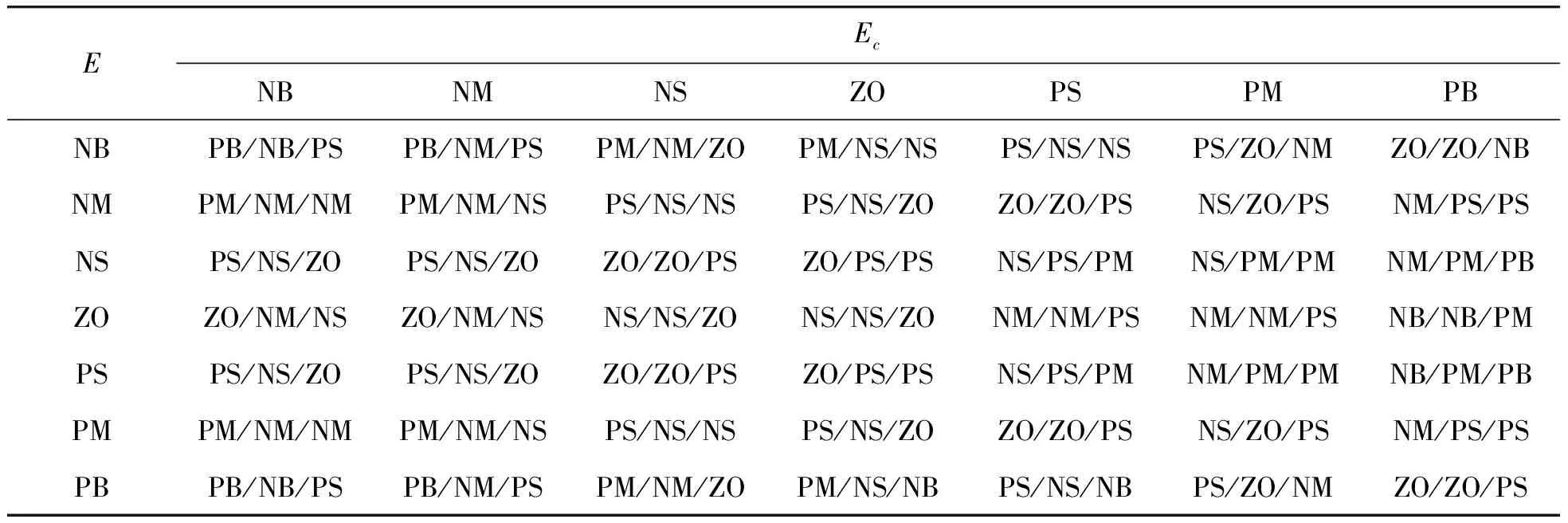

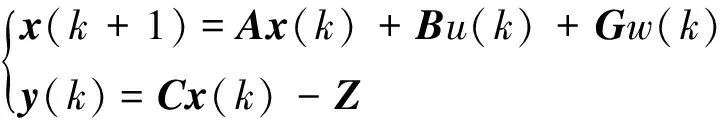
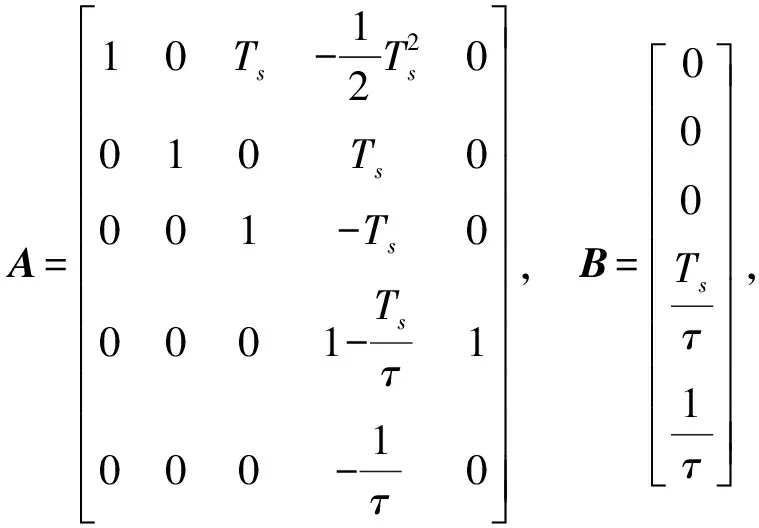

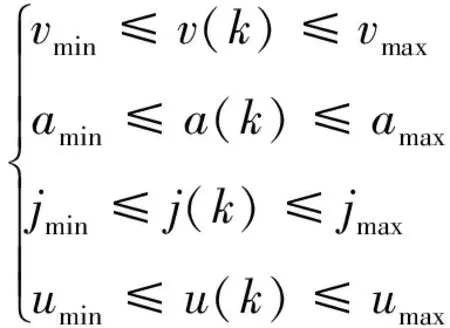
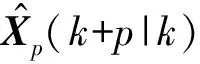
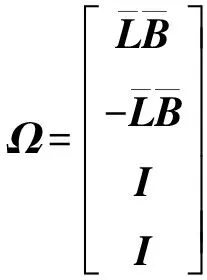
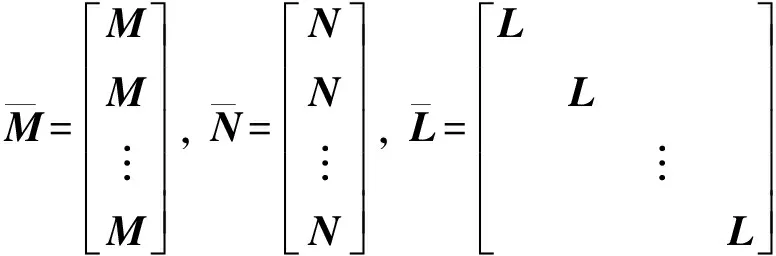
3.2 下层控制器设计
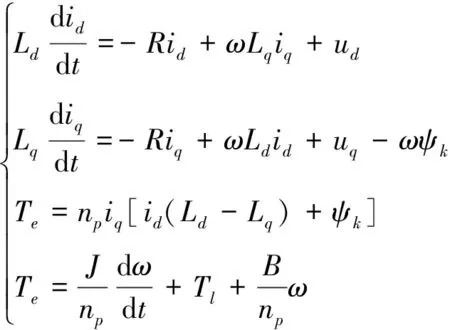

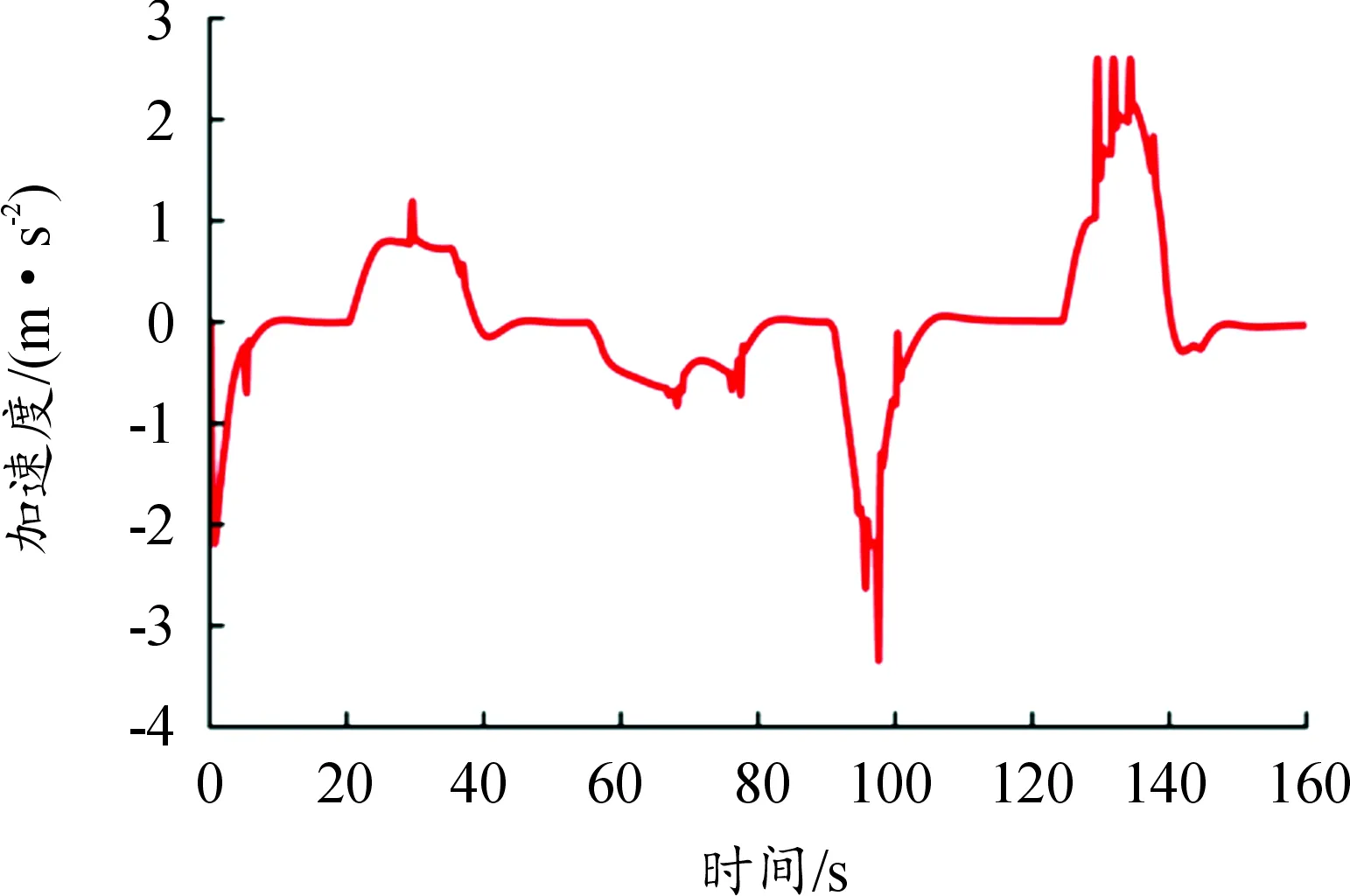
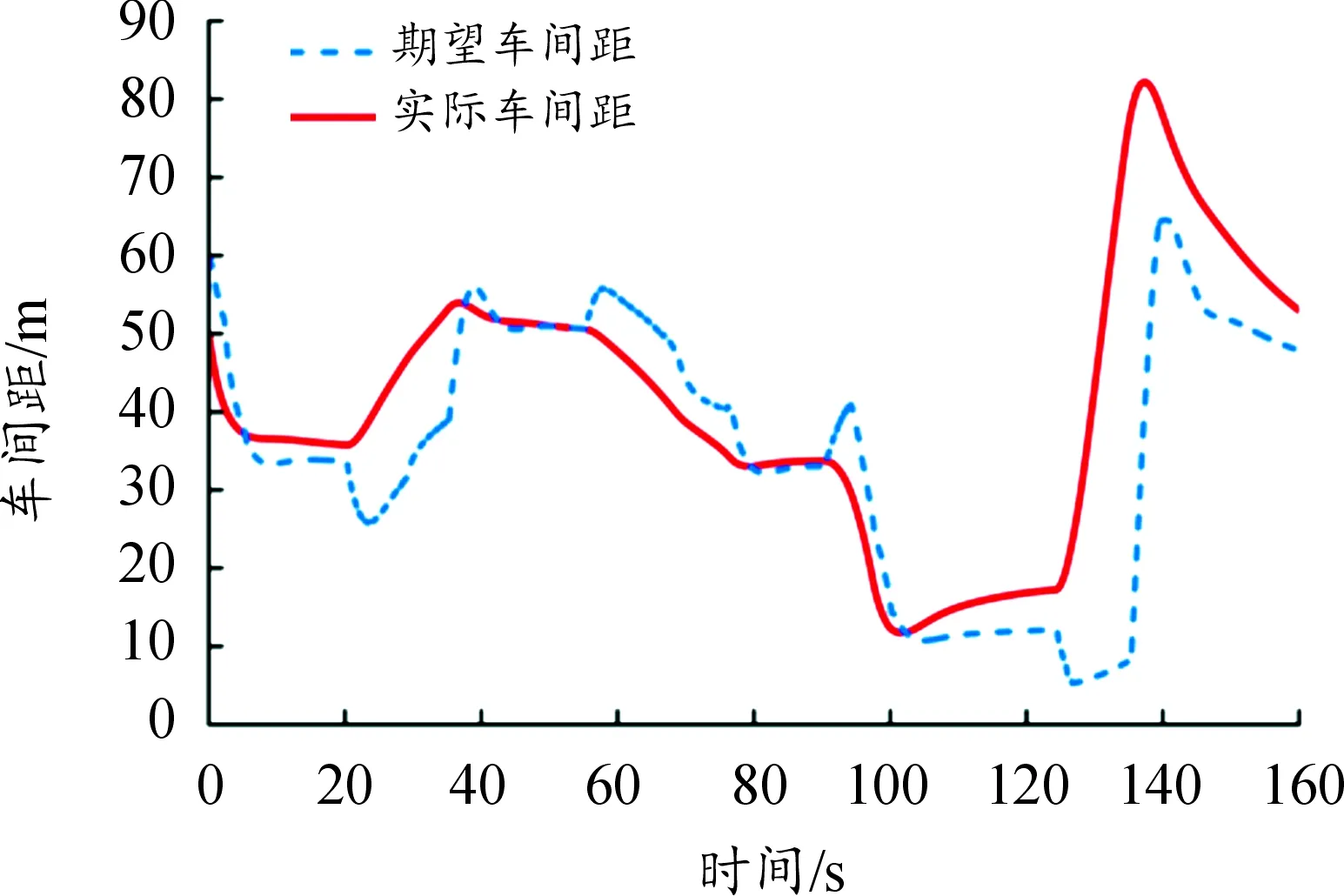
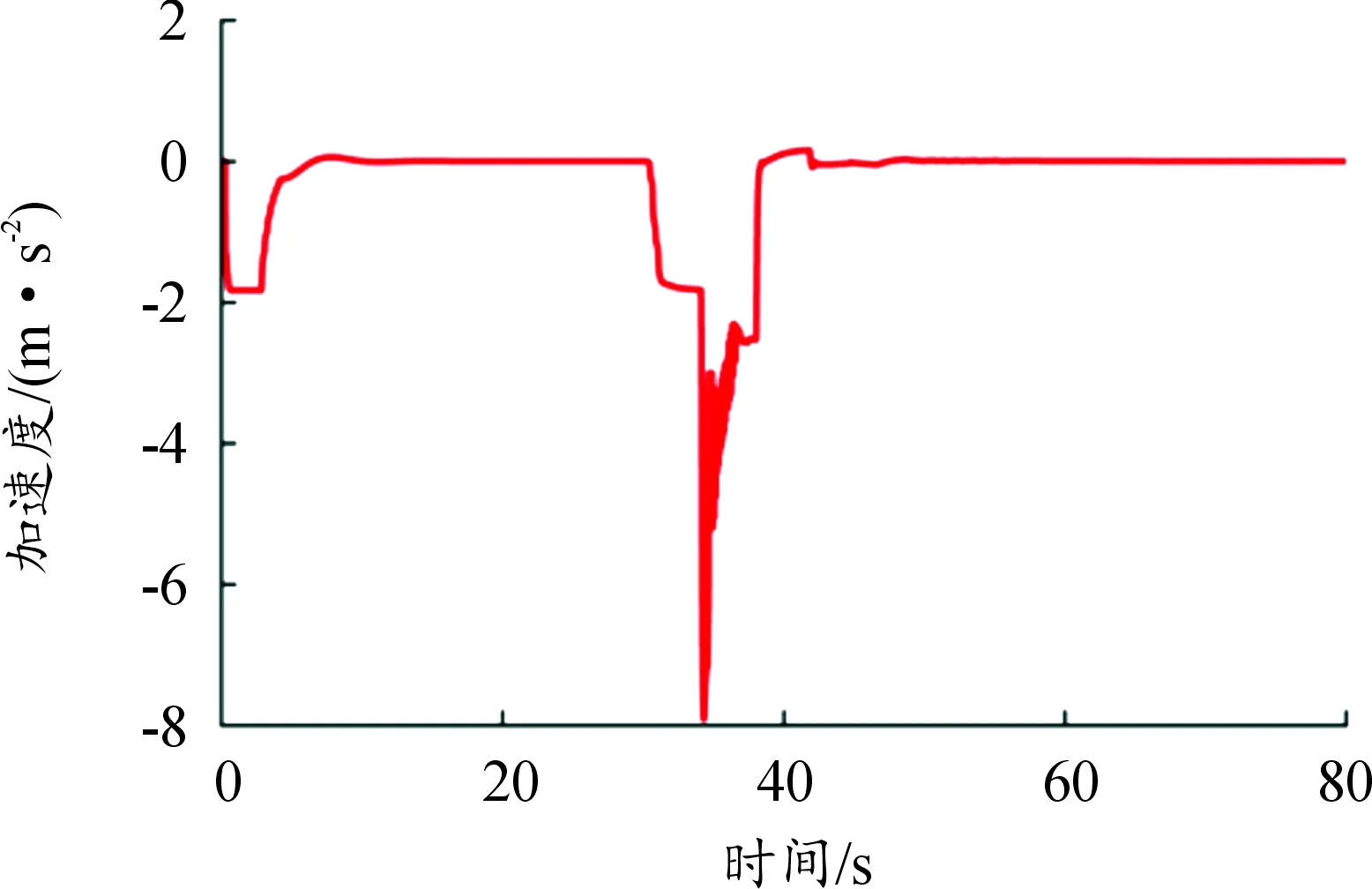
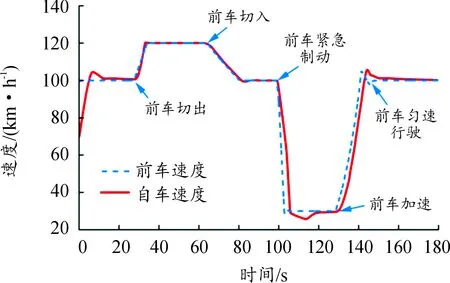
4 联合仿真验证与分析
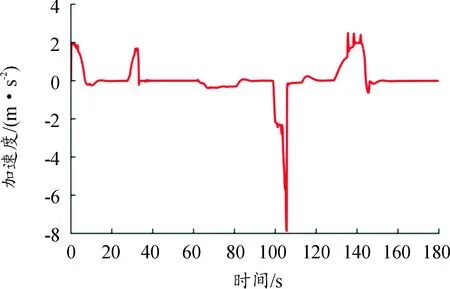
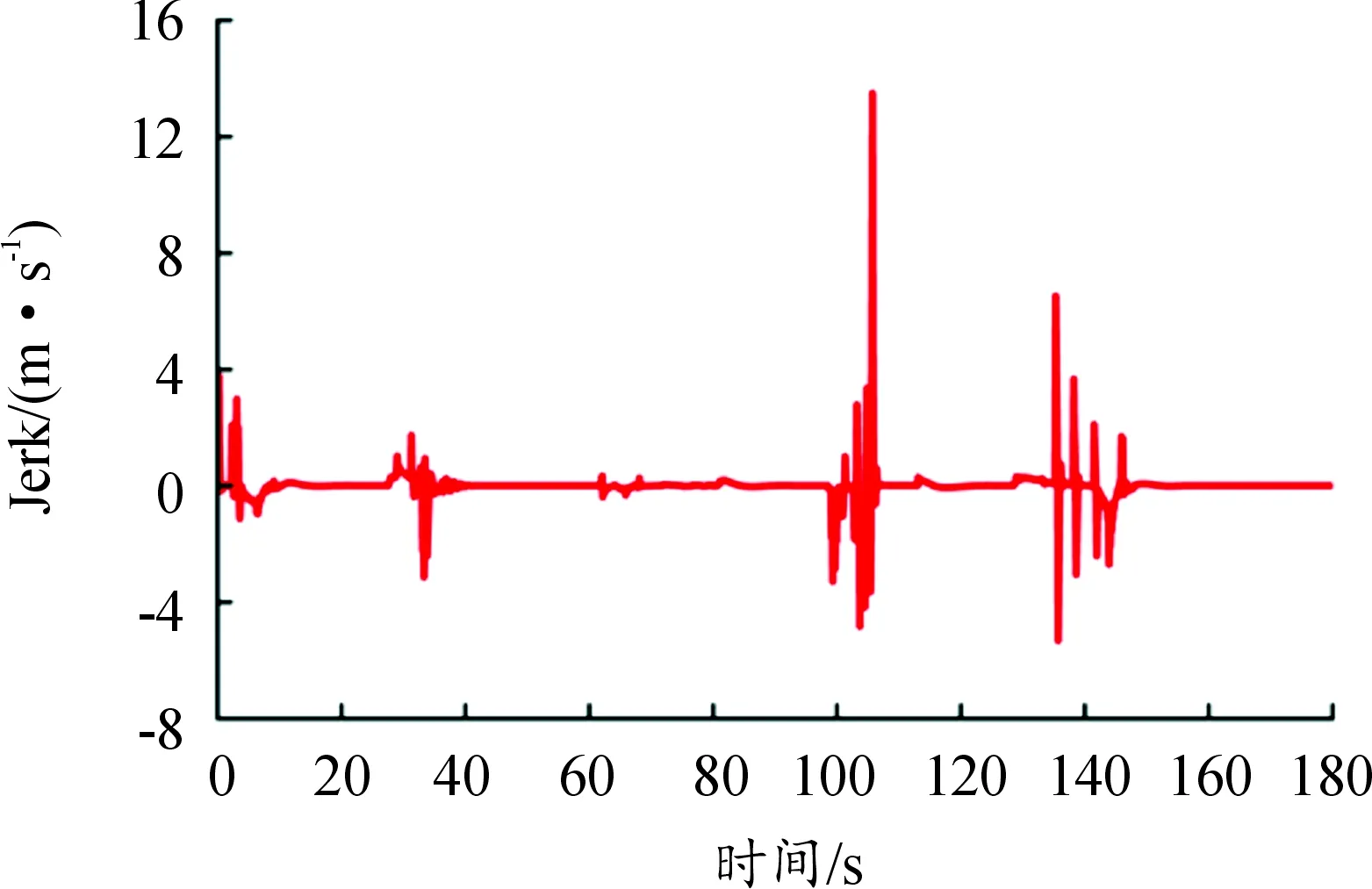
4.1 仿真工况设置与结果分析





5 结论
