灾后ATIS对城市道路交通网络韧性的影响
2023-04-11庞远兵石超峰
庞远兵,张 玺,石超峰
(1.重庆交通大学 交通运输学院, 重庆 400074;2.重庆交通大学 经济与管理学院, 重庆 400074)
道路交通网络是城市关键基础设施系统的重要组成部分,由于其拥有广泛的空间分布和复杂的地理场景,不时会受到极端自然灾害、蓄意袭击、交通事故等诸多不确定性事件的影响。在2021年郑州7.20特大暴雨灾害中,洪涝灾害造成多个区域道路损毁、交通中断,对抢险救灾工作带来了巨大阻碍,造成了巨量经济损失。由于道路交通网络中灾害发生的时空特征具有不确定性,目前还无法做到完全的灾前预防,也不可能完全消除交通运输体系的易损性和毁伤后果[1]。因此,相比于预防或减缓灾害的后果,提升道路交通系统从扰动中快速恢复和维持预定功能的能力具有同样重要的现实意义[2]。
在此背景下,韧性(resilience)的概念逐渐被引入交通领域,以描述扰动事件下交通系统吸收干扰并从中恢复的能力[3]。杨金顺等[4]系统性地总结了前人提出的韧性概念框架,将交通网络韧性定义为道路交通系统受到外界或自身的干扰(自然灾害、交通事故等)后,维持原有状态或者在一定时间期限内恢复到可接受状态的能力。Bruneau等[5]提出了经典的“韧性三角”,以灾害期间系统性能的累计损失程度来量化系统韧性;Balal等[6]则认为正常状态下的系统性能同样是一个随时间变化的函数,进一步改进了此韧性指标。考虑到系统性能累积损失大小和韧性强度呈负相关关系,李兆隆等[7]对文献[5]提出的韧性指标作了归一化处理。Nogal等[8]则将系统韧性理解为在扰动周期内从衰竭水平到完全衰竭水平的平均距离,以更为直接的方式反映了系统吸收冲击的剩余能力。扰动发生后的路网处于动态非均衡状态,文献[8-9]分别提出了确定性和考虑用户选择随机性的动态平衡限制分配模型来模拟网络性能的演化;吕彪等[10]构建了先进出行者信息系统(advanced traveler information system,ATIS)引导下的日变配流模型,以描述扰动后交通流的动态变化特征。
目前已有的研究成果皆忽略了灾后交通信息对路网韧性的重要影响。灾害发生后若出行者不能及时获取交通信息,极有可能造成路网某些关键节点拥堵失效,进而发生拥堵传播效应[11],导致整个路网彻底崩溃。ATIS作为智能交通系统的核心组成部分,能够在灾害发生后为其使用者提供完全交通信息及预测信息,有效诱导出行者选择有利的路径,保证灾后路网仍能够有效运行。而非ATIS出行者只能根据自身历史经验逐渐调整出行路径。以往的研究只考虑了全部出行者都有装备或都没有装备ATIS的情景,而忽略了不同ATIS市场占有率下的流量演化。探究灾后ATIS对路网韧性的重要影响,将有助于灾后的交通管控工作。
对此,考虑到ATIS使用者和非ATIS使用者信息获取条件不同,路径选择行为模式存在差异性,通过构建两类用户混合日变动态配流模型,以准确描述扰动事件下两类用户的路径选择行为,并在路网韧性评价中引入动态时间维度。以此为基础,通过Matlab编程进行算例仿真实验,全面分析不同ATIS市场占有率下的路网韧性。
1 道路交通网络韧性评价
1.1 符号说明
定义道路交通网络G=(N,A),其中N和A分别为路网中节点集和路段集,任一路段a∈A;W为OD对集合,W为OD对数量,Rw为OD对w∈W的可行路径集,dw为相应的固定需求;δar为0~1变量,当路段a在路径r上时δar=1,否则δar=0。引入离散时域L={0,1,…,M},其中M值足够大,任意时点t∈L表示实际中某一天。
1.2 韧性内涵
韧性强调系统应对风险事件的事前、事中、事后全过程,且韧性大小主要取决于性能的损失程度及恢复速度[12]。扰动事件下的路网性能变化如图1所示,Q(t)为t时刻的路网性能。根据扰动后的4个重要时间节点,将系统分为5种状态。4个重要时间节点为:扰动发生时刻t0、扰动结束时刻t1、修复开始时刻t2、修复结束时刻t3;5种系统状态为:系统初始稳定状态、退化状态、待修复状态、修复状态、修复后的系统稳定状态。图中t0~t1时刻的路网性能退化程度体现了系统吸收扰动影响的能力,t2~t3时刻的路网性能恢复程度和恢复速度则体现了系统从扰动中恢复的能力。阴影部分面积表示扰动造成的路网性能累积损失。
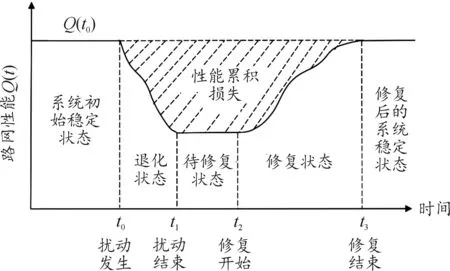
图1 扰动下的路网性能变化示意图
1.3 韧性评价指标
Nogal等[8]从路网累积性能入手,将路网韧性定义为在扰动影响期内从衰竭水平到完全衰竭水平的平均距离。该韧性评价方法具有较强的可解释性和易用性,但缺乏动态性,忽略了扰动影响期内任一时刻的路网韧性。为此,本文在该韧性评价中引入动态时间维度,改进后的路网韧性评价指标为
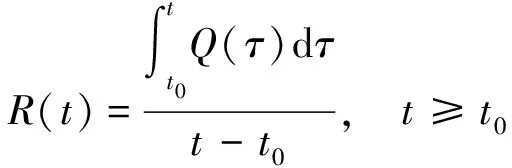
(1)

鉴于扰动事件下的路网处于非均衡状态,路网性能Q(t)采用文献[13]中的动态网络效率指标进行测度,具体描述为
(2)
式中:frw(t)和hrw(t)分别为扰动后第t天OD对w间路径r上的流量和行程时间,其中hrw(t)由路段路径关联关系求得:
(3)
式中:ta(t)表示第t天路段a的行程时间,具体可采用BPR函数描述为
ta(t)=t0,a{1+m[xa(t)/ca(t)]n}
(4)
式中:t0,a为路段a上的自由流时间;ca(t)为第t天路段a的通行能力;xa(t)表示第t天路段a的流量;m、n为给定参数。
2 两类用户混合日变配流模型
交通扰动事件可大致分为持续数小时的常规扰动事件(如车辆碰撞等)和持续数天的重大扰动事件(如极端自然灾害等)。本文主要关注持续数天的重大扰动事件下,路网流量的逐日动态演化过程。基于构建模型需要,作出以下假设:① 交通需求固定;② 每天的客流状态仅考虑当天的高峰小时段客流需求;③ 扰动事件下的路网降级过程发生在一瞬间;④ 扰动事件发生在当天出行活动之前;⑤ 路网每天的修复工作处于当天出行活动之前,且修复部分当天就可投入使用。
2.1 模型基础关系
在ATIS赋能的路网中,ATIS为其使用者提供出行信息,非ATIS使用者只能根据历史经验调整路径。因此ATIS使用者(即ATIS用户,本文中ATIS市场占有率等价于ATIS用户占比)和非ATIS 使用者(即普通用户)分别进行逐日出行路径调整,由于两部分用户出行行为的差异性,两部分流量遵从不同的动态演化规则,任意一天t∈L两部分流量之间存在如下关系
(5)
(6)
(7)
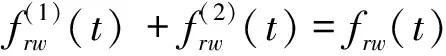
(8)
(9)
(10)

2.2 基于历史流量的ATIS信息预测方法
ATIS发布的出行信息会影响使用者的出行决策。文献[14]提出了经典的ATIS信息预测方法,此方法采用前一天的实际路径行程时间作为当天路径行程时间预测值,忽略了扰动事件下路网退化及修复过程中组件通行能力的动态变化。根据能获取完全信息的ATIS系统,路网当天的通行能力为已知,若在ATIS信息预测方法中及时采用当天实时的通行能力描述路网状态,ATIS系统将为用户提供更接近实际情况的预测。因此针对非均衡的动态路网,本文提出基于历史流量的ATIS信息预测方法

(11)
式中:Srw(t)为ATIS发布的第t天路径r的行程时间;ζ为误差项,其服从均值为0、方差为φ的独立正态分布,与时间和路径均无关,其中路段行程时间采用BPR函数描述;ca(t)为路段a在第t天的通行能力,修复过程中的路段通行能力恢复过程可描述为[15]
ca(t)=c0,aκa+c0,a(1-κa)·
{1-exp[-ηa(t-t2)]}
(12)
式中:t2≤t≤t3,c0,a为路段a的设计通行能力;κa为路段a的吸收能力参数,反映路段a的通行能力退化程度;ηa为路段a的恢复速率参数。
2.3 两类用户混合下路径流量逐日演化
扰动事件发生后路网中存在较多随机因素,出行者只能根据自己的理解行程时间选择路径,出行者的理解行程时间可描述为[14-16]
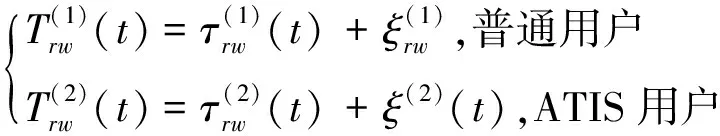
(13)

ATIS用户根据出行经验累积,他们对路网的认知差异将不断减小,方差σ(t)可表示为[14]

(14)
出行者会根据自身历史出行经验或ATIS信息对第2天的理解行程时间期望进行修正,即认知更新的过程,这种学习过程可描述为[14,16]
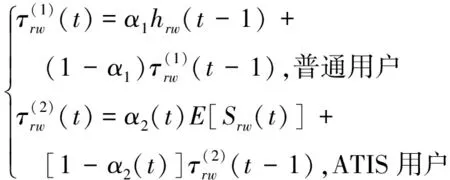
(15)
式中:α1、α2(t)∈[0,1]分别为普通用户和ATIS用户的认知更新权重系数,α2(t)与时间刻度相关,通常α2(t)≥α1,表示与普通用户相比,ATIS用户能获取更多的决策信息;E[Srw(t)]为第t天ATIS发布时间的期望值。
随着ATIS用户对于路网越来越熟悉,对ATIS信息的依赖程度将逐渐减小,α2(t)可表示为[14]
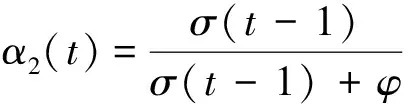
(16)
根据离散选择理论,理解误差服从Gumbel分布时,路径选择概率为Logit概率函数,则出行者在第t天对路径r的选择概率可描述为[14,16]

(17)
式中:θ1、θ2(t)分别为普通用户和ATIS用户的离差系数,表示出行者对路径行程时间的理解随机偏差程度,离差系数越大意味着随机偏差越小;通常θ2(t)>θ1,表示ATIS用户比普通用户有更小的理解误差;θ2(t)可表述为[14]
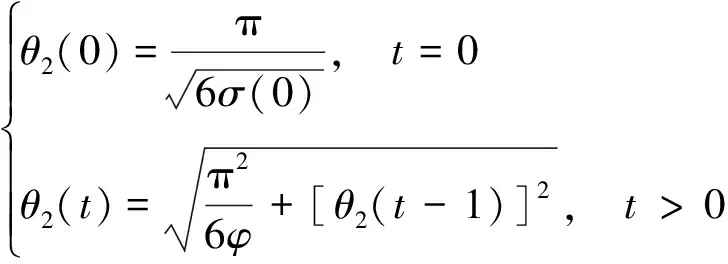
(18)
由于出行行为惯性,出行者并不会完全根据随机效用最大化原则改变当前出行路径,部分出行者仍然会选择固定的出行路径,因此扰动发生后的实际路径流量演化过程描述为[16]

(19)
式中:β1、β2∈[0,1]分别为普通用户和ATIS用户的惯性系数,是根据弱大数定理所确定的群体中重新考虑出行路径的出行者比例。
2.4 求解算法
据文献[16]可知,本文构建的两类用户混合日变动态配流模型一定存在一个不动点,意味着从任意初始状态出发,路径流量都将收敛于唯一的平稳概率分布。具体的配流方法如下:



步骤4算法终止检查。若t=M,算法终止,否则返回步骤2。
3 算例分析
在如图2所示的算例网络中,利用Matlab编程进行算例仿真实验。网络中共13个节点,19条路段,节点内的数字为节点编号,路段上的数字为路段编号。

图2 算例网络结构示意图
3.1 参数设置
网络中存在2个OD需求,分别为d12=900 veh/min、d43=600 veh/min,OD对间由节点连接表示的有效路径如表1所示;路段设计通行能力均为c0,a=300 veh/min,路段自由流行程时间均为t0,a=25 min。假设扰动事件发生前路网处于SUE状态。

表1 OD对间有效路径
算例中,扰动事件发生在第1 d,即t0=1;修复工作从第4 d开始,即t2=4;相关参数设置如下:m=0.15,n=4,α1=0.4,θ1=0.2,β1=0.2;σ(0)=102,β2=0.2,φ=52;M=50; 路段对扰动的吸收能力参数κ5=κ7=κ8=κ17=0.3,其余路段κa=0.7;所有受损路段修复速率参数均为ηa=0.3;用户比例参数γ=0.5。
3.2 路径流量演化
图3描述了扰动事件发生后部分路径流量的演变过程。可以发现在扰动初期,路径流量较大的路径1和路径14产生剧烈波动,这是由于扰动造成路网状态发生剧烈变化,出行者对于路网状态的理解出现巨大误差,导致频繁调整出行路径;而流量较小的路径13上并无太大波动,这说明流量较小的路径对于扰动的敏感性较低。随着出行者对路网状态的了解逐渐加深,路径流量波动开始逐渐变小,并在第25 d左右完全趋于稳定。
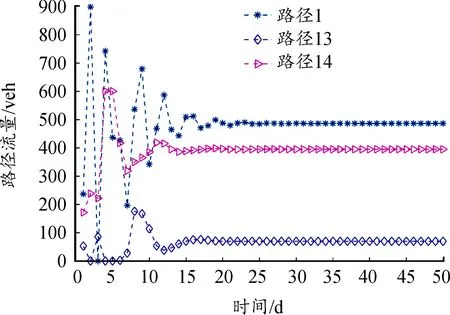
图3 扰动后的路径流量演变
图4则展示了扰动发生后路网性能的演变过程,可以看出,由于扰动事件的突发性,导致扰动初期路网性能呈断崖式下跌,到第3 d,路网性能已由初始的5.14 veh/min降低至1.57 veh/min,路网性能损失达到69.4%;第4 d修复工作开始后,路网性能开始逐步恢复,并在第25 d完全恢复至初始状态。
3.3 2种ATIS信息预测方法对比分析
图5描述了2种不同的ATIS信息预测方法下,路网韧性的动态演变。不管哪种ATIS信息预测方法下,扰动发生初期的路网韧性都呈断崖式下跌,此时路网处于极度脆弱状态,对二次灾害的抵抗能力和吸收能力都大幅降低;从第4 d修复工作开始后,路网韧性逐步恢复。但据图4描述,路网性能在第25 d就已恢复至初始值,图5表明第25 d路网韧性还处于恢复过程中,这是因为从韧性的角度来看,扰动事件对路网造成的历史影响无法完全消除,只能随时间逐渐淡化,在这一过程中路网韧性值将逐渐趋于初始值。

图4 扰动后的路网性能演变

图5 不同ATIS信息预测方法下的路网韧性动态演变
从图5中2种ATIS信息预测方法下的路网韧性对比来看,本文提出的基于历史流量的ATIS信息预测方法与经典的ATIS信息预测方法相比,在第3 d,后者支持下的路网韧性为1.7 veh/min,而前者为1.95 veh/min,相比于后者提高了14.7%;在整个研究时域内,前者支持下的平均路网韧性值相比于后者提升了2.48%。这是因为前者考虑到了扰动发生后路网退化及修复过程中路段通行能力的动态变化,根据实时的路网信息及时为出行者提供了更为精准地预测,提升了出行者对于出行当天路网状态的了解。
3.4 用户比例参数γ的敏感性分析
图6为用户比例参数γ的敏感性分析,分别选取了扰动影响期内第5、10、15、20、25 d作为研究时间节点。可以发现,在这5个时间节点下,对用户比例参数γ的敏感性分析结果呈现相同的变化趋势,即随着γ的增大,路网韧性值逐步增加,当γ等于0.7时,路网韧性达到峰值,并在之后开始缓慢下降。以第5 d为例,γ=0时,路网韧性值为1.97 veh/min;γ=0.7时,路网韧性值为2.55 veh/min,同比提升29.44%。图7进一步描述了用户比例参数γ对路网韧性的影响,可以看出,在整个研究时域内,最佳用户比例参数γ均在0.7左右。这意味着扰动事件发生后,针对路网韧性最优这一目标,最佳的ATIS市场占有率约为30%。这是由于在全部出行者都不装备ATIS时,出行者只能获取不完全信息,极易造成灾后某些关键路段或节点拥堵失效;而在全部出行者都装备ATIS时,所有出行者都能获取完全信息,他们以利己原则选择出行路径,导致在灾后剩余通行能力较大的路段或节点造成新的拥堵甚至失效。因此,在某一固定情境下,ATIS用户和普通用户之间一定存在一个“平衡点”,即一个最佳的ATIS市场占有率,使灾后路网韧性达到最优。

图6 用户比例参数γ敏感性分析

图7 不同参数γ下的路网韧性动态演变
3.5 ATIS信息误差方差φ的敏感性分析
图8描述了第5 d,在不同ATIS市场占有率下,对ATIS信息误差方差φ的敏感性分析。可以看出,当ATIS市场占有率为50%、75%、100%时,随着φ逐渐提升,路网韧性值相应增大,意味着ATIS信息误差越大反而有利于路网韧性值提升。这是因为ATIS信息误差越小时,ATIS用户对于路网状态的了解程度加深,他们偏向于选择利己的最小阻抗路径,当占比较大的ATIS用户都根据利己原则选择出行路径时,势必会造成路网性能损失;同时,ATIS信息误差越小时,权重系数α2(t)会相应增大,即ATIS用户对ATIS信息的依赖程度加深,这导致占比较大的ATIS用户频繁更换出行路径,造成扰动后的路径流量波动变大,持续时间变长。但当ATIS市场占有率为25%时,随着φ逐渐提升,路网韧性值却逐渐减小。这是因为ATIS市场占有率较小时,大部分出行者只能获取不完全信息,出行群体中无序的、随机的路径选择模式处于主导,需要较长时间路径流量才能演化至稳定状态,此时提升ATIS信息的准确性可在一定程度缩短流量波动时间。
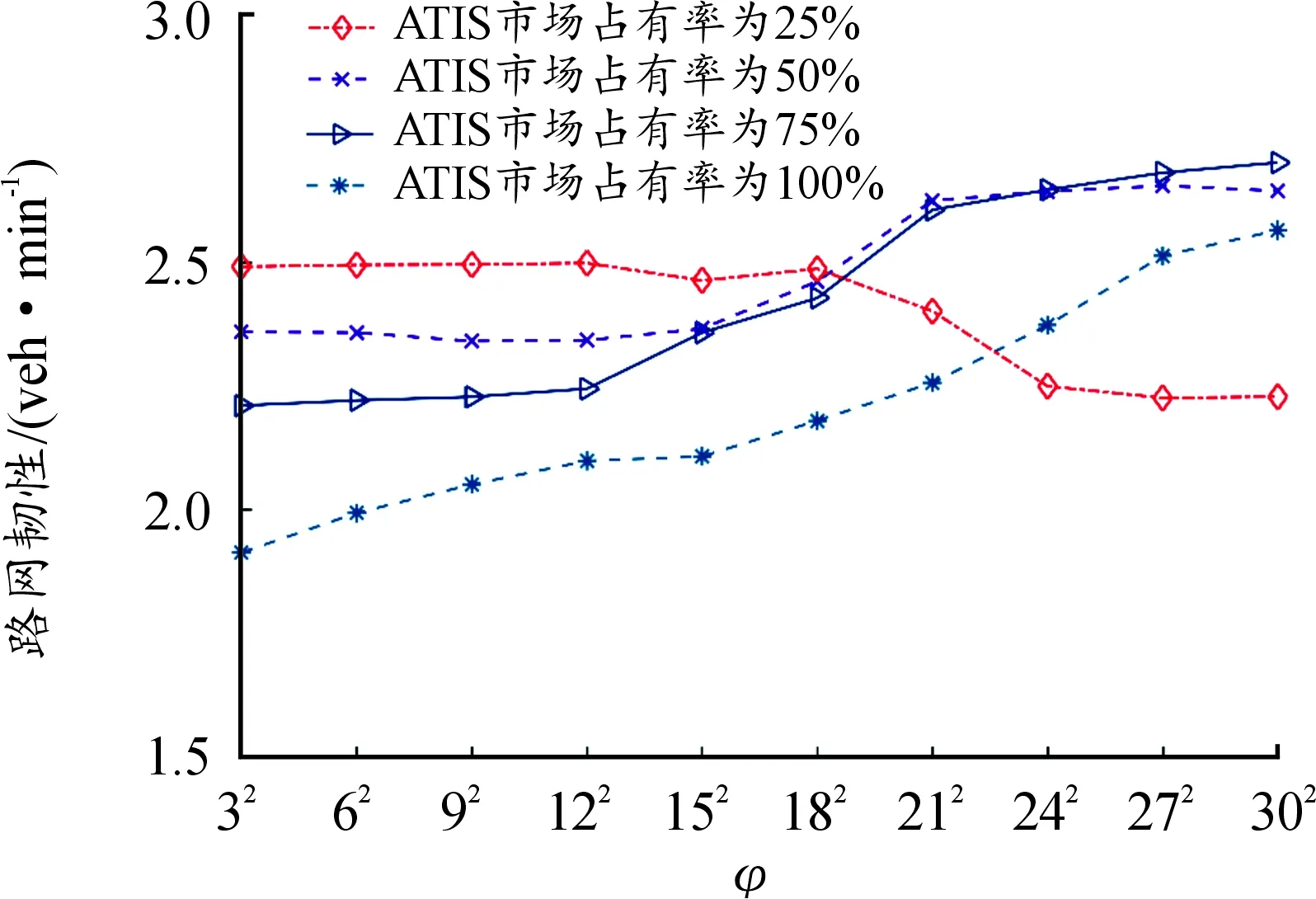
图8 参数φ的敏感性分析(t=5)
4 结论
以重大灾害下的道路交通网络为研究对象,在路网韧性评价中引入动态时间维度,在ATIS环境下,ATIS用户和普通用户由于交通信息获取条件不同,造成不同用户比例下的路网韧性呈现差异性,通过算例仿真分析得到以下结论:
1) 本文所提出的基于历史流量的ATIS信息预测方法,考虑到了扰动发生后路网通行能力的动态变化,相比于经典的ATIS信息预测方法,能够在一定程度上减少扰动后的路网性能损失。
2) ATIS市场占有率会对路网韧性值造成影响,针对韧性最优,存在一个最佳的ATIS市场占有率,使路网韧性在研究时域内始终处于峰值。表明灾后适当控制ATIS的使用比例,可有利于路网韧性的快速恢复。
3) 当ATIS市场占有率较大时,ATIS信息误差增大,路网韧性值相应提升;但当ATIS市场占有率较小时,ATIS信息误差增大会导致路网韧性值降低。表明灾后应根据不同的出行者比例,采取合理的ATIS信息发布策略。
