一类单自由度分段光滑悬索桥模型的动力学研究

侯林森,李高磊,吴 鑫,乐 源

(西南交通大学 力学与航空航天学院 应用力学与结构安全四川省重点实验室, 成都 610031)

悬索桥是一类以承受拉力的缆索作为主要承重结构的桥梁,是特大跨径桥梁的主要形式之一。对于大跨度悬索桥而言,随着桥跨的不断增加,桥的结构刚度将会大幅下降,风致抖振的发生将会影响桥体的稳定性,进而发生分岔乃至混沌的动力学现象,如果设计不当将会导致难以预计的后果。

自19世纪初悬索桥被发明以来,关于悬索桥的设计和研究便成为了工程界的热点问题之一。1940年,美国塔科马(Tacoma)悬索桥的风致坍塌震惊了整个工程界[1],大量的学者也开始注意到这一类实际的工程系统:为了研究该类系统的动力学特性,Lazer等[2]首先建立了一类单自由度分段悬索桥模型,考虑其受到周期外激励作用下的解,Glover等[3]研究了单自由度分段的悬索桥模型在恒定载荷和较小激励下周期解的存在性和稳定性,并将判别周期解存在性和稳定性的Loud隐函数理论方法推广到不可微非线性的系统。为了更好地拟合实际工程中悬索桥的运动状态,Lazer等[4]将系统扩展到更高的维度,建立了一类两自由度光滑悬索桥模型和一类两自由度分段悬索桥模型,用数值方法计算了其受到大幅度周期激励作用的解,Doole等[5]通过数值模拟出了单自由度分段悬索桥系统的相图、分岔图,观察到系统的周期倍化现象和周期共存现象,随着简单胞映射方法[6-11]的提出与改进,通过全局动力学方法分析系统的吸引子和吸引域的稳定性以及演化规律开始广泛应用于各种动力学模型,Freitas等[12]继续考虑了单自由度分段光滑的悬索桥模型,结合简单胞映射方法得到了以周期解为主的多稳态现象以及吸引域边界的结构分形,并观察到了包括周期吸引子和混沌吸引子共存,边界激变[13-20]在内的动力学现象。

继续研究单自由度分段光滑悬索桥模型,借助简单胞映射方法,研究系统在不同的参数下的多稳态动力学,并发现了周期吸引子共存、周期吸引子和混沌吸引子共存、混沌吸引子共存的丰富多稳态现象。通过打靶法计算系统的不稳定周期轨道,研究了系统的激变动力学,不同于以往的研究结果,在改变激振幅值参数B时发现,从一个鞍结点延拓出来的不稳定周期轨道随着参数的减小与共存的稳定周期1轨道重新交汇,形成了一个新的鞍结点,该研究结果表明系统在一个不稳定的运动状态下随着参数的变化可能分别对应着两个稳定的运动状态,为分析悬索桥的稳定性提供了一个新的思路,对工程实践中悬索桥的安全性分析提供有效的理论参考和一定的实践依据。

1 悬索桥力学模型

考虑了文献[3]研究的单自由度分段光滑悬索桥模型,得到运动微分方程:

y″+2cy′+k′y=W+Bsin(ωt)

(1)

其中:

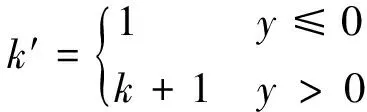
(2)

y表示垂直方向的位移,向下为正,c表示阻尼系数,k′表示悬索分段刚度系数,k表示悬索的刚度,W表示预加载力,ω表示垂直方向入射的风载荷频率。

2 简单胞映射方法的基本原理

假设微分方程为:

(3)

式中:x为实值向量,F为实值向量函数,当系统具有周期性时,F为关于t的周期函数,对式(3)在一个周期内进行积分,将系统在一个周期结束时的运动状态与下一个周期结束时的运动状态相联系,式(3)可改写为:

x(n+1)=G(x(n))

(4)

式(4)说明状态空间中的点x(n)在经过一个周期后由G映射为点x(n+1),这种点对点的映射动力系统被称为点映射或者Poincaré映射。

简单胞映射方法是通过将连续系统离散为具有离散状态空间的系统,再通过特征矢量对每个单元(胞)的表征近似地描述连续系统的状态变量。假设连续系统的N维欧式状态空间为RN,将状态变量的坐标轴xi(i=1,2,…,N)分成无数个整数区间,间距为hi,其中每个区间Zi表示一个胞单元,每一个胞单元Zi中包含的xi范围为:

(Zi-1/2)hi≤xi<(Zi+1/2)hi

(5)

那么系统的状态矢量就可以用N维胞矢量Z表征。将每个胞视为实体,那么z(n)到z(n+1)的胞映射便与x(n)到x(n+1)的点映射方程(4)关联起来,得到:

z(n+1)=c(z(n)),Zi(n+1)=Ci(z(n))

(6)

c表示一个映射函数,式(6)这样的映射关系称为胞映射,简单胞映射方法可以通过数值方法计算求解非线性复杂系统的吸引子和吸引域等全局动力学特性。

3 全局动力学分析

3.1 阻尼系数c对全局动力学的影响

取系统参数为W=1,k=50,B=3.0,ω=1.2,考虑随着阻尼系数c增加时系统的全局动力学特性。图1、图2分别为c∈(0.02,0.03)和c∈(0.132,0.152)时的分岔图。图1中的青绿色竖线位置表示c=0.021 0,此时存在着蓝色轨线表示的周期4吸引子,黑色轨线表示的周期4吸引子以及洋红色轨线表示的周期12吸引子共存,当阻尼系数c增大到0.023 0(图1中橙色竖线位置时),黑色轨线表示的周期4吸引子退化为周期2的吸引子,此时系统表现为周期2、周期4和周期12吸引子共存的运动状态,随着阻尼系数c的进一步增大,当c=0.024 2,如图1中紫色竖线位置所示,洋红色轨线表示的周期12吸引子也发生了退化,变为周期6的吸引子,这时系统处于周期2、周期4、周期6吸引子共存的运动状态,当c继续增大到0.025 5,图1中红色竖线位置,此时蓝色轨线表示的周期轨道在进入混沌后消失,此时系统仅表现为黑色轨线表示的周期2吸引子和洋红色轨线表示的周期6吸引子共存的运动状态。从图2中可以观察到,在c=0.136 5处,存在着混沌吸引子与周期吸引子共存,在c=0.139 5处存在着周期2和周期4吸引子共存,如图2中蓝色竖线和黄色竖线位置所示。

借助胞映射方法,可以进一步通过系统的吸引子和吸引域的稳定性和演化规律来研究系统的多稳态动力学,图3分别对应图1和图2中不同竖线位置的阻尼系数c下吸引子和吸引域。

图1 c∈(0.02,0.03)时不同初值下的分岔图

图3 不同阻尼系数c下系统共存的吸引子及其吸引域

图3(a)为c=0.021 0时系统的吸引子和吸引域,系统存在着蓝绿色圆点表示的周期4吸引子,红色圆点表示的周期4吸引子以及黑色圆点表示的周期12吸引子共存,它们的吸引域分别用深蓝色、靛蓝色以及黄色的区域表示,可以观察到3个吸引子的吸引域相互纠缠嵌套在一起且具有分形结构,说明在此状态下系统对初值比较敏感,任何一个微小的扰动都可能使系统从一个运动状态跳跃到另一个运动状态,这样的吸引域称为“Wada域”[21]。图3(b)为c=0.023 0时系统的吸引域,其中青绿色区域表示周期2运动状态的吸引域,吸引子用洋红色圆点表示;黄色区域为周期4运动状态的吸引域,吸引子用深蓝色圆点表示;蓝色区域为周期12运动状态的吸引域,吸引子用红色圆点表示,系统在此参数状态下表现为周期2、周期4、周期12吸引子共存。图3(c)为c=0.024 2时系统的吸引子和吸引域,系统表现为周期2、周期4、周期6吸引子共存,吸引子分别用红色、洋红色和黑色来表示,对应的吸引域颜色分别为黄色、深蓝色和青绿色。图3(d)为c=0.025 5时的吸引子和吸引域,此时对应分岔图中的蓝色轨线突然消失,只剩下2种运动状态的吸引子共存,即绿色圆点表示的周期2吸引子和红色圆点表示的周期6吸引子共存,它们的吸引域分别用黄色和紫色表示。当c增加到0.136 5时,如图3(e),系统表现为周期4吸引子与混沌吸引子共存,青绿色的圆点表示周期4的吸引子,从深蓝色区域出发的轨道可以吸引到周期4吸引子上。红色的离散点组成的区域为混沌吸引子,从黄色区域出发的轨道可以吸引到混沌吸引子上,与前4组参数下的吸引子与吸引域相比,在此参数下周期运动的稳定性相对较高,因为吸引域嵌套程度比较低,吸引域的边界不再具有“Wada域”的特性,随着阻尼系数c进一步增大到0.139 5时,如图3(f),原本的周期4的运动状态退化为周期2的运动状态,而原本的混沌运动状态退化为周期4的运动状态,其中周期2吸引子用青绿色圆点表示,深蓝色区域为其吸引域,周期4的吸引子用红色圆点表示,黄色区域为其吸引域。

3.2 激振频率ω对全局动力学的影响

固定其他参数分别为W=1,k=50,B=3.0,c=0.075,通过数值模拟得到系统在不同初值下,随激振频率ω变化的多个吸引子共存的分岔图,如图4和图5所示。图4为ω∈(0.657,0.666)时的不同初值分岔图,可以观察到在蓝色竖线位置,ω=0.658时存在着周期4吸引子和周期6吸引子共存,当ω增大到0.660橙色竖线位置时,周期4吸引子退化为周期2吸引子,周期6吸引子退化为周期3吸引子,此时系统为周期2的吸引子和周期3的吸引子共存。图5为不同初值下ω∈(0.714,0.724 5)时的分岔图,蓝色竖线ω=0.715处,存在着周期3的吸引子和周期4的吸引子共存。在橙色竖线ω=0.724处,存在着混沌吸引子与混沌吸引子共存,且黑色的混沌吸引子分为3片独立的混沌区域,洋红色吸引子则为一整片的混沌区域。

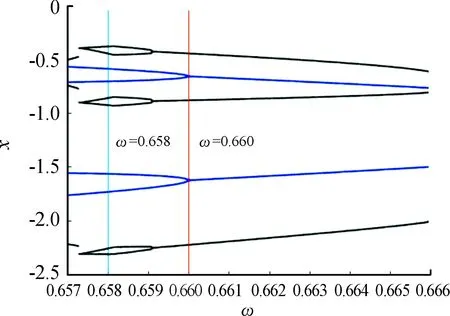
图4 ω∈(0.657,0.666)时不同初值下的分岔图

图5 ω∈(0.714,0.724 5)时不同初值下的分岔图

为了进一步分析系统的多稳态现象,通过胞映射方法得到系统随激振频率ω变化时的吸引子及其吸引域,如图6所示。图6(a)为ω=0.658时的吸引域,此时系统存在着周期4和周期6共存的吸引子,其中绿色圆点表示周期4的吸引子,其吸引域用深蓝色区域表示;周期6的吸引子用洋红色圆点表示,其吸引域用黄色区域表示。从图中可以看出,深蓝色区域的面积比黄色区域的面积大,说明深蓝色区域周期4吸引子的局部稳定性比黄色区域周期6吸引子的稳定性要高。当ω增加到0.660时,如图6(b)所示,系统从周期4吸引子和周期6吸引子共存退化成周期2和周期3的吸引子共存,吸引子分别用红色圆点、绿色圆点表示,对应吸引子的吸引域分别用深蓝色区域、黄色区域表示。此时的吸引域与ω=0.658具有相同的分形结构。当ω进一步增大到0.715,如图6(c)所示,此时系统为周期3吸引子和周期4吸引子共存,红色圆点表示周期3吸引子,从深蓝色区域出发的轨道可以吸引到周期3的吸引子上,黑色圆点表示周期4的吸引子,从黄色区域出发的轨道可以吸引到周期4的吸引子上。周期3和周期4吸引域的边界缠绕嵌套在一起,系统的稳定性进一步降低。图6(d)为ω=0.724时的吸引子和吸引域,这时系统存在着混沌吸引子共存,其中红色离散的圆点组成的三片独立的混沌区域与绿色离散的圆点组成的混沌吸引子共存,其中红色混沌吸引子的吸引域用黄色区域表示,绿色混沌吸引子的吸引域用蓝色区域表示。

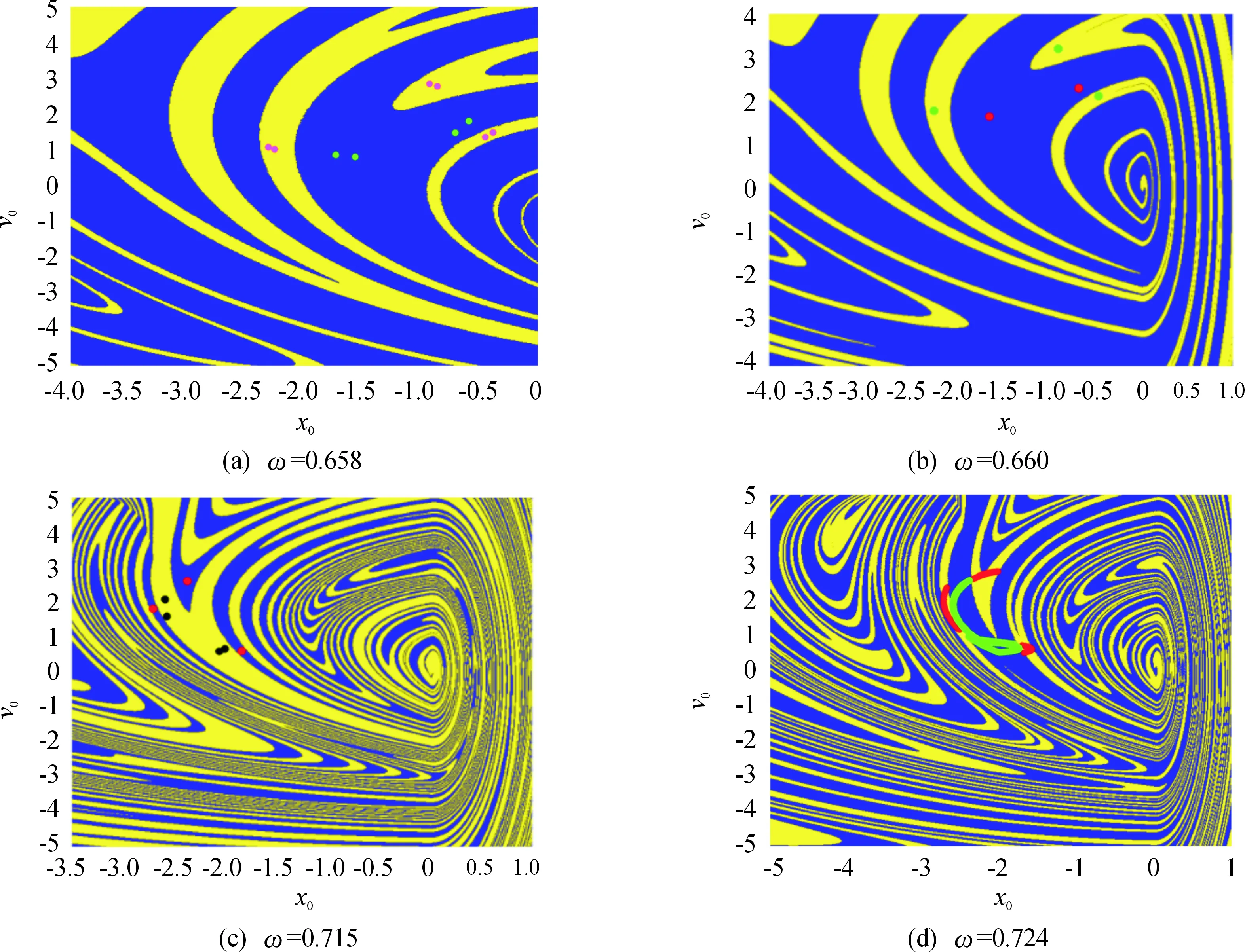
图6 不同激振频率ω下系统共存的吸引子及其吸引域

4 激变动力学

4.1 激振频率ω为参数的激变动力学

激振频率ω是系统的主要参数之一,研究系统在激振频率下的激变动力学,为工程实际中悬索桥的安全检测和维护提供了有效的理论依据。图7为ω∈(0,1.5)时的分岔图,此时,W=1,k=50,B=3.0,c=0.05。可以观察到,当0<ω<1.35时,系统存在周期运动和混沌运动交替出现的动力学现象,由于该系统是一个分段系统,在ω=0.707 5以及ω=0.978处分岔图出现了跳跃的现象。1.35<ω<1.5时,系统进入稳定的周期1运动状态。

图7 ω∈(0,1.5)时系统的分岔图

为了更深入地研究系统的激变机制,取ω∈(0.54,0.57)时的子区间分岔图,如图8所示,绿色虚线表示不稳定周期轨道,洋红色区域表示混沌吸引子。可以观察到,当ω∈(0.54,0.57)时,系统存在着同时出现周期运动和混沌运动的情况,这说明存在周期吸引子和混沌吸引子共存的多稳态现象。考虑随着ω减小时系统的动力学现象,首先在ω=0.565处,系统发生鞍结分岔(SN),当ω减小到0.563 1时,鞍结分岔产生的一支不稳定的周期轨道与混沌吸引子发生接触,混沌吸引子突然消失,系统发生了边界激变(BC),此时只存在周期1的运动状态,当ω减小到 0.551 4时,系统发生周期倍化(PD),系统由原先的周期1运动倍化为周期2运动,随着ω的进一步减小,当ω=0.546 4时系统再一次发生周期倍化,由周期2倍化为周期4,最终在ω=0.544 9处,通过周期倍化进入了混沌运动状态。当ω减小到 0.542 8时,鞍结分岔产生的不稳定周期轨道与混沌吸引子接触,发生了内部激变(IC),导致了混沌吸引子大小突然性增大。

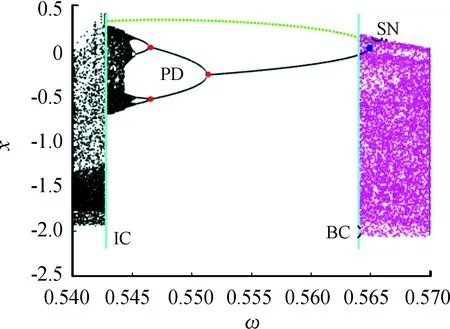
图8 ω∈(0.540,0.570)时不同初值下的系统分岔图

借助胞映射方法,通过数值模拟得到系统的吸引域,可以更细致地研究系统随激振频率ω变化时的全局特性。图9为系统在不同的激振频率下的吸引子和吸引域。

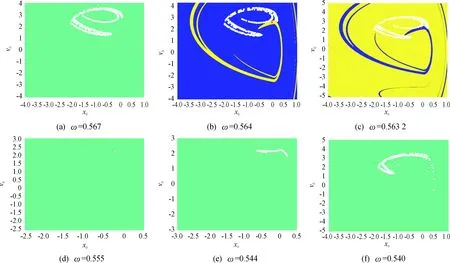
图9 系统在不同激振频率ω下的吸引子和吸引域

图9(a)为ω=0.567时系统的吸引子和吸引域,此时不存在吸引子共存的现象,系统为混沌运动,白色区域为混沌吸引子,绿色区域为混沌吸引子的吸引域。如图9(b)所示,当ω=0.564时,周期1吸引子与混沌吸引子共存,红色圆点表示周期1吸引子,黄色区域表示周期1吸引子的吸引域。图中白色离散的点为混沌吸引子,整个深蓝色区域都是混沌吸引子的吸引域。如图9(c)所示,当ω减小到0.563 2时,此时系统仍处于周期1和吸引子和混沌运动状态共存,白色离散点组成的区域为混沌吸引子,整个黄色区域为它的吸引域,红色圆点为周期1的吸引子,深蓝色区域为周期1吸引子的吸引域。通过图9(b)(c)的对比,可以观察到随着ω的减小,周期1吸引子的吸引域不断向混沌吸引子靠近,且以针状结构不断的占据原混沌吸引子的吸引域,当ω继续减小到0.563 1时,鞍结分岔的不稳定周期轨道与混沌吸引子发生接触,导致系统发生边界激变,混沌吸引子及其吸引域突然消失。图9(d)为ω=0.555时的吸引子和吸引域,此时系统仅存在一个周期1的吸引子,整个青绿色区域都是它的吸引域。对应于图8的分岔图,洋红色的混沌吸引子和绿色的不稳定周期轨道发生了接触,导致洋红色的混沌吸引子区域突然消失。随着ω继续减小,系统通过周期倍化进入混沌状态,图9(e)为ω=0.544时的吸引子和吸引域,图中白色离散点组成的区域表示混沌吸引子,青绿色区域表示其吸引域。当ω减小到0.542 8时,鞍结分岔的不稳定周期轨道与混沌吸引子发生了接触,系统发生内部激变。当ω=0.540时,如图9(f)所示,此时混沌吸引子的大小相较于ω=0.544时出现了显著的增大,在图8的系统分岔图中也可以观察到在ω=0.542 8附近,混沌吸引子的大小发生了突然性增大,再次说明系统发生了内部激变。

4.2 激振幅值B为参数的激变动力学

激振幅值B也是系统的主要参数之一,考虑系统随激变幅值改变时的响应对分析风载荷作用下悬索桥的动力学现象有一定的现实意义。考虑在参数W=1,k=50,ω=0.6,c=0.075时,系统随激振幅值B变化的激变动力学。图10为激振幅值B∈(1.5,3)的分岔图。可以观察到存在着大量的周期窗口和混沌窗口交替出现的情况。为了更清楚地观察系统的激变现象,取图10的子区间B∈(1.96,2.44)观察系统的激变现象,如图11所示,图中绿色虚线表示不稳定的周期轨道,红色区域、洋红色区域表示共存的周期吸引子或混沌吸引子。考虑随着激振幅值B减小时分岔图的变化,首先当B∈(2.394 1,2.45),系统表现为混沌运动状态,当B减小到2.41时,系统发生鞍结分岔,从鞍结点分出一支稳定的周期轨道和一支不稳定的周期轨道,当不稳定周期轨道在B=2.394 1处与洋红色所表示混沌吸引子的边界发生接触时,混沌吸引子突然消失,系统发生边界激变。当激振幅值B继续减小到2.255时,出现黑色轨线表示的稳定周期1的轨道与红色区域表示的混沌吸引子共存的动力学现象。随着B值继续减小,当B=2.177时,稳定的周期轨道发生周期倍化,并在B=2.099处再次发生周期倍化,直至进入混沌状态。而红色区域表示的共存的混沌吸引子在B=2.089退化周期1吸引子。当激振幅值B进一步减小到2.031时,不稳定周期轨道与混沌吸引子内部区域的边界发生接触,系统的吸引子尺寸出现突然性增大,此时系统发生了边界激变,当B最终减小到2.015时,绿色虚线表示的不稳定周期轨道和红色轨线表示的共存周期1吸引子轨线发生交汇,产生一个鞍结点,形成了一个新的鞍结分岔。

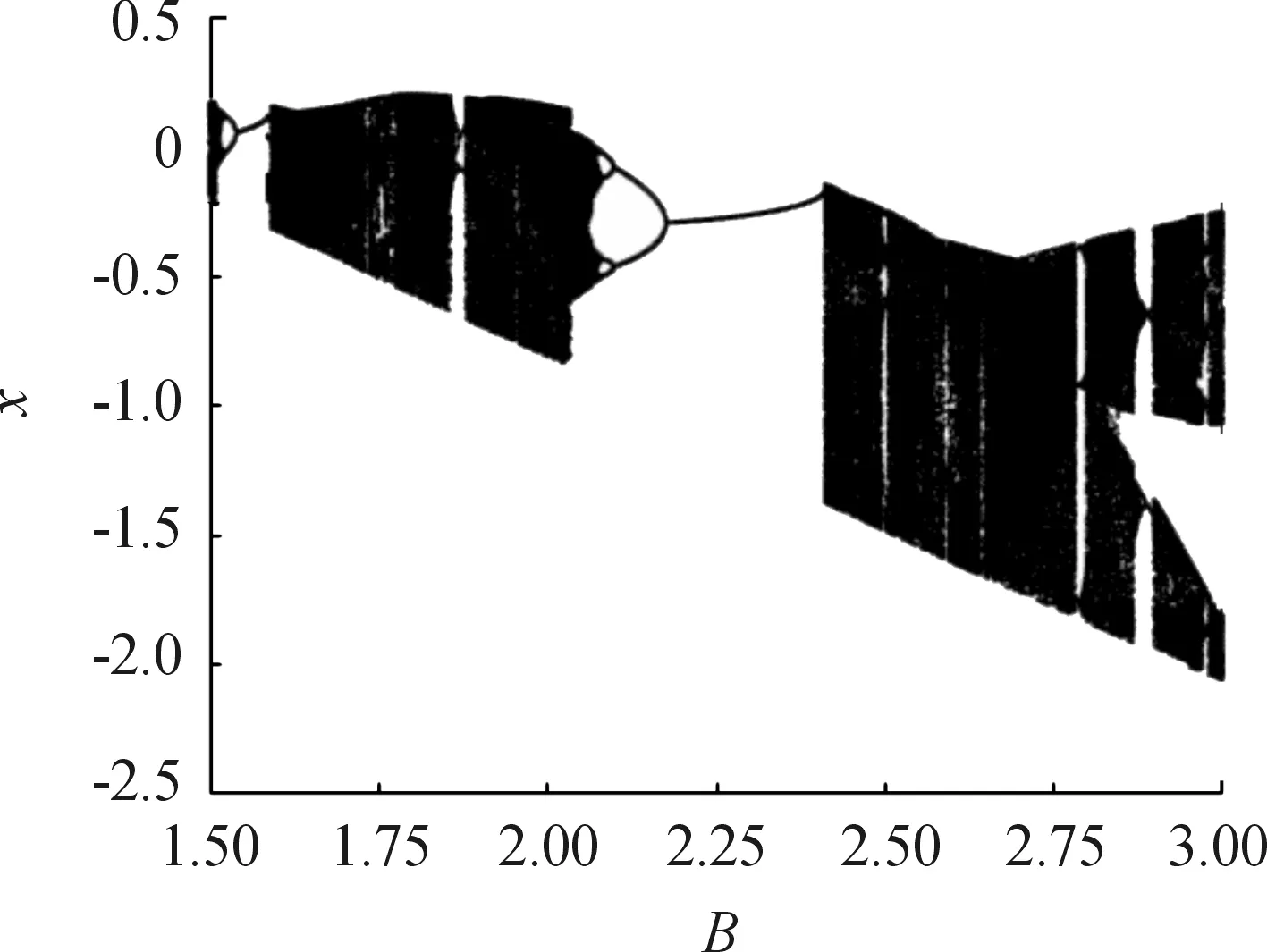
图10 B∈(1.5,3)时系统的分岔图

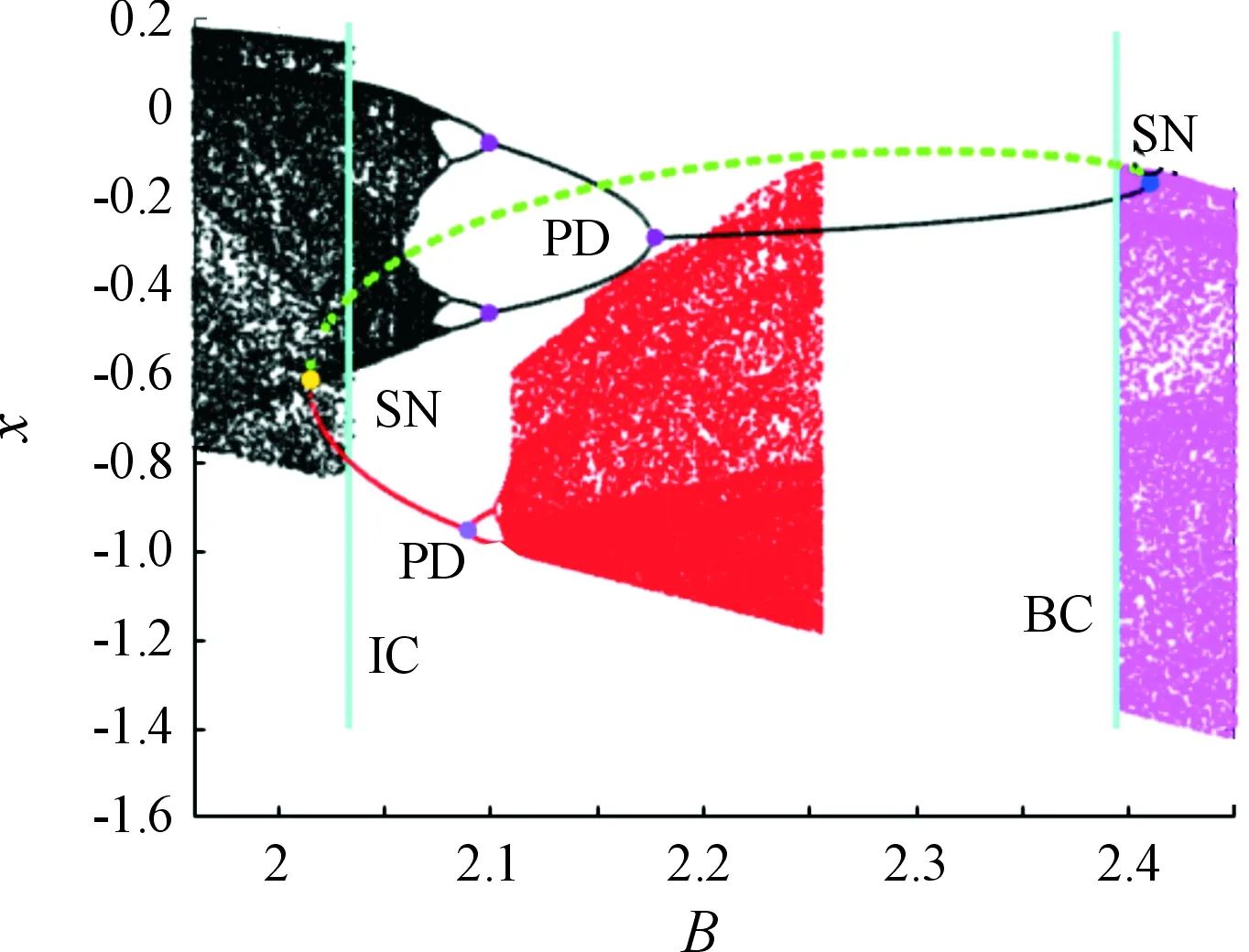
图11 B∈(1.96,2.44)时不同初值下系统的分岔图

图12为系统在不同的激振幅值下的吸引子和吸引域,图12(a)为B=2.42时的吸引子和吸引域,此时系统处于混沌状态,白色部分为其吸引子,青绿色区域为其吸引域。图12(b)(c)分别为B=2.398和B=2.396时的吸引子和吸引域,此时系统处于周期1吸引子和混沌吸引子共存的状态,红色圆点表示周期1吸引子,整个黄色区域为周期1吸引子的吸引域,白色区域组成的离散部分表示混沌吸引子,深蓝色区域为其吸引域。随着B值的减小,周期1吸引子的吸引域以针状结构不断占据混沌吸引子的吸引域。当B=2.394 1时,系统发生边界激变,不稳定的周期轨道与外部吸引子的边界发生接触。混沌吸引子突然性消失。如图12(d)所示,当B=2.393时,系统混沌吸引子完全消失,只存在白色圆点表示的周期1吸引子,青绿色区域为周期1吸引子的吸引域。图12(e)和图12(f)分别为B=2.035和B=2.030时的吸引子和吸引域,此时系统表现为周期1吸引子和混沌运动状态共存,红色圆点表示共存的周期1吸引子,黄色区域表示周期1吸引子的吸引域,白色区域表示混沌吸引子,蓝色区域为混沌吸引子的吸引域。可以通过吸引子和吸引域观察到在B=2.031处系统的混沌吸引子尺寸出现了突然性增大,此时系统发生了内部激变。

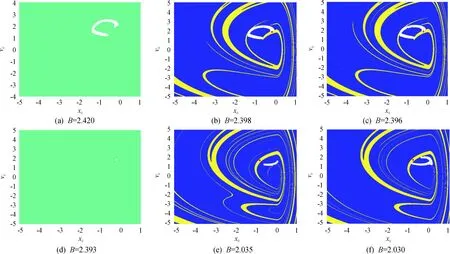
图12 系统在不同激振幅值B下的吸引子和吸引域

5 结论

考虑了一类悬索桥模型,通过数值的方法研究了系统在特定参数下的动力学特性。通过改变阻尼系数和激振频率,利用分岔图计算出不同周期吸引子共存、周期吸引子和混沌吸引子共存以及混沌吸引子和混沌吸引子共存的丰富多稳态现象,运用简单胞映射方法数值模拟得到它们的吸引子和吸引域,进一步说明了多种不同吸引子共存的现象。利用打靶法求出系统的不稳定周期轨道,通过改变激振频率和激振幅值分别得到系统的分岔图,观察到不稳定周期轨道与混沌吸引子接触时出现的2种不同的激变现象,即内部激变和边界激变。通过研究激变现象附近参数的吸引域变化,阐述了激变的原理:当混沌吸引子与在其吸引域外部边界上的不稳定周期轨道接触时,激振频率参数通过激变临界值时混沌吸引子的稳定性完全突然丧失,该类激变称为外部激变;当混沌吸引子与其吸引域内部的不稳定周期轨道接触时,激振频率参数通过激变临界值,混沌吸引子的大小发生突然性变化,该类激变称为内部激变。本文的研究结果对实际工程中悬索桥的设计以及提高悬索桥在风致颤振的下的稳定性有一定的理论参考意义。