基于高阶思维培养的数学深度教学

【摘 要】通过勾股定理三种典型教学案例的比较可发现，由低阶思维爬升至高阶思维，抓“四基”提“四能”，加强“五个重视”（重视活动、合作、思维、感悟、质疑），可以使人文精神、探究精神、科学精神等入心入脑形成自觉意识，是实现数学深度教学的基本路径。

【关键词】低阶思维；高阶思维；深度教学；初中数学

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2023）07-0042-05

【作者简介】贾保柱，江苏省昆山市娄江实验学校（江苏昆山，215300）教师，正高级教师，江苏省数学特级教师。

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）出台后，初中数学教育的发展变革大约有两个方向。第一，横向人文统整的初中数学教学。［1］ 第二，以低阶思维奠基，重视高阶思维发展的纵向深度教学。那么，这样的教学距离深度教学，距离新课标理念还有多远？

课程改革20年的理论依据主要来自人本主义、建构主义、多元智能理论、教育目标分类学等。其中布鲁姆的“教育目标分类学”将思维过程具体化为6个教学目标。其中记忆、理解、应用是低阶思维；分析、综合、评价和创造为高阶思维，主要指向创新能力、问题求解能力、决策力和批判性思维能力等。2011年版《义务教育数学课程标准》的课程理念，大多生长于这些理论。课程理念虽然不足千字，但其中“活动”出现6次、“合作探究”出现4次、“思维”出现5次、“感悟”出现3次、“创新质疑”出现3次。这些反复出现的关键词，依然是新课标中的热词，并且加持“深度学习”理论作为依据的特征比较明显，指引数学教育重视引导学生自主学习、探究学习、合作学习，发展各种关键能力。

2019年《关于深化教育教学改革全面提高义务教育质量的意见》把“五育”并举、立德树人作为国家战略层面对教育的要求。新课标将正确价值观、数学关键能力和必备品格作为数学学科核心素养的主要目标。由此可以看出情感、意志、价值观等已经成为必备品格的主要内涵，是从低阶思维到高阶思维，走向深度教学的“最后一公里”。

如果我们以低阶思维为基础，以高阶思维为杠杆，在教学活动中重视学生的活动、重视学生的合作、重视学生的体验与感悟、重视学生的质疑（在“五个重视”［2］中：活动、合作，为了探究；重视思维主要是指低阶思维、高阶思维；感悟需要经历体验；质疑能够培育创新），那么我们的数学教学不仅可以实现由低阶思维到高阶思维的系列培育，还能培养合作精神、质疑精神，触及学生的心灵深处。［3］ 这样的数学教学在发展学生的理性思维的同时，还有助于培养学生的情感态度和价值观，提升其思想水平和精神境界，从而实现深度教学。下面，笔者以“勾股定理”三种不同的教学为例，探索从高阶思维教学逐步走向深度教学的基本路径。

一、问题提出：基于勾股定理的三种典型教学

（一）教学案例一

1.三角形三边关系复习与运用

学校数学实验室正在装修，需要一个三角形框架作为装饰，三角形的两条边要求为15cm和20cm，你知道第三边的范围吗？依据是什么？

2.教师提问

直角三角形三边关系会有更特殊的结论吗？

3.引导学生猜想

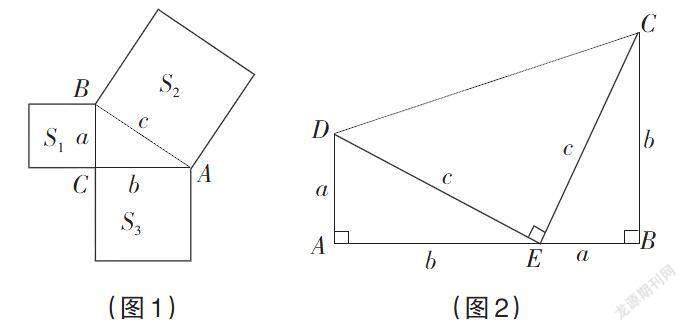
一般直角三角形三边外作正方形，有类似关系S1 + S3 = S2。（如图1）

由S1 + S3 = S2，得a2 + b2 = c2（我们称之为“勾股定理”）。

4.总统证法介绍（如图2）

5.勾股定理公式变式推导

直角三角形两直角边分别为a、b，斜边为c，有c = [a2+b2]，b = [c2-a2]，a = [c2-b2]。

6.勾股定理的運用

（1）在Rt△ABC中，∠C=90°，已知a=3，b=4，求c。变式运用：已知a∶b=3∶4，c=10，求a、b。

（2）分类求边：在Rt△ABC中，已知a=3，b=4，求c。

（3）面积法求高：直角三角形两直边6、8，求斜边上高。

（4）一般三角形求高：三角形三边6、7、8，求6上的高。

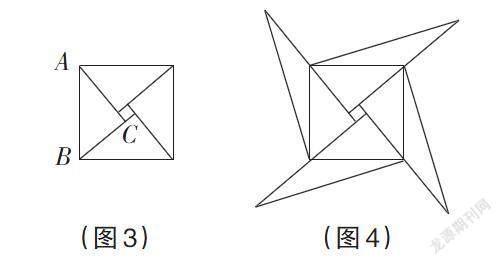
（5）“赵爽弦图”应用。

图3是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的。在Rt△ABC中，若直角边AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍。得到如图4所示的“数学风车”。则这个风车的外围周长是多少？

（6）实际应用（方程建模）：梯子问题、荷花问题、折纸问题。

（7）面积法证明勾股定理。

（二）教学案例二

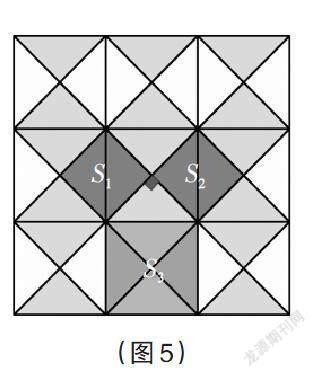
1.讲述毕达哥拉斯的故事

毕达哥拉斯应邀参加聚会，休息时随意在方格地板上画正方形（如图5），发现以等腰直角三角形三边向外作正方形面积之间的关系，猜想出直角三角形三边平方的关系。

2.再找3、4、5这样的整数边，用割补法得面积关系SA+SB=SC，推知勾股定理a?+b?=c?

3.引导学生理解勾股定理公式变式

4.勾股定理的运用

（1）计算勾股树面积。

如图6是一棵勾股树。其中所有的四边形都是正方形，所有的三角形都是直角三角形。若正方形A、B、C、D的面积分别为2、5、1、2，则最大的正方形E的面积是       。

（2）知两边求第三边。

（3）分类求边。在 Rt△ABC中，已知 a=3、b=4，求c。

（4）面积求高。直角三角形两直边长度为6和8，求斜边上高。

（5）数学史介绍：①用“赵爽弦图”证明勾股定理；②弦图运用练习。

（三）教学案例三

教师在课前向学生展示美丽的勾股树。

1.介绍数学家毕达哥拉斯的故事。（前文已提及，在此不再呈现）

2.教师带领学生，在格点图中探索直边长度为3、4的外作正方形的面积关系，类比猜想直角三角形三边关系也成立

如图7和图8，教师示范“补”的验证、学生独立尝试 “割”的验证。

3.引导学生尝试探求直边为其他整数时，外作三个正方形的面积关系

仿照上面探索：在方格纸上，画一个顶点都在格点上的直角三角形，并分别以这个直角三角形的各边为一边向三角形外作正方形。

学生任意选择一组直边整数数值，在格点图中继续类似探索，自主使用“补”或“割”的方法。

学生展示探索成果的同时，教师引导学生思考由斜边向外作正方形的顶点为什么一定在格点上。

4.探索直边长不为整数时是否成立

学生提问：边长不为整数时，不便于用格点图形和面积法，a2+b2=c2还成立吗？教师借助几何画板进行验证演示SA+SB=SC，从而完善证明。

5.猜测钝角三角形、锐角三角形时，以上三边关系式是否成立

通过验证强化勾股定理使用的条件是直角三角形。（如图9）

6.以上猜想验证，需要严谨证明

不借助格点图形的勾股定理证法探索，古今中外都有。

（1）“赵爽弦图”证法介绍。

（2）欧几里得证法介绍。

7.公式变式，简单运用

（1）勾股树面积计算。

（2）分类求边：在 Rt△ABC中，已知 a=3，b=4，求c。

（3）直角三角形面积法求高：直角三角形两直边长度分别为6和8，求斜边上高。

（4）勾股法求高：三角形三边长分别为6、7、8，求边6上的高及三角形面积。

（5）“赵爽弦图” 运用练习。

8.拓展延伸

由于勾股定理的特征a2+b2=c2，有的地区也叫作“三平方定理”。边的平方，启发人们的证明思路多与面积有关。请大家课后了解“刘徽证法”等多种证法，以及不用面积证明勾股定理的方法，如射影法等。

二、教学理念的选择与侧重

勾股定理几乎是全世界中学数学课程都要介绍的内容，在数学教育中具有特殊的地位。

（一）从文化的选择看

虽然三种教学中都有数学文化、数学史的渗透，但是选择的时机和重视程度不同。从教学设计的侧重可以看出，三个案例对勾股定理的文化教育目标和德育目标有明显不同。案例一，点到为止，“赵爽弦图”没有发挥激励学生科学探究精神或文化自信的德育功能；案例二和案例三，毕达哥拉斯的探究习惯的榜样作用和“赵爽弦图”的文化自信的德育功能都有一定程度的体现。

教学重点选择不同。案例一的教学重点在运用勾股定理，一节课的三分之二以上的时间是逐步加深各种运用，应试特征明显。案例二的定理推导与运用各占半课时，学生有割补法解决问题的经验积累，但定理的发现仅仅有整数边的情形，存在逻辑上的缺陷。案例三则侧重在定理的发现探究过程，注重逻辑的完整性，不仅有观察习惯的养成教育，而且在定理发现过程中有从特殊（等腰直角三角形）到一般（一般直角三角形）的逻辑完整的探究过程体验，能够培养学生科学研究所需要的严谨精神。

（二）从教学目标分类标准看

案例一，重心在理解、运用上，以低阶思维的培养为主。从现实的课堂成绩测试去看，学生解题适用能力较强，因而是多数教师日常教学的选择。

案例二，有对定理的分析、综合、体验、探究，但是不充分、不完整，流于形式，失去了对学生高阶思维培养的好时机。虽然有割补法的体验，但是从单位时间的教学效果看，属于低效的教学行为。由于练习数量和种类少于案例一，因此估计当堂测试的成绩应该低于案例一。

案例三中定理的发现、猜测、探究、分析、综合的过程是完整的。从方格纸中猜测、验证探索，到不借助方格纸的一般情形的探究，给了学生一次逻辑完整的科学研究的体验，用去整节课超过三分之二的时间，但很有意义，是值得的，因为定理运用的典型性、启发性，落实的时间也足够充分，这节课的测验成绩虽然不会高于前两个方案，但也不会太低。向未来看，学生的可持续发展能力应该好于前两个案例。

更为重要的是，案例三中，教师预设了引导学生反思的两个问题：“斜边外作正方形顶点为什么一定在格点上？非直角三角形有没有类似的结论？”反思习惯的养成，对培养学生的创新能力至关重要。由此可见，案例三关注到了新课标中创新能力培养的高层次目标，是有深度的，是对学生创新力的保护和培育。

宏观审视案例三的教学流程，可以看到，有定理的理解及变式运用，是低阶思维的培养和奠基；案例三再现了科学家善于观察、巧妙利用方格纸工具作出的合理猜想与合作探究，逻辑完整的分析、综合、评价（质疑），有深度地实现了高阶思维能力的培养。割补法的运用体验、从特殊到一般的探究归纳经验，是方法论的培育。数学文化渗透中，学生自主探索的体验、像科学家那样成功获得科学结论的愉悦心情，激发出的民族自豪感、爱国情怀和科学意识，触及学生的心灵。因而这节课的教学具备深度教学的主要特征：深入理解、深度思考，触及心灵的探究精神、科学精神、严谨精神、人文精神。［4］

三、初中数学深度教学的理想

笔者认为，把高阶思维和探究体验作为实现深度教学的阶梯，优化教学过程，可实现理想的课程设计。

关于“四基”。本课的基础知识教学，是勾股定理的理解、记忆、运用。涉及的基本技能包括面积法、割补法、变式法、构造法等，都是解决问题的基本方法和数学工具。涉及的基本数学思想有特殊到一般、一般到特殊、补型思想、数形结合等。数学活动经验是，探索勾股定理的过程，有完整的逻辑链条。

关于“四能”。通过数学家观察地砖的猜想、探索、验证的过程，将发现问题、提出问题、分析问题、解决问题，渗透在教学之中，学生有体验，有感悟，更有自主探究的愿望。毕达哥拉斯做客时所体现的探究習惯，学生需要习得与养成。质疑整数直边时正方形顶点一定在格点的原因，是创新能力的体现。而通过联想、质疑锐角三角形和钝角三角形的结论，也是创新精神的体现。同时，学生也获得了一个认识：证明正确的猜想需要完整逻辑，而证明错误的猜想只需要举反例。这些科学意识和科学精神，属于核心素养和必备品格。

深度教学应该“深”在哪里？从“勾股定理”一课看，深度教学应该“深”在重要的人类文化遗产的传承；应该“深”在体验科学发现的一般过程、自觉意识和理性精神；应该“深”在触及学生心灵深处，涤荡情感，锻造价值观。

从低阶到高阶，强“四基”，提“四能”，更要做好五个重视“活动、合作、思维、感悟、质疑”［4］，这是数学通向深度教学的基本路径。有体验、有感悟，自觉质疑、自觉创新，有情感参与、有人文情怀渗透［5］，触及学生心灵深处，绽放理性精神和科学精神，是数学教育深度教学的航标灯。

【参考文献】

［1］贾保柱.后课改时代人文统整的初中数学教学［J］.中小学数学，2021（12）：1-3.

［2］贾保柱.初中数学突出核心能力教学评价的探索［J］.江苏教育，2015（6）：41-42.

［3］刘月霞，郭华. 深度学习：走向核心素养［M］.北京：教育科学出版社，2018：34-45.

［4］贾保柱.活动，让数学课堂更美好［J］.教育研究与评论，2012（9）：82-85.

［5］贾保柱.人文教育必要的乌托邦［J］.江苏教育，2011（1）：58.