玻璃纤维平纹编织层合板面内剪切渐进失效分析
2023-04-10王轩石强斌高俊福
王轩, 石强斌, 高俊福
(1.中国民航大学航空工程学院, 天津 300300; 2.航空工业济南特种结构研究所高性能电磁窗航空科技重点实验室, 济南 250023)
玻璃纤维平纹编织层合板由径向纤维与纬向纤维垂直交织铺设堆叠而成,具有高比刚度和比强度,广泛应用于飞机雷达罩和发动机机匣等部位[1-4]。这些部位在飞机服役过程中,承受着复杂的载荷,构件易发生拉伸、压缩、弯曲、剪切等变形,其中面内剪切是常见的一种损伤形式,因此研究玻璃纤维平纹编织层合板面内剪切性能具有重要的工程价值。
关于复合材料层合板的面内剪切力学性能研究已经取得了一些成果[5-6]。朱振涛等[7]通过对碳纤维增强复合材料层合板面内剪切试验结果的统计分析,得到了分散性模型的具体表达式,并给出了材料性能的分散性模型参数。Strungar等[8]在Iosipescu试验中考虑三维编织复合材料的结构特征,对其剪切性能进行实验研究,采用应变和位移场对面内剪切进行评估。Dayou等[9]基于多尺度数值模拟,在不同的加载方式下,对芳纶纤维编织复合材料和玻璃纤维编织复合材料的力学特性进行了研究,表明纤维束结构的不确定性对复合材料的面内剪切性能有显著的影响。Jia等[10]针对由单向带组成的厚截面复合材料,建立了一种多尺度渐进损伤分析方法预测面内剪切的失效模式。王童童[11]利用微计算机断层扫描技术对三维编织复合材料建立几何模型,预测面内拉伸性能和面内剪切性能。赵琳等[12]基于单胞解析模型,建立一种从细观到宏观的复合材料面内剪切性能和损伤的分析方法,发现面内剪切的应力应变曲线具有非线性。目前的面内剪切性能研究中,缺少考虑非线性本构的平纹编织层合板渐进损伤失效过程研究,难以精确预测平纹编织层合板面内剪切失效。
与常见的单向带不同,平纹织物由于经向纤维和纬向纤维的存在,它的力学性能、损伤模式和损伤机理都会有所不同。现针对玻璃纤维平纹编织层合板,基于V形开口梁面内剪切试验数据,建立Ramberg-Osgood非线性剪切本构模型,采用ABAQUS有限元软件和VUMAT子程序建立其渐进损伤失效分析模型,预测其面内剪切力学性能和损伤起始-扩展全过程,揭示其面内剪切失效机理。
1 渐近失效分析模型
1.1 面内剪切非线性本构模型
与各向同性的材料不同,层合板由于树脂这一组成成分的存在,在进行剪切性能研究时必须考虑材料的非线性黏弹性。本文研究中采用Ramberg-Osgood本构方程来表示剪切非线性。文献[10,12-13]采用应力应变关系建立本构模型描述剪切非线性,模型精度取决于试验测得的应力应变数据的精确程度,然而试验测得的数据往往因为各种原因导致结果有较大的分散性。相比较应力应变数据而言,位移载荷数据比较容易获得,精度比较高。因此本文研究根据位移载荷曲线,结合Ramberg-Osgood模型,来描述面内剪切非线性,本构方程为

(1)

(2)
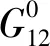
1.2 失效准则
平纹编织层合板相对较薄,因此只考虑经纬方向上的力学性能,而忽略垂直于面板方向的力学性能。结合试验结果,预测分析模型中只考虑径向纤维拉伸和压缩失效、纬向纤维拉伸和压缩失效和纤维-基体剪切失效,共5种损伤模式。
参考二维Hashin失效准则以及Tsai-Hill失效准则,得到了平纹编织层合板失效准则的表达式[14],如式(3)~式(7)所示。
纬向纤维拉伸失效(σ11>0)为

(3)
纬向纤维压缩失效(σ11<0)为

(4)
经向纤维拉伸失效(σ22>0)为

(5)
经向纤维压缩失效(σ22<0)为

(6)
纤维-基体剪切失效为

(7)
式中:XT为纬向纤维的拉伸强度;YT为经向纤维的拉伸强度;XC为纬向纤维的压缩强度;YC为经向纤维的压缩强度;S12、S13、S23分别为单层板各方向面内剪切强度;σ、τ分别为正应力、切应力;下标的数字1、2、3分别为层合板的纵向、横向和厚度方向。
1.3 刚度退化准则
在文献[15]中参数退化准则的基础上,建立的玻璃纤维平纹编织层合板的参数折减方式如表1所示。

表1 平纹编织面板面内剪切下材料性能退化系数
1.4 有限元模型
基于ABAQUS有限元软件模拟平纹编织层合板面内剪切渐进失效过程,建立面内剪切有限元模型,如图1所示。将模型设为三维8节点实体单元(SCD8R),采用减缩积分,沙漏控制。在模型的右上侧表面建立一个参考点RP-1,采用equation的约束方法,将右侧上表面与参考点RP-1的连接在一起,并将位移载荷施加在参考点上,模型的左侧采用完全固定的方法,约束方式如图2所示。模型的失效区域主要在V口区域,所以将此区域的网格加密,用来提高计算精度,节约计算时间。采用ABAQUS/Explicit求解器对所建立的模型进行模拟计算。玻璃纤维平纹编织单层板的工程常数如表2所示,相关的强度参数如表3所示。

图1 试验件有限元模型Fig.1 Finite element model of test piece
图2 模型约束方式Fig.2 Model constraint mode

表2 玻璃纤维平纹编织单层板工程常数

表3 玻璃纤维平纹编织单层板强度参数
基于材料的本构方程、非线性模型、失效判据、损伤模式和失效后的刚度退化准则,编写了VUMAT子程序,进行面内剪切渐进损伤失效分析。利用VUMAT求解时会从ABAQUS读取单元的应变值,用更新的应变值结合非线性本构方程计算剪切模量,然后用刚度矩阵来计算应力值,用得到的应力值进行本构方程的计算,并判断单元是否达到失效状态。达到失效状态的单元用衰减过的刚度进行应力计算,没有失效的单元用初始刚度矩阵计算应力值。在更新完状态变量后,将此值传递给ABAQUS,在位移载荷的加载下往复循环,直到完全失效或者达到指定位移,建立的渐进损伤失效模型计算过程如图3所示。

图3 渐进失效分析流程图Fig.3 Flow chart of progressive damage analysis
2 试验
平纹编织复合材料层合板面内剪切试验参考美国材料与试验学会(American Society for Testing and Materials,ASTM)D5379/D5379M[16]标准进行试验,试验件数量为7个。面内剪切试验件尺寸如图4所示,试验件材料为7781型玻璃纤维平纹织物增强PR381环氧树脂基。试验件单层名义厚度为0.26 mm,层合板的总厚度为厚3.12 mm。单层板纤维铺设方式为经度纤维与纬度纤维垂直铺设,各层织物铺设角度均为0°,沿厚度方向堆叠12层。本次试验采用Instron 5982 电子万能材料试验机进行玻璃纤维平纹编织层合板剪切性能试验,加载速度设置为0.5 mm/min,环境温度为(25±3) ℃,试验夹具采用ASTM D5379/D5379M标准中规定剪切夹具。在进行面内剪切试验时,为了防止试验件扭转带来的影响,需同时测量试验件两侧的两个应变元件,以便对试验件的任何扭转进行校正。采用电阻应变片来测量应变,以试件V口处的中截面为参考轴,安装在加载轴的+45°和-45°处。

图4 面内剪切试验件尺寸Fig.4 Dimension diagram of in-plane shear test piece
3 结果分析
3.1 面内剪切强度
面内剪切的试验结果如表4所示,参考ASTM D5379/D5379M标准,用试件承受的最大剪切载荷Pu表示面内剪切强度,面内剪切初始模量,计算公式为

(8)
式(8)中:Gchord为线性阶段的剪切模量;Δτ为两个应变片之间的应力差值;Δλ为两个应变片之间的应变差值。
试验结果的变异系数的计算公式为

(9)

(10)

(11)
如表4所示,面内剪切强度和剪切模量变异系数均小于10%,变异系数小于15%,试验结果工程上可以接受。
为了对玻璃纤维平纹编织层合板面内剪切强度的试验值与预测值之间的进行对比,选择用相对误差(relative error)进行有效评估,计算公式为

(12)
式(12)中:d1为相对误差;n为试验件数量;Fi为各试验件测试载荷强度值;F0为预测载荷强度值。
图5为面内剪切最大载荷试验与预测结果对比图,其中仿真预测值为3.48 kN,对比试验得到的平均值,相对误差为9.50%,说明预测值与试验值比较吻合。

表4 面内剪切性能试验结果

图5 面内剪切试验强度预测结果与试验结果对比Fig.5 Comparison between strength prediction and test results of in-plane shear
3.2 位移载荷曲线
图6为层合板面内剪切试验件位移载荷曲线,整个曲线呈现非线性。从图6中可以观察到,试验件在加载初期即I区域内,位移载荷曲线近似线性,试验件在该阶段表现为线弹性[17]。在II区域开始时,曲线的斜率发生明显的变化,除了与非线性的特性有关外,还与刚度的折减有关;当施加载荷约为1.8 kN时,伴有清晰响声,说明试验件内部纤维断裂,此时试验件两侧与夹具接触处表面也观察到损伤。随后,位移载荷曲线开始比较平缓地上升,在上升到III区域内时,曲线发生明显的折减,斜率逐渐的变为负值,说明试验件产生的损伤导致材料属性由微小损失过渡到大幅折减。结合图8的最终的失效模式可以看出,在V口处(I)有明显的因纤维拉伸断裂产生的损伤,与夹具的接触处有明显的压溃损伤(II),在试验件背面(III)可以观察到波纹状的裂纹以及明显的错位现象。
3.3 面内剪切模量


(13)

表5 Ramberg-Osgood模型拟合参数
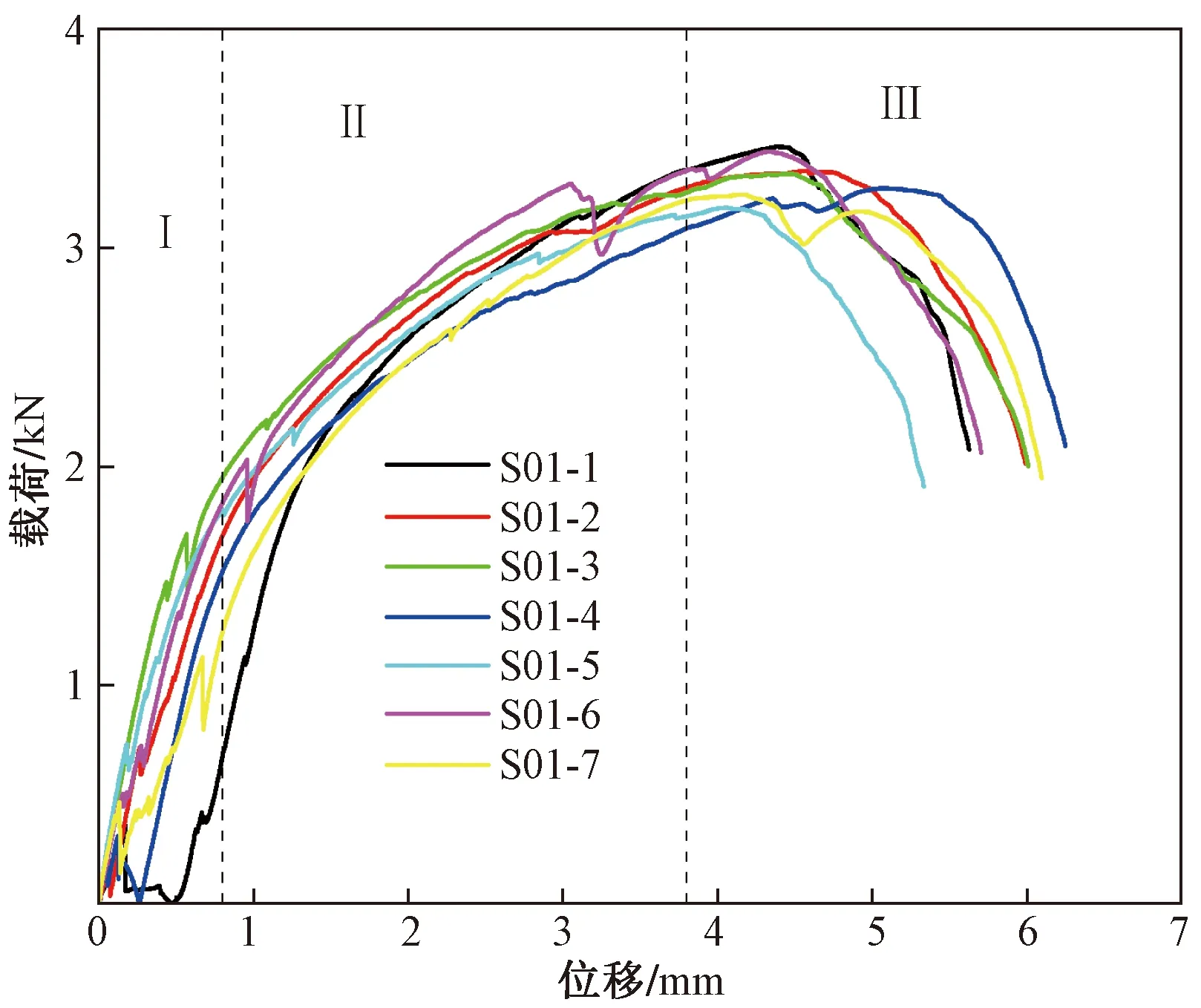
图6 面内剪切试验件剪切位移载荷曲线Fig.6 Shear displacement load curve of in-plane shear test piece
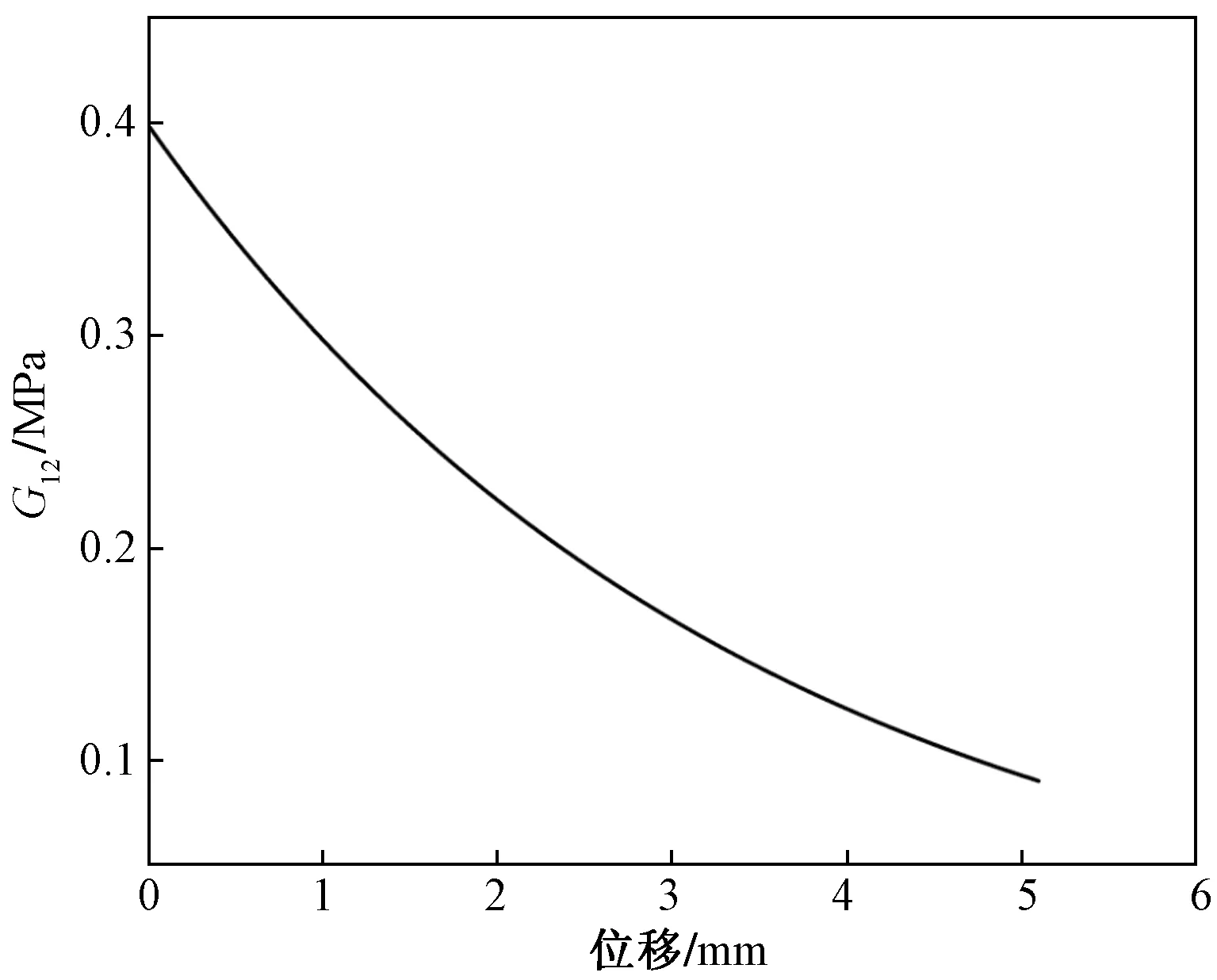
图7 剪切模量变化图Fig.7 Variation of shear modulus

图8 面内剪切试验件试验破坏模式Fig.8 Failure modes of the undamaged test pieces

图9 面内剪切试验和仿真位移载荷曲线对比Fig.9 Comparison of in-plane shear test and simulated displacement load curve
3.4 渐进损伤失效过程
通过观察试验件的破坏模式,发现沿着V口的竖直方向出现断裂破坏,试验件在V口处有明显的变形破坏,而且产生的裂纹为多角度的混合,是ASTMD5379/D5379M标准给出可接受的面内剪切破坏模式。根据有限元软件对子程序进行的定义,其渐进损伤失效模式共包含5种[18-19],分别为SDV1纬向纤维拉伸失效、SDV2纬向纤维压缩失效、SDV3经向纤维拉伸失效、SDV4经向纤维压缩失效、SDV5纤维-基体剪切失效。根据面内剪切试验最终失效仿真破坏结果可以发现,不同方向纤维所受到的拉伸、压缩和剪切破坏各不相同,且失效发生的顺序也不相同,主要失效模式体现在经纬向纤维的拉伸、压缩以及纤维-基体的剪切破坏,因此将对这3种损伤扩展进行对比分析。
通过试验和仿真可以得到,剪切实验主要的损伤区域在试验件的V口区域附近,为了更直观地对损伤过程进行展示,选取试验件V口附近区域来展示各种失效状态。图10为各种损伤模式随着分析步时间的变化图。在SDV1所指示的纬向纤维拉伸损伤中,损伤从分析步时间为0.32时开始产生,往后随着分析步时间的增加,损伤区域也在逐渐增加;从损伤位置可以发现,面内剪切纬向纤维拉伸损伤破坏首先发生在V口底部从左上到右下的对角区域,然后沿着V口中垂线发生贯穿失效,并沿着对角区域向外延伸,直至整个V口面内大面积失效。在SDV2所指示的纬向纤维压缩损伤中,当分析步时间为0.55时损伤开始出现,比拉伸损伤出现的时间晚0.2的分析步时间,之后随着分析步时间的增加,损伤区域也逐渐扩展;纬向纤维压缩损伤起始位置位于V口槽右上至左上的尖端处,随着分析步时间的推进,损伤区域逐渐增大,但是最终产生的损伤区域相对拉伸损伤来说较小。
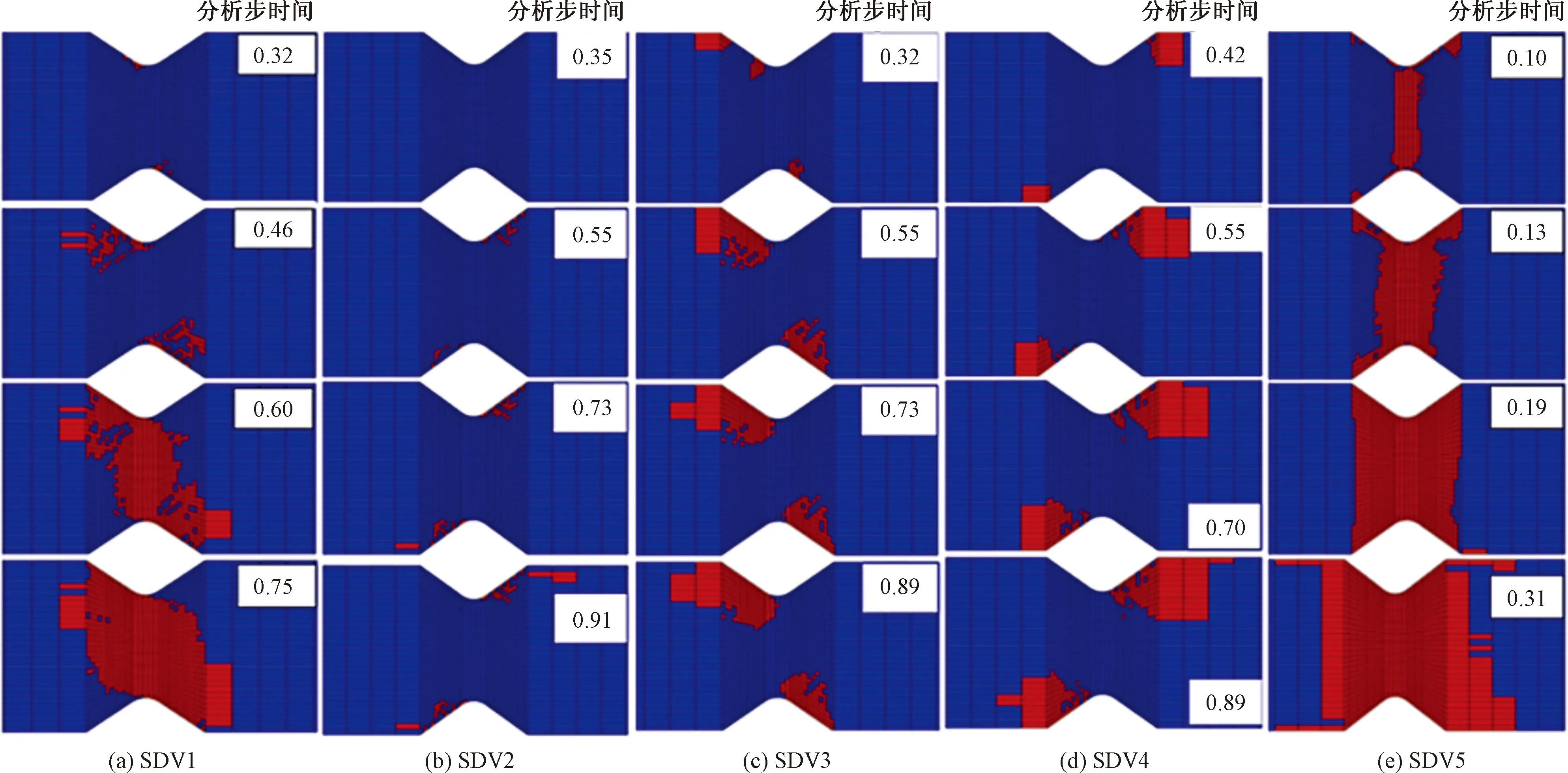
红色代表材料达到失效状态图10 损伤模式随分析步时间的演化Fig.10 Evolution of damage mode with time of analysis ste
在SDV3所指示的经向纤维拉伸损伤中,损伤从分析步时间为0.32时开始扩展,往后随着分析步时间的增加,损伤区域也在逐渐增加;从损伤位置可以发现面内剪切经向纤维拉伸损伤破坏首先发生在V口的左上顶角和槽口底部的左上至右下对角处,然后沿着对角失效区域逐渐增大,中部没有发生贯穿损伤。在SDV4所指示的纬向纤维拉伸损伤中,当分析步时间为0.42时损伤开始出现,这个时间比纬向压缩损伤出现的时间早一点,但是比经纬向纤维拉伸失效出现的时间晚,之后随着分析步时间的增加,损伤区域也逐渐扩展;因为材料与夹具施加载荷的位置相接触,此处的所承受的压力较大,所以经向纤维的压缩失效首先发生在靠近V口顶角与材料接触的区域,然后沿着右上至左下的对角向V口中心延伸,但是最终产生的损伤区域相对拉伸损伤来说较小,没有贯穿整个V口区域。
在SDV5所指示的纤维-基体剪切损伤中,在分析步时间为0.10时就发生了剪切损伤,损伤的初始位置在V口槽右上侧边缘处和V口的中间区域,之后随着分析步的增加,损伤区域逐渐增大;在分析步时间为0.2左右时,整个V口区域发生了剪切损伤,之后随着分析步时间的增加,剪切损伤延伸到了非V口区域。
综合所有的损伤分析,从分析步时间的对比可以得到,剪切损伤发生的最早,扩展速度也是最快的,之后发生经纬向纤维的拉伸损伤,然后是经向纤维的压缩损伤,最后发生的是纬向纤维的压缩损伤[20]。模拟得到的损伤结果结合层合板黏弹性的因素,很好地解释了面内剪切试验呈现非线性的原因,与实验达到了良好的吻合,验证了所建立的有限元模型的正确性。
图11为面内剪切应力云图,发现在加载初期V口4个尖端区域立刻表现出应力集中的现象,随着载荷的增加,V口中心区域的应力迅速增大,因此此处是最先失效的位置,而后应力集中在V口的4个尖端区域中扩展,其中右上至左下的对角区域应力集中最大,表现为纬向纤维拉伸失效。图12代表临界应力图,T区域[21]所预测的断裂面上的正应力大于零,潜在的临界失效模式为拉剪失效;C区域所预测的断裂面上的正应力小于零,潜在的临界失效模式为压剪失效。从分析步时间的推进来看,应力正负变化最大的区域主要为V口区域,在右上至左下区域,初始应力为压应力,随着载荷增大,该区域应力变为负值。整个模型应力分布为:右上至左下为压应力,左上至右下为拉力,这与位移载荷的施加方式有关。
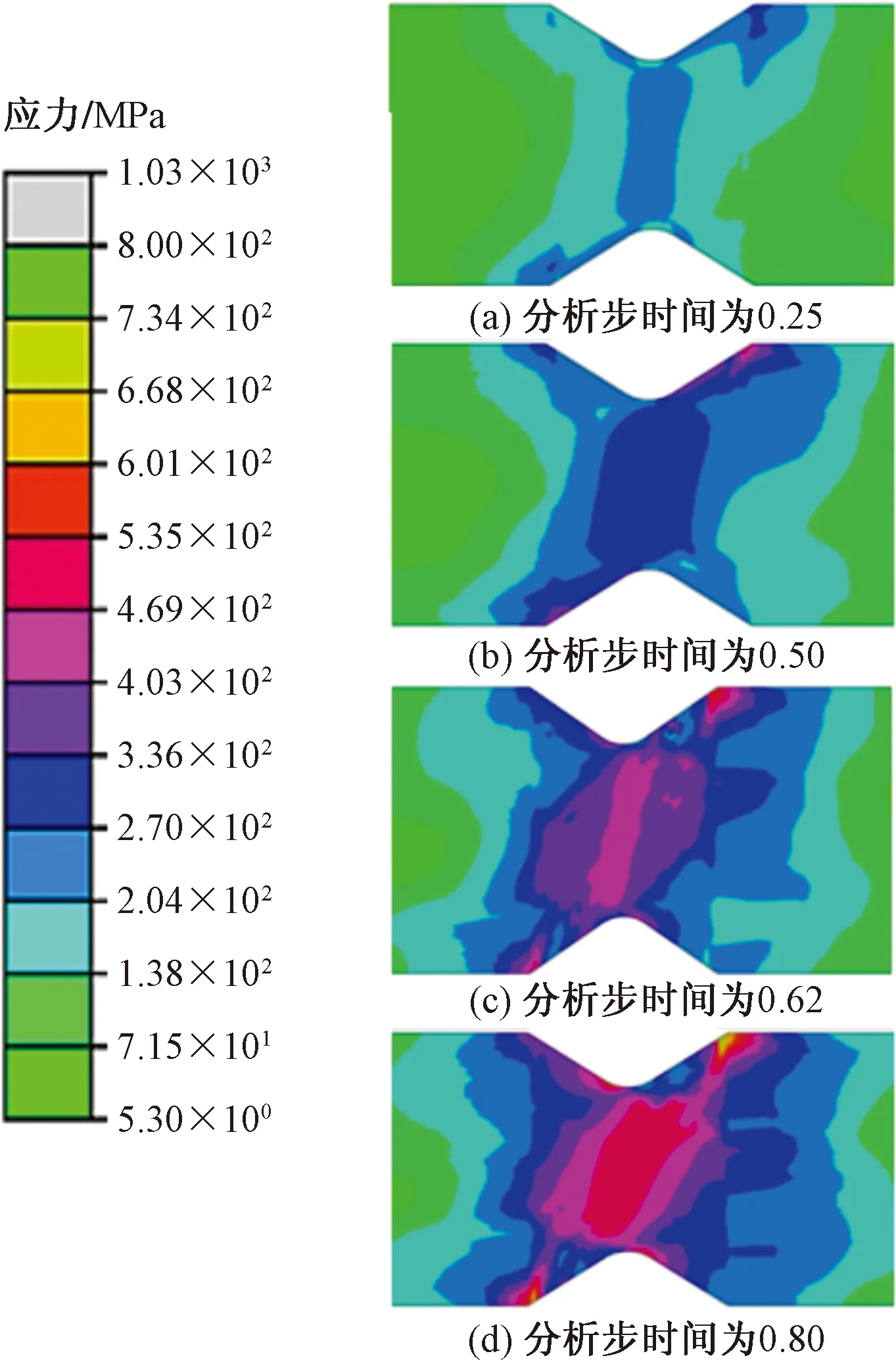
图11 仿真模型的应力云图Fig.11 Stress nephogram of simulation model

图12 仿真模型的应力临界图Fig.12 Critical stress diagram of simulation model
4 结论
(1)通过面内剪切试验,得到了玻璃纤维平纹编织层合板的面内剪切强度和初始剪切模量,试验值和预测值与试验吻合较好。
(2) 建立Ramberg-Osgood模型,可以较好地表达面内剪切非线性,仿真分析得到的位移载荷曲线与试验结果之间的吻合较好。
(3)玻璃纤维平纹编织层合板在面内剪切过程中,纤维-基体剪切损伤发生的最早,扩展速度也是最快的,之后依次发生经纬向纤维的拉伸损伤,然后是经向纤维的压缩损伤,最后发生的是纬向纤维的压缩损伤。模拟得到的结果可以和实验达到良好的吻合,进一步验证了所建立的有限元模型的正确性。
