基于图形相似度的分布式能源接入配电网差动保护方案

卫泽喆, 武家辉*, 张华, 杨健

(1.新疆大学电气工程学院, 乌鲁木齐 830047; 2.可再生能源发电与并网控制教育部工程研究中心, 乌鲁木齐830047;3.中广核新能源投资(深圳)有限公司新疆分公司, 乌鲁木齐 830011)

随着国家能源战略转型,建设以新能源为主导的新型电力系统,成为电网建设发展的主要方向。传统配电网其拓扑结构和故障特征将随着高渗透率分布式电源的接入而变得更加复杂,传统继电保护的配置已无法满足日益复杂的配电网系统,配电网的安全运行将受直接影响。

分布式电源(distributed generation,DG)类型多样,按照其与配电网并网接口可分为经换流器并网的逆变类(inverter interfaced DG,IIDG)和直接并网的旋转电机类(motor type DG,MTDG)[1]。IIDG受其控制策略影响,故障时短路电流最大只能达到额定电流的1.2～2倍[2],如果以IIDG为主电源的配电网发生相间故障,主变压器侧的故障电流与DG侧测量的故障电流将不在同一数量级[3]。当MTDG接入配电网时,故障时输出电流可达5～7倍[4]。这些因素使得含分布式电源配电网保护的整定方案变得更加困难,分布式电源的发展受到严重制约。

针对上述问题,中外学者进行了多方面探讨,主要包括限制DG接入容量、传统保护方法的改进、利用5G等新型通信技术。文献[5]以阶段式电流整定值为约束,计算了最大允许分布式光伏电源接入容量。文献[6]依据零序电流与中性点电流pearson相关性构建接地防护方案。文献[7]利用相邻开关站电压幅值误差构建保护判据,对故障区域进行了判断并隔离。文献[8-9]以中性点电压和负序电流为保护特征量,可以准确识别单相断线故障。文献[10]线路差动保护方法基于5G和光纤综合通道构建,降低了对通道的要求,实现了综合通道差动保护的同步。文献[11]提出了一种改进的数据自同步算法,利用电流过零时间和电流斜率极性来估计两端的启动延迟差,提出了相应的差动保护方案。

在多电源网络中,考虑到电流差动保护具有良好的选择性和速动性[12-13],一些学者在含DG配电网的保护中引入电流差动保护。文献[14]分析了不同类型分布式电源故障时正序电流的差异,动作量由线路两端正序电流幅值比构建,制动阈值由相位差构建。文献[15]通过利用故障分量幅值传输,采用正序电流幅值比构造幅值保护判据。文献[16]分析了当发生故障时,接线方式为T型接线的配电网多端电流间幅值和相位之间的关系,提出包含启动判据和复合动作判据的保护方案,但上述方法对线路两端信息的同步的要求较高。文献[17]利用正、负、零序电流,构建了完整的综合序电流比保护方案,但它只适用于不太重要的中低压配电网。因此进一步研究一种对通信要求较低,且不需要添加新保护装置的保护方案具有重要的理论和实践意义。

Hausdorff距离算法是一种计算图形相似度算法。近年来,已经有研究人员将其应用在故障定位、故障选线、变压器保护等方面[18-21]。现将Hausdorff距离算法与配电网差动保护相结合,阐述Hausdorff距离算法的基本原理,深入研究分布式电源接入配电网发生不同类型故障时Hausdorff距离变化情况,提出一种利用电流波形特征,基于Hausdorff距离算法的差动保护方案。最后在PSCAD/EMTDC软件上搭建含分布式电源配电网模型进行验证。

1 Hausdorff距离基本原理

Hausdorff距离用于测量给定欧氏空间中的两组点A={a1,a2,…}、B={b1,b2,…}之间的距离,并描述作为一个整体之间两组点的最大不匹配程度,Hausdorff距离与两组点之间的最大不匹配程度成正比关系,Hausdorff距离越大,两组点之间的最大不匹配程度就越大。公式定义为

H(A,B)=max[h(A,B),h(B,A)]

(1)

式(1)中:

(2)

(3)

式中:|a-b|为两组点A和B之间任意两点间的欧几里得距离;h(A,B)称为从点A到点B的单向Hausdorff距离,依此类推,h(B,A)称为从点集B到点集A的单向Hausdorff距离。计算求解过程包括求解单向距离中h(A,B)、h(B,A)中最小值,然后将单向距离的两个最小值之间的最大值取为H(A,B),H(A,B)称为双向Hausdorff距离。

Hausdorff距离用来计算两组点之间的欧氏距离,反映其两组点之间的整体相似性,两组点之间的细微差别将被忽略,H(A,B)越小,表明两组点间相似性越大。因此,Hausdorff距离算法可以反映两组波形之间的差异程度,而在电流差动保护中,使用的电流信息来自线路两端电流互感器的采集二次电流,考虑采用线路两端的时间信息和电流幅值特性来构造两组点,每一个数据点都可以用作图形的某个特征点来计算两端电流的Hausdorff距离,然后将其与差动保护相结合,提出一种利用两端电流波形特征,基于Hausdorff距离算法的差动保护方案。

2 基于图形相似度的自适应差动保护方案研究

2.1 含DG配电网故障电流与Hausdorff距离分析

当线路发生区内、区外故障时,理论上故障电流在波形上会有较大的差别。以图1所示的含DG配电网简易模型为例说明发生区内外故障时的电流波形特征。

图1 含DG配电网简易模型Fig.1 Simple model of distribution network with DG

Hausdorff距离算法本质上是对波形相似度进行实时计算,所以数据窗大小不影响动作速度。理论上数据窗大小可以任意设定,不影响计算。区别在于当数据窗过长时,采样点数多,计算量大,计算值输出平稳且受异常数据影响小;当数据窗过短时,计算量小,计算值输出更能反映波形变化信息。综合考虑选择性与速动性,选择5 ms作为数据窗。

当线路发生不同区域故障时,线路两端的A相电流波形与Hausdorff距离值变化情况如图2所示。

H为Hausdorff距离;I为母线两端电流;t为时间图2 不同故障下Hausdorff距离变化情况Fig.2 Variation of Hausdorff distance under different faults

2.2 基于Hausdorff距离的差动保护原理

H>Hset

(4)

式(4)中:H为一个数据窗5 ms内实时的Hausdorff距离值;Hset为固定门槛值,综合考虑如图2所示的区外故障与区内高阻故障时Hausdorff距离值,Hset取0.05。当式(4)满足时,差动保护方案可靠启动。

借鉴向量和差比率制动判据[22],提出以下差动保护判据:

(5)

式(5)中:

(6)

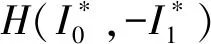
图3 保护动作原理与流程图Fig.3 Protection action principle and flow chart

Iact>IOP

(7)

令

(8)

式中:Iact为动作电流,当动作电流大于启动门槛值时,保护动作。

与传统的比率制动式差动保护相比,制动系数典型取值范围在0.5～0.8,一般为固定值,这种取值不能平衡速动性与可靠性。本文提出的差动保护方案可以根据Hausdorff距离值而改变制动系数K,从而改变保护动作范围,在最大范围内保护线路安全。

2.3 保护方案

基于Hausdorff距离的差动保护方案的保护动作原理和流程图如图3所示。首先通过智能电子设备(intelligent electronic device,IED)记录电流互感器(current transformer,CT)采集到的实时电流数据,然后进行同步与归一化处理,利用处理后线路两端电流计算Hausdorff距离,当满足启动判据H>Hset时,实时构建制动系数K,并根据比率差动保护判据进行区内故障判别。

3 仿真与验证

为了验证所提出方案的有效性,基于仿真软件PSCAD/EMTDC建立了如所图4所示的配电网模型,利用MATLAB软件进行保护方案的验证。

图4 含分布式电源的配电网模型Fig.4 Distribution network model with distributed generation

其中节点模型采用标准节点模型IEEE33,中性点经消弧线圈接地,电感值为0.3 H,消弧线圈补偿度为10%,为小电流接地系统。在节点0接入三相电源,容量为100 MW,分布式电源在节点17、21、24处接入,分为IIDG和MTDG两种类型,其中DG2是光伏发电系统,为IIDG类型,容量为0.25 MW,控制策略采用PQ控制,DG1和DG3分别为风电场和燃气轮机,为MTDG类型,容量分别为0.65 MW和0.4 MW。在下文的仿真分析过程中,均以A相为例进行故障电流分析,故障时刻均设在1.1 s,故障持续时间为0.5 s。

3.1 不同故障区段

为了进一步验证本文所提方案的选择性,以线路4-5两端保护动作为例,模拟线路3-4(区外),4-5(区内)发生不同类型故障时线路4-5保护动作情况与Hausdorff距离的变化情况。传统电流差动保护制动系数K取值为0.5。如图5(a)所示,黑色实线与红色实线分别为传统保护方案与新型保护方案,线路4-5(区内)在1.1 s发生三相接地故障,在发生故障后的下一个数据窗Hausdorff距离迅速升高,越过门槛值Hset,保护方案可靠启动,动作电流Iact大于门槛值Iop,跳闸信号发出,保护准确动作。两种保护方案均可以动作,但文中所提保护的结果大于传统保护,具有更好的灵敏度。如图5(b)和图5(c)所示,线路3-4(区外)1.1 s发生三相故障和BC两相接地故障时,Hausdorff距离始终小于门槛值,动作电流Iact也始终小于门槛值Iop,两种保护方案均可靠闭锁。

图5 不同位置故障时线路4-5动作电流与Hausdorff距离变化情况Fig.5 Change of line 4-5 operating current and Hausdorff distance in case of fault at different positions

当其他线路(区外)故障时,仿真结果与上述4-5线路发生故障类似,不满足启动判据,动作电流Iact始终小于门槛值Iop,保护始终闭锁,在此不再赘述。

3.2 不同DG类型

该保护方案基于线路两端电流相似度构建差动保护方案,为了研究不同类型DG接入配电网对线路两端电流Hausdorff距离的影响,验证不同类型DG接入时保护的可靠性与灵敏性,通过线路18-19、23-24、25-26模拟MTDG、IIDG、无DG 3种情况接入配电网,线路中发生三相接地故障时各区段保护动作结果如表1所示。可以看出,无论是哪种类型DG接入配电网,两种保护均可在三相接地故障时动作,但是本文所提的方案在故障后第一个数据窗内,式(4)得到满足,保护可靠启动,式(7)成立,保护动作,传统保护则在第二个数据窗时才满足动作条件。因此,本文所提的差动保护方案在不同类型接入配电网时发生三相故障均可准确识别区内故障,而且具有更好的速动性。

表1 线路发生三相接地故障Table 1 Three phase grounding fault of the line

配电网系统中性点经消弧线圈接地,补偿度为过补偿时,系统为小电流接地系统。在单相接地故障的情况下,故障点接地电流为补偿后的残余感性电流,该值较小,因此可以允许带故障运行1～2 h[23]。

表2给出线路发生A相接地故障后0.005 s和0.010 s时的仿真结果。由于电流数值较小,传统差动保护不能准确动作。本文所提的保护方案虽然在两端电流波形的差异性较小,但Hausdorff距离与动作电流仍然在第一个数据窗内大于门槛值,故障区内保护可以准确动作。随着过渡电阻阻值的增加,故障区段的Hausdorff距离也将减小,达到动作电流超过门槛值的时间也将增加。如果过渡电阻进一步增大,这时就需要专门的高阻故障选线方案进行判别。

由上述分析可以得出,本文所提的保护方案在不同类型的DG接入配电网时均可适用,并在不同故障类型下具有良好的性能。

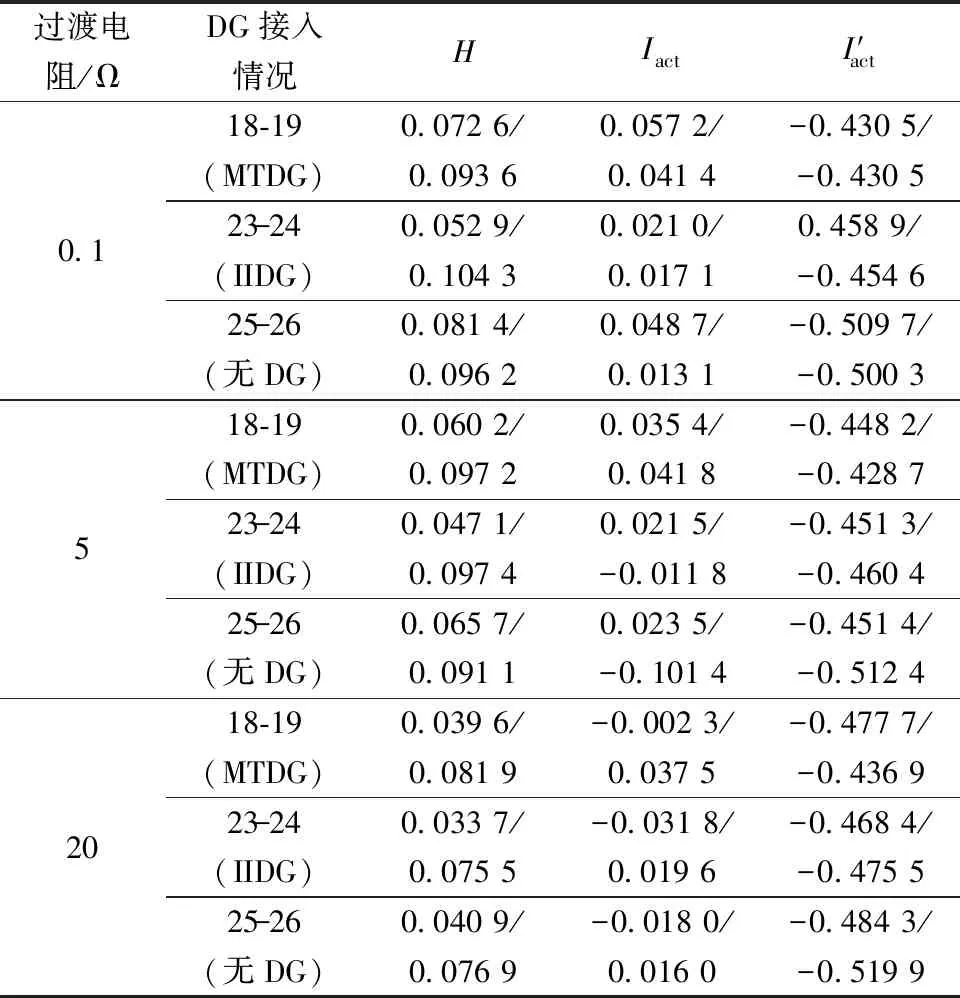
表2 线路发生A相接地故障Table 2 Phase a grounding fault occurs in the line

仿真结果表明,传统保护方案在发生单相故障时不能准确识别故障,而本文所提的保护方案在DG的接入容量发生改变时,线路两端电流的相似度和动作电流均无明显差异,保护动作范围不受DG接入容量的影响,可以在不同容量、不同类型故障下准确识别区内故障。

3.3 线路两端数据不同步

差动电流保护对涉及的两侧电气量的采样时间有很高的要求,但是在数据采集、数据传输过程中难免会造成数据的不同步,影响保护的准确动作。因此,仿真分析某一端电流数据延迟造成两端时间不同步对保护的影响情况。

图侧延迟2 ms动作电流与Hausdorff距离变化情况Fig.6 Change of action current and Hausdorff distance at side with delay of 2 ms

3.4 不同过渡电阻

为了验证区内经过不同过渡电阻发生故障时,所提保护方案是否可靠动作,在22-23线路中模拟三相经过不同大小过渡电阻接地故障时,传统电流差动保护与本文所提的保护方案的动作电流Iact如图7所示,传统电流差动保护制动系数K取值为0.5。点划线与实线分别为传统保护方案与新型保护方案,划线为门槛值。

图7 经不同过渡电阻发生三相接地故障时仿真结果Fig.7 Simulation results of three-phase grounding fault through different transition resistance

可以得出,在传统差动保护中,动作电流随着过渡电阻的增加而减小至小于门槛值,保护无法正确动作。而本文所提出的差动保护方案在过渡电阻不超过20 Ω的情况下,动作电流Iact均超过门槛值,保护准确动作,本文所提的保护方案具有良好的抗过渡电阻能力。

4 结论

为应对分布能源接入配电网给传统保护带来的影响,提出了一种基于Hausdorff距离的配电网差动保护方案。所提方案利用线路两端电流求取Hausdorff距离,当超过设定阈值时,利用距离值构建新的比率差动保护的制动系数,借鉴传统比率差动保护判别线路区内外故障。通过本文理论分析、仿真验证,可得出以下结论。

(1)本文提出的方法动作性能良好,不受DG接入类型、故障位置、故障类型的影响,均可以准确识别区内故障。

(2)本文所提方法具有较强的耐过渡电阻能力,在过渡电阻不超过20 Ω的范围能均可准确动作。此外,此方案具有较好的抗同步误差能力,线路两端电流在一定范围内出现同步误差时,所提方法可以保证在区内故障时正确动作,区外故障时保护可靠闭锁,此外5 G等新型技术的普及,较好地解决了同步问题。

(3)本文所提方法仅仅利用线路两端电流幅值,不需要两端电压信息,判据构建简单,对通信要求不高,同时兼容了低成本与高可靠性。但是在配电网谐振系统中,发生单相故障时消弧线圈对电容电流的深度补偿作用后,残余故障电感电流数值较小,相似度差异不够明显。因此,后续将进一步研究在谐振配电网系统中,发生单相故障时的故障定位与故障选线,进一步完善分布式能源接入配电网时的保护方案。