基于二次分解NGO-VMD残差项与长短时记忆神经网络的超短期风功率预测

2023-04-10宋江涛崔双喜刘洪广

科学技术与工程 2023年6期

宋江涛, 崔双喜, 刘洪广

(新疆大学电气工程学院, 乌鲁木齐 830047)

近年来,随着人们生活质量不断提高,使得能源消耗也逐日增加,同时生态环境也受到了严重的破坏,所以必须寻找新的清洁能源代替化石能源去缓解这一现象[1]。风能为一种环境友好型的绿色能源,其丰富的储能让它在各国得到了快速的发展。然而,风能受气象和环境等因素的制约,使得风力发电呈现出波动与随机等特点[2],这影响了电网对风电的调度,阻碍了风能的发展。目前,对风电功率的精准预测是帮助运行人员实现合理的风功率规划和实时调度,保证电力系统可靠运行的重要方向[3-4]。现如今,超短期风功率预测方法大致可以分为物理方法、时间序列方法、人工智能方法三大类[5-6]。物理方法主要是利用气象数据和地面物理信息计算风电机组轮毂高度的风速大小与风向等信息。通过物理方法预测风功率不需要风电场的历史数据,但其预测精度高度依赖气象数据[7],由于气象数据往往更新较慢,这导致物理方法预测精度较低。

时间序列法指只采用历史功率数据来预测未来的功率数据的方法。时间序列法有:持续法、自回归滑动平均法[8]等。时间序列方法虽然简单,但其未考虑气象因素,当气象变化剧烈时,其预测精度会随时间的增加而降低。

人工智能是目前研究的热门领域,其通过不同的人工智能方法找出功率影响变量和输出功率之间的非线性映射关系。人工智能法主要包括极限学习机(extreme learning machines, ELM)[9]、支持向量机(support vector machine, SVM)[10]、人工神经网络(artificial neural network, ANN)[11]等。文献[12]为解决风功率预测过程存在过学习等问题,提出将支持向量机(SVM)应用于风功率预测,取得了较好的结果,但该方法应用于大规模数据时结果并不理想。文献[13-14]采用长短时记忆神经网络(long short-term memory, LSTM)和其他机器学习模型作对比,结果表明LSTM预测精度更高,但如果输入LSTM的数据质量参差不齐时,其预测精度明显下降,需要组合其他相关技术进行改善。文献[15]提出了一种基于经验模态分解(empirical mode decomposition, EMD)与LSTM组合预测方法,先用EMD对原始序列进行分解,将其再作为LSTM的输入进行预测,该方法有效提高了LSTM的预测精度,但EMD容易产生模态混淆的现象。文献[16]提出了变分模态分解(variational mode decomposition, VMD),该分解方式能够有效解决EMD模态混淆的问题,但其效果与参数设置密切相关。文献[17]采用麻雀搜索算法对VMD的参数进行寻优,并对各子模态采用不同LSTM参数分别进行预测,取得良好的预测效果。

为了充分挖掘数据信息,提高预测精度,许多学者尝试研究二次分解技术。文献[18]先采用快速集合经验模态分解(fast ensemble empirical mode decomposition, FEEMD)[19]将风功率分解后,对其分解后的高频模态采用VMD进行二次分解,有效提高了预测精度。文献[20-21]均对分解后复杂程度较高的前几个模态分量进行VMD二次分解。试验表明二次分解技术的组合预测模型的预测精度较EMD、VMD等一次分解模型得到了很大提升。但目前使用变分模态分解(VMD)搭建的单次分解组合预测模型中,大多均直接忽略了风功率经VMD分解后残差项,在二次分解风功率组合预测模型中都未对分解后的残差项进行二次分解,其都忽略了残差项所包含的丰富信息。

鉴于以上问题和结论,现提出一种基于二次分解NGO-VMD残差项与LSTM的超短期风功率组合预测模型;首先,使用北方苍鹰优化算法(northern goshawk optimization,NGO)[22]对VMD的参数进行寻优,以选出最佳VMD参数组合;其次,采用NGO-VMD模型对VMD残差项进行二次分解,利用K均值聚类算法解决VMD分解模态分量个数多,计算量繁冗的问题;最后,建立LSTM模型对各子模态分别预测并叠加各子模态的预测值得到超短期风功率预测结果。通过对新疆某风电场的实际发电功率的预测结果分析来验证该组合模型可行性和优越性。

1 理论与方法

1.1 变分模态分解

变分模态分解是一种时频分析方法,其能够自适应分解非平稳信号,将原始多分量信号分解为多个调幅调频单分量信号,有效避免了在迭代的过程中遇到的端点效应等问题。

VMD分解的每个模态uk(t)具有不同的有限带宽,而VMD的目标是使其分解的各子模态的估计带宽的和最小,其变分模型表达式为

(1)

为了求解式(1),先构建一个的增广拉格朗日函数,即

(2)

式(2)中:α>0;λ为乘法算子。

(3)

再更新中心频率,方法为

(4)

最后更新λ(t)的傅里叶变换,即

(5)

式(5)中:τ为步长,τ>0。

VMD分解的具体流程如表1所示。

表1 VMD具体流程Table 1 VMD-specific process

1.2 北方苍鹰优化算法

北方苍鹰优化算法(northern goshawk optimiz-ation, NGO)是一种群体的优化算法,该算法模拟了北方苍鹰捕杀猎物时的行为,具有卓越的优化性能,其寻优准确度及稳定性[22]。其规则如下。

步骤1初始化种群。种群成员在搜索空间中随机初始化。在北方苍鹰优化算法中,北方苍鹰种群用种群矩阵X为

(6)

式(6)中:Xi为第i个北方苍鹰的位置;N为北方苍鹰的种群数量;m为求解的维度;xi,j为第i个北方苍鹰的第j维的位置。

进行北方苍鹰优化算法时,北方苍鹰种群的目标函数值可以用向量表示,即

(7)

式(7)中:F为北方苍鹰种群的目标函数向量;Fi为第i个北方苍鹰的目标函数值。

步骤2猎物的识别和攻击。猎物识别是北方苍鹰在狩猎的第一阶段,北方苍鹰随机选择一个猎物,然后快速攻击它。此阶段为搜索空间的全局搜索,目的是识别最优区域。数学模型为

Pi=Xk,i=1,2,…,N,k=1,2,…,i-1,

i+1,…,N

(8)

(9)

(10)

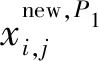
步骤3追逐和逃生。北方苍鹰攻击猎物后,猎物会试图逃跑,北方苍鹰需要继续追逐猎物。北方苍鹰的速度很快,所以它们几乎可以在任何情况下追逐猎物并最终捕获猎物。这种行为的模拟增加了算法对搜索空间的局部搜索的利用能力。在北方苍鹰优化算法中,假设这次狩猎范围的半径约为R。北方苍鹰与猎物之间的追逐过程的数学模型为

(11)

(12)

(13)

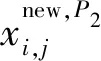
表2 NGO具体流程Table 2 NGO-specific process

1.3 K-means算法

K-means算法是最为常用的一种经典的聚类算法[23],基于数据之间的距离将相似特征的样本自动归到一个类别中,具有执行过程简单、收敛速度快的优点。K-means算法的基本过程如下。

步骤1随机选取K个点作为初始聚类的簇心。

步骤2分别计算其他每个样本点到K个簇心的欧式距离,将其余所有样本点归属到离该点最近的簇。

步骤3将所有样本点都归属到对应的K个簇后,更新簇心。

步骤4反复迭代步骤2～步骤3,直至簇心不再发生明显的变化,即收敛。

1.4 长短期记忆网络(LSTM)

长短期记忆网络(long short-term memory,LSTM)是为解决传统循环神经网络(RNN)在信息传递时出现的梯度消失、爆炸等问题而提出的一种改进RNN神经网络,其用记忆单元代替RNN的隐含节点,能够有效可靠地处理长时间序列数据。

LSTM的核心是它的“细胞状态”以及“门”结构。细胞状态是信息传输的路径,相当于网络的“记忆”;“门”结构的功能是实现信息的添加和丢弃。LSTM由多个重复的记忆块结构组成,每个记忆块结构都包含3个“门”结构,分别是遗忘门、输入门及输出门。LSTM利用激活函数σ来控制其3个“门”结构。单个LSTM的结构示意图如图1所示。

图1 LSTM结构示意图Fig.1 Schematic diagram of LSTM structure

LSTM3个“门”变量运算公式如下。

(1)遗忘门层ft由sigmoid层决定信息的更新。

ft=σ(Wf[ht-1,xt]+bf)

(14)

(15)

(3)输出门层有选择性地输出细胞状态信息。

(16)

式中:xt为细胞输入值;σ为sigmoid激活函数;Wf、Wi、WC、Wo分别为遗忘门、输入门、细胞状态、输出门sigmoid 激活函数的权重;bf、bi、bC、bo分别为遗忘门、输入门、细胞状态、输出门sigmoid 激活函数偏置;ht为时刻t的隐藏层向量。

2 风电功率预测模型的构建

2.1 基于NGO优化VMD

VMD可将原始风电功率分解成不同频率、具有较强规律性的风功率子序列,降低了风电功率序列的复杂度,但VMD必须需要预先人工设置其参数,在一定程度上影响了VMD分解的精度和效果,具有一定局限性。由于VMD分解效果与参数惩罚因子α和分解层数K密切相关,故本文采用北方苍鹰优化算法(NGO)对VMD的分解层数K和惩罚因子α进行寻优,将局部最小包络熵作为参数寻优的适应度函数。

包络熵可以反映原始风电信号的稀疏特性,当分解的子分量中包含较多的特征信息且噪声较少时,则包络熵值较小,反之,则包络熵值较大。包络熵Ep运算公式为

(17)

式(17)中:ej为a(j)归一化得到的结果;a(j)为VMD分解的K个子分量经过希尔伯特解调后的包络信号。

NGO-VMD算法的流图如图2所示。

2.2 基于K-means算法的数据重构

为了解决VMD分解出的模态分量个数过多,计算量繁冗的问题,通常需要对模态分量进行重构,已有文献大多将熵值相似的分量分为一类完成重构,如使用样本熵、排列熵[24]等。但使用熵值相似度进行各模态分量的重构的方法并为考虑到各模态分量数据本身的相似性,存在一定缺陷,因此本文研究中使用K-means算法完成对模态分量的重构。

K-means聚类算法基于数据之间的距离将相似特征的样本自动归到一个类别中,具有执行过程简单、收敛速度快的优点,但其需要人工确定聚类个数,具有一定局限性,为了更加合理地从不同角度地确定K-means的聚类个数,使用轮廓系数法与Davies-Boundin(DB)值对各聚类个数进行得分评价。

轮廓系数s越接近1表示该聚类效果越好,其计算公式为

(18)

图2 NGO-VMD算法流程Fig.2 Flow of NGO-VMD algorithm

式(18)中:disMeanout为该点与样本中非本类点的平均距离;disMeanin为该点与样本中本类点的平均距离。

DB值越小表示该分类效果越好。其计算公式为

(19)

式(19)中:K为分类数目;Si与Sj分别为样本i和样本j的类内平均距离;Mij为i类与j类中心的距离。

2.3 风电功率预测模型构建

为了解决在风电功率预测领域VMD人工设置难度大、分解效果差、分解模态分量个数多,计算量繁冗,以及未深度挖掘VMD残差项所包含的丰富信息导致超短期风功率预测精度受限的问题,提出了一种基于NGO-VMD二次分解其残差项、K-means重构与长短期记忆网络相结合的组合预测模型以提升超短期风电功率预测精度。具体流程如图3所示。

图3 组合预测模型流程Fig.3 Combined predictive model process

2.4 预测模型结果评价指标

为进一步验证模型预测性能及其有效性,选用均方根误差(RMSE)、平均绝对百分误差(MAPE)、平均绝对误差(MAE)、决定系数(R)对模型预测结果进行对比评估,其运算公式为

(20)

(21)

(22)

(23)

3 算例分析

通过对新疆某风电场的2019年实测风电功率数据的预测分析和比较来验证该组合模型的有效性和优越性。研究对象为6月1日—7月1日的实际风电功率数据,同时采样了风速、风向、温度、气压、湿度等数据,采样的间隔为15 min,即每日采样96个采样点。将6月1—30日的2 880个数据集作为模型的训练集,将7月1日的96个数据集作为测试集。

3.1 NGO-VMD分解

采用2.1节方法对VMD的分解层数K和惩罚因子α进行寻优。设置北方苍鹰种群数为20、最大迭代次数为30;设置分解层数K的寻优范围为[3,15],惩罚因子α的寻优范围为[100,3 000]。VMD其他参数均取默认值。经过北方苍鹰优化算法寻优的VMD最优参数组合[K,α]为[8,2 700]。NGO-VMD分解如图4所示,最后一个分量为残差项R,其大小为原始风电数据减去NGO-VMD分解的8个分量。

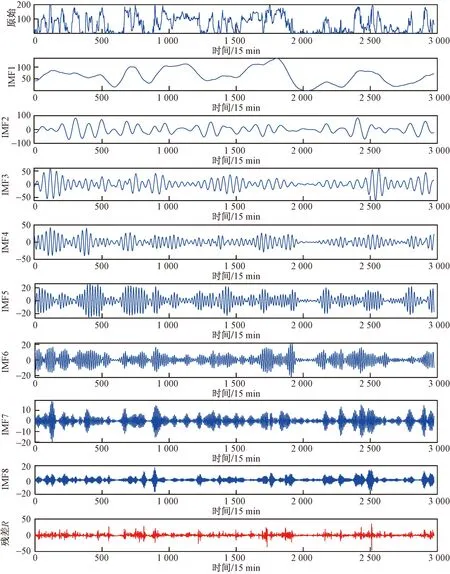
图4 NGO-VMD分解结果Fig.4 NGO-VMD decomposition results

将NGO-VMD分解的残差项R进行二次VMD分解,使用北方苍鹰优化算法对残差项R二次VMD分解的参数再次进行寻优,得到其最优参数组合[K1,α1]为[6,2 300]。NGO-VMD二次分解R如图5所示,最后一个分量为残差项R1,其大小为残差项R减去NGO-VMD二次分解的6个分量。

图5 NGO-VMD二次分解结果Fig.5 NGO-VMD quadratic decomposition results

3.2 K-means数据重构

使用轮廓系数法与Davies-Boundin(DB)值将原始风电数据NGO-VMD分解后的8个分量以及残差项R二次分解后的6个分量进行聚类数目得分评价,以确定各分量最佳重构个数。轮廓系数越接近1表示该聚类数目效果越好。DB值越小表示该聚类数目效果越好。

对首次原始风电数据NGO-VMD分解的8个分量进行K-means聚类,其聚类数目设置范围为[2,7]。由图6可知其IMF最佳聚类数目K为4,此时轮廓系数值最接近1,为0.935 9;DB值最小,为0.160 5。

图6 首次NGO-VMD分解聚类个数Fig.6 Number of first NGO-VMD decomposition clusters

对残差项R二次NGO-VMD分解的6个分量进行K-means聚类,其聚类数目设置范围为[2,5]。由图7可知其IMF最佳聚类数目K为3,此时轮廓系数值最接近1,为0.715 6;DB值最小,为0.423 8。

图7 二次NGO-VMD分解聚类个数Fig.7 Number of quadratic NGO-VMD decomposition clusters

3.3 风电功率模型预测结果

LSTM输入变量维数为6,包括风电功率、风速、风向、温度、气压、湿度;输出变量维数为1,为风电功率。将LSTM的迭代次数设为100次,初始学习率为0.005。由于Adam算法能计算不同参数下的学习率且运算速度快、内存小,因此本文研究中LSTM求解器选择为Adam。随着LSTM隐藏层数的增加,虽然预测模型的拟合能力会进一步得到改善,但如果不加限制,会出现模型预测时间过长、过拟合等问题,因此本文设置LSTM隐藏层数为两层,层数分别为100、50,为了避免出现过拟合现象,给LSTM每一层加入元素失活概率为20%的随机失活(Dropout)层。

将NGO-VMD二次分解R-Kmeans-LSTM模型各部分的参数确定好后,用该模型预测首次及二次分解后重构后的各子模态分量,并叠加各子模态分量的预测结果作为超短期风功率预测的最终结果。为了验证本文模型的有效性,构建LSTM、未经二次分解的NGO-VMD-LSTM、子模态未重构的NGO-VMD二次分解R-LSTM 等模型与本文方法做对比,试验结果如图8及表3所示。